Geometrischer Mittelwert: Eine Maßnahme für Wachstum und Compounding

Hast du schon einmal den Durchschnitt deiner jährlichen Rendite berechnet und dann festgestellt, dass deine tatsächliche Gesamtrendite nicht ganz so hoch ist? Dieses häufige Szenario in der Finanzwelt zeigt, wie wichtig es ist, das geometrische Mittel zu verstehen und anzuwenden - ein nützliches Maß, das sich oft als besser geeignet erweist als das weit verbreitete arithmetische Mittel, wenn es um Änderungsraten und Aufzinsungseffekte geht.

In diesem Tutorium werden wir das Konzept des geometrischen Mittels und seine Rolle in der Datenanalyse untersuchen, insbesondere in Bereichen wie Finanzen, Biologie und Datenwissenschaft. Wir werden auch Szenarien untersuchen, in denen er andere Maße der zentralen Tendenz übertrifft.

Was ist das Geometrische Mittel?

Das geometrische Mittel ist eine Art Durchschnitt, der besonders nützlich ist, wenn du mit Mengen positiver Zahlen arbeitest, vor allem wenn es um Multiplikation oder exponentielles Wachstum geht. Im Gegensatz zum arithmetischen Mittel, bei dem Zahlen addiert und durch die Anzahl geteilt werden, eignet sich das geometrische Mittel besonders gut für Datensätze mit multiplikativen Beziehungen oder exponentiellem Wachstum.

Hier sind einige der Bereiche, in denen das geometrische Mittel wertvoll ist:

1. Finanzen: Sie wird häufig verwendet, um die durchschnittliche Rendite über mehrere Zeiträume zu berechnen. Im Gegensatz zum arithmetischen Mittel berücksichtigt das geometrische Mittel den Zinseszinseffekt, was es für finanzielle Berechnungen genauer macht.
2. Biologie: In Studien zum Bevölkerungswachstum wird das geometrische Mittel verwendet, um die durchschnittlichen Wachstumsraten im Laufe der Zeit zu berechnen.
3. Geometrie: Eine seiner elegantesten Erscheinungsformen ist das rechtwinklige Dreieck, bei dem die Höhe der Hypotenuse das geometrische Mittel der Segmente verkörpert, die sie auf der Hypotenuse bildet. Das geometrische Mittel gibt außerdem die Seitenlänge eines Quadrats an, das die gleiche Fläche wie ein bestimmtes Rechteck hat, und ermöglicht es, rechteckige Flächen zu "quadrieren".

Wie du siehst, ist das geometrische Mittel sowohl bei alltäglichen Berechnungen als auch bei abstrakteren mathematischen Konzepten ein wertvolles Werkzeug.

So berechnest du das geometrische Mittel

Es gibt verschiedene Methoden zur Berechnung des geometrischen Mittels, die je nach Situation ihre eigenen Vorteile haben.

Die Formel für das geometrische Mittel

Die einfachste Art, das geometrische Mittel zu berechnen, ist die Verwendung der Standardformel: 

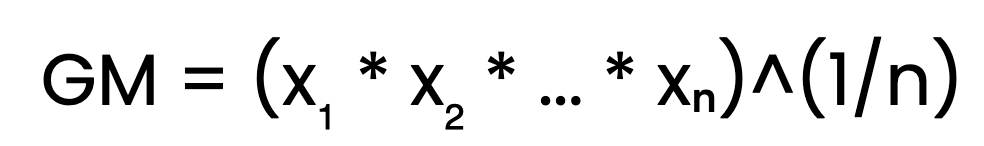
Dabei sind x₁, x₂, ..., xₙ die positiven Zahlen im Datensatz, und n ist die Anzahl der Zahlen. Um das geometrische Mittel zu erhalten, multiplizieren wir alle Werte miteinander und ziehen die n-te Wurzel aus dem Produkt, wobei n die Anzahl der Werte ist. Lass uns das anhand eines Beispiels verdeutlichen. Betrachte die Zahlen 2, 4 und 8. Um ihr geometrisches Mittel zu finden:

1. Multipliziere die Zahlen: 2 * 4 * 8 = 64
2. Ziehe die Kubikwurzel (da es 3 Zahlen gibt): ∛64 ≈ 4

Das geometrische Mittel aus 2, 4 und 8 ist 4. Dieses Ergebnis sagt uns, dass, wenn wir drei gleiche Zahlen hätten, die jeweils gleich 4 sind, ihr Produkt dasselbe wäre wie das Produkt der ursprünglichen Zahlen. Im Wesentlichen ist 4 der einheitliche Wachstumsfaktor für alle drei Werte.

Berechnung des geometrischen Mittels durch Addition der Logarithmen

Für größere Datensätze oder um Überlauffehler bei sehr großen Zahlen zu vermeiden, können wir Logarithmen verwenden. Diese Methode vereinfacht die Multiplikation zur Addition und macht die Berechnungen überschaubarer. Hier nehmen wir zuerst den Logarithmus jeder Zahl, berechnen das arithmetische Mittel dieser Logarithmen und nehmen dann den Antilog (Exponentialwert) dieses Mittels. Nehmen wir das gleiche Beispiel wie oben. 

1. Nimm Logarithmen (Basis 10): log(2) ≈ 0,3010, log(4) ≈ 0,6021, log(8) ≈ 0,9031
2. Berechne das arithmetische Mittel: (0.3010 + 0.6021 + 0.9031) / 3 ≈ 0.6021
3. Nimm den Antilog: (10^x) = 10^0.6021 ≈ 4

Diese Methode liefert das gleiche Ergebnis wie die direkte Berechnungsmethode. Du kannst Logarithmen mit beliebiger Basis verwenden (z. B. natürliche Logarithmen mit der Basis e), solange du während der gesamten Berechnung dieselbe Basis verwendest. Der endgültige geometrische Mittelwert wird derselbe sein.

Geometrisches Mittel in Datenwissenschaft und maschinellem Lernen

Das geometrische Mittel ist ein nützliches statistisches Maß mit mehreren wichtigen Anwendungen in der Datenwissenschaft und im maschinellen Lernen. Hier sind drei wichtige Anwendungsfälle, in denen sich das geometrische Mittel bewährt. 

Wachstumsraten und Zeitreihenanalyse

In der Datenwissenschaft analysieren wir oft Wachstumsraten im Laufe der Zeit, z. B. bei der Bevölkerungsdynamik, bei Markttrends oder bei der Nutzerakzeptanzrate. Das geometrische Mittel ist für diese Situationen ideal, weil es den Aufzinsungseffekt des Wachstums genau abbildet. Im Gegensatz zum arithmetischen Mittel, bei dem die Raten einfach gemittelt werden, ohne zu berücksichtigen, wie das Wachstum jedes Jahres auf dem des letzten aufbaut, berücksichtigt das geometrische Mittel diesen Aufzinsungseffekt.

Stell dir vor, du analysierst die jährliche Wachstumsrate der Nutzerbasis eines Start-ups über fünf Jahre: 20%, 15%, 25%, 10% und 30%. Das arithmetische Mittel (20 %) scheint zwar eine schnelle Lösung zu sein, berücksichtigt aber nicht den Aufzinsungseffekt. Das geometrische Mittel ((1,20 * 1,15 * 1,25 * 1,10 * 1,30)^(1/5) - 1 ≈ 19,77%) liefert eine genauere durchschnittliche Wachstumsrate, die bei konsequenter Anwendung jedes Jahr zum gleichen Endwert wie die tatsächlichen unterschiedlichen Wachstumsraten führen würde.

Statistische Analyse von schiefen Daten

In der Datenwissenschaft haben wir es oft mit Datensätzen zu tun, die aufgrund multiplikativer Prozesse positiv verzerrt sind, z. B. Einkommensverhältnisse, biologische Messungen oder bestimmte Finanzindikatoren. In solchen Fällen kann die Verwendung des arithmetischen Mittels irreführend sein, weil es empfindlich auf Extremwerte (Ausreißer) reagiert, die die Darstellung der zentralen Tendenz verzerren können.

Das geometrische Mittel ist besonders nützlich, wenn du mit Daten arbeitest, die einer Log-Normal-Verteilung folgen. Hier ist der Grund dafür:

• Minimiert den Einfluss von Ausreißern: Der geometrische Mittelwert reduziert die Auswirkungen extrem hoher oder niedriger Werte und bietet einen repräsentativeren zentralen Wert für schiefe Daten.
• Behandelt multiplikative Beziehungen: Sie ist für Daten geeignet, bei denen die Werte nicht additiv, sondern multiplikativ kombiniert werden.

Nehmen wir einen Datensatz über die Haushaltseinkommen in einer Region, in der die meisten Haushalte zwischen 30.000 und 60.000 Dollar verdienen, aber einige wenige über 1 Million Dollar.

• Arithmetisches Mittel des Einkommens: Dieser Wert wird stark von den Ausreißern mit hohem Einkommen beeinflusst, was auf ein Durchschnittseinkommen schließen lässt, das viel höher ist als das, was die meisten Menschen verdienen.
• Geometrischer Mittelwert des Einkommens: So erhält man einen zentralen Wert, der das typische Einkommen genauer widerspiegelt, indem der Einfluss der Extremwerte minimiert wird.

Durch die Verwendung des geometrischen Mittels können Datenwissenschaftler in solchen Fällen ein genaueres Maß für die zentrale Tendenz erhalten, was zu besseren Erkenntnissen und zuverlässigeren Analysen führt. Das macht das geometrische Mittel zu einem unverzichtbaren Werkzeug bei der Arbeit mit schiefen Datenverteilungen in verschiedenen Bereichen.

Bewertungsmetriken für unausgewogene Datensätze

Bei Klassifizierungsaufgaben stoßen wir oft auf unausgewogene Datensätze, bei denen einige Gruppen durch eine viel größere Anzahl von Beispielen vertreten sind als andere. In solchen Fällen können traditionelle Bewertungsmaßstäbe wie die Genauigkeit irreführend sein. An dieser Stelle wird der Geometrische Mittelwert (G-Mittelwert) zu einem wertvollen Instrument.

Der G-Mittelwert ist die Wurzel aus dem Produkt der klassenweisen Sensitivität (Recall). Bei einer binären Klassifizierung ist es die Quadratwurzel aus dem Produkt von Sensitivität und Spezifität. Bei Mehrklassenproblemen ist es die höhere Wurzel aus dem Produkt der Sensitivitäten der einzelnen Klassen.

G-Mean zielt darauf ab, die Genauigkeit über alle Klassen hinweg auszugleichen, was es besonders nützlich für unausgewogene Datensätze macht. Es ist jedoch wichtig zu wissen, dass G-Mean undefiniert ist, wenn eine Klasse eine Sensitivität von Null hat, was seine Anwendbarkeit in extremen Ungleichgewichtsszenarien einschränkt. In der Praxis können modifizierte Versionen oder alternative Messgrößen verwendet werden, um diese Einschränkung zu umgehen.

Wenn du mehr darüber erfahren möchtest, wie das geometrische Mittel und andere statistische Maße beim maschinellen Lernen angewendet werden, solltest du unseren Karrierepfad "Machine Learning Scientist with Python " in Erwägung ziehen. Dieser bietet vertiefenden Unterricht, der die wichtigsten Konzepte und Techniken des maschinellen Lernens mit praktischen Einblicken und praktischer Erfahrung abdeckt.