Média geométrica: Uma medida para crescimento e composição

Você já calculou a média dos retornos anuais de seus investimentos e descobriu que o retorno geral real não corresponde exatamente à média? Esse cenário comum em finanças destaca a importância de compreender e aplicar a média geométrica - uma medida útil que muitas vezes se mostra mais apropriada do que a média aritmética amplamente utilizada ao lidar com taxas de alteração e efeitos compostos.

Neste tutorial, exploraremos o conceito de média geométrica e sua função na análise de dados, especialmente em áreas como finanças, biologia e ciência de dados. Também examinaremos cenários em que ela supera outras medidas de tendência central.

O que é a média geométrica?

A média geométrica é um tipo de média que é particularmente útil quando você trabalha com conjuntos de números positivos, especialmente aqueles que envolvem multiplicação ou crescimento exponencial. Diferentemente da média aritmética mais comum, que adiciona números e divide pela contagem, a média geométrica é particularmente adequada para lidar com conjuntos de dados que envolvem relações multiplicativas ou crescimento exponencial.

Aqui estão alguns dos campos em que a média geométrica é valiosa:

1. Finanças: É comumente usado para calcular taxas médias de retorno em vários períodos. Ao contrário da média aritmética, a média geométrica leva em conta a composição, o que a torna mais precisa para cálculos financeiros.
2. Biologia: Nos estudos de crescimento populacional, a média geométrica é usada para calcular as taxas médias de crescimento ao longo do tempo.
3. Geometria: Uma de suas aparições mais elegantes é em triângulos retângulos, onde a altitude da hipotenusa incorpora a média geométrica dos segmentos que ela cria nessa hipotenusa. Além disso, a média geométrica representa o comprimento do lado de um quadrado que teria a mesma área de um determinado retângulo, fornecendo uma maneira de "quadrar" áreas retangulares.

Como você pode ver, a média geométrica é uma ferramenta valiosa tanto para cálculos cotidianos quanto para conceitos matemáticos mais abstratos.

Como calcular a média geométrica

Há vários métodos para calcular a média geométrica, cada um com suas próprias vantagens, dependendo da situação.

A fórmula da média geométrica

A maneira mais direta de calcular a média geométrica é usar a fórmula padrão: 

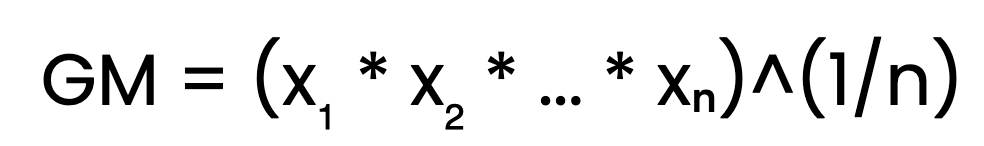
Aqui, x₁, x₂, ..., xₙ são os números positivos no conjunto de dados e n é a contagem de números. Para obter a média geométrica, multiplicamos todos os valores e tiramos a enésima raiz do produto, em que n é o número de valores. Vamos mostrar isso por meio de um exemplo. Considere os números 2, 4 e 8. Para encontrar sua média geométrica:

1. Multiplique os números: 2 * 4 * 8 = 64
2. Pegue a raiz cúbica (já que há 3 números): ∛64 ≈ 4

A média geométrica de 2, 4 e 8 é 4. Esse resultado nos diz que, se tivéssemos três números iguais, cada um igual a 4, o produto deles seria o mesmo que o produto dos números originais. Essencialmente, 4 é o fator de crescimento consistente em todos os três valores.

Cálculo da média geométrica pela adição de logaritmos

Para conjuntos de dados maiores ou para evitar erros de estouro ao lidar com números muito grandes, podemos usar logaritmos. Esse método simplifica a multiplicação em adição e torna os cálculos mais fáceis de gerenciar. Aqui, primeiro pegamos o logaritmo de cada número, calculamos a média aritmética desses logaritmos e, em seguida, pegamos o antilogaritmo (exponencial) dessa média. Vamos usar o mesmo exemplo acima. 

1. Use logaritmos (base 10): log(2) ≈ 0,3010, log(4) ≈ 0,6021, log(8) ≈ 0,9031
2. Calcule a média aritmética: (0.3010 + 0.6021 + 0.9031) / 3 ≈ 0.6021
3. Pegue o antilog: (10^x) = 10^0.6021 ≈ 4

Esse método nos dá o mesmo resultado que o método de cálculo direto. Você pode usar logaritmos de qualquer base (como logaritmos naturais com base e), desde que use a mesma base em todo o cálculo. A média geométrica final será a mesma.

Média geométrica em ciência de dados e aprendizado de máquina

A média geométrica é uma medida estatística útil com várias aplicações importantes em ciência de dados e aprendizado de máquina. Aqui estão três casos de uso importantes em que a média geométrica se mostra valiosa. 

Taxas de crescimento e análise de séries temporais

Na ciência de dados, geralmente analisamos as taxas de crescimento ao longo do tempo, como na dinâmica populacional, nas tendências de mercado ou nas taxas de adoção de usuários. A média geométrica é ideal para essas situações porque captura com precisão a natureza composta do crescimento. Ao contrário da média aritmética, que simplesmente calcula a média das taxas sem considerar como o crescimento de cada ano se baseia no último, a média geométrica leva em conta esse efeito de composição.

Imagine que você está analisando a taxa de crescimento anual da base de usuários de uma startup ao longo de cinco anos: 20%, 15%, 25%, 10% e 30%. Embora a média aritmética (20%) possa parecer uma solução rápida, ela não leva em conta o efeito de composição. A média geométrica ((1,20 * 1,15 * 1,25 * 1,10 * 1,30)^(1/5) - 1 ≈ 19,77%) fornece uma taxa de crescimento média mais precisa que, se aplicada consistentemente a cada ano, resultaria no mesmo valor final que as taxas de crescimento variadas reais.

Análise estatística de dados enviesados

Na ciência de dados, geralmente lidamos com conjuntos de dados que são positivamente distorcidos devido a processos multiplicativos, como níveis de renda, medições biológicas ou determinados indicadores financeiros. Nesses casos, o uso da média aritmética pode ser enganoso, pois ela é sensível a valores extremos (outliers), que podem distorcer a representação da tendência central.

A média geométrica é particularmente útil ao lidar com dados que seguem uma distribuição log-normal. Aqui está o motivo:

• Minimiza a influência de valores discrepantes: A média geométrica reduz o impacto de valores extremamente altos ou baixos, fornecendo um valor central mais representativo para dados distorcidos.
• Lida com relacionamentos multiplicativos: É apropriado para dados em que os valores são combinados de forma multiplicativa em vez de aditiva.

Considere um conjunto de dados de renda familiar em uma região onde a maioria das famílias ganha entre US$ 30.000 e US$ 60.000, mas algumas ganham mais de US$ 1 milhão.

• Renda média aritmética: Isso será muito influenciado pelos valores atípicos de alta renda, o que pode sugerir uma renda média muito maior do que a que a maioria das pessoas ganha.
• Renda média geométrica: Isso fornece um valor central que reflete a renda típica com mais precisão, minimizando a influência dos valores extremos.

Ao usar a média geométrica nesses casos, os cientistas de dados podem obter uma medida mais precisa da tendência central, o que leva a melhores percepções e análises mais confiáveis. Isso faz com que a média geométrica seja uma ferramenta essencial ao trabalhar com distribuições de dados distorcidas em vários campos.

Métricas de avaliação para conjuntos de dados desequilibrados

Em tarefas de classificação, frequentemente encontramos conjuntos de dados desequilibrados, nos quais alguns grupos são representados por um número muito maior de exemplos do que outros. Nesses casos, as métricas de avaliação tradicionais, como a precisão, podem ser enganosas. É nesse ponto que a pontuação média geométrica, ou média G, torna-se uma ferramenta valiosa.

O G-Mean é a raiz do produto da sensibilidade por classe (recall). Para classificação binária, é a raiz quadrada do produto da sensibilidade e da especificidade. Para problemas de várias classes, é uma raiz superior do produto da sensibilidade de cada classe.

O G-Mean visa equilibrar a precisão em todas as classes, o que o torna particularmente útil para conjuntos de dados desequilibrados. No entanto, é importante observar que o G-Mean é indefinido quando qualquer classe tem sensibilidade zero, limitando sua aplicabilidade em cenários de desequilíbrio extremo. Na prática, versões modificadas ou métricas alternativas podem ser usadas para resolver essa limitação.

Para saber mais sobre como a média geométrica e outras medidas estatísticas são aplicadas no aprendizado de máquina, considere explorar nossa carreira de Cientista de Aprendizado de Máquina com Python, que oferece aulas aprofundadas que abrangem conceitos e técnicas essenciais de aprendizado de máquina, com insights práticos e experiência prática.