Tutoriel sur le regroupement K-Means dans R

Vue d'ensemble du regroupement k-Means

Les modèles de classification visent à regrouper les données en "clusters" ou groupes distincts. Il peut être utilisé comme analyse en soi ou comme caractéristique dans un algorithme d'apprentissage supervisé.

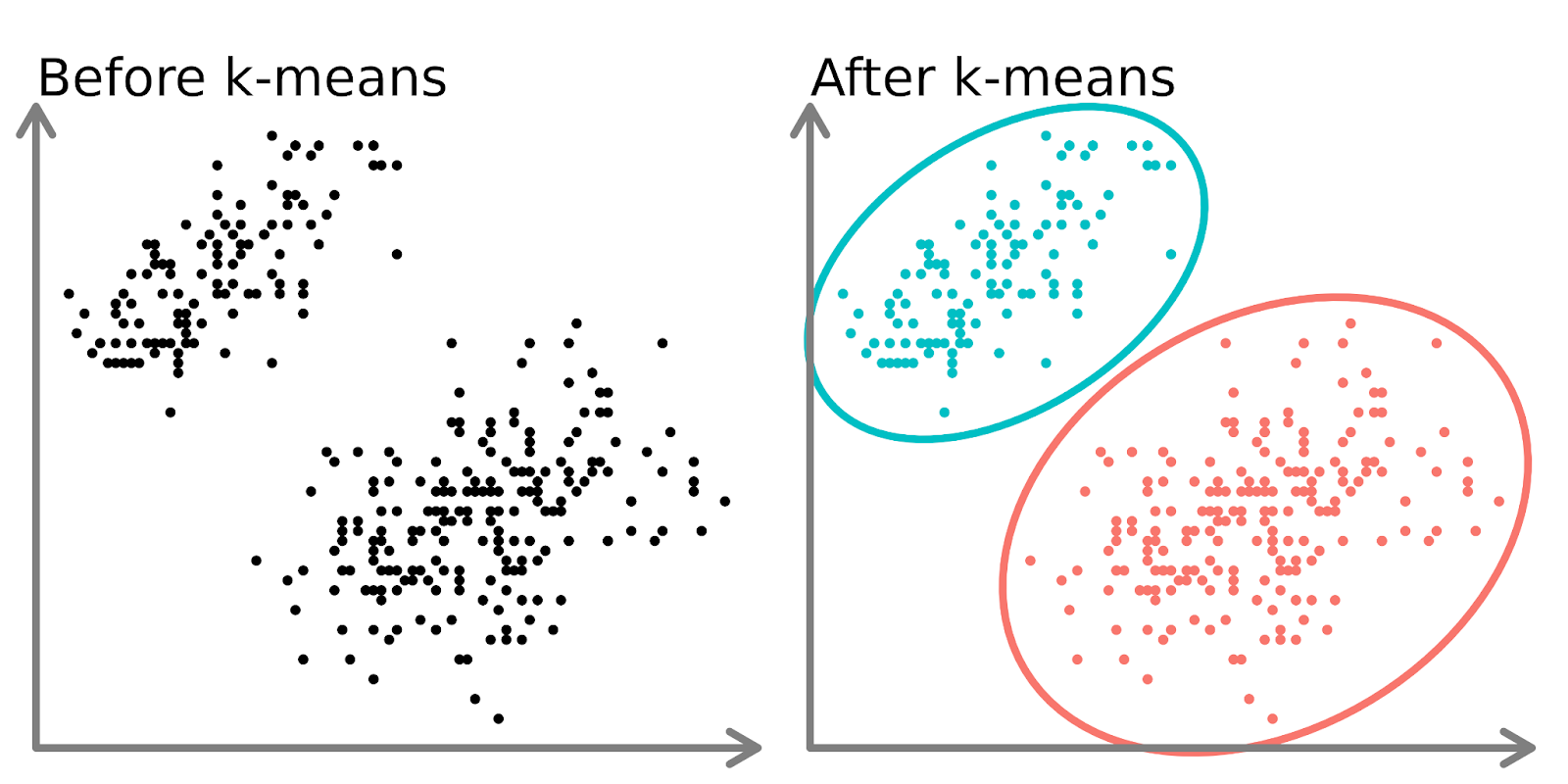
Dans la partie gauche du diagramme ci-dessus, nous pouvons voir deux ensembles distincts de points non étiquetés et colorés comme des points de données similaires. L'ajustement d'un modèle k-means à ces données (partie droite) permet de mettre en évidence deux groupes distincts (représentés par des cercles et des couleurs distincts). 

En deux dimensions, il est facile pour les humains de diviser ces groupes, mais avec plus de dimensions, vous devez utiliser un modèle.

L'algorithme k-means

Imaginez que vous souhaitiez créer plusieurs salades de fruits, chacune composée de fruits similaires.

1. Vous décidez du nombre de salades de fruits que vous souhaitez créer (k). Par exemple, vous décidez de préparer 3 salades de fruits.
2. Vous choisissez au hasard 3 fruits sur le tableau comme "représentants" de départ de chaque salade.
3. Faites ensuite un tour de table et attribuez chaque fruit à la salade dont il est le représentant le plus proche. Par exemple, les pommes peuvent aller avec les poires, les oranges avec les mandarines et les bananes avec les plantains.
4. Une fois que tous les fruits ont été attribués, vous trouvez le nouveau "centre" de chaque salade de fruits en calculant les caractéristiques moyennes des fruits dans chaque groupe (par exemple, la taille, la couleur, le goût). Ces nouveaux centres deviennent les représentants actualisés.
5. Vous répétez les étapes 3 et 4 plusieurs fois, en attribuant les fruits au représentant le plus similaire et en mettant à jour le représentant à chaque fois jusqu'à ce que les regroupements ne changent plus.

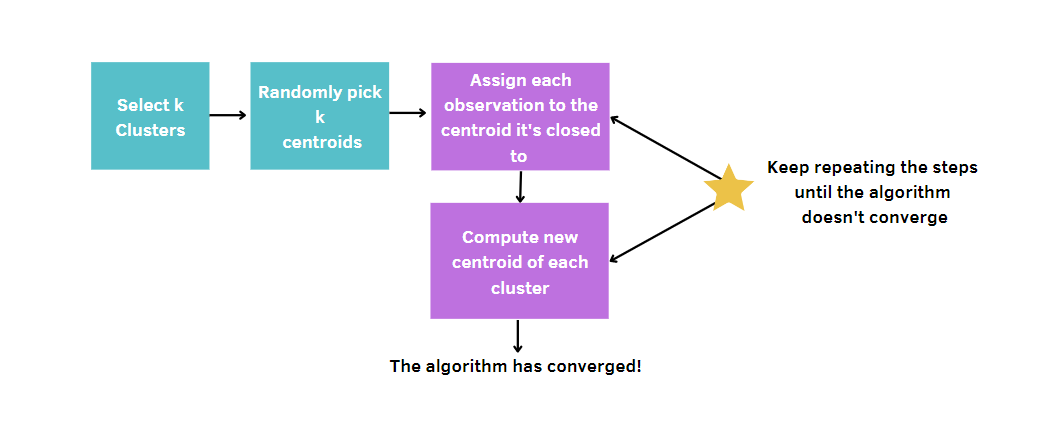
Plus généralement, vous :

1. Choisissez le nombre de grappes, k.
2. Sélectionnez k points (grappes de taille 1) au hasard.
3. Calculez la distance entre chaque point et le centroïde et affectez chaque point de données au groupe le plus proche.
4. Calculez le centroïde (position moyenne) pour chaque groupe.
5. Répétez les étapes 3-4 jusqu'à ce que les groupes ne changent plus ou que le nombre maximum d'itérations soit atteint.

Étant donné que les k-moyens choisissent aléatoirement les centres des grappes, cet algorithme doit être exécuté un certain nombre de fois, fixé par l'utilisateur. De cette manière, la meilleure solution sera atteinte en minimisant la mesure de la qualité d'un modèle. Cette mesure s'appelle la somme totale des carrés à l'intérieur d'un groupe (WCSS), c'est-à-dire la somme des distances entre les points de données et le centroïde correspondant pour chaque groupe. En effet, plus la mesure de la qualité de notre modèle est petite, plus nous atteindrons le modèle gagnant.

Ensemble de données sur les annonces Airbnb

Tout le contenu de ce tutoriel tournera autour des annonces de location Airbnb au Cap, disponibles sur DataLab. Les données contiennent différents types d'informations, comme les hôtes, le prix, le nombre d'avis, les coordonnées, etc. 

Même si l'ensemble des données semble fournir des informations approfondies sur les locations de vacances, il reste encore quelques questions claires auxquelles il est possible de répondre. Imaginons par exemple qu'Airbnb demande à ses data scientists d'étudier la segmentation des annonces sur cette plateforme au Cap. 

Chaque ville est différente des autres et a des exigences différentes en fonction de la culture des personnes qui y vivent. L'identification de grappes dans cette ville peut être utile pour extraire de nouvelles informations susceptibles d'accroître la satisfaction des clients actuels grâce à des stratégies de fidélisation de la clientèle adaptées, évitant ainsi le départ de ces derniers. Dans le même temps, il est également essentiel d'attirer de nouvelles personnes grâce à des promotions appropriées. 

Visualisez les données d'Airbnb

Avant d'appliquer les k-means, nous aimerions étudier plus en détail la relation entre les variables en examinant la matrice de corrélation. Pour des raisons de commodité d'affichage, nous arrondissons les chiffres à deux décimales.

library(dplyr)
airbnb |>
  select(price, minimum_nights, number_of_reviews) |>
  cor(use = "pairwise.complete.obs") |>
  round(2)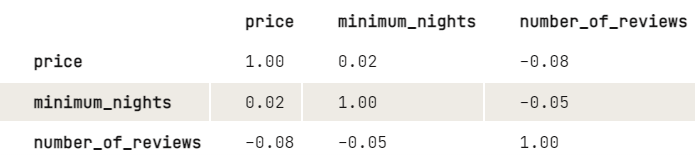

D'après les résultats, il semble y avoir une légère relation négative entre le prix et le nombre d'avis : Plus le prix est élevé, plus le nombre de commentaires est faible. Il en va de même pour les nuits minimales et un certain nombre de commentaires. Étant donné que le nombre minimum de nuits n'a pas une grande incidence sur le prix, nous aimerions simplement étudier davantage le lien entre le prix et le nombre d'avis :

library(ggplot2)
ggplot(data, aes(number_of_reviews, price, color = room_type, shape = room_type)) +
    geom_point(alpha = 0.25) +
    xlab("Number of reviews") +
    ylab("Price")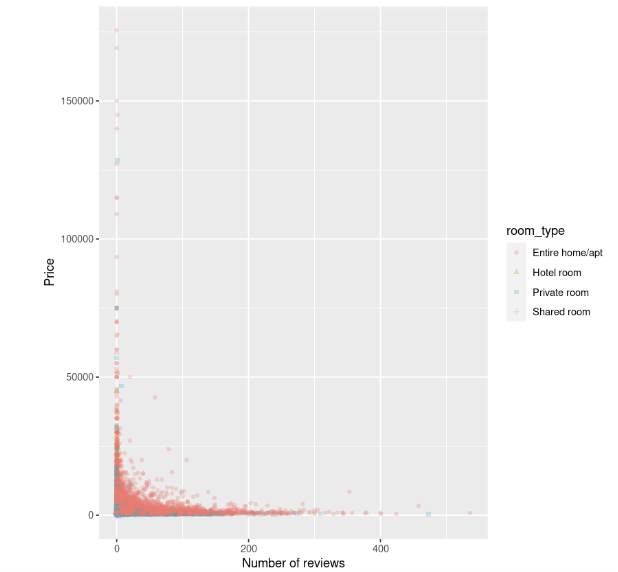

Le nuage de points montre que le coût des hébergements, en particulier des maisons entières, est plus élevé lorsque le nombre d'avis est faible et semble diminuer à mesure que le nombre d'avis augmente. 

Normalisation

Avant d'ajuster le modèle, il y a une autre étape à franchir. k-means est sensible aux variables qui ont des unités incomparables, ce qui conduit à des résultats trompeurs. Dans cet exemple, le nombre d'avis est de quelques dizaines ou centaines, mais le prix est de plusieurs dizaines de milliers. Sans traitement des données, les différences de prix sembleraient plus importantes que les différences de commentaires, mais nous voulons que ces variables soient traitées de la même manière.

Pour éviter ce problème, les variables doivent être transformées pour être sur une échelle similaire. Ils peuvent ainsi être comparés correctement à l'aide de la métrique de la distance.

Il existe différentes méthodes pour résoudre ce problème. La plus connue et la plus utilisée est la normalisation, qui consiste à soustraire la valeur moyenne de la valeur de la caractéristique et à la diviser par son écart-type. Cette technique permet d'obtenir des caractéristiques avec une moyenne de 0 et un écart de 1. 

Vous pouvez mettre les variables à l'échelle à l'aide de la fonction scale(). Puisque cette méthode renvoie une matrice, le code est plus propre en utilisant un style base-R plutôt qu'un style tidyverse.

airbnb[, c("price", "number_of_reviews")] = scale(airbnb[, c("price", "number_of_reviews")])

Ajustement et évaluation du modèle

Nous pouvons enfin identifier les groupes d'inscriptions à l'aide de la méthode des k-moyennes. Pour commencer, essayons d'effectuer des k-means en définissant 3 grappes et nstart égal à 20. Ce dernier paramètre est nécessaire pour exécuter k-means avec 20 affectations de départ aléatoires différentes et, ensuite, R choisira automatiquement les meilleurs résultats totaux de la somme des carrés à l'intérieur d'un cluster. Nous avons également défini une graine afin de reproduire les mêmes résultats à chaque fois que nous exécutons le code.

# Get the two columns of interest
airbnb_2cols <- data[, c("price", "number_of_reviews")]

set.seed(123)
km.out <- kmeans(airbnb_2cols, centers = 3, nstart = 20)
km.out

Sortie :

K-means clustering with 3 clusters of sizes 785, 37, 16069

Cluster means:
     price number_of_reviews
1 14264.102         5.9401274
2 83051.541         0.6756757
3  1589.879        18.2649200

Clustering vector:
   [1] 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
  [37] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
  [73] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
 [109] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 3 3 3 3 3
 [145] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 1 3 3
...
[16777] 3 3 3 3 3 3 3 3 3 3 1 3 3 1 3 1 3 3 3 3 3 1 3 3 3 3 3 3 3 3 1 3 3 3 3 3
[16813] 3 1 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 3
[16849] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 3 3 3
[16885] 3 3 3 3 3 3 3

Within cluster sum of squares by cluster:
[1] 41529148852 49002793251 33286433394
(between_SS / total_SS =  74.5 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"

Le résultat montre que trois groupes différents ont été trouvés avec des tailles de 785, 37 et 16069. Pour chaque groupe, les distances au carré entre les observations et les centroïdes sont calculées. Ainsi, chaque observation sera affectée à l'un des trois groupes. 

Même si le résultat semble bon, la meilleure façon de trouver le meilleur modèle est d'essayer différents modèles avec un nombre différent de grappes. Nous devons donc commencer par un modèle avec une seule grappe, puis essayer un modèle avec deux grappes, et ainsi de suite. Toute cette procédure doit être cursusée à l'aide d'une représentation graphique, appelée scree plot, dans laquelle le nombre de clusters est représenté sur l'axe des x, tandis que le WCSS est sur l'axe des y. 

Dans cette étude de cas, nous construisons 10 modèles k-means, chacun d'entre eux ayant un nombre différent de grappes, pour atteindre un maximum de 10 grappes. De plus, nous n'utiliserons qu'une partie de l'ensemble de données. Nous n'incluons donc que le prix et le nombre d'avis. Pour tracer le scree plot, nous devons enregistrer la somme totale des carrés à l'intérieur du cluster de tous les modèles dans la variable wss.

# Decide how many clusters to look at
n_clusters <- 10

# Initialize total within sum of squares error: wss
wss <- numeric(n_clusters)

set.seed(123)

# Look over 1 to n possible clusters
for (i in 1:n) {
  # Fit the model: km.out
  km.out <- kmeans(airbnb_2cols, centers = i, nstart = 20)
  # Save the within cluster sum of squares
  wss[i] <- km.out$tot.withinss
}

# Produce a scree plot
wss_df <- tibble(clusters = 1:n, wss = wss)
 
scree_plot <- ggplot(wss_df, aes(x = clusters, y = wss, group = 1)) +
    geom_point(size = 4)+
    geom_line() +
    scale_x_continuous(breaks = c(2, 4, 6, 8, 10)) +
    xlab('Number of clusters')
scree_plot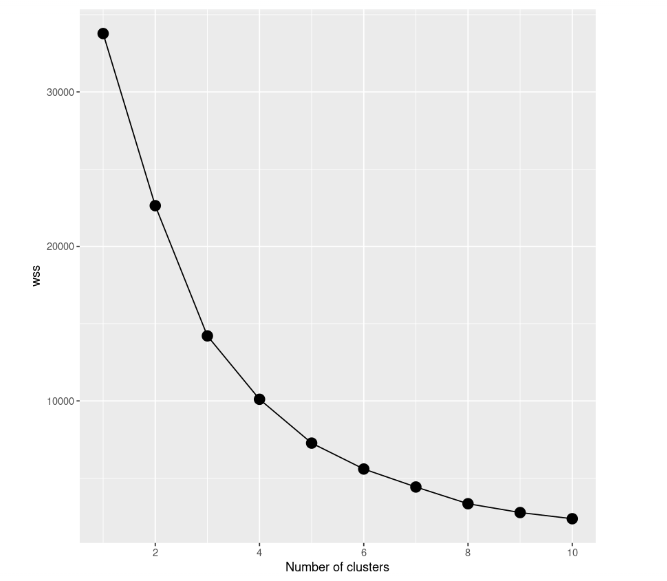

En examinant le scree plot, nous pouvons remarquer que la somme totale des carrés à l'intérieur des grappes diminue au fur et à mesure que le nombre de grappes augmente. Le critère de choix du nombre de grappes consiste à trouver un coude tel que vous puissiez trouver un point où le WCSS diminue beaucoup plus lentement après l'ajout d'une autre grappe. Dans ce cas, ce n'est pas très clair, nous allons donc ajouter des lignes horizontales pour avoir une meilleure idée :

scree_plot +
    geom_hline(
        yintercept = wss, 
        linetype = 'dashed', 
        col = c(rep('#000000',4),'#FF0000', rep('#000000', 5))
    )

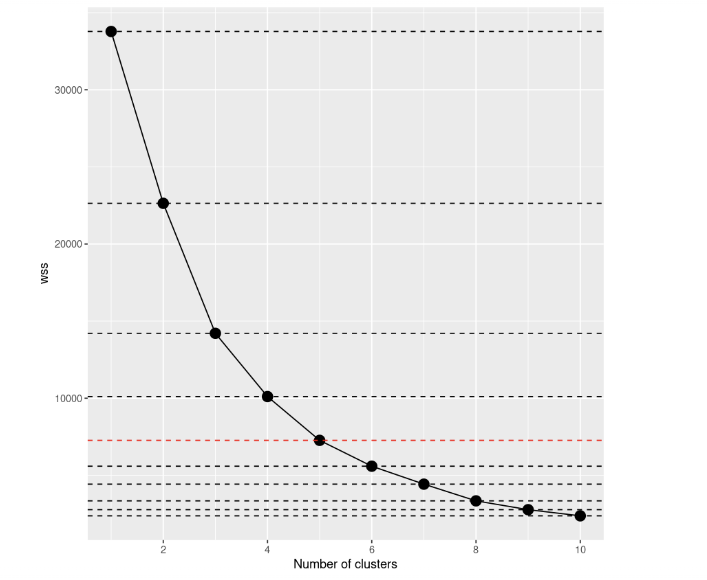
Si vous y regardez à nouveau, la décision à prendre semble beaucoup plus claire qu'auparavant, ne pensez-vous pas ? D'après cette visualisation, nous pouvons dire que le meilleur choix est d'établir un nombre de grappes égal à 5. Après k=5, les améliorations des modèles semblent se réduire fortement. 

# Select number of clusters
k <- 5
set.seed(123)
# Build model with k clusters: km.out
km.out <- kmeans(airbnb_2cols, centers = k, nstart = 20)

Nous pouvons essayer à nouveau de visualiser le nuage de points entre le prix et le nombre d'avis. Nous colorons également les points en fonction de l'identifiant de la grappe :

data$cluster_id <- factor(km.out$cluster)
ggplot(data, aes(number_of_reviews, price, color = cluster_id)) +
    geom_point(alpha = 0.25) +
    xlab("Number of reviews") +
    ylab("Price")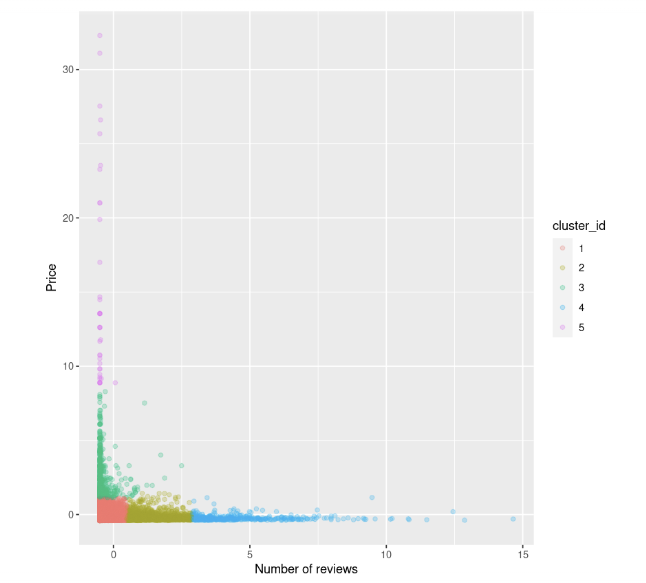

Nous pouvons l'observer :

• Il y a quelques annonces qui ont des prix élevés et peu d'avis, colorées en vert et en fuchsia.
• Nous disposons également d'un groupe de points de données comportant à la fois des prix bas et des avis, marqués en rouge.
• Ensuite, le prix semble se stabiliser dès que le nombre d'avis augmente.

Quand les K-Means échoueront-ils ?

Gardez à l'esprit que la méthode k-means est simple et facile à appliquer, mais qu'elle n'est pas toujours le meilleur choix pour segmenter les données en groupes, car elle peut échouer. L'algorithme part de l'hypothèse que les grappes sont sphériques, ce qui lui permet d'obtenir de bons résultats dans ce cas, alors que les groupes de taille et de densité différentes ne sont généralement pas bien pris en compte par cet algorithme. 

Lorsque ces conditions ne sont pas respectées, il est préférable de trouver d'autres approches alternatives, comme DBSCAN et BIRCH. Le regroupement dans l'apprentissage automatique : 5 algorithmes essentiels de clustering offre une excellente vue d'ensemble des approches de clustering, au cas où vous souhaiteriez approfondir la question.

Passez au niveau supérieur

Nous pouvons conclure que les k-moyennes restent l'un des algorithmes de regroupement les plus utilisés pour identifier des sous-groupes distincts, même s'il n'est pas toujours parfait dans toutes les situations. Maintenant, vous avez les connaissances nécessaires pour l'appliquer avec R dans d'autres études de cas. 

Si vous souhaitez approfondir cette méthode, jetez un coup d'œil au cours Unsupervised Learning in R. Il existe également Cluster Analysis in R et An Introduction to Hierarchical Clustering in Python pour avoir un aperçu complet des approches de clustering disponibles, ce qui peut être utile lorsque k-means n'est pas suffisant pour fournir des informations significatives à partir de vos données. Si vous souhaitez également explorer les modèles supervisés avec R, ce cours est recommandé !