Classification par K-Nearest Neighbors (KNN) avec scikit-learn

Bien que kNN puisse être utilisé pour la classification et la régression, cet article se concentrera sur la construction d'un modèle de classification. La classification dans l'apprentissage automatique est une tâche d'apprentissage supervisée qui consiste à prédire une étiquette catégorique pour un point de données d'entrée donné. L'algorithme est formé sur un ensemble de données étiquetées et utilise les caractéristiques d'entrée pour apprendre la correspondance entre les entrées et les étiquettes de classe correspondantes. Nous pouvons utiliser le modèle formé pour prédire de nouvelles données inédites. Vous pouvez également exécuter le code de ce tutoriel en ouvrant ce classeur DataLab. 

Aperçu des K-voisins les plus proches

L'algorithme kNN peut être considéré comme un système de vote, dans lequel l'étiquette de classe majoritaire détermine l'étiquette de classe d'un nouveau point de données parmi ses "k" (où k est un nombre entier) voisins les plus proches dans l'espace des caractéristiques. Imaginez un petit village de quelques centaines d'habitants, et vous devez décider pour quel parti politique vous devez voter. Pour ce faire, vous pouvez vous adresser à vos voisins les plus proches et leur demander quel parti politique ils soutiennent. Si la majorité de vos "k" voisins les plus proches soutiennent le parti A, il est fort probable que vous votiez également pour le parti A. Ce fonctionnement est similaire à celui de l'algorithme kNN, dans lequel l'étiquette de classe majoritaire détermine l'étiquette de classe d'un nouveau point de données parmi ses k voisins les plus proches.

Approfondissons la question avec un autre exemple. Imaginez que vous disposiez de données sur les fruits, en particulier les raisins et les poires. Vous obtenez un score pour la rondeur et le diamètre du fruit. Vous décidez de les représenter sur un graphique. Si quelqu'un vous tend un nouveau fruit, vous pouvez également l'inscrire sur le graphique, puis mesurer la distance entre k (un certain nombre) de points les plus proches pour déterminer de quel fruit il s'agit. Dans l'exemple ci-dessous, si nous choisissons de mesurer trois points, nous pouvons dire que les trois points les plus proches sont des poires, donc je suis sûr à 100 % qu'il s'agit d'une poire. Si nous choisissons de mesurer les quatre points les plus proches, trois d'entre eux sont des poires et le dernier est un raisin. Nous pouvons donc dire que nous sommes sûrs à 75 % qu'il s'agit d'une poire. Nous verrons plus loin dans cet article comment trouver la meilleure valeur pour k et les différentes façons de mesurer la distance.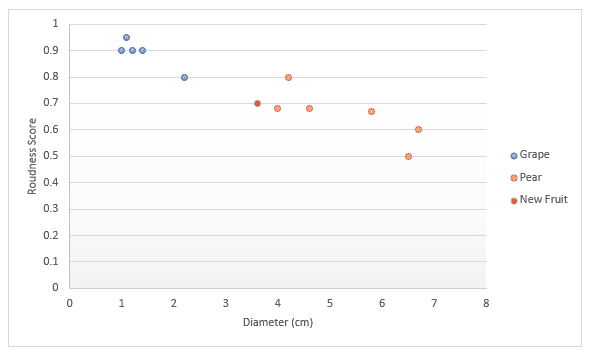

L'ensemble de données

Pour mieux illustrer l'algorithme kNN, nous allons travailler sur une étude de cas que vous pouvez rencontrer dans le cadre de votre travail en tant que scientifique des données. Supposons que vous soyez data scientist chez un détaillant en ligne et que vous soyez chargé de détecter les transactions frauduleuses. Les seules caractéristiques dont vous disposez à ce stade sont les suivantes :

• dist_from_home: La distance entre le domicile de l'utilisateur et le lieu où la transaction a été effectuée.
• purchase_price_ratio: le rapport entre le prix de l'article acheté lors de cette transaction et le prix d'achat médian de cet utilisateur.

Les données comportent 39 observations qui sont des transactions individuelles. Dans ce tutoriel, nous avons reçu l'ensemble de données, la variable df, qui ressemble à ceci :

Flux de travail des k-voisins les plus proches

Pour adapter et entraîner ce modèle, nous suivrons l'infographie The Machine Learning Workflow. 

Téléchargez l'infographie sur le flux de travail de l'apprentissage automatique 

Cependant, comme nos données sont assez propres, nous n'effectuerons pas toutes les étapes. Nous ferons ce qui suit :

• Ingénierie des fonctionnalités
• Diviser les données
• Former le modèle
• Réglage des hyperparamètres
• Évaluer la performance du modèle

Visualiser les données

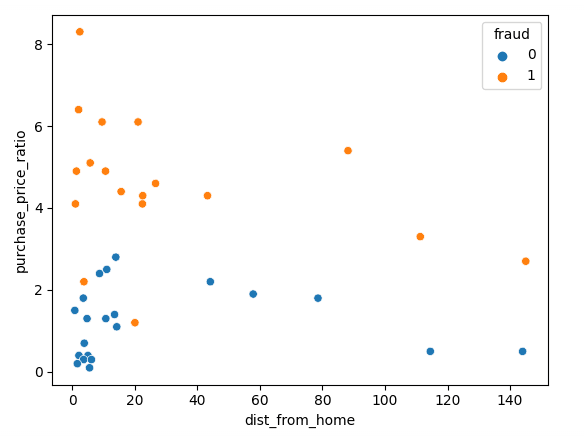
Commençons par visualiser nos données à l'aide de Matplotlib ; nous pouvons tracer nos deux caractéristiques dans un nuage de points.

sns.scatterplot(x=df['dist_from_home'],y=df['purchase_price_ratio'], hue=df['fraud'])

Comme vous pouvez le constater, il y a une nette différence entre ces transactions, les transactions frauduleuses étant d'une valeur beaucoup plus élevée que la commande médiane des clients. Les tendances relatives à la distance par rapport au domicile sont quelque peu difficiles à interpréter, les transactions non frauduleuses étant généralement plus proches du domicile, mais avec plusieurs valeurs aberrantes. 

Normaliser et diviser les données

Lors de l'apprentissage d'un modèle d'apprentissage automatique, il est important de diviser les données en données d'apprentissage et en données de test. Les données d'apprentissage sont utilisées pour ajuster le modèle. L'algorithme utilise les données d'apprentissage pour apprendre la relation entre les caractéristiques et la cible. Il tente de trouver un modèle dans les données d'apprentissage qui peut être utilisé pour faire des prédictions sur de nouvelles données inédites. Les données de test sont utilisées pour évaluer la performance du modèle. Le modèle est testé sur les données d'essai en l'utilisant pour faire des prédictions et en comparant ces prédictions aux valeurs cibles réelles. 

Lors de l'apprentissage d'un classificateur kNN, il est essentiel de normaliser les caractéristiques. En effet, kNN mesure la distance entre les points. La valeur par défaut est la distance euclidienne, qui correspond à la racine carrée de la somme des carrés des différences entre deux points. Dans notre cas, le rapport prix d'achat est compris entre 0 et 8 alors que la distance par rapport au domicile est beaucoup plus importante. Si nous ne normalisions pas ce chiffre, notre calcul serait fortement pondéré par dist_from_home parce que les chiffres sont plus importants.

Nous devons normaliser les données après les avoir divisées en ensembles de formation et de test. Cela permet d'éviter les "fuites de données", car la normalisation donnerait au modèle des informations supplémentaires sur l'ensemble de test si nous normalisions toutes les données en une seule fois.

Le code suivant divise les données en deux parties (train/test), puis les normalise en utilisant le scaler standard de scikit-learn. Nous appelons d'abord .fit_transform() sur les données d'apprentissage, qui ajuste notre échelle à la moyenne et à l'écart-type des données d'apprentissage. Nous pouvons ensuite l'appliquer aux données de test en appelant .transform(), qui utilise les valeurs apprises précédemment.

# Split the data into features (X) and target (y)
X = df.drop('fraud', axis=1)
y = df['fraud']

# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# Scale the features using StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

Ajustement et évaluation du modèle

Nous sommes maintenant prêts à former le modèle. Pour cela, nous utiliserons une valeur fixe de 3 pour k, mais nous devrons l'optimiser plus tard. Nous créons d'abord une instance du modèle kNN, puis nous l'adaptons à nos données d'apprentissage. Nous transmettons à la fois les caractéristiques et la variable cible, afin que le modèle puisse apprendre.

knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

Le modèle est maintenant formé ! Nous pouvons faire des prédictions sur l'ensemble de données de test, que nous pouvons utiliser ultérieurement pour évaluer le modèle.

y_pred = knn.predict(X_test)

La façon la plus simple d'évaluer ce modèle est d'utiliser la précision. Nous vérifions les prédictions par rapport aux valeurs réelles de l'ensemble de tests et comptons le nombre de valeurs correctes du modèle.

accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

Accuracy: 0.875

C'est un très bon score ! Cependant, nous pourrions faire mieux en optimisant notre valeur de k.

Utiliser la validation croisée pour obtenir la meilleure valeur de k

Malheureusement, il n'existe pas de méthode magique pour trouver la meilleure valeur pour k. Nous devons passer en revue un grand nombre de valeurs différentes, puis faire preuve de discernement.

Dans le code ci-dessous, nous sélectionnons une plage de valeurs pour k et créons une liste vide pour stocker nos résultats. Nous utilisons la validation croisée pour déterminer les scores de précision, ce qui signifie que nous n'avons pas besoin de créer une division de formation et de test, mais que nous devons mettre nos données à l'échelle. Nous passons ensuite en boucle sur les valeurs et ajoutons les scores à notre liste.

Pour mettre en œuvre la validation croisée, nous utilisons la fonction cross_val_score de scikit-learn. Nous transmettons une instance du modèle kNN, ainsi que nos données et un certain nombre de divisions à effectuer. Dans le code ci-dessous, nous utilisons cinq divisions, ce qui signifie que le modèle divise les données en cinq groupes de taille égale et en utilise quatre pour la formation et un pour le test. Il passera en boucle sur chaque groupe et donnera un score de précision, dont nous ferons la moyenne pour trouver le meilleur modèle.

k_values = [i for i in range (1,31)]
scores = []

scaler = StandardScaler()
X = scaler.fit_transform(X)

for k in k_values:
    knn = KNeighborsClassifier(n_neighbors=k)
    score = cross_val_score(knn, X, y, cv=5)
    scores.append(np.mean(score))

Nous pouvons tracer les résultats avec le code suivant

sns.lineplot(x = k_values, y = scores, marker = 'o')
plt.xlabel("K Values")
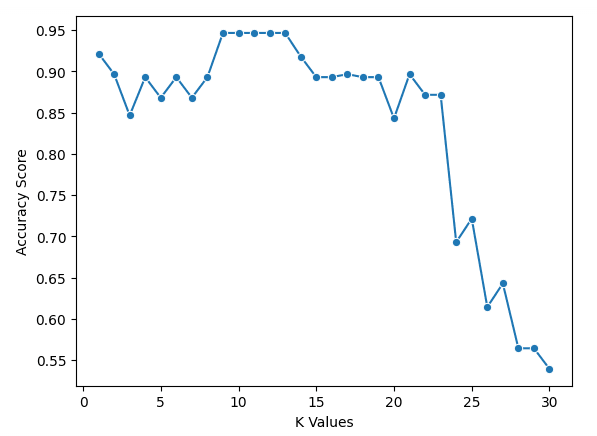
plt.ylabel("Accuracy Score")

Nous pouvons voir sur notre graphique que k = 9, 10, 11, 12 et 13 ont tous un score d'exactitude légèrement inférieur à 95 %. Comme ils sont ex aequo pour le meilleur score, il est conseillé d'utiliser une valeur plus petite pour k. En effet, lorsque les valeurs de k sont plus élevées, le modèle utilise davantage de points de données qui sont plus éloignés de l'original. Une autre option consisterait à explorer d'autres mesures d'évaluation.

Plus de mesures d'évaluation

Nous pouvons maintenant entraîner notre modèle en utilisant la meilleure valeur de k à l'aide du code ci-dessous.

best_index = np.argmax(scores)
best_k = k_values[best_index]

knn = KNeighborsClassifier(n_neighbors=best_k)
knn.fit(X_train, y_train)

évaluez ensuite l'exactitude, la précision et la mémorisation (notez que vos résultats peuvent différer en raison de la randomisation).

y_pred = knn.predict(X_test)

accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)

print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)

Accuracy: 0.875
Precision: 0.75
Recall: 1.0

Passez au niveau supérieur

• Le cours Supervised Learning with scikit-learn est le point d'entrée du programme d'apprentissage automatique en Python de DataCamp et couvre les voisins les plus proches (k-nearest neighbors).
• Les cours Détection d'anomalies en Python, Traitement des données manquantes en Python et Apprentissage automatique pour la finance en Python présentent tous des exemples d'utilisation des voisins les plus proches.
• Le tutoriel sur la classification par arbre de décision en Python traite d'un autre modèle d'apprentissage automatique pour la classification des données.
• L'aide-mémoire scikit-learn fournit une référence pratique pour les fonctionnalités les plus courantes de l'apprentissage automatique.