K-Nächste Nachbarn (KNN) Klassifizierung mit scikit-learn

Obwohl kNN für Klassifizierung und Regression verwendet werden kann, konzentriert sich dieser Artikel auf die Erstellung eines Klassifizierungsmodells. Die Klassifizierung beim maschinellen Lernen ist eine überwachte Lernaufgabe, bei der es darum geht, eine kategoriale Bezeichnung für einen bestimmten Eingabedatenpunkt vorherzusagen. Der Algorithmus wird auf einem gelabelten Datensatz trainiert und nutzt die Eingangsmerkmale, um die Zuordnung zwischen den Eingaben und den entsprechenden Klassenlabels zu lernen. Wir können das trainierte Modell verwenden, um neue, ungesehene Daten vorherzusagen. Du kannst den Code für diesen Lehrgang auch ausführen, indem du diese DataLab-Arbeitsmappe öffnest . 

Ein Überblick über K-Nächste Nachbarn

Der kNN-Algorithmus kann als ein Abstimmungssystem betrachtet werden, bei dem die Klassenbezeichnung der Mehrheit die Klassenbezeichnung eines neuen Datenpunktes unter seinen nächsten "k" (k ist eine ganze Zahl) Nachbarn im Merkmalsraum bestimmt. Stell dir ein kleines Dorf mit ein paar hundert Einwohnern vor, und du musst dich entscheiden, welche politische Partei du wählen sollst. Dazu könntest du zu deinen nächsten Nachbarn gehen und sie fragen, welche politische Partei sie unterstützen. Wenn die Mehrheit deiner k nächsten Nachbarn die Partei A unterstützt, würdest du höchstwahrscheinlich auch für die Partei A stimmen. Das ist ähnlich wie beim kNN-Algorithmus, bei dem die Klassenbezeichnung der Mehrheit unter den k nächsten Nachbarn die Klassenbezeichnung eines neuen Datenpunkts bestimmt.

Schauen wir uns das Ganze an einem anderen Beispiel genauer an. Stell dir vor, du hast Daten über Obst, insbesondere Trauben und Birnen. Du bekommst eine Punktzahl dafür, wie rund die Frucht ist und welchen Durchmesser sie hat. Du beschließt, diese in ein Diagramm einzutragen. Wenn dir jemand eine neue Frucht in die Hand drückt, könntest du diese ebenfalls in das Diagramm eintragen und dann den Abstand zu k (einer Anzahl) nächstgelegenen Punkten messen, um zu entscheiden, welche Frucht es ist. Wenn wir im folgenden Beispiel drei Punkte messen, können wir sagen, dass die drei nächstgelegenen Punkte Birnen sind, also bin ich mir zu 100% sicher, dass es sich um eine Birne handelt. Wenn wir uns entscheiden, die vier nächstgelegenen Punkte zu messen, sind drei davon Birnen und einer eine Weintraube. Wir sind also zu 75% sicher, dass es sich um eine Birne handelt. Wie du den besten Wert für k findest und welche verschiedenen Möglichkeiten es gibt, den Abstand zu messen, werden wir später in diesem Artikel behandeln.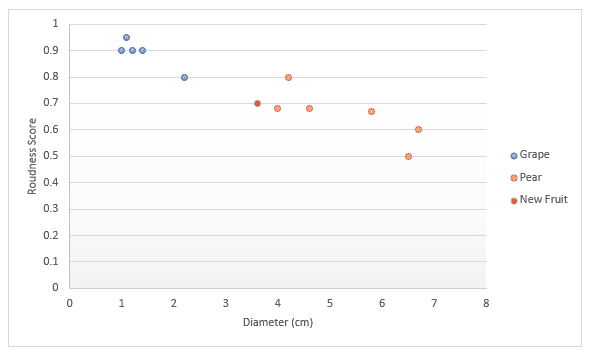

Der Datensatz

Zur weiteren Veranschaulichung des kNN-Algorithmus arbeiten wir mit einer Fallstudie, die du bei deiner Arbeit als Datenwissenschaftler/in finden kannst. Nehmen wir an, du bist Datenwissenschaftler/in bei einem Online-Händler und hast die Aufgabe, betrügerische Transaktionen zu erkennen. Die einzigen Merkmale, die du in diesem Stadium hast, sind:

• dist_from_home: Die Entfernung zwischen dem Wohnort des Nutzers und dem Ort, an dem die Transaktion getätigt wurde.
• purchase_price_ratio: das Verhältnis zwischen dem Preis des Artikels, der in dieser Transaktion gekauft wurde, und dem Median des Kaufpreises dieses Nutzers.

Die Daten enthalten 39 Beobachtungen, die einzelne Transaktionen darstellen. In diesem Lernprogramm haben wir den Datensatz mit der Variable df erhalten, die wie folgt aussieht:

k-Nächste-Nachbarn-Arbeitsablauf

Um dieses Modell anzupassen und zu trainieren, folgen wir der Infografik The Machine Learning Workflow. 

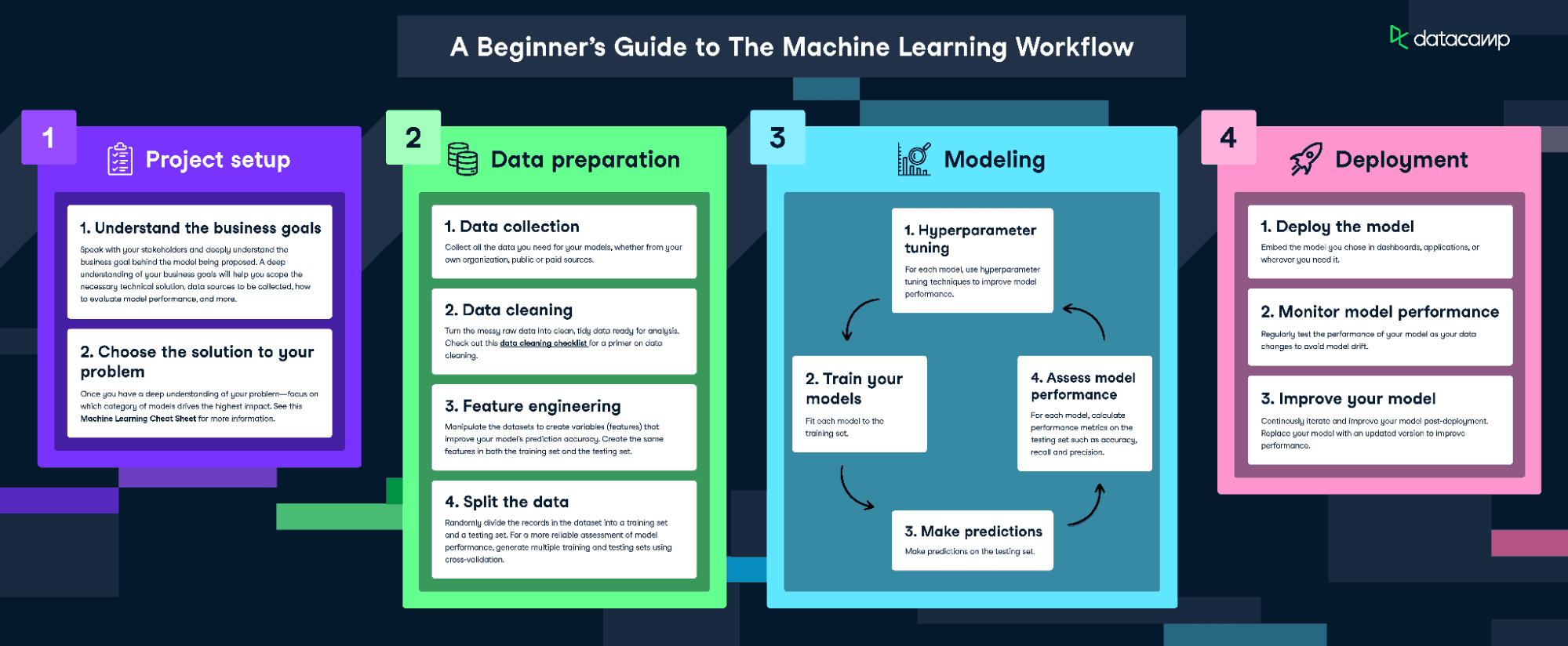
Lade die Infografik zum maschinellen Lernen herunter 

Da unsere Daten aber ziemlich sauber sind, werden wir nicht jeden Schritt ausführen. Wir werden Folgendes tun:

• Feature Engineering
• Aufteilung der Daten
• Das Modell trainieren
• Hyperparameter-Abstimmung
• Modellleistung bewerten

Visualisiere die Daten

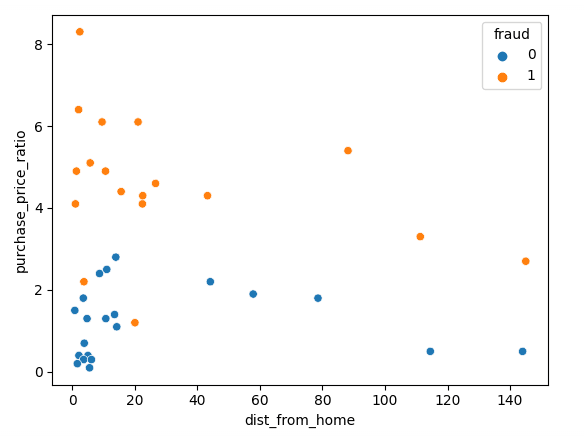
Beginnen wir damit, unsere Daten mit Matplotlib zu visualisieren; wir können unsere beiden Merkmale in einem Scatterplot darstellen.

sns.scatterplot(x=df['dist_from_home'],y=df['purchase_price_ratio'], hue=df['fraud'])

Wie du siehst, gibt es einen deutlichen Unterschied zwischen diesen Transaktionen, wobei die betrügerischen Transaktionen im Vergleich zur durchschnittlichen Bestellung der Kunden einen viel höheren Wert haben. Die Trends in Bezug auf die Entfernung zum Wohnort sind etwas schwer zu interpretieren: Nicht betrügerische Transaktionen liegen in der Regel näher am Wohnort, aber es gibt auch einige Ausreißer. 

Normalisieren und Aufteilen der Daten

Wenn du ein maschinelles Lernmodell trainierst, ist es wichtig, die Daten in Trainings- und Testdaten aufzuteilen. Die Trainingsdaten werden verwendet, um das Modell anzupassen. Der Algorithmus nutzt die Trainingsdaten, um die Beziehung zwischen den Merkmalen und dem Ziel zu lernen. Sie versucht, in den Trainingsdaten ein Muster zu finden, das für Vorhersagen über neue, ungesehene Daten verwendet werden kann. Die Testdaten werden verwendet, um die Leistung des Modells zu bewerten. Das Modell wird an den Testdaten getestet, indem es für Vorhersagen verwendet wird und diese Vorhersagen mit den tatsächlichen Zielwerten verglichen werden. 

Wenn du einen kNN-Klassifikator trainierst, ist es wichtig, die Merkmale zu normalisieren. Das liegt daran, dass kNN den Abstand zwischen Punkten misst. Standardmäßig wird der euklidische Abstand verwendet, der die Quadratwurzel aus der Summe der quadrierten Differenzen zwischen zwei Punkten ist. In unserem Fall liegt die purchase_price_ratio zwischen 0 und 8, während die dist_from_home viel größer ist. Wenn wir das nicht normalisieren würden, würde unsere Berechnung stark nach der Entfernung vom Wohnort gewichtet werden, weil die Zahlen größer sind.

Wir sollten die Daten normalisieren, nachdem wir sie in Trainings- und Testgruppen aufgeteilt haben. Damit soll ein "Datenleck" verhindert werden, denn die Normalisierung würde dem Modell zusätzliche Informationen über die Testmenge liefern, wenn wir alle Daten auf einmal normalisieren würden.

Der folgende Code teilt die Daten in Trainings- und Test-Splits auf und normalisiert sie dann mit dem Standard-Skalierer von Scikit-Learn. Zuerst rufen wir .fit_transform() für die Trainingsdaten auf, die unseren Skalierer an den Mittelwert und die Standardabweichung der Trainingsdaten anpasst. Wir können dies dann auf die Testdaten anwenden, indem wir .transform() aufrufen, das die zuvor gelernten Werte verwendet.

# Split the data into features (X) and target (y)
X = df.drop('fraud', axis=1)
y = df['fraud']

# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# Scale the features using StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

Anpassen und Auswerten des Modells

Wir sind jetzt bereit, das Modell zu trainieren. Wir verwenden einen festen Wert von 3 für k, aber wir werden diesen Wert später noch optimieren müssen. Wir erstellen zunächst eine Instanz des kNN-Modells und passen diese dann an unsere Trainingsdaten an. Wir übergeben sowohl die Merkmale als auch die Zielvariable, damit das Modell lernen kann.

knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

Das Modell ist jetzt trainiert! Wir können Vorhersagen für den Testdatensatz machen, die wir später zur Bewertung des Modells verwenden können.

y_pred = knn.predict(X_test)

Der einfachste Weg, dieses Modell zu bewerten, ist die Genauigkeit. Wir vergleichen die Vorhersagen mit den tatsächlichen Werten in der Testmenge und zählen, wie viele das Modell richtig lag.

accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

Accuracy: 0.875

Das ist ein ziemlich gutes Ergebnis! Vielleicht können wir aber noch mehr erreichen, wenn wir unseren Wert für k optimieren.

Mit der Kreuzvalidierung den besten Wert von k erhalten

Leider gibt es keinen Königsweg, um den besten Wert für k zu finden. Wir müssen viele verschiedene Werte durchgehen und dann unser bestes Urteilsvermögen einsetzen.

Im folgenden Code wählen wir einen Wertebereich für k aus und erstellen eine leere Liste, um unsere Ergebnisse zu speichern. Wir verwenden die Kreuzvalidierung, um die Genauigkeitswerte zu ermitteln. Das bedeutet, dass wir keine Aufteilung in Trainings- und Testdaten vornehmen müssen, aber wir müssen unsere Daten skalieren. Dann gehen wir die Werte in einer Schleife durch und fügen die Punkte zu unserer Liste hinzu.

Um die Kreuzvalidierung zu implementieren, verwenden wir den cross_val_score von scikit-learn. Wir übergeben eine Instanz des kNN-Modells zusammen mit unseren Daten und einer Anzahl von Splits, die wir machen müssen. Im folgenden Code verwenden wir fünf Splits, was bedeutet, dass das Modell die Daten in fünf gleich große Gruppen aufteilt und 4 zum Trainieren und 1 zum Testen der Ergebnisse verwendet. Es geht in einer Schleife durch jede Gruppe und gibt eine Trefferquote an, aus der wir den Durchschnitt bilden, um das beste Modell zu finden.

k_values = [i for i in range (1,31)]
scores = []

scaler = StandardScaler()
X = scaler.fit_transform(X)

for k in k_values:
    knn = KNeighborsClassifier(n_neighbors=k)
    score = cross_val_score(knn, X, y, cv=5)
    scores.append(np.mean(score))

Wir können die Ergebnisse mit folgendem Code darstellen

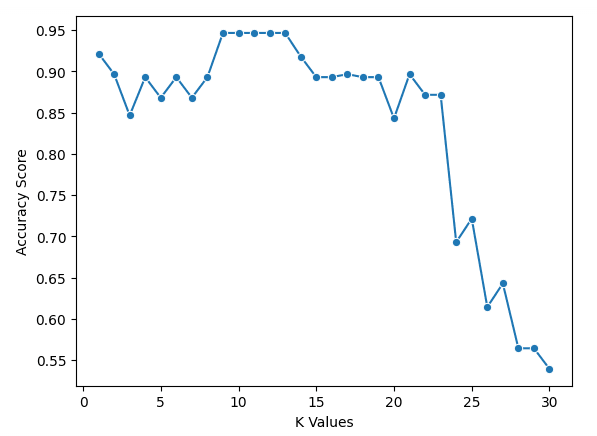
sns.lineplot(x = k_values, y = scores, marker = 'o')
plt.xlabel("K Values")
plt.ylabel("Accuracy Score")

Aus unserer Tabelle können wir ersehen, dass k = 9, 10, 11, 12 und 13 alle eine Genauigkeit von knapp 95% haben. Da diese für die beste Punktzahl gleichauf sind, ist es ratsam, einen kleineren Wert für k zu verwenden. Das liegt daran, dass das Modell bei höheren Werten von k mehr Datenpunkte verwendet, die weiter vom Original entfernt sind. Eine andere Möglichkeit wäre, andere Bewertungsmaßstäbe zu untersuchen.

Weitere Bewertungsmetriken

Jetzt können wir unser Modell mit dem besten k-Wert trainieren, indem wir den folgenden Code verwenden.

best_index = np.argmax(scores)
best_k = k_values[best_index]

knn = KNeighborsClassifier(n_neighbors=best_k)
knn.fit(X_train, y_train)

dann mit Genauigkeit, Präzision und Wiedererkennung auswerten (beachte, dass deine Ergebnisse aufgrund der Randomisierung abweichen können)

y_pred = knn.predict(X_test)

accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)

print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)

Accuracy: 0.875
Precision: 0.75
Recall: 1.0

Bring es auf die nächste Stufe

• Der Kurs Supervised Learning with scikit-learn ist der Einstieg in den DataCamp-Lehrplan für maschinelles Lernen in Python und behandelt k-nearest neighbors.
• Die Kurse "Anomaly Detection in Python", " Dealing with Missing Data in Python" und "Machine Learning for Finance in Python " zeigen Beispiele für die Verwendung von k-nearest neighbors.
• Das Tutorial Entscheidungsbaum-Klassifizierung in Python behandelt ein weiteres maschinelles Lernmodell zur Klassifizierung von Daten.
• Der scikit-learn Spickzettel bietet eine praktische Referenz für beliebte Funktionen des maschinellen Lernens.