Analyse discriminante linéaire : Au-delà de la réduction dimensionnelle

L'analyse discriminante linéaire (LDA) est souvent éclipsée par un algorithme plus populaire, l'analyse en composantes principales (ACP), lorsqu'il s'agit de réduction de dimensionnalité. Cependant, l'analyse en dimensions latentes offre un avantage unique que l'analyse en composantes principales ne peut pas fournir : elle réduit les dimensions tout en optimisant la séparabilité des classes.

Ce tutoriel vous présentera la LDA, l'intuition mathématique qui la sous-tend et les applications concrètes de cette technique. En outre, nous mettrons en œuvre la LDA sur un ensemble de données, la comparerons à la PCA et analyserons ses avantages et ses inconvénients, dans le but de vous fournir tout ce dont vous avez besoin pour commencer à appliquer la LDA dans votre prochain projet.

Introduction à l'analyse discriminante linéaire (LDA)

La LDA est une technique de réduction de dimension et de classification qui part du principe que différentes classes génèrent des données basées sur différentes distributions gaussiennes. 

L'analyse des composantes principales (LDA) vise à trouver une combinaison linéaire de caractéristiques qui sépare le mieux ces classes. Il maximise le rapport entre la dispersion interclasses et la dispersion intraclasse. En termes plus simples, il s'agit de trouver des directions dans l'espace des caractéristiques où les différentes classes sont éloignées les unes des autres (dispersion inter-classes élevée) tandis que les points appartenant à une même classe sont proches les uns des autres (dispersion intra-classes faible). 

Ce double objectif rend l'analyse LDA particulièrement efficace pour les tâches de réduction de dimensionnalité et de classification.

Les mathématiques derrière l'analyse LDA

Pour comprendre les mathématiques qui sous-tendent l'algorithme LDA, il est nécessaire de le décomposer en trois éléments clés : 

• dispersion intraclasse, 
• dispersion interclasses, et
• objectif d'optimisation.

Matrice de dispersion intraclasse (Sw)

La matrice de dispersion intraclasse mesure le degré de dispersion des points de données au sein de chaque classe. 

Pour chaque classe i, nous calculons la matrice de dispersion Si comme suit :

Si = Σ(x - μi)(x - μi)T

Où x représente chaque point de données dans la classe i, et μi est la moyenne de la classe i. La matrice de dispersion totale au sein de la classe est la suivante :

Sw = Σ Si (sum over all classes)

Matrice de dispersion interclasses (Sb)

La matrice de dispersion interclasses mesure l'écart entre les moyennes des classes et la moyenne globale. Il est calculé comme suit :

Sb = Σ Ni(μi - μ)(μi - μ)T  

Où Ni est le nombre d'échantillons dans la classe i, μi est la moyenne de la classe i et μ est la moyenne globale de toutes les données.

Objectif d'optimisation

LDA cherche à trouver la matrice de projection W qui maximise le critère de Fisher :

J(W) = |WT Sb W| / |WT Sw W|

Il s'agit essentiellement de maximiser le rapport entre la dispersion interclasses et la dispersion intraclasse dans l'espace projeté. La solution consiste à trouver les vecteurs propres de la matrice ^Sw-1Sb, qui nous donnent les directions (discriminantes linéaires) qui séparent le mieux les classes.

Ainsi, la LDA réduit ce problème d'optimisation complexe à une décomposition en valeurs propres, ce qui la rendefficace sur le plan informatique, même pour des ensembles de données de dimension modérément élevée.

Maintenant que nous avons compris le concept et l'intuition mathématique derrière la LDA, découvrons ses applications concrètes.

Applications concrètes de la LDA

La LDA trouve des applications dans plusieurs domaines où la classification et la réduction de la dimensionnalité sont nécessaires :

• s relatives au diagnostic médical: La LDA est utilisée en imagerie médicale pour classer différents types de tumeurs ou d'anomalies. Il est capable d'analyser des images IRM afin de distinguer les tissus bénins des tissus malins en identifiant les caractéristiques les plus discriminantes dans les données d'image.
• s financières et bancaires: Les systèmes de notation de crédit utilisent l'analyse LDA pour classer les demandeurs de prêt dans différentes catégories de risque. En analysant des indicateurs financiers tels que les revenus, le ratio dette/revenu et les antécédents de crédit, LDA peut aider à distinguer les emprunteurs à haut risque de ceux à faible risque.
• s bioinformatiques: L'analyse de l'expression génique utilise la LDA pour classer différents états pathologiques ou différentes réponses à un traitement. Il aide à identifier les gènes les plus importants pour distinguer les échantillons de tissus sains des échantillons de tissus malades.
• s en matière de marketing et de segmentation de la clientèle: Les entreprises utilisent l'analyse LDA pour segmenter leurs clients en fonction de leur comportement d'achat, de leurs données démographiques et de leurs indicateurs d'engagement. Cela s'avère utile dans le cadre de campagnes marketing ciblées et de recommandations de produits personnalisées.
• s de reconnaissance d'images: Les systèmes de reconnaissance faciale utilisent l'analyse en dimensions faibles (LDA) pour réduire la dimensionnalité des images faciales tout en conservant les caractéristiques les plus importantes pour distinguer les individus.
• du contrôle qualité: Les industries manufacturières utilisent l'analyse de distribution de fréquences (LDA) pour classer les produits comme défectueux ou non défectueux en fonction de divers indicateurs de qualité, ce qui permet d'automatiser les processus d'assurance qualité.
• s de reconnaissance vocale: L'analyse des mots (LDA) facilite la classification des phonèmes en identifiant les caractéristiques acoustiques qui permettent de distinguer le mieux les différents sons de la parole, améliorant ainsi la précision des systèmes de reconnaissance vocale.
• s de surveillance environnementale: L'analyse des classes latentes (LDA) est utilisée pour classer les conditions environnementales à partir de données fournies par des capteurs, par exemple pour distinguer différents niveaux de pollution ou différents types de conditions météorologiques.

Implémentation de LDA en Python

Examinons un exemple complet de mise en œuvre de LDA à l'aide de Python. 

Nous utiliserons l'ensemble de données Seeds, qui peut être téléchargé depuis la bibliothèque UCI ainsi que depuis Kaggle. L'ensemble de donnéescontient des mesures de grains de blé appartenant à trois variétés différentes de blé.

Étape 1 : Importez les bibliothèques et chargez les données.

Tout d'abord, nous allons importer les bibliothèques nécessaires et charger notre ensemble de données :

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score

# Load the seeds dataset
file_path = "seeds_dataset.txt"
column_names = ['area', 'perimeter', 'compactness', 'kernel_length',
               'kernel_width', 'asymmetry', 'groove_length', 'variety']

# Read the data with whitespace delimiter (space or tab)
seeds_df = pd.read_csv(file_path, sep='\s+', header=None, names=column_names)

print(f"Dataset shape: {seeds_df.shape}")
seeds_df.head()

Nous allons voir les 5 premières lignes de l'ensemble de données chargé ci-dessous :

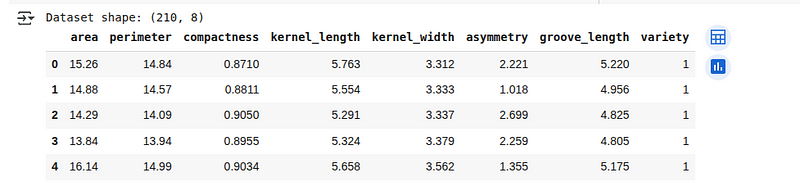Aperçu de l'ensemble de données Seeds. (Image par l'auteur)

Étape 2 : Pré-traitement des données

Explorons la structure des données et préparons-la pour l'analyse LDA :

# Check for missing values
print(f"Missing values: {seeds_df.isnull().sum().sum()}")

# Check class distribution
print("\nClass distribution:")
print(seeds_df['variety'].value_counts())

# Separate features and target
X = seeds_df.drop('variety', axis=1)
y = seeds_df['variety']

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
                                                   random_state=42, stratify=y)

# Standardize the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

Ici, nous vérifions si l'ensemble de données comporte des valeurs manquantes et examinons combien d'exemples appartiennent à chaque catégorie. Ensuite, nous préparons les données en séparant les entrées des étiquettes, en les divisant en deux parties (entraînement et test) et en normalisant les valeurs d'entrée afin que toutes les caractéristiques soient sur une échelle similaire.

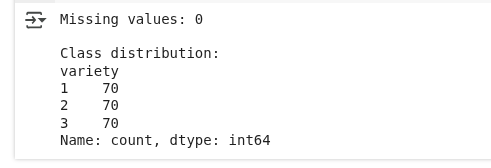
Pré-traitement des données. (Image par l'auteur)

Nous constatons qu'il n'y a pas de valeurs manquantes et que la répartition des classes est égale.

Étape 3 : Application de la LDA pour la réduction de la dimensionnalité

Nous allons maintenant appliquer la LDA pour réduire la dimensionnalité de nos données tout en préservant la séparabilité des classes :

# Create and fit LDA model
lda = LinearDiscriminantAnalysis(n_components=2)
X_train_lda = lda.fit_transform(X_train_scaled, y_train)
X_test_lda = lda.transform(X_test_scaled)

# Print explained variance ratio
print("Explained variance ratio:", lda.explained_variance_ratio_)
print("Cumulative explained variance:", np.cumsum(lda.explained_variance_ratio_))

Nous élaborons un modèle qui identifie les meilleures orientations pour séparer les différentes catégories dans nos données. En réduisant les données à deux nouvelles caractéristiques (puisque nous avons trois catégories), nous conservons les modèles les plus importants pour les distinguer.

Le résultat est le suivant :

Résultats de la variance LDA. (Image par l'auteur)

Cette sortie montre la proportion d'informations permettant de distinguer les classes qui est capturée par les deux nouvelles caractéristiques créées par LDA :

• Ratio de variance expliquée : Cela signifie que la première composante LDA capture environ 67,7 % des informations nécessaires pour distinguer les classes, tandis que la deuxième composante capture les 32,3 % restants.
• Variance cumulée expliquée : Ensemble, ces deux composantes capturent 100 % des informations permettant de distinguer les classes dans les données d'origine. Ceci est prévisible, car nous avons trois classes et l'algorithme LDA fournit au maximum deux directions utiles.

Étape 4 : Visualiser la transformation LDA

Visualisons comment l'algorithme LDA transforme nos données et sépare les classes :

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# Plot the first two original features
ax1.scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
           c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax1.set_xlabel('Area (standardized)')
ax1.set_ylabel('Perimeter (standardized)')
ax1.set_title('Original Feature Space (First Two Features)')
ax1.grid(True, alpha=0.3)

# Plot LDA-transformed data
scatter = ax2.scatter(X_train_lda[:, 0], X_train_lda[:, 1],
                     c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax2.set_xlabel('First Linear Discriminant')
ax2.set_ylabel('Second Linear Discriminant')
ax2.set_title('LDA-Transformed Space')
ax2.grid(True, alpha=0.3)

plt.colorbar(scatter, ax=ax2, label='Wheat Variety')
plt.tight_layout()
plt.show()

Le code ci-dessus crée deux graphiques côte à côte afin de nous aider à comparer l'aspect des données avant et après l'application de la technique de réduction de dimensionnalité, comme illustré ci-dessous :

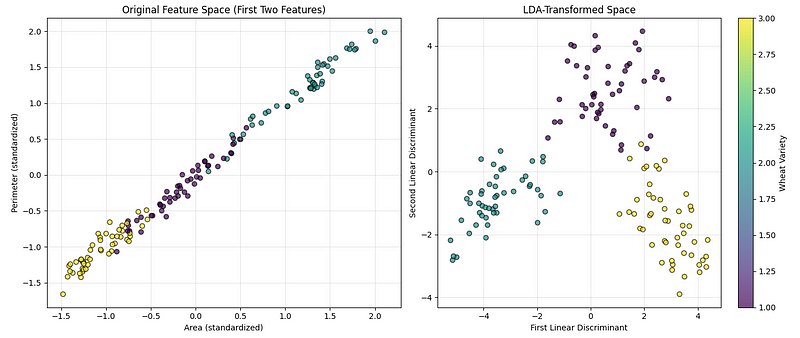Visualisation LDA d'. (Image par l'auteur)

Le premier graphique présente les données originales à l'aide de deux des caractéristiques mesurées (surface et périmètre), ce qui nous permet de voir dans quelle mesure les catégories sont naturellement séparées. Le deuxième graphique présente les données après les avoir transformées dans les directions les plus informatives pour séparer les catégories. Une barre de couleurs est ajoutée pour indiquer quelle couleur correspond à quel type de blé.

Étape 5 : Utiliser LDA pour la classification

L'analyse LDA peut également être utilisée directement comme classificateur. 

Mettons cela en pratique :

# Create LDA classifier
lda_classifier = LinearDiscriminantAnalysis()
lda_classifier.fit(X_train_scaled, y_train)

# Make predictions
y_pred = lda_classifier.predict(X_test_scaled)

# Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f"Classification Accuracy: {accuracy:.4f}")

# Print classification report
print("\nClassification Report:")
print(classification_report(y_test, y_pred))

Nous formons un modèle afin qu'il reconnaisse les différentes catégories de blé à partir des données d'entraînement. Nous évaluons ensuite ses performances sur de nouveaux exemples inédits en vérifiant sa précision globale et sa capacité à prédire chaque catégorie.

Nous observons le résultat suivant :

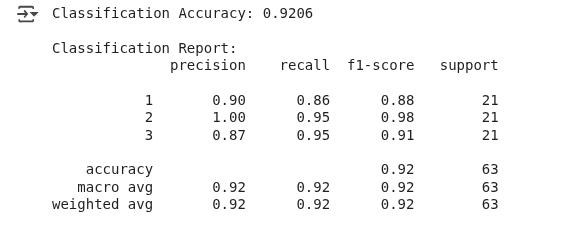
Résultats de la classification LDA. (Image par l'auteur)

Le modèle a correctement prédit le type de blé dans environ 92 % des cas, ce qui peut être considéré comme une bonne performance. 

Cet exemple a démontré que, bien que la LDA soit couramment utilisée pour la réduction de dimensionnalité, elle peut également servir de classificateur en modélisant la distribution de probabilité de chaque classe et en attribuant les nouvelles données à la classe présentant la probabilité la plus élevée.

Comparaison entre LDA et ACP avec codes et visualisations

L'analyse en composantes principales est une autre technique populaire de réduction de la dimensionnalité qui permet de déterminer les directions de variance maximale dans les données. 

Poursuivons notre exemple précédent pour comparer la LDA à la PCA :

à partir de sklearn.decomposition import PCA

# Apply PCA with 2 components
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
X_test_pca = pca.transform(X_test_scaled)

# Create comparison visualization
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# Plot PCA results
scatter1 = ax1.scatter(X_train_pca[:, 0], X_train_pca[:, 1],
                      c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax1.set_xlabel('First Principal Component')
ax1.set_ylabel('Second Principal Component')
ax1.set_title(f'PCA Transformation\nExplained Variance: {pca.explained_variance_ratio_.sum():.2%}')
ax1.grid(True, alpha=0.3)

# Plot LDA results
scatter2 = ax2.scatter(X_train_lda[:, 0], X_train_lda[:, 1],
                      c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax2.set_xlabel('First Linear Discriminant')
ax2.set_ylabel('Second Linear Discriminant')
ax2.set_title(f'LDA Transformation\nExplained Variance: {lda.explained_variance_ratio_.sum():.2%}')
ax2.grid(True, alpha=0.3)

plt.colorbar(scatter1, ax=ax1, label='Wheat Variety')
plt.colorbar(scatter2, ax=ax2, label='Wheat Variety')
plt.tight_layout()
plt.show()

Nous observons le graphique suivant :

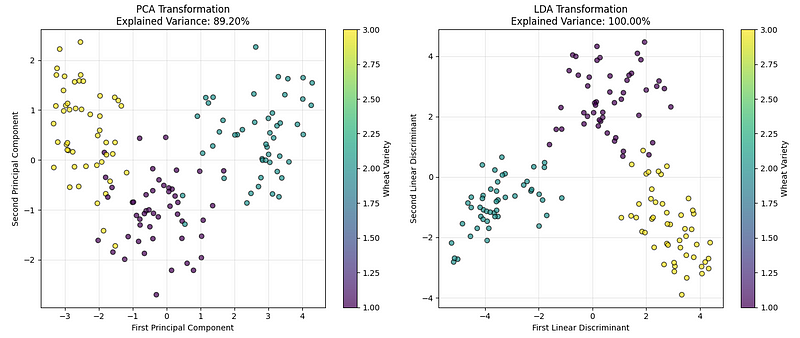LDA vs. Comparaison PCA. (Image par l'auteur)

Le graphique de gauche présente les données à l'aide de l'ACP, qui identifie les directions qui capturent la plus grande variation globale dans les données. Le graphique de droite présente le résultat de l'analyse LDA, qui identifie les directions qui permettent de mieux distinguer les catégories de blé.

Sur la base de nos résultats de mise en œuvre et des valeurs de variance expliquées, nous pouvons conclure que, bien que les deux méthodes fonctionnent bien, pour des problèmes de classification comme celui-ci, la LDA permet généralement d'établir une séparation plus claire entre les groupes.

Ce qui distingue la LDA des autres techniques de réduction de dimensionnalité, c'est sa nature supervisée. Alors que l'ACP ne tient compte que de la variance des données sans tenir compte des étiquettes de classe, la LDA utilise explicitement les informations de classe pour trouver les directions les plus discriminantes. Ceci est particulièrement utile lorsque l'on traite des données à haute dimension, où la séparabilité des classes est plus importante que la préservation de la variance globale.

Ainsi, l'ACP peut être utilisée lorsque :

• Nous avons besoin d'une réduction de la dimensionnalité non supervisée.
• Les étiquettes de classe ne sont pas disponibles ou ne sont pas pertinentes.
• Nous souhaitons visualiser des données à haute dimension.
• Il est nécessaire de réduire le bruit et la complexité des calculs.

De même, nous pouvons utiliser la LDA lorsque :

• Nous disposons de données étiquetées et souhaitons optimiser la séparation des classes.
• Le nombre d'échantillons par classe est suffisant (généralement supérieur à 30).
• Nous avons besoin à la fois d'une réduction de la dimensionnalité et d'une classification.
• La discrimination de classe est plus importante que la préservation de la variance globale.

Avantages et inconvénients de la LDA

Comme tout algorithme, le LDA présente des avantages et des limites dont il convient de tenir compte avant de l'appliquer à nos projets.

Avantages

• Avantages de l'apprentissage supervisé: Contrairement à l'ACP, l'AAL utilise les informations relatives aux étiquettes de classe pour trouver les caractéristiques les plus discriminantes, ce qui la rend plus efficace pour les tâches de classification.
• Réduction de la dimensionnalité avec classification: Il remplit une double fonction : réduire les dimensions tout en fournissant un classificateur intégré.
• Efficacité informatique: Nécessite uniquement une décomposition en valeurs propres, ce qui le rend rapide même pour des ensembles de données de taille moyenne.
• s en matière d'interprétabilité: Les discriminants linéaires peuvent être interprétés comme des combinaisons pondérées des caractéristiques originales.
• Optimal pour les distributions gaussiennes: Il fournit le classificateur linéaire optimal lorsque les classes suivent des distributions gaussiennes avec des matrices de covariance égales.
• Aucun réglage des hyperparamètres n': Contrairement à de nombreux algorithmes d'apprentissage automatique, LDA ne nécessite aucun hyperparamètre à régler pour une implémentation de base.

Inconvénients

• Limites linéaires uniquement: Impossible de capturer les relations non linéaires entre les caractéristiques et les classes.
• s de l'hypothèse de covariance gaussienne et égale: Supposons que chaque classe suit une distribution gaussienne multivariée, ce qui peut ne pas être le cas pour des données réelles, et supposons que toutes les classes ont la même matrice de covariance, ce qui est souvent contraire à la pratique.
• s des composants: Peut extraire au maximum (n_classes — 1) composantes discriminantes, ce qui peut s'avérer insuffisant pour la visualisation dans le cas de problèmes multi-classes.
• Sensible aux valeurs aberrantes et aux problèmes de multicolinéarité.: Les calculs de moyenne et de covariance sont sensibles aux valeurs aberrantes, et l'algorithme peut fonctionner de manière insatisfaisante lorsque les caractéristiques sont fortement corrélées.
• Exigences relatives à la taille de l'échantillon: Nécessite un nombre suffisant d'échantillons par classe pour estimer de manière fiable les matrices de covariance.

La compréhension de ces compromis nous aide à déterminer si l'algorithme LDA est le plus adapté au problème à résoudre.

Conclusion

Cet article a présenté l'analyse discriminante linéaire, une technique supervisée qui combine la réduction de dimensionnalité et la classification en maximisant le rapport entre la dispersion interclasses et la dispersion intraclasse.

Nous avons exploré les fondements mathématiques de la LDA, l'avons mise en œuvre à l'aide de Python et l'avons comparée à la PCA afin de comprendre quand chaque technique est la plus appropriée. Nous avons également découvert les applications concrètes de la LDA et discuté de ses avantages et de ses limites.

Pour approfondir vos connaissances sur le LDA et les techniques d'apprentissage automatique associées, nous vous recommandons de vous inscrire à notre cursus Apprentissage automatique supervisé avec Python, qui vous permettra de maîtriser divers algorithmes et leurs implémentations, ou à notre cours Réduction de la dimensionnalité avec Python, qui vous permettra d'approfondir vos connaissances sur les techniques de réduction de dimensionnalité supervisées et non supervisées.