Lineare Diskriminanzanalyse: Mehr als nur Dimensionsreduktion

Die lineare Diskriminanzanalyse (LDA) wird oft von einem bekannteren Algorithmus, der Hauptkomponentenanalyse (PCA), in den Schatten gestellt, wenn es um Dimensionsreduktion geht. Aber LDA hat was, was PCA nicht kann: Es reduziert die Dimensionen und optimiert gleichzeitig die Klassentrennbarkeit.

In diesem Tutorial lernst du LDA kennen, die mathematische Idee dahinter und wie man das Ganze in der Praxis anwendet. Außerdem werden wir LDA auf einen Datensatz anwenden, es mit PCA vergleichen und seine Vor- und Nachteile analysieren, damit du alles hast, was du brauchst, um LDA in deinem nächsten Projekt einzusetzen.

Einführung in die lineare Diskriminanzanalyse (LDA)

LDA ist eine Technik zur Dimensionsreduktion und Klassifizierung, die davon ausgeht, dass verschiedene Klassen Daten basierend auf unterschiedlichen Gaußschen Verteilungen erzeugen. 

LDA versucht, eine lineare Kombination von Merkmalen zu finden, die diese Klassen am besten voneinander trennt. Es maximiert das Verhältnis zwischen der Streuung innerhalb einer Klasse und der Streuung zwischen den Klassen. Einfacher gesagt: Es sucht nach Richtungen im Merkmalsraum, wo verschiedene Klassen weit voneinander entfernt sind (hohe Streuung zwischen den Klassen), während Punkte innerhalb derselben Klasse nah beieinander liegen (geringe Streuung innerhalb der Klasse). 

Dieses doppelte Ziel macht LDA besonders gut für Aufgaben zur Dimensionsreduktion und Klassifizierung.

Die Mathe hinter der LDA

Um die Mathe hinter LDA zu verstehen, muss man den Algorithmus in drei Hauptteile aufteilen: 

• Streuung innerhalb der Klasse, 
• Streuung zwischen den Klassen und
• Optimierungsziel.

Streumatrix innerhalb der Klasse (Sw)

Die Streuungsmatrix innerhalb einer Klasse zeigt, wie weit die Datenpunkte innerhalb jeder Klasse auseinander liegen. 

Für jede Klasse i berechnen wir die Streuungsmatrix Si wie folgt:

Si = Σ(x - μi)(x - μi)T

Wobei x jeden Datenpunkt in Klasse i darstellt und μi der Mittelwert von Klasse i ist. Die Gesamtstreuungsmatrix innerhalb der Klasse ist:

Sw = Σ Si (sum over all classes)

Streumatrix zwischen Klassen (Sb)

Die Streuungsmatrix zwischen den Klassen zeigt, wie weit die Klassenmittelwerte vom Gesamtmittelwert entfernt sind. Die Berechnung geht so:

Sb = Σ Ni(μi - μ)(μi - μ)T  

Dabei ist Ni die Anzahl der Proben in Klasse i, μi der Mittelwert von Klasse i und μ der Gesamtmittelwert aller Daten.

Optimierungsziel

LDA versucht, die Projektionsmatrix W zu finden, die das Fisher-Kriterium maximiert:

J(W) = |WT Sb W| / |WT Sw W|

Im Grunde geht's darum, das Verhältnis zwischen der Streuung zwischen den Klassen und der Streuung innerhalb der Klassen im projizierten Raum so hoch wie möglich zu machen. Die Lösung besteht darin, die Eigenvektoren der Matrix ^Sw-1Sb zu finden, die uns die Richtungen (lineare Diskriminanten) geben, die die Klassen am besten trennen.

So macht LDA dieses komplizierte Optimierungsproblem zu einer Eigenwertzerlegung, was esselbst für Datensätze mit mäßig hoher Dimension rechnerisch effizient macht.

Nachdem wir jetzt das Konzept und die mathematische Idee hinter LDA verstanden haben, schauen wir uns mal an, wie das Ganze in der Praxis funktioniert.

Praktische Anwendungen von LDA

LDA kann in vielen Bereichen eingesetzt werden, wo Klassifizierung und Dimensionsreduktion wichtig sind:

• Medizinische Diagnose: LDA wird in der medizinischen Bildgebung verwendet, um verschiedene Arten von Tumoren oder Anomalien zu klassifizieren. Es kann MRT-Scans analysieren, um zwischen gutartigen und bösartigen Geweben zu unterscheiden, indem es die auffälligsten Merkmale in den Bilddaten findet.
• Finanz- und Bank: Kreditbewertungssysteme nutzen LDA, um Kreditantragsteller in Risikokategorien einzuteilen. Durch die Analyse von Finanzkennzahlen wie Einkommen, Schuldenquote und Bonitätshistorie kann LDA dabei helfen, risikoreiche von risikoarmen Kreditnehmern zu unterscheiden.
• Bioinformatik-: Die Genexpressionsanalyse nutzt LDA, um verschiedene Krankheitszustände oder Reaktionen auf Behandlungen zu sortieren. Es hilft dabei, die Gene zu finden, die am wichtigsten sind, um gesunde von kranken Gewebeproben zu unterscheiden.
• Marketing und Kundensegmentierungs: Firmen nutzen LDA, um Kunden nach ihrem Kaufverhalten, demografischen Daten und Interaktionskennzahlen zu sortieren. Das ist super für gezielte Marketingaktionen und personalisierte Produktempfehlungen.
• Bilderkennungs: Gesichtserkennungssysteme nutzen LDA, um die Dimension von Gesichtsbildern zu reduzieren und gleichzeitig die Merkmale zu behalten, die für die Unterscheidung zwischen verschiedenen Personen am wichtigsten sind.
• Qualitätskontroll: In der Fertigung wird LDA genutzt, um Produkte anhand verschiedener Qualitätskennzahlen als fehlerhaft oder fehlerfrei einzustufen, was automatisierte Qualitätssicherungsprozesse ermöglicht.
• Spracherkennungs: LDA hilft bei der Klassifizierung von Phonemen, indem es die akustischen Merkmale identifiziert, die verschiedene Sprachlaute am besten unterscheiden, und so die Genauigkeit von Sprach-zu-Text-Systemen verbessert.
• Umweltüberwachungs: LDA wird verwendet, um Umweltbedingungen anhand von Sensordaten zu klassifizieren, z. B. um verschiedene Verschmutzungsgrade oder Wetterlagen zu unterscheiden.

Implementierung von LDA in Python

Schauen wir uns mal ein komplettes Beispiel für die Implementierung von LDA mit Python an. 

Wir nehmen den Datensatz „Seeds“, den du in der UCI-Bibliothek oder bei Kaggle runterladen kannst. Der Datensatzhat Messungen von Weizenkörnern von drei verschiedenen Weizensorten.

Schritt 1: Bibliotheken importieren und Daten laden

Zuerst importieren wir die benötigten Bibliotheken und laden unseren Datensatz:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score

# Load the seeds dataset
file_path = "seeds_dataset.txt"
column_names = ['area', 'perimeter', 'compactness', 'kernel_length',
               'kernel_width', 'asymmetry', 'groove_length', 'variety']

# Read the data with whitespace delimiter (space or tab)
seeds_df = pd.read_csv(file_path, sep='\s+', header=None, names=column_names)

print(f"Dataset shape: {seeds_df.shape}")
seeds_df.head()

Die ersten 5 Zeilen des geladenen Datensatzes siehst du unten:

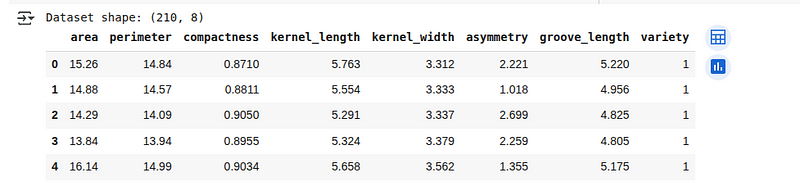Übersicht über den Datensatz „Seeds“. (Bild vom Autor)

Schritt 2: Datenvorverarbeitung

Schauen wir uns mal die Datenstruktur an und machen sie für die LDA-Analyse fertig:

# Check for missing values
print(f"Missing values: {seeds_df.isnull().sum().sum()}")

# Check class distribution
print("\nClass distribution:")
print(seeds_df['variety'].value_counts())

# Separate features and target
X = seeds_df.drop('variety', axis=1)
y = seeds_df['variety']

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
                                                   random_state=42, stratify=y)

# Standardize the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

Hier schauen wir, ob im Datensatz irgendwelche Werte fehlen und wie viele Beispiele zu jeder Kategorie gehören. Dann machen wir die Daten fertig, indem wir die Eingaben von den Labels trennen, sie in Trainings- und Testteile aufteilen und die Eingabewerte so anpassen, dass alle Merkmale auf einer ähnlichen Skala sind.

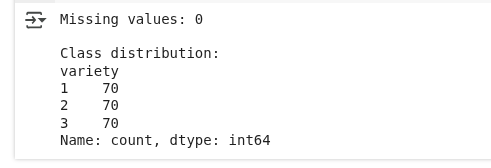
Datenvorverarbeitung. (Bild vom Autor)

Wir sehen, dass keine Werte fehlen und die Klassenverteilung gleichmäßig ist.

Schritt 3: LDA zur Reduzierung der Dimensionen anwenden

Jetzt werden wir LDA anwenden, um die Dimension unserer Daten zu reduzieren und gleichzeitig die Klassentrennbarkeit zu erhalten:

# Create and fit LDA model
lda = LinearDiscriminantAnalysis(n_components=2)
X_train_lda = lda.fit_transform(X_train_scaled, y_train)
X_test_lda = lda.transform(X_test_scaled)

# Print explained variance ratio
print("Explained variance ratio:", lda.explained_variance_ratio_)
print("Cumulative explained variance:", np.cumsum(lda.explained_variance_ratio_))

Wir entwickeln ein Modell, das die besten Wege findet, um die verschiedenen Kategorien in unseren Daten zu trennen. Indem wir die Daten auf zwei neue Merkmale reduzieren (da wir drei Kategorien haben), behalten wir die wichtigsten Muster, um sie voneinander zu unterscheiden.

Die Ausgabe sieht so aus:

LDA-Varianz-Ergebnisse. (Bild vom Autor)

Diese Ausgabe zeigt, wie viel von den klassenunterscheidenden Infos durch die beiden neuen Features erfasst werden, die LDA erstellt hat:

• Erklärte Varianzquote: Das heißt, die erste LDA-Komponente erfasst etwa 67,7 % der Infos, die man braucht, um die Klassen zu unterscheiden, während die zweite Komponente die restlichen 32,3 % erfasst.
• Kumulative erklärte Varianz: Zusammen fangen beide Teile 100 % der Infos ab, die die Klassen in den Originaldaten voneinander trennen. Das ist klar, weil wir drei Klassen haben und LDA höchstens zwei nützliche Richtungen gibt.

Schritt 4: Visualisiere die LDA-Transformation

Schauen wir mal, wie LDA unsere Daten umwandelt und die Klassen trennt:

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# Plot the first two original features
ax1.scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
           c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax1.set_xlabel('Area (standardized)')
ax1.set_ylabel('Perimeter (standardized)')
ax1.set_title('Original Feature Space (First Two Features)')
ax1.grid(True, alpha=0.3)

# Plot LDA-transformed data
scatter = ax2.scatter(X_train_lda[:, 0], X_train_lda[:, 1],
                     c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax2.set_xlabel('First Linear Discriminant')
ax2.set_ylabel('Second Linear Discriminant')
ax2.set_title('LDA-Transformed Space')
ax2.grid(True, alpha=0.3)

plt.colorbar(scatter, ax=ax2, label='Wheat Variety')
plt.tight_layout()
plt.show()

Der Code oben erstellt zwei nebeneinander angeordnete Diagramme, mit denen wir die Daten vor und nach der Anwendung der Dimensionsreduktionstechnik vergleichen können, wie unten zu sehen ist:

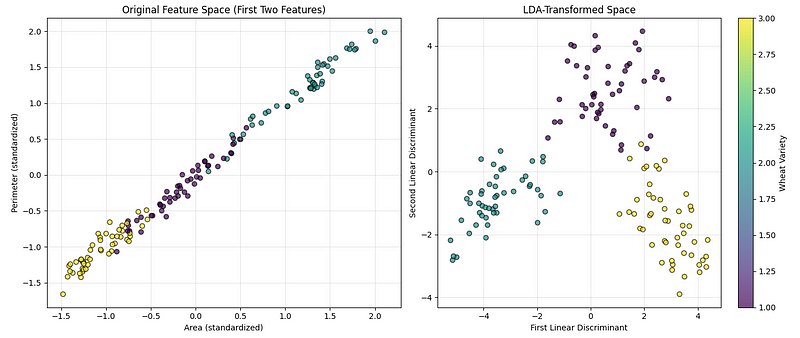LDA-Visualisierung. (Bild vom Autor)

Das erste Diagramm zeigt die Originaldaten mit zwei der gemessenen Merkmale (Fläche und Umfang), sodass wir sehen können, wie gut die Kategorien auf natürliche Weise voneinander getrennt sind. Das zweite Diagramm zeigt die Daten, nachdem sie so umgewandelt wurden, dass sie am besten helfen, die Kategorien zu trennen. Eine Farbleiste zeigt an, welche Farbe für welche Weizensorte steht.

Schritt 5: LDA für die Klassifizierung verwenden

LDA kann auch direkt als Klassifikator verwendet werden. 

Lass uns das umsetzen:

# Create LDA classifier
lda_classifier = LinearDiscriminantAnalysis()
lda_classifier.fit(X_train_scaled, y_train)

# Make predictions
y_pred = lda_classifier.predict(X_test_scaled)

# Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f"Classification Accuracy: {accuracy:.4f}")

# Print classification report
print("\nClassification Report:")
print(classification_report(y_test, y_pred))

Wir trainieren ein Modell, um anhand der Trainingsdaten die verschiedenen Weizensorten zu erkennen. Dann schauen wir, wie gut es bei neuen, unbekannten Beispielen funktioniert, indem wir die Gesamtgenauigkeit und die Vorhersagegenauigkeit für jede Kategorie checken.

Wir sehen die folgende Ausgabe:

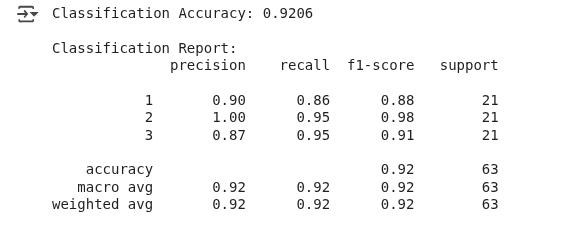
Ergebnisse der LDA-Klassifizierung. (Bild vom Autor)

Das Modell hat die Weizensorte in etwa 92 % der Fälle richtig vorhergesagt, was als gute Leistung angesehen werden kann. 

Dieses Beispiel zeigt, dass LDA zwar häufig zur Dimensionsreduktion eingesetzt wird, aber auch als Klassifikator dienen kann, indem es die Wahrscheinlichkeitsverteilung jeder Klasse modelliert und neue Daten der Klasse mit der höchsten Wahrscheinlichkeit zuordnet.

LDA im Vergleich zu PCA mit Codes und Visualisierungen

Die Hauptkomponentenanalyse ist eine weitere beliebte Technik zur Dimensionsreduktion, die die Richtungen der größten Abweichungen in den Daten findet. 

Lass uns unser vorheriges Beispiel erweitern, um LDA mit PCA zu vergleichen:

from sklearn.decomposition import PCA

# Apply PCA with 2 components
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
X_test_pca = pca.transform(X_test_scaled)

# Create comparison visualization
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# Plot PCA results
scatter1 = ax1.scatter(X_train_pca[:, 0], X_train_pca[:, 1],
                      c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax1.set_xlabel('First Principal Component')
ax1.set_ylabel('Second Principal Component')
ax1.set_title(f'PCA Transformation\nExplained Variance: {pca.explained_variance_ratio_.sum():.2%}')
ax1.grid(True, alpha=0.3)

# Plot LDA results
scatter2 = ax2.scatter(X_train_lda[:, 0], X_train_lda[:, 1],
                      c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax2.set_xlabel('First Linear Discriminant')
ax2.set_ylabel('Second Linear Discriminant')
ax2.set_title(f'LDA Transformation\nExplained Variance: {lda.explained_variance_ratio_.sum():.2%}')
ax2.grid(True, alpha=0.3)

plt.colorbar(scatter1, ax=ax1, label='Wheat Variety')
plt.colorbar(scatter2, ax=ax2, label='Wheat Variety')
plt.tight_layout()
plt.show()

Wir sehen die folgende Grafik:

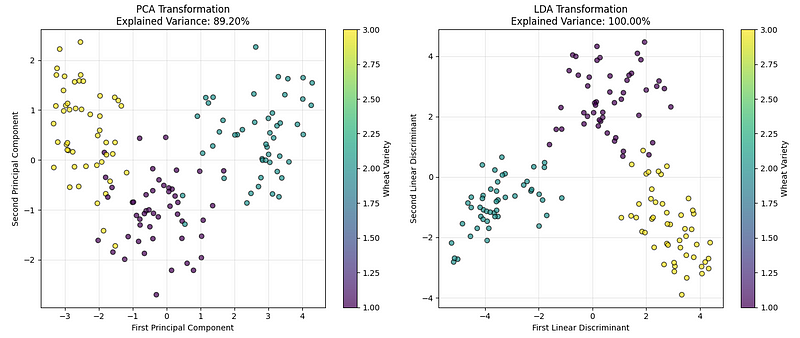LDA vs. PCA-Vergleich. (Bild vom Autor)

Das linke Diagramm zeigt die Daten mit PCA, die die Richtungen findet, die die meisten Gesamtabweichungen in den Daten erfassen. Das rechte Diagramm zeigt das Ergebnis der LDA, die die Richtungen findet, die die Weizenkategorien am besten trennen.

Aus unseren Implementierungsergebnissen und den erklärten Varianzwerten können wir schließen, dass beide gut funktionieren, aber bei Klassifizierungsproblemen wie diesen LDA normalerweise eine klarere Trennung zwischen Gruppen schafft.

Was LDA von anderen Techniken zur Dimensionsreduktion unterscheidet, ist, dass es überwacht wird. Während PCA nur die Abweichung in den Daten berücksichtigt, ohne auf Klassenbezeichnungen zu achten, nutzt LDA explizit Klasseninformationen, um die unterscheidungsfähigsten Richtungen zu finden. Das ist super, wenn man mit hochdimensionalen Daten arbeitet, bei denen die Trennbarkeit der Klassen wichtiger ist als die Erhaltung der Gesamtvarianz.

PCA kann also verwendet werden, wenn:

• Wir brauchen eine unbeaufsichtigte Reduzierung der Dimensionen.
• Klassenbezeichnungen sind nicht verfügbar oder nicht relevant.
• Wir wollen hochdimensionale Daten anschaulich darstellen.
• Wir müssen den Aufwand und die Komplexität der Berechnungen reduzieren.

Genauso können wir LDA verwenden, wenn:

• Wir haben Daten beschriftet und wollen die Klassentrennung optimieren.
• Die Anzahl der Proben pro Klasse ist ausreichend (normalerweise > 30).
• Wir brauchen sowohl eine Reduzierung der Dimensionen als auch eine Klassifizierung.
• Die Unterscheidung zwischen Klassen ist wichtiger als die Erhaltung der Gesamtvarianz.

Vor- und Nachteile von LDA

Wie jeder Algorithmus hat auch LDA seine Stärken und Grenzen, die wir beachten müssen, bevor wir ihn in unseren Projekten einsetzen.

Vorteile

• Vorteile des überwachten Lernens: Im Gegensatz zu PCA nutzt LDA Klassenlabel-Infos, um die besten Unterscheidungsmerkmale zu finden, was es für Klassifizierungsaufgaben besser macht.
• Dimensionsreduktion mit Klassifizierungs: Hat zwei Vorteile: Es macht alles kleiner und hat einen eingebauten Klassifizierer.
• Recheneffizienz: Braucht nur Eigenwertzerlegung, was es auch bei größeren Datensätzen schnell macht.
• Interpretierbarkeits: Die linearen Diskriminanten kann man als gewichtete Kombinationen der ursprünglichen Merkmale sehen.
• Super für Gaußsche Verteilungen: Es liefert den optimalen linearen Klassifikator, wenn Klassen Gaußschen Verteilungen mit gleichen Kovarianzmatrizen folgen.
• Keine Hyperparameter-Optimierung: Im Gegensatz zu vielen anderen Algorithmen für maschinelles Lernen gibt es bei LDA keine Hyperparameter, die für die grundlegende Implementierung angepasst werden müssen.

Nachteile

• Nur lineare Grenzen: Nicht lineare Beziehungen zwischen Merkmalen und Klassen können nicht erfasst werden.
• Gaußsche und gleiche Kovarianzannahme: Geht davon aus, dass jede Klasse einer multivariaten Gaußschen Verteilung folgt, was bei echten Daten vielleicht nicht stimmt, und dass alle Klassen die gleiche Kovarianzmatrix haben, was in der Praxis oft nicht der Fall ist.
• Begrenzte Komponenten: Kann maximal (n_classes — 1) unterscheidende Komponenten extrahieren, was für die Visualisierung bei Problemen mit mehreren Klassen nicht immer reicht.
• Empfindlich gegenüber Ausreißern und Multikollinearitätsproblemen: Die Mittelwert- und Kovarianzberechnungen reagieren empfindlich auf Ausreißer, und der Algorithmus kann bei stark korrelierten Merkmalen schlechte Ergebnisse liefern.
• Anforderungen an die Stichprobengröße: Man braucht genug Proben pro Klasse, um die Kovarianzmatrizen zuverlässig einschätzen zu können.

Wenn wir diese Vor- und Nachteile verstehen, können wir besser entscheiden, ob LDA der beste Algorithmus für das jeweilige Problem ist.

Fazit

In diesem Artikel ging es um die lineare Diskriminanzanalyse, eine überwachte Technik, die Dimensionsreduktion mit Klassifizierung kombiniert , indem sie das Verhältnis zwischen der Streuung innerhalb und außerhalb der Klassen maximiert.

Wir haben die mathematischen Grundlagen von LDA untersucht, sie mit Python umgesetzt und mit PCA verglichen, um zu verstehen, wann welche Technik am besten passt. Wir haben auch was über die praktischen Anwendungen von LDA gelernt und über die Vorteile und Grenzen gesprochen.

Wenn du dein Verständnis von LDA und verwandten Techniken des maschinellen Lernens vertiefen möchtest, solltest du dich für unseren Lernpfad „Supervised Machine Learning in Python“ anmelden, in dem du verschiedene Algorithmen und deren Implementierungen kennenlernst, oder für unseren Kurs „Dimensionality Reduction in Python“, um tiefer in überwachte und unüberwachte Techniken der Dimensionsreduktion einzutauchen.