Análise discriminante linear: Além da redução de dimensões

A análise discriminante linear (LDA) geralmente fica meio esquecida por um algoritmo mais popular, a análise de componentes principais (PCA), quando se trata de reduzir dimensões. Mas, a LDA tem algo que a PCA não tem: ela reduz as dimensões e, ao mesmo tempo, otimiza a separabilidade das classes.

Este tutorial vai te apresentar o LDA, a intuição matemática por trás dele e as aplicações práticas da técnica. Além disso, vamos implementar a LDA em um conjunto de dados, comparando-a com a PCA, e analisar suas vantagens e desvantagens, com o objetivo de fornecer tudo o que você precisa para começar a aplicar a LDA no seu próximo projeto.

Introdução à Análise Discriminante Linear (LDA)

LDA é uma técnica de redução de dimensões e classificação que parte do princípio de que classes diferentes geram dados com base em distribuições gaussianas diferentes. 

A LDA quer achar uma combinação linear de características que melhor separe essas classes. Isso maximiza a relação entre a dispersão entre classes e a dispersão dentro das classes. Em termos mais simples, ele tenta encontrar direções no espaço de características onde diferentes classes estão bem separadas umas das outras (alta dispersão entre classes), enquanto os pontos dentro da mesma classe estão próximos uns dos outros (baixa dispersão dentro da classe). 

Esse objetivo duplo torna a LDA super eficaz tanto pra reduzir dimensões quanto pra classificar.

A matemática por trás da LDA

Pra entender a matemática por trás da LDA, é preciso dividir o algoritmo em três partes principais: 

• dispersão dentro da classe, 
• dispersão entre classes, e
• objetivo de otimização.

Matriz de dispersão dentro da classe (Sw)

A matriz de dispersão dentro da classe mede o quanto os pontos de dados estão espalhados dentro de cada classe. 

Para cada classe i, calculamos a matriz de dispersão Si como:

Si = Σ(x - μi)(x - μi)T

Onde x é cada ponto de dados na classe i e μi é a média da classe i. A matriz de dispersão total dentro da classe é:

Sw = Σ Si (sum over all classes)

Matriz de dispersão entre classes (Sb)

A matriz de dispersão entre classes mede a distância entre as médias das classes e a média geral. É calculado assim:

Sb = Σ Ni(μi - μ)(μi - μ)T  

Onde Ni é o número de amostras na classe i, μi é a média da classe i e μ é a média geral de todos os dados.

Objetivo da otimização

A LDA tenta achar a matriz de projeção W que maximiza o critério de Fisher:

J(W) = |WT Sb W| / |WT Sw W|

Isso é basicamente maximizar a proporção entre a dispersão entre classes e a dispersão dentro das classes no espaço projetado. A solução é achar os vetores próprios da matriz ^Sw-1Sb, que nos dão as direções (discriminantes lineares) que melhor separam as classes.

Assim, o LDA transforma esse problema complicado de otimização em uma decomposição de valores próprios, tornando-oeficiente em termos de computação, mesmo para conjuntos de dados com dimensões moderadamente altas.

Agora que já entendemos o conceito e a intuição matemática por trás da LDA, vamos aprender sobre suas aplicações no mundo real.

Aplicações reais da LDA

A LDA tem aplicações em vários domínios onde é preciso classificar e reduzir a dimensionalidade:

• Diagnóstico médico: A LDA é usada em imagens médicas pra classificar diferentes tipos de tumores ou anormalidades. Ele consegue analisar exames de ressonância magnética pra diferenciar entre tecidos benignos e malignos, identificando as características mais distintas nos dados da imagem.
• Finanças e bancos: Os sistemas de pontuação de crédito usam a LDA para classificar os candidatos a empréstimos em categorias de risco. Ao analisar métricas financeiras como renda, relação dívida/renda e histórico de crédito, a LDA pode ajudar a separar os tomadores de empréstimos de alto risco dos de baixo risco.
• Bioinformática: A análise da expressão gênica usa a LDA para classificar diferentes estados da doença ou respostas ao tratamento. Isso ajuda a descobrir quais genes são mais importantes pra diferenciar amostras de tecido saudável e doente.
• Marketing e segmentação de clientes: As empresas usam a LDA pra segmentar os clientes com base no comportamento de compra, dados demográficos e métricas de engajamento. Isso é útil em campanhas de marketing direcionadas e recomendações personalizadas de produtos.
• Reconhecimento de imagem: Os sistemas de reconhecimento facial usam LDA pra reduzir a dimensão das imagens faciais, mantendo as características mais importantes pra diferenciar as pessoas.
• Controle de qualidade: As indústrias de manufatura usam a LDA pra classificar produtos como defeituosos ou não defeituosos com base em várias métricas de qualidade, o que permite processos automatizados de garantia de qualidade.
• e de reconhecimento de voz: A LDA ajuda na classificação de fonemas, identificando as características acústicas que melhor distinguem os diferentes sons da fala, melhorando a precisão dos sistemas de conversão de voz em texto.
• Monitoramento ambiental: A LDA é usada pra classificar condições ambientais com base em dados de sensores, como distinguir entre diferentes níveis de poluição ou padrões climáticos.

Implementação do LDA em Python

Vamos ver um exemplo completo de como implementar LDA usando Python. 

Vamos usar o conjunto de dados Seeds, que pode ser baixado da biblioteca da UCI e também do Kaggle. O conjunto de dadostem medidas de grãos de trigo de três variedades diferentes.

Passo 1: Importar bibliotecas e carregar os dados

Primeiro, vamos importar as bibliotecas necessárias e carregar nosso conjunto de dados:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score

# Load the seeds dataset
file_path = "seeds_dataset.txt"
column_names = ['area', 'perimeter', 'compactness', 'kernel_length',
               'kernel_width', 'asymmetry', 'groove_length', 'variety']

# Read the data with whitespace delimiter (space or tab)
seeds_df = pd.read_csv(file_path, sep='\s+', header=None, names=column_names)

print(f"Dataset shape: {seeds_df.shape}")
seeds_df.head()

Vamos ver as primeiras 5 linhas do conjunto de dados carregado abaixo:

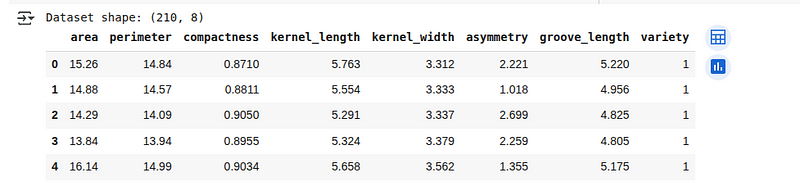Visão geral do conjunto de dados Seeds. (Imagem do autor)

Passo 2: Pré-processamento de dados

Vamos dar uma olhada na estrutura dos dados e prepará-los para a análise LDA:

# Check for missing values
print(f"Missing values: {seeds_df.isnull().sum().sum()}")

# Check class distribution
print("\nClass distribution:")
print(seeds_df['variety'].value_counts())

# Separate features and target
X = seeds_df.drop('variety', axis=1)
y = seeds_df['variety']

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
                                                   random_state=42, stratify=y)

# Standardize the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

Aqui, estamos verificando se o conjunto de dados tem algum valor faltando e vendo quantos exemplos pertencem a cada categoria. Depois, a gente prepara os dados separando as entradas dos rótulos, dividindo em partes de treinamento e teste e padronizando os valores de entrada pra que todas as características fiquem numa escala parecida.

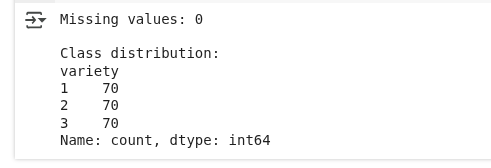
Pré-processamento dos dados. (Imagem do autor)

Vemos que não tem nenhum valor faltando e que a distribuição das classes tá igual.

Passo 3: Usando LDA pra reduzir dimensões

Agora vamos usar o LDA pra reduzir a dimensão dos nossos dados, mantendo a separabilidade das classes:

# Create and fit LDA model
lda = LinearDiscriminantAnalysis(n_components=2)
X_train_lda = lda.fit_transform(X_train_scaled, y_train)
X_test_lda = lda.transform(X_test_scaled)

# Print explained variance ratio
print("Explained variance ratio:", lda.explained_variance_ratio_)
print("Cumulative explained variance:", np.cumsum(lda.explained_variance_ratio_))

A gente tá criando um modelo que encontra as melhores direções pra separar as diferentes categorias nos nossos dados. Ao reduzir os dados a duas novas características (já que temos três categorias), a gente mantém os padrões mais importantes para diferenciar entre elas.

O resultado é assim:

Resultados da variância LDA. (Imagem do autor)

Essa saída mostra quanto das informações que separam as classes são capturadas pelos dois novos recursos criados pelo LDA:

• Índice de variação explicada: Isso quer dizer que o primeiro componente LDA pega cerca de 67,7% das informações necessárias pra diferenciar as classes, enquanto o segundo componente pega os 32,3% restantes.
• Variação explicada acumulada: Juntos, os dois componentes pegam 100% das informações que separam as classes nos dados originais. Isso é esperado, já que temos 3 classes e o LDA dá no máximo 2 direções úteis.

Passo 4: Visualize a transformação LDA

Vamos ver como o LDA transforma nossos dados e separa as classes:

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# Plot the first two original features
ax1.scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
           c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax1.set_xlabel('Area (standardized)')
ax1.set_ylabel('Perimeter (standardized)')
ax1.set_title('Original Feature Space (First Two Features)')
ax1.grid(True, alpha=0.3)

# Plot LDA-transformed data
scatter = ax2.scatter(X_train_lda[:, 0], X_train_lda[:, 1],
                     c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax2.set_xlabel('First Linear Discriminant')
ax2.set_ylabel('Second Linear Discriminant')
ax2.set_title('LDA-Transformed Space')
ax2.grid(True, alpha=0.3)

plt.colorbar(scatter, ax=ax2, label='Wheat Variety')
plt.tight_layout()
plt.show()

O código acima cria dois gráficos lado a lado pra nos ajudar a comparar como os dados ficam antes e depois de usar a técnica de redução de dimensionalidade, como dá pra ver abaixo:

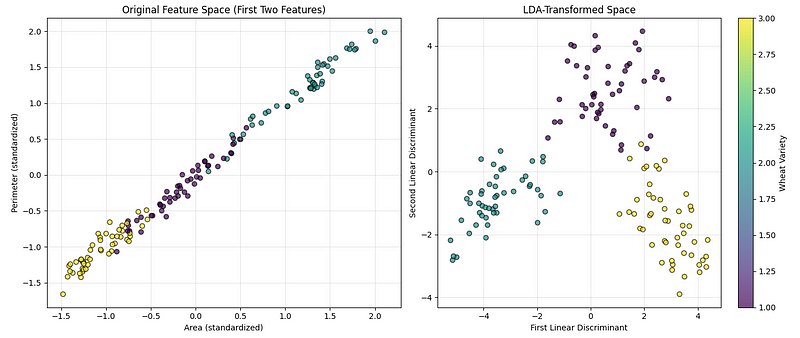Visualização LDA. (Imagem do autor)

O primeiro gráfico mostra os dados originais usando duas das características medidas (área e perímetro), para que possamos ver como as categorias estão bem separadas naturalmente. O segundo gráfico mostra os dados depois de transformados nas direções mais informativas para separar as categorias. Uma barra colorida foi adicionada para mostrar qual cor representa cada tipo de trigo.

Passo 5: Use LDA para classificação

A LDA também pode ser usada diretamente como classificador. 

Vamos implementar:

# Create LDA classifier
lda_classifier = LinearDiscriminantAnalysis()
lda_classifier.fit(X_train_scaled, y_train)

# Make predictions
y_pred = lda_classifier.predict(X_test_scaled)

# Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f"Classification Accuracy: {accuracy:.4f}")

# Print classification report
print("\nClassification Report:")
print(classification_report(y_test, y_pred))

Estamos treinando um modelo para reconhecer as diferentes categorias de trigo com base nos dados de treinamento. Depois, a gente testa como ele se sai em exemplos novos e desconhecidos, verificando a precisão geral e como ele prevê cada categoria.

A gente vê o seguinte resultado:

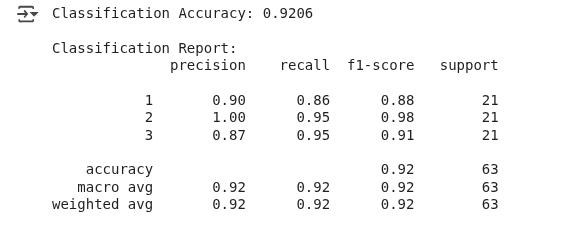
Resultados da classificação LDA. (Imagem do autor)

O modelo acertou o tipo de trigo em cerca de 92% das vezes, o que é um bom resultado. 

Esse exemplo mostrou que, embora o LDA seja mais usado pra reduzir dimensões, ele também pode ser um classificador, modelando a distribuição de probabilidade de cada classe e colocando novos dados na classe com maior chance de ser a certa.

Comparando LDA vs. PCA com códigos e visualizações

A Análise de Componentes Principais é outra técnica popular de redução de dimensionalidade que encontra as direções de maior variação nos dados. 

Vamos dar uma olhada no exemplo anterior pra comparar LDA com PCA:

importado de sklearn.decomposition PCA

# Apply PCA with 2 components
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
X_test_pca = pca.transform(X_test_scaled)

# Create comparison visualization
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# Plot PCA results
scatter1 = ax1.scatter(X_train_pca[:, 0], X_train_pca[:, 1],
                      c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax1.set_xlabel('First Principal Component')
ax1.set_ylabel('Second Principal Component')
ax1.set_title(f'PCA Transformation\nExplained Variance: {pca.explained_variance_ratio_.sum():.2%}')
ax1.grid(True, alpha=0.3)

# Plot LDA results
scatter2 = ax2.scatter(X_train_lda[:, 0], X_train_lda[:, 1],
                      c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax2.set_xlabel('First Linear Discriminant')
ax2.set_ylabel('Second Linear Discriminant')
ax2.set_title(f'LDA Transformation\nExplained Variance: {lda.explained_variance_ratio_.sum():.2%}')
ax2.grid(True, alpha=0.3)

plt.colorbar(scatter1, ax=ax1, label='Wheat Variety')
plt.colorbar(scatter2, ax=ax2, label='Wheat Variety')
plt.tight_layout()
plt.show()

A gente vê o seguinte gráfico:

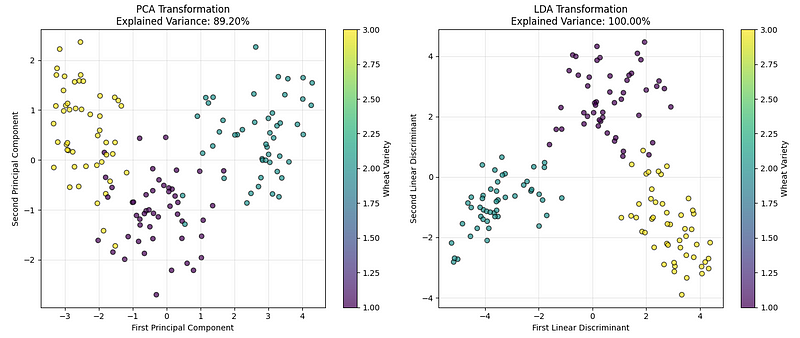LDA vs. Comparação PCA. (Imagem do autor)

O gráfico da esquerda mostra os dados usando PCA, que encontra as direções que capturam a maior variação geral nos dados. O gráfico da direita mostra o resultado da LDA, que encontra as direções que melhor separam as categorias de trigo.

Com base nos resultados da nossa implementação e nos valores de variância explicados, podemos concluir que, embora ambos tenham um bom desempenho, para problemas de classificação como este, o LDA geralmente cria uma separação mais clara entre os grupos.

O que faz o LDA ser diferente de outras técnicas de redução de dimensões é que ele é supervisionado. Enquanto a PCA só olha para a variação nos dados sem se importar com os rótulos das classes, a LDA usa explicitamente as informações das classes para encontrar as direções mais discriminatórias. Isso é ideal quando se lida com dados de alta dimensão, onde a separabilidade das classes é mais importante do que preservar a variância geral.

Então, a PCA pode ser usada quando:

• Precisamos de redução de dimensionalidade sem supervisão.
• Os rótulos de classe não estão disponíveis ou não fazem sentido
• Queremos visualizar dados de alta dimensão.
• Precisamos reduzir o ruído e a complexidade computacional.

Da mesma forma, podemos usar LDA quando:

• Temos dados rotulados e queremos maximizar a separação entre classes.
• O número de amostras por classe é suficiente (geralmente > 30).
• Precisamos tanto de redução de dimensões quanto de classificação.
• A discriminação de classe é mais importante do que preservar a variação geral.

Prós e contras da LDA

Como qualquer algoritmo, o LDA tem seus pontos fortes e fracos que a gente precisa ter em mente antes de usar nos nossos projetos.

Vantagens

• Vantagem da aprendizagem supervisionada: Diferente da PCA, a LDA usa informações de rótulos de classe pra achar as características mais distintas, o que a torna mais eficaz pra tarefas de classificação.
• Redução da dimensionalidade com classificação: Tem a dupla função de reduzir as dimensões e fornecer um classificador integrado.
• Eficiência computacional: Só precisa da decomposição em valores próprios, o que torna tudo mais rápido, mesmo com conjuntos de dados grandes.
• Interpretabilidade: Os discriminantes lineares podem ser interpretados como combinações ponderadas das características originais.
• Ótimo para distribuições gaussianas: Ele fornece o classificador linear ideal quando as classes seguem distribuições gaussianas com matrizes de covariância iguais.
• Sem ajuste de hiperparâmetros: Diferente de muitos algoritmos de machine learning, o LDA não tem hiperparâmetros pra ajustar na implementação básica.

Desvantagens

• Limites lineares apenas: Não dá pra capturar relações não lineares entre características e classes.
• Suposição de covariância gaussiana e igual: Pensa que cada classe segue uma distribuição gaussiana multivariada, o que pode não ser verdade para dados reais, e acha que todas as classes têm a mesma matriz de covariância, o que muitas vezes não é verdade na prática.
• Componentes limitados: Pode extrair no máximo (n_classes — 1) componentes discriminantes, o que pode ser insuficiente para visualização em problemas com várias classes.
• Sensível a valores atípicos e problemas de multicolinearidade: Os cálculos da média e da covariância são sensíveis a valores atípicos, e o algoritmo pode funcionar mal quando as características estão muito correlacionadas.
• Requisitos de tamanho da amostra: Precisa de amostras suficientes por classe pra calcular as matrizes de covariância de forma confiável.

Entender essas vantagens e desvantagens ajuda a gente a decidir se o LDA é o melhor algoritmo pra resolver o problema que a gente tá enfrentando.

Conclusão

Este artigo apresentou a análise discriminante linear, uma técnica supervisionada que combina a redução da dimensionalidade com a classificação , maximizando a proporção entre a dispersão entre classes e a dispersão dentro das classes.

A gente explorou os fundamentos matemáticos da LDA, implementou usando Python e comparou com a PCA pra entender quando cada técnica é mais adequada. Também aprendemos sobre as aplicações reais da LDA e discutimos suas vantagens e limitações.

Para entender melhor o LDA e as técnicas de machine learning relacionadas, dá uma olhada no nosso programa Supervised Machine Learning in Python, onde você vai aprender vários algoritmos e como usá-los, ou no nosso curso Dimensionality Reduction in Python para se aprofundar nas técnicas de redução de dimensões supervisionadas e não supervisionadas.