Análisis discriminante lineal: Más allá de la reducción de dimensiones

El análisis discriminante lineal (LDA) suele quedar eclipsado por un algoritmo más popular, el análisis de componentes principales (PCA), cuando se trata de la reducción de la dimensionalidad. Sin embargo, el LDA ofrece algo único que el PCA no puede ofrecer: reduce las dimensiones y optimiza la separabilidad de las clases al mismo tiempo.

Este tutorial te presentará LDA, la intuición matemática que hay detrás y las aplicaciones prácticas de esta técnica. Además, implementaremos LDA en un conjunto de datos, comparándolo con PCA, y analizaremos sus ventajas y desventajas, con el objetivo de proporcionar todo lo necesario para comenzar a aplicar LDA en tu próximo proyecto.

Introducción al análisis discriminante lineal (LDA)

El LDA es una técnica de reducción de dimensiones y clasificación que parte de la hipótesis de que las diferentes clases generan datos basados en diferentes distribuciones gaussianas. 

El LDA tiene como objetivo encontrar una combinación lineal de características que separe mejor estas clases. Maximiza la relación entre la dispersión entre clases y la dispersión dentro de una misma clase. En términos más sencillos, intenta encontrar direcciones en el espacio de características donde las diferentes clases estén muy separadas entre sí (alta dispersión entre clases), mientras que los puntos dentro de la misma clase estén muy próximos entre sí (baja dispersión dentro de la clase). 

Este doble objetivo hace que el LDA sea especialmente eficaz tanto para tareas de reducción de dimensionalidad como para tareas de clasificación.

Las matemáticas detrás del LDA

Para comprender las matemáticas que hay detrás del LDA, es necesario desglosar el algoritmo en tres componentes clave: 

• dispersión dentro de la clase, 
• dispersión entre clases, y
• objetivo de optimización.

Matriz de dispersión dentro de la clase (Sw)

La matriz de dispersión dentro de la clase mide cuán dispersos están los puntos de datos dentro de cada clase. 

Para cada clase i, calculamos la matriz de dispersión Si como:

Si = Σ(x - μi)(x - μi)T

Donde x representa cada punto de datos en la clase i, y μi es la media de la clase i. La matriz de dispersión total dentro de la clase es:

Sw = Σ Si (sum over all classes)

Matriz de dispersión entre clases (Sb)

La matriz de dispersión entre clases mide la distancia entre las medias de las clases y la media global. Se calcula de la siguiente manera:

Sb = Σ Ni(μi - μ)(μi - μ)T  

Donde Ni es el número de muestras en la clase i, μi es la media de la clase i y μ es la media global de todos los datos.

Objetivo de optimización

El LDA busca encontrar la matriz de proyección W que maximice el criterio de Fisher:

J(W) = |WT Sb W| / |WT Sw W|

Esto consiste básicamente en maximizar la relación entre la dispersión entre clases y la dispersión dentro de una misma clase en el espacio proyectado. La solución consiste en encontrar los vectores propios de la matriz ^Sw-1Sb, lo que nos da las direcciones (discriminantes lineales) que mejor separan las clases.

De este modo, el LDA reduce este complejo problema de optimización a una descomposición en valores propios, lo que lo hacecomputacionalmente eficiente incluso para conjuntos de datos de dimensión moderadamente alta.

Ahora que hemos entendido el concepto y la intuición matemática detrás del LDA, aprendamos sobre sus aplicaciones en el mundo real.

Aplicaciones reales del LDA

El LDA tiene aplicaciones en varios ámbitos en los que se requiere clasificación y reducción de la dimensionalidad:

• Diagnóstico médico: El LDA se utiliza en imágenes médicas para clasificar diferentes tipos de tumores o anomalías. Puede analizar resonancias magnéticas para distinguir entre tejidos benignos y malignos mediante la identificación de las características más discriminatorias en los datos de la imagen.
• Finanzas y banca: Los sistemas de puntuación crediticia utilizan el LDA para clasificar a los solicitantes de préstamos en categorías de riesgo. Mediante el análisis de indicadores financieros como los ingresos, la relación entre deuda e ingresos y el historial crediticio, LDA puede ayudar a diferenciar a los prestatarios de alto riesgo de los de bajo riesgo.
• Bioinformática: El análisis de la expresión génica utiliza el LDA para clasificar diferentes estados de la enfermedad o respuestas al tratamiento. Ayuda a identificar qué genes son más importantes para distinguir entre muestras de tejido sano y enfermo.
• Marketing y segmentación de clientes: Las empresas utilizan el LDA para segmentar a los clientes en función de su comportamiento de compra, datos demográficos y métricas de interacción. Esto resulta útil en campañas de marketing dirigidas y recomendaciones personalizadas de productos.
• Reconocimiento de imágenes: Los sistemas de reconocimiento facial utilizan el LDA para reducir la dimensionalidad de las imágenes faciales, conservando al mismo tiempo las características más importantes para distinguir entre diferentes individuos.
• Control de calidad: Las industrias manufactureras aplican el LDA para clasificar los productos como defectuosos o no defectuosos en función de diversos parámetros de calidad, lo que permite automatizar los procesos de control de calidad.
• : reconocimiento de voz. El LDA ayuda en la clasificación de fonemas identificando las características acústicas que mejor distinguen entre los diferentes sonidos del habla, mejorando la precisión de los sistemas de conversión de voz a texto.
• : El LDA se utiliza para clasificar las condiciones ambientales basándose en datos de sensores, como por ejemplo, distinguir entre diferentes niveles de contaminación o patrones meteorológicos.

Implementación de LDA en Python

Veamos un ejemplo completo de implementación de LDA con Python. 

Utilizaremos el conjunto de datos Seeds, que se puede descargar desde la biblioteca de la UCI y desde Kaggle. El conjunto de datoscontiene mediciones de granos de trigo pertenecientes a tres variedades diferentes de trigo.

Paso 1: Importa las bibliotecas y carga los datos.

Primero, importaremos las bibliotecas necesarias y cargaremos nuestro conjunto de datos:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score

# Load the seeds dataset
file_path = "seeds_dataset.txt"
column_names = ['area', 'perimeter', 'compactness', 'kernel_length',
               'kernel_width', 'asymmetry', 'groove_length', 'variety']

# Read the data with whitespace delimiter (space or tab)
seeds_df = pd.read_csv(file_path, sep='\s+', header=None, names=column_names)

print(f"Dataset shape: {seeds_df.shape}")
seeds_df.head()

A continuación, veremos las primeras 5 líneas del conjunto de datos cargado:

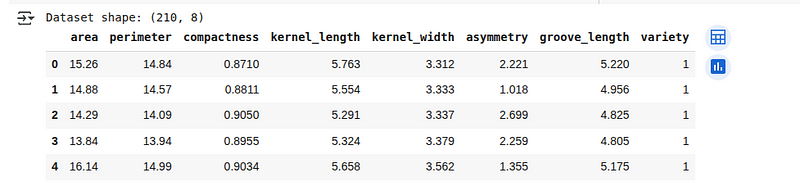Descripción general del conjunto de datos Seeds. (Imagen del autor)

Paso 2: Preprocesamiento de datos

Exploremos la estructura de datos y preparémosla para el análisis LDA:

# Check for missing values
print(f"Missing values: {seeds_df.isnull().sum().sum()}")

# Check class distribution
print("\nClass distribution:")
print(seeds_df['variety'].value_counts())

# Separate features and target
X = seeds_df.drop('variety', axis=1)
y = seeds_df['variety']

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
                                                   random_state=42, stratify=y)

# Standardize the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

Aquí, estamos comprobando si el conjunto de datos tiene algún valor perdido y examinando cuántos ejemplos pertenecen a cada categoría. A continuación, preparamos los datos separando las entradas de las etiquetas, dividiéndolos en partes de entrenamiento y prueba, y estandarizando los valores de entrada para que todas las características estén en una escala similar.

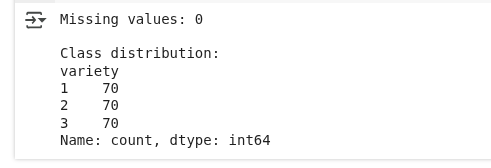
Preprocesamiento de datos. (Imagen del autor)

Vemos que no hay valores perdidos y que la distribución de clases es igual.

Paso 3: Aplicación del LDA para la reducción de la dimensionalidad

Ahora aplicaremos LDA para reducir la dimensionalidad de nuestros datos y preservar la separabilidad de las clases:

# Create and fit LDA model
lda = LinearDiscriminantAnalysis(n_components=2)
X_train_lda = lda.fit_transform(X_train_scaled, y_train)
X_test_lda = lda.transform(X_test_scaled)

# Print explained variance ratio
print("Explained variance ratio:", lda.explained_variance_ratio_)
print("Cumulative explained variance:", np.cumsum(lda.explained_variance_ratio_))

Estamos creando un modelo que encuentra las mejores direcciones para separar las diferentes categorías de nuestros datos. Al reducir los datos a dos nuevas características (ya que tenemos tres categorías), conservamos los patrones más importantes para distinguirlos.

El resultado es el siguiente:

Resultados de la varianza LDA. (Imagen del autor)

Este resultado muestra cuánta información que separa las clases es capturada por las dos nuevas características creadas por LDA:

• Índice de varianza explicada: Esto significa que el primer componente LDA captura aproximadamente el 67,7 % de la información necesaria para distinguir entre las clases, mientras que el segundo componente captura el 32,3 % restante.
• Varianza acumulada explicada: Juntos, ambos componentes capturan el 100 % de la información que separa las clases en los datos originales. Esto es de esperar, ya que tenemos tres clases y el LDA proporciona como máximo dos direcciones útiles.

Paso 4: Visualiza la transformación LDA

Visualicemos cómo LDA transforma nuestros datos y separa las clases:

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# Plot the first two original features
ax1.scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
           c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax1.set_xlabel('Area (standardized)')
ax1.set_ylabel('Perimeter (standardized)')
ax1.set_title('Original Feature Space (First Two Features)')
ax1.grid(True, alpha=0.3)

# Plot LDA-transformed data
scatter = ax2.scatter(X_train_lda[:, 0], X_train_lda[:, 1],
                     c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax2.set_xlabel('First Linear Discriminant')
ax2.set_ylabel('Second Linear Discriminant')
ax2.set_title('LDA-Transformed Space')
ax2.grid(True, alpha=0.3)

plt.colorbar(scatter, ax=ax2, label='Wheat Variety')
plt.tight_layout()
plt.show()

El código anterior crea dos gráficos uno al lado del otro para ayudarnos a comparar cómo se ven los datos antes y después de aplicar la técnica de reducción de dimensionalidad, como se ve a continuación:

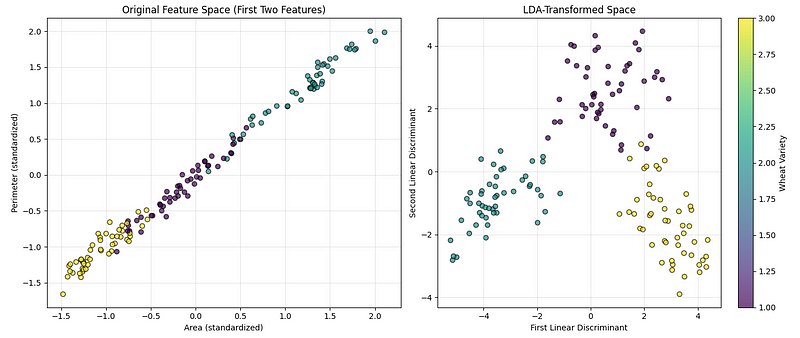Visualización LDA. (Imagen del autor)

El primer gráfico muestra los datos originales utilizando dos de las características medidas (área y perímetro), de modo que podemos ver cómo se separan las categorías de forma natural. El segundo gráfico muestra los datos después de transformarlos en las direcciones más informativas para separar las categorías. Se añade una barra de colores para indicar qué color representa cada tipo de trigo.

Paso 5: Utiliza LDA para la clasificación.

El LDA también se puede utilizar directamente como clasificador. 

Implementémoslo:

# Create LDA classifier
lda_classifier = LinearDiscriminantAnalysis()
lda_classifier.fit(X_train_scaled, y_train)

# Make predictions
y_pred = lda_classifier.predict(X_test_scaled)

# Calculate accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f"Classification Accuracy: {accuracy:.4f}")

# Print classification report
print("\nClassification Report:")
print(classification_report(y_test, y_pred))

Estamos entrenando un modelo para reconocer las diferentes categorías de trigo basándonos en los datos de entrenamiento. A continuación, probamos su rendimiento con ejemplos nuevos y desconocidos, comprobando su precisión general y su capacidad para predecir cada categoría.

Vemos el siguiente resultado:

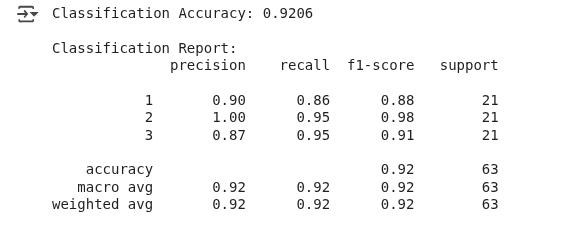
Resultados de la clasificación LDA. (Imagen del autor)

El modelo predijo correctamente el tipo de trigo en aproximadamente el 92 % de los casos, lo que puede considerarse un buen rendimiento. 

Este ejemplo ha demostrado que, aunque el LDA se utiliza habitualmente para la reducción de la dimensionalidad, también puede actuar como clasificador modelando la distribución de probabilidad de cada clase y asignando los nuevos datos a la clase con mayor probabilidad.

Comparación entre LDA y PCA con códigos y visualizaciones

El análisis de componentes principales es otra técnica popular de reducción de dimensionalidad que encuentra las direcciones de máxima varianza en los datos. 

Ampliemos nuestro ejemplo anterior para comparar LDA con PCA:

de sklearn.decomposition import PCA

# Apply PCA with 2 components
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
X_test_pca = pca.transform(X_test_scaled)

# Create comparison visualization
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# Plot PCA results
scatter1 = ax1.scatter(X_train_pca[:, 0], X_train_pca[:, 1],
                      c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax1.set_xlabel('First Principal Component')
ax1.set_ylabel('Second Principal Component')
ax1.set_title(f'PCA Transformation\nExplained Variance: {pca.explained_variance_ratio_.sum():.2%}')
ax1.grid(True, alpha=0.3)

# Plot LDA results
scatter2 = ax2.scatter(X_train_lda[:, 0], X_train_lda[:, 1],
                      c=y_train, cmap='viridis', alpha=0.7, edgecolor='k')
ax2.set_xlabel('First Linear Discriminant')
ax2.set_ylabel('Second Linear Discriminant')
ax2.set_title(f'LDA Transformation\nExplained Variance: {lda.explained_variance_ratio_.sum():.2%}')
ax2.grid(True, alpha=0.3)

plt.colorbar(scatter1, ax=ax1, label='Wheat Variety')
plt.colorbar(scatter2, ax=ax2, label='Wheat Variety')
plt.tight_layout()
plt.show()

Vemos el siguiente gráfico:

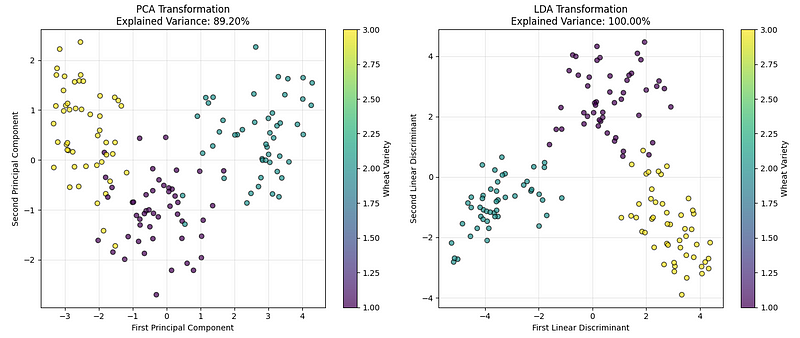LDA frente a Comparación PCA. (Imagen del autor)

El gráfico de la izquierda muestra los datos utilizando el PCA, que encuentra las direcciones que capturan la mayor variación global en los datos. El gráfico de la derecha muestra el resultado del LDA, que encuentra las direcciones que mejor separan las categorías de trigo.

Basándonos en los resultados de nuestra implementación y en los valores de varianza explicados, podemos concluir que, aunque ambos funcionan bien, para problemas de clasificación como este, LDA suele crear una separación más clara entre los grupos.

Lo que distingue a LDA de otras técnicas de reducción de dimensionalidad es su naturaleza supervisada. Mientras que el PCA solo tiene en cuenta la varianza en los datos sin tener en cuenta las etiquetas de clase, el LDA utiliza explícitamente la información de clase para encontrar las direcciones más discriminatorias. Esto es ideal cuando se trabaja con datos de alta dimensión, en los que la separabilidad de clases es más importante que preservar la varianza global.

Por lo tanto, el PCA se puede utilizar cuando:

• Necesitamos una reducción de la dimensionalidad sin supervisión.
• Las etiquetas de clase no están disponibles o no son relevantes.
• Queremos visualizar datos de alta dimensión.
• Necesitamos reducir el ruido y la complejidad computacional.

Del mismo modo, podemos utilizar LDA cuando:

• Tenemos datos etiquetados y queremos maximizar la separación entre clases.
• El número de muestras por clase es suficiente (por lo general, más de 30).
• Necesitamos tanto la reducción de la dimensionalidad como la clasificación.
• La discriminación de clase es más importante que preservar la varianza general.

Ventajas y desventajas del LDA

Como cualquier algoritmo, LDA tiene sus puntos fuertes y sus limitaciones, que debemos tener en cuenta antes de aplicarlo en nuestros proyectos.

Ventajas

• Ventajas del aprendizaje supervisado: A diferencia del PCA, el LDA utiliza información de etiquetas de clase para encontrar las características más discriminatorias, lo que lo hace más eficaz para tareas de clasificación.
• Reducción de la dimensionalidad con clasificación: Tiene una doble función: reduce las dimensiones y proporciona un clasificador integrado.
• Eficiencia computacional: Solo requiere la descomposición en valores propios, lo que lo hace rápido incluso para conjuntos de datos de tamaño moderado.
• Interpretabilidad: Los discriminantes lineales pueden interpretarse como combinaciones ponderadas de características originales.
• Óptimo para distribuciones gaussianas: Proporciona el clasificador lineal óptimo cuando las clases siguen distribuciones gaussianas con matrices de covarianza iguales.
• Sin ajuste de hiperparámetros: A diferencia de muchos algoritmos de machine learning, LDA no tiene hiperparámetros que ajustar para su implementación básica.

Desventajas

• Límites lineales únicamente: No se pueden capturar relaciones no lineales entre características y clases.
• Supuesto de covarianza gaussiana e igual: Asume que cada clase sigue una distribución gaussiana multivariante, lo que puede no ser válido para datos reales, y asume que todas las clases tienen la misma matriz de covarianza, lo que a menudo se incumple en la práctica.
• Componentes limitados: Puede extraer como máximo (n_classes — 1) componentes discriminantes, lo que puede ser insuficiente para la visualización en problemas multiclase.
• Sensible a valores atípicos y problemas de multicolinealidad: Los cálculos de la media y la covarianza son sensibles a los valores atípicos, y el algoritmo puede funcionar mal cuando las características están muy correlacionadas.
• Requisitos del tamaño de la muestra: Requiere muestras suficientes por clase para estimar las matrices de covarianza de forma fiable.

Comprender estas ventajas e inconvenientes nos ayuda a determinar si el LDA es el mejor algoritmo para aplicar al problema que nos ocupa.

Conclusión

Este artículo presentó el análisis discriminante lineal, una técnica supervisada que combina la reducción de la dimensionalidad con la clasificación , maximizando la relación entre la dispersión entre clases y la dispersión dentro de las clases.

Exploramos los fundamentos matemáticos del LDA, lo implementamos utilizando Python y lo comparamos con el PCA para comprender cuándo es más adecuado cada método. También aprendimos sobre las aplicaciones prácticas del LDA y debatimos sus ventajas y limitaciones.

Para profundizar en tu comprensión del LDA y las técnicas de machine learning relacionadas, considera la posibilidad de inscribirte en nuestro programa Supervised Machine Learning in Python, donde dominarás varios algoritmos y sus implementaciones, o en nuestro curso Dimensionality Reduction in Python para profundizar en las técnicas de reducción de dimensiones supervisadas y no supervisadas.