Lineare Programmierung: Lösung realer Optimierungsprobleme

Betriebsleiter haben immer wieder mit dem gleichen Problem zu kämpfen: zu viele Entscheidungen, zu viele Einschränkungen und keine klare Lösung in Sicht. Ein Vertriebsnetz muss die Kraftstoffkosten auf Dutzenden von Routen so niedrig wie möglich halten und dabei Lieferzeiten, Fahrzeugkapazitäten und Fahrpläne der Fahrer beachten.

Diese beiden Probleme haben eine ähnliche mathematische Struktur. Wenn deine Ziele und Einschränkungen als lineare Beziehungen ausgedrückt werden können, hast du es mit einem linearen Programmierungsproblem zu tun. Lineare Programmierung ist uns wichtig, weil sie optimale Lösungen findet, wenn man mit begrenzten Ressourcen und konkurrierenden Anforderungen arbeitet.

Was die lineare Programmierung so stark macht, ist ihre Garantie: Wenn es eine machbare Lösung gibt, findet der Algorithmus die beste. Klar, echte Anwendungen passen selten perfekt zu den Beispielen aus den Lehrbüchern, aber wenn du das Grundgerüst verstehst, kannst du besser erkennen, wann Optimierung das Rätselraten ersetzen kann.

Dieser Leitfaden führt dich von den Grundlagen bis hin zu funktionierenden Python-Implementierungen. Wir fangen mit einfachen Problemen mit zwei Variablen an, die du dir geometrisch vorstellen kannst, und arbeiten uns dann zu komplexen Szenarien vor, die algorithmische Lösungen brauchen. Du wirst sowohl die mathematische Theorie hinter der Optimierung als auch die praktischen Fähigkeiten verstehen, um Lösungen selbst umzusetzen.

Was ist lineare Programmierung?

Lineare Programmierung optimiert eine lineare Zielfunktion, die linearen Einschränkungen unterliegt. Bei einem Projekt zur Routenplanung für den Vertrieb, an dem ich gearbeitet habe, ging's darum, die Gesamtfahrstrecke so kurz wie möglich zu halten und dabei Sachen wie Fahrzeugkapazität und Lieferzeitfenster zu beachten.

Die grundlegende Struktur verstehen

Jedes lineare Programmierungsproblem hat drei Teile: Entscheidungsvariablen, eine Zielfunktion und Einschränkungen.

Entscheidungsvariablen zeigen die Entscheidungen, die du triffst. Bei Routing-Problemen können binäre Variablen angeben, welches Fahrzeug welchen Ort anfährt. In der Produktionsplanung können Variablen die Produktionsmengen darstellen.

Die Zielfunktion sagt dir, was du optimierst. Es muss eine lineare Kombination deiner Entscheidungsvariablen sein. Einschränkungen legen die Regeln und Grenzen deines Problems fest. Es gibt drei Arten: Gleichungen, Ungleichungen kleiner oder gleich und Ungleichungen größer oder gleich.

from scipy.optimize import linprog

c = [10, 15]
A_ub = [[1, 0], [0, 1]]
b_ub = [100, 80]
A_eq = [[1, 1]]
b_eq = [150]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, 
                 bounds=bounds, method='highs')

print(f"Optimal solution: Truck 1 = {result.x[0]:.1f}, Truck 2 = {result.x[1]:.1f}")
print(f"Total cost: ${result.fun:.2f}")

Der obige Code minimiert die Gesamtkosten für zwei Entscheidungsvariablen, wobei individuelle Grenzen und eine Gesamtabdeckungsanforderung zu beachten sind. Die Zielkoeffizienten [10, 15] zeigen die Kosten pro Einheit an, die Ungleichungsbeschränkungen legen den Bereich jeder Variablen fest und die Gleichungsbeschränkung sorgt dafür, dass alles abgedeckt ist.

Geometrische Interpretation

Das Verständnis der linearen Programmierung hat meine Sichtweise auf Optimierung total verändert. Jede Nebenbedingung definiert einen Halbraum, und wo sie sich schneiden, entsteht der zulässige Bereich. Diese Region ist immer ein konvexes Polytop, was bedeutet, dass jede Linie zwischen zwei inneren Punkteninnerhalb der Region bleibt.

Hier ist der entscheidende Punkt: Die besten Lösungen findest du immer an den Eckpunkten des möglichen Bereichs. Wenn du dich entlang einer Kante bewegst, verbessert das entweder dein Ziel oder nicht, also machst du weiter, bis du eine Ecke erreichst. Diese Eigenschaft macht lineare Programmieralgorithmen effizient.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 8, 400)
y1 = (10 - x) / 2
y2 = 12 - 2*x

plt.figure(figsize=(10, 8))
plt.plot(x, y1, 'r-', label='x + 2y ≤ 10', linewidth=2)
plt.plot(x, y2, 'b-', label='2x + y ≤ 12', linewidth=2)

y_feasible = np.minimum(y1, y2)
y_feasible = np.maximum(y_feasible, 0)
plt.fill_between(x, 0, y_feasible, where=(y_feasible >= 0), 
                 alpha=0.3, color='green', label='Feasible region')

vertices = [(0, 0), (0, 5), (14/3, 8/3), (6, 0)]
for v in vertices:
    plt.plot(v[0], v[1], 'ko', markersize=10)
    obj_value = 3*v[0] + 4*v[1]
    plt.annotate(f'({v[0]:.1f}, {v[1]:.1f})\nObj: {obj_value:.1f}',
                 xy=v, xytext=(v[0]+0.3, v[1]+0.3))

plt.xlim(-0.5, 8)
plt.ylim(-0.5, 8)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True, alpha=0.3)
plt.title('Geometric View: Optimal Solution at Vertex (4.7, 2.7)')
plt.show()

Diese Visualisierung zeigt die beste Lösung am Scheitelpunkt (4,7, 2,7), wo sich zwei Einschränkungen treffen. Der konvexe machbare Bereich sorgt dafür, dass es keine versteckten Täler gibt, in denen Algorithmen hängen bleiben könnten, und stellt sicher, dass lokale Optima den globalen Optima entsprechen.

Reale Probleme umsetzen

Das Schwierigste ist nicht, die Matheaufgaben zu lösen, sondern komplizierte Probleme in klare Formulierungen zu übersetzen. Das Festlegen von Variablen und Einschränkungen dauert oft länger als die eigentliche Optimierung.

Entscheidungsvariablen zu definieren, heißt, die grundlegenden Entscheidungen zu erkennen. Für die Routenplanung kannst du binäre Variablen für die Zuweisung von Fahrzeugstandorten verwenden oder kontinuierliche Variablen für die Reihenfolge der Besuche hinzufügen, um die Einschränkungen zu vereinfachen.

Beschränkungen zu erstellen heißt, Geschäftsregeln in Ungleichungen umzuwandeln. Das zeigt versteckte Annahmen. Wenn ein Manager sagt: „Jeder Standort braucht eine Lieferung“, heißt das dann genau eine oder mindestens eine? Diese Details ändern die Formulierung komplett.

Hier ist ein Beispiel für eine Formulierung mit PuLP:

from pulp import *

prob = LpProblem("Food_Bank_Routing", LpMinimize)

trucks = ['Truck_A', 'Truck_B', 'Truck_C']
centers = ['North', 'South', 'East', 'West', 'Central']

x = LpVariable.dicts("route", 
                     [(i, j) for i in trucks for j in centers],
                     cat='Binary')

distances = {
    ('Truck_A', 'North'): 15, ('Truck_A', 'South'): 20,
    ('Truck_A', 'East'): 10, ('Truck_A', 'West'): 25,
    ('Truck_A', 'Central'): 5,
    ('Truck_B', 'North'): 18, ('Truck_B', 'South'): 15,
    ('Truck_B', 'East'): 12, ('Truck_B', 'West'): 22,
    ('Truck_B', 'Central'): 8,
    ('Truck_C', 'North'): 20, ('Truck_C', 'South'): 25,
    ('Truck_C', 'East'): 15, ('Truck_C', 'West'): 18,
    ('Truck_C', 'Central'): 10,
}

prob += lpSum([distances[i, j] * x[i, j] 
               for i in trucks for j in centers])

for j in centers:
    prob += lpSum([x[i, j] for i in trucks]) == 1

max_stops = {'Truck_A': 3, 'Truck_B': 2, 'Truck_C': 3}
for i in trucks:
    prob += lpSum([x[i, j] for j in centers]) <= max_stops[i]

prob.solve()

print(f"Status: {LpStatus[prob.status]}")
print(f"Total distance: {value(prob.objective)} miles")
for i in trucks:
    route = [j for j in centers if value(x[i, j]) == 1]
    print(f"{i} visits: {', '.join(route)}")

Die obige Formulierung nutzt binäre Variablen für die Zuweisung von LKWs zu Zentren, minimiert die Gesamtentfernung, stellt sicher, dass jedes Zentrum genau eine Lieferung bekommt, und berücksichtigt die Kapazitätsgrenzen der LKWs.

Klassische Problemmuster bieten Vorlagen. Das Diätproblem minimiert die Kosten und erfüllt gleichzeitig die Ernährungsanforderungen. Transportprobleme halten die Versandkosten niedrig. Das hat direkt auf mein eigenes Routing-Problem gepasst. Wenn du diese Muster erkennst, geht das Formulieren schneller, weil du selten wirklich neue Probleme löst.

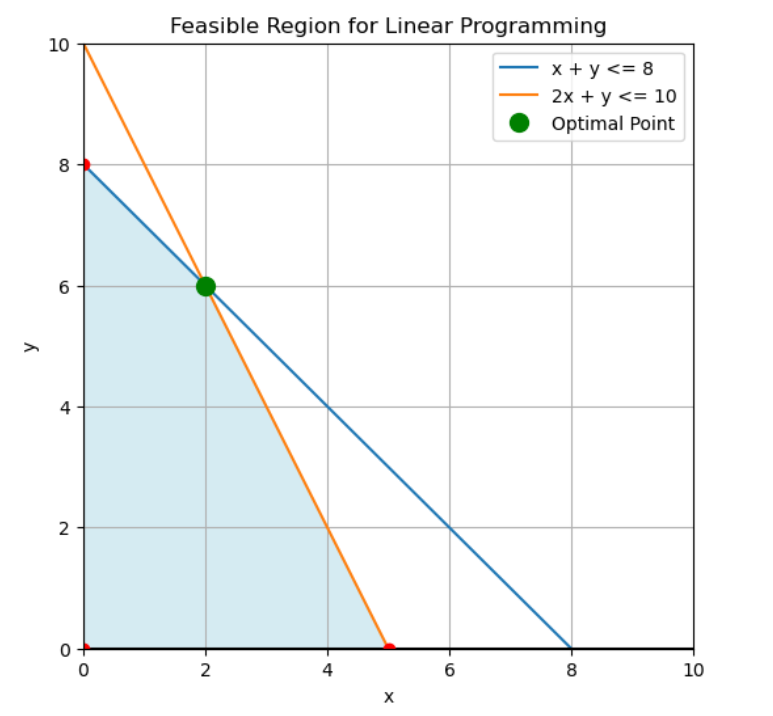
Lineare Programmierung findet die besten Lösungen an den Ecken der möglichen Bereiche, die durch Einschränkungen festgelegt sind. Bild vom Autor

Lösungsmethoden und algorithmische Ansätze

Als ich kapiert habe, wie Algorithmen funktionieren, hat sich meine Meinung über „ linprog() “ total geändert. Das sind keine Black Boxes, sondern coole mathematische Verfahren.

Simplex-Algorithmus

Der Simplex-Algorithmus, den George Dantzig 1947 entwickelt hat, ist der Ausgangspunkt. Die Idee dahinter: Man geht systematisch von einem Eckpunkt zum nächsten und verbessert dabei immer das Ziel, bis man das Optimum erreicht hat .

Der Algorithmus behält ein Tableau bei und macht Pivot-Operationen, um zwischen den Eckpunkten hin und her zu springen. Bei jeder Iteration wird das Ziel verbessert oder die Optimalität bestimmt, indem ein Pivot-Element ausgewählt und durch Zeilenoperationen aktualisiert wird.

from scipy.optimize import linprog
import numpy as np

c = [-3, -2]
A_ub = [[2, 1], [2, 3], [3, 1]]
b_ub = [18, 42, 24]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

print(f"Optimal solution: x1 = {result.x[0]:.2f}, x2 = {result.x[1]:.2f}")
print(f"Maximum value: {-result.fun:.2f}")
print(f"Iterations: {result.nit}")

Der Code oben zeigt, wie man ein Maximierungsproblem mit der Simplex-Methode löst, indem man die Zielkoeffizienten umkehrt. Der Solver springt systematisch zwischen den Eckpunkten des durch die Einschränkungen definierten Bereichs hin und her und findet die beste Lösung in nur wenigen Schritten. Bei größeren Problemen kann die Simplex-Methode das Optimum in viel weniger Schritten finden als die Anzahl der möglichen Eckpunkte, oft sogar mit weniger als 20 Iterationen, selbst wenn es Tausende von Möglichkeiten gibt.

Innenpunktmethoden

Während Simplex Grenzen überschreitet, navigieren Innenpunktmethoden durch den Innenbereich des machbaren Bereichs. Bei großen Portfolio-Optimierungsproblemen mit Hunderten von Vermögenswerten kann Simplex ziemlich langsam werden, während Innenpunktmethoden das Problem in Sekundenschnelle lösen.

Der Hauptvorteil ist die Komplexität in Polynomialzeit. Der Algorithmus von Karmarkar (1984) hat Innenpunktmethoden praktisch gemacht, indem er die Verbesserung des Ziels mit der Vermeidung von Einschränkungen in Einklang gebracht hat. Moderne Solver wie Gurobi entscheiden automatisch zwischen Simplex- und Innenpunktverfahren, je nachdem, wie das Problem aussieht.

Grafische Methode für zwei Variablen

Bei Problemen mit zwei Variablen versuche ich immer erst mal, sie grafisch zu lösen. Das hilft dabei, ein Gefühl für höhere Dimensionen zu entwickeln. Zeig die Einschränkungen auf, finde den Bereich, wo es machbar ist, und schau, welche Ecke das Ziel am besten erfüllt.

from scipy.optimize import linprog

c = [-30, -40]
A_ub = [[2, 1], [1, 2]]
b_ub = [100, 80]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

print(f"Bread loaves: {result.x[0]:.0f}")
print(f"Cakes: {result.x[1]:.0f}")
print(f"Maximum profit: ${-result.fun:.0f}")

Dieses Problem in der Bäckerei dreht sich darum, den Gewinn aus Brot und Kuchen zu maximieren, wobei die Zeit für Backen und Dekorieren begrenzt ist. Die Lösung zeigt, welcher Eckpunkt geometrisch am besten passt, und macht so das Verhalten des Algorithmus beim Vertex-Hopping klar.

Anwendungen in verschiedenen Branchen

Lineare Programmierung nutzt denselben mathematischen Ansatz, um Probleme in ganz unterschiedlichen Bereichen zu lösen.

Fertigung und Produktion

Die Produktionsplanung war meine erste richtige Anwendung. Das Produktionsmix-Problem entscheidet, wie viel produziert wird, wobei Variablen die Produktion darstellen, Ziele den Gewinn maximieren und Einschränkungen die Ressourcenbeschränkungen erfassen.

from pulp import *

products = ['Phone', 'Tablet', 'Laptop']

profits = {'Phone': 120, 'Tablet': 200, 'Laptop': 350}
assembly_time = {'Phone': 2, 'Tablet': 3, 'Laptop': 5}
testing_time = {'Phone': 1, 'Tablet': 1.5, 'Laptop': 2}

assembly_available = 500
testing_available = 200
min_production = {'Phone': 50, 'Tablet': 30, 'Laptop': 20}

model = LpProblem("Production_Planning", LpMaximize)
production = LpVariable.dicts("produce", products, lowBound=0, cat='Integer')

model += lpSum([profits[p] * production[p] for p in products])
model += lpSum([assembly_time[p] * production[p] for p in products]) <= assembly_available
model += lpSum([testing_time[p] * production[p] for p in products]) <= testing_available

for p in products:
    model += production[p] >= min_production[p]

model.solve()

print(f"Status: {LpStatus[model.status]}")
for p in products:
    print(f"{p}: {production[p].varValue:.0f} units")
print(f"Total profit: ${value(model.objective):,.0f}")

Das oben genannte Modell macht die Elektronikproduktion über drei Produktlinien hinweg besser, indem es die Montage- und Testkapazitäten mit den Mindestanforderungen für die Produktion in Einklang bringt.

Beim Mischen geht's darum, Mischungen zu optimieren, die den Anforderungen entsprechen, und das zu möglichst geringen Kosten. Ein Beispiel: Lebensmittel so mischen, dass sie den Nährwertanforderungen entsprechen und gleichzeitig die Kosten niedrig bleiben.

Transport und Logistik

Das Transportproblem ist ein weiteres Beispiel, das untersucht wurde. Die klassische Struktur hat Quellen mit Angeboten und Ziele mit Nachfragen, was die Gesamtkosten für den Transport runterbringt.

warehouses = ['Warehouse_A', 'Warehouse_B', 'Warehouse_C']
supply = {'Warehouse_A': 300, 'Warehouse_B': 400, 'Warehouse_C': 200}

customers = ['Customer_1', 'Customer_2', 'Customer_3', 'Customer_4']
demand = {'Customer_1': 200, 'Customer_2': 150, 'Customer_3': 250, 'Customer_4': 200}

costs = {
    ('Warehouse_A', 'Customer_1'): 8,  ('Warehouse_A', 'Customer_2'): 6,
    ('Warehouse_A', 'Customer_3'): 10, ('Warehouse_A', 'Customer_4'): 7,
    ('Warehouse_B', 'Customer_1'): 9,  ('Warehouse_B', 'Customer_2'): 12,
    ('Warehouse_B', 'Customer_3'): 8,  ('Warehouse_B', 'Customer_4'): 11,
    ('Warehouse_C', 'Customer_1'): 14, ('Warehouse_C', 'Customer_2'): 7,
    ('Warehouse_C', 'Customer_3'): 10, ('Warehouse_C', 'Customer_4'): 12,
}

model = LpProblem("Transportation", LpMinimize)

routes = [(w, c) for w in warehouses for c in customers]
shipments = LpVariable.dicts("ship", routes, lowBound=0)

model += lpSum([costs[i, j] * shipments[i, j] for (i, j) in routes])

for w in warehouses:
    model += lpSum([shipments[w, c] for c in customers]) <= supply[w]

for c in customers:
    model += lpSum([shipments[w, c] for w in warehouses]) >= demand[c]

model.solve()

Netzwerkflussprobleme machen den Transport zu Graphen mit Umschlagknoten. Ich hab gelesen, dass Fluggesellschaften das oft für die Planung der Crews und die Routen der Flugzeuge nutzen.

Finanzdienstleistungen und Gesundheitswesen

Bei Finanzanwendungen wählt die Kapitalbudgetierung Projekte aus, die die Rendite unter Berücksichtigung der Budgetbeschränkungen maximieren:

projects = {
    'Project_A': {'return': 25000, 'cost': 100000, 'staff': 5},
    'Project_B': {'return': 30000, 'cost': 150000, 'staff': 7},
    'Project_C': {'return': 20000, 'cost': 80000, 'staff': 4},
}

budget = 300000
staff_available = 15

model = LpProblem("Capital_Budgeting", LpMaximize)
select = LpVariable.dicts("select", projects.keys(), cat='Binary')

model += lpSum([projects[p]['return'] * select[p] for p in projects])
model += lpSum([projects[p]['cost'] * select[p] for p in projects]) <= budget
model += lpSum([projects[p]['staff'] * select[p] for p in projects]) <= staff_available

model.solve()

Gesundheitssysteme stehen vor endlosen Optimierungsherausforderungen. Ich hab bei einem Problem mit der Dienstplanung in einer Klinik geholfen, bei dem Krankenschwestern ihren Schichten zugeteilt wurden, wobei die Anforderungen an die Qualifikation und die Auslastung berücksichtigt wurden.

Moderne Technologieanwendungen

Lineare Programmierung taucht auch überraschend im Bereich des maschinellen Lernens auf. Die Merkmalsauswahl kann so formuliert werden, dass der Vorhersagefehler unter Berücksichtigung von Sparsamkeitsbeschränkungen minimiert wird. Cloud Computing nutzt es für die Ressourcenzuteilung über verteilte Systeme hinweg.

Rechenaufwand und Leistung

Komplexität ist wichtig, wenn Probleme von einfachen Beispielen zu Produktionssystemen werden.

Komplexität des Simplex-Algorithmus

Simplex hat eine echt spannende Komplexität. Es hat im schlimmsten Fall eine exponentielle Leistung, aber im Durchschnitt ist es echt gut. Bei komischen Fällen wie dem Klee-Minty-Würfel muss man jeden Eckpunkt anschauen, aber bei normalen Problemen checkt man nur einen kleinen Teil, der ungefähr quadratisch skaliert.

Ich habe das getestet, indem ich zufällig generierte Probleme mit zunehmendem Umfang gelöst habe:

import time
import numpy as np
from scipy.optimize import linprog

def benchmark_simplex(num_vars, num_constraints):
    c = np.random.randn(num_vars)
    A_ub = np.random.randn(num_constraints, num_vars)
    b_ub = np.random.rand(num_constraints) * 10
    
    start = time.time()
    result = linprog(c, A_ub=A_ub, b_ub=b_ub, method='simplex')
    elapsed = time.time() - start
    
    return elapsed, result.nit

problem_sizes = [(10, 20), (50, 100), (100, 200), (200, 400)]

for n_vars, n_const in problem_sizes:
    times, iterations = [], []
    for _ in range(10):
        t, it = benchmark_simplex(n_vars, n_const)
        times.append(t)
        iterations.append(it)
    print(f"{n_vars}x{n_const}: {np.mean(times):.4f}s, {np.mean(iterations):.1f} iterations")

Meine Benchmarks haben gezeigt, dass eine Verdopplung der Problemgröße die Zeit um weniger als das Vierfache verlängert hat, was ein nahezu polynomiales Verhalten für typische Verteilungen bestätigt.

Leistungsverbesserungen

Moderne Solver machen durch Vorverarbeitung, Parallelverarbeitung und automatische Algorithmusauswahl echt gute Arbeit. Durch Vorverarbeitung kann die Problemgröße vor der Lösung automatisch um 30 % oder mehr reduziert werden.

Degeneration passiert, wenn mehrere Einschränkungen am Optimum eng sind, was zu Zyklen führen kann. Ich bin darauf gestoßen, als zwei Routen die gleichen Kosten hatten. Löser nutzen Störungstechniken, um Zyklen zu vermeiden, auch wenn degenerierte Probleme langsamer gelöst werden.

Bei schlecht skalierten Problemen kommt es zu numerischer Instabilität. Das Mischen von Geldbeträgen (Tausende von Dollar) mit Mengen (Einzelstücke) hat zu Warnungen des Solvers geführt. Durch die Neuskalierung war das Problem sofort behoben.

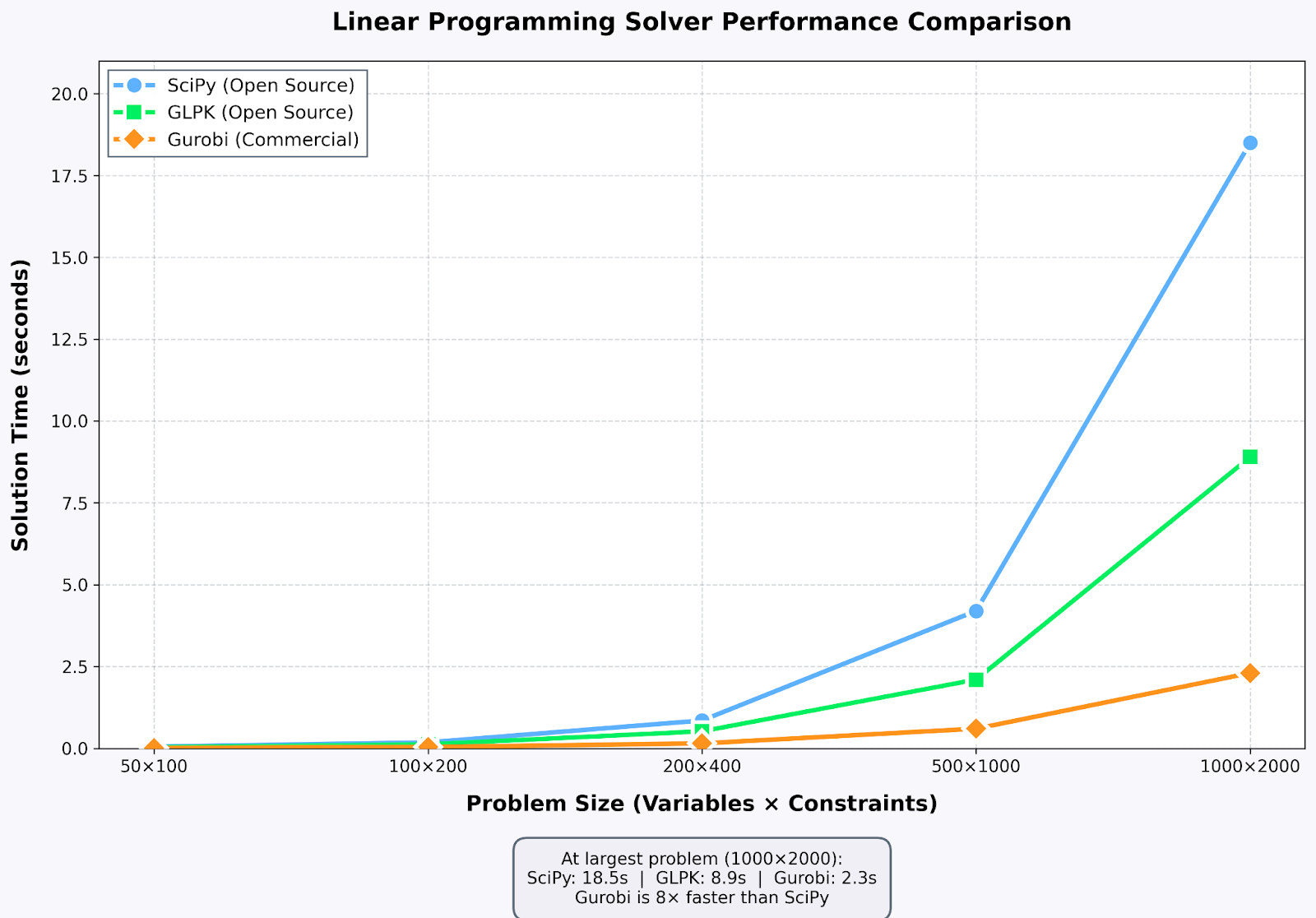
Vergleich der Solver-Leistung: Kommerzielle Lösungen sind bei großen Problemen echt gut. Bild vom Autor

Softwaretools und Implementierung

Die Wahl der Werkzeuge beeinflusst die Produktivität stark. Ich hab mich von der manuellen Programmierung einfacher Programme zu professionellen Lösungsprogrammen für viel größere Probleme weiterentwickelt.

Kommerzielle Solver und Modellierungssprachen

CPLEX und Gurobi sind die Top-Anbieter für industrielle Optimierung und bieten bei großen Problemen eine um ein Vielfaches bessere Leistung als Open-Source-Alternativen. Ich hab die akademische Lizenz von Gurobi für die Arbeit an der Lieferkette genutzt. Probleme, die mit SciPy Minuten dauern, sind in Sekundenschnelle gelöst.

PuLP ist mein Lieblingsprogramm in Python. Es bietet eine übersichtliche API zum Erstellen von Modellen, die von verschiedenen Backends gelöst werden:

from pulp import *

model = LpProblem("my_problem", LpMaximize)

x = LpVariable("x", lowBound=0)
y = LpVariable("y", lowBound=0)

model += 3*x + 2*y
model += x + y <= 100
model += 2*x + y <= 150

model.solve()

print(f"Used solver: {model.solver}")
print(f"Status: {LpStatus[model.status]}")

Die Abstraktionsschicht ist Code, der unabhängig vom Solver auf verschiedenen Systemen läuft. Pyomo hat noch mehr coole Funktionen für komplizierte Optimierungen, wie nichtlineare und stochastische Programmierung.

Cloud- und Open-Source-Alternativen

Cloud-Plattformen bieten Optimierung als Dienstleistung für unregelmäßige, groß angelegte Probleme. Du lädst Problemdaten hoch und bekommst Lösungen über die API. Die serverlose Architektur ist echt elegant, aber bei kleinen Problemen langsamer als lokale Solver.

GLPK (GNU Linear Programming Kit) ist das zuverlässige Open-Source-Arbeitstier. Ich benutze es für den Unterricht und für persönliche Projekte. HiGHS ist ein neuerer Solver, der echt gut funktioniert. SciPy hat vor kurzem HiGHS als Standard-Backend übernommen, und meine Benchmarks haben gezeigt, dass es bei vielen Problemen mit Gurobi mithalten kann.

Beispiele für lineare Programmierung

Das Durcharbeiten kompletter Beispiele hilft besser beim Verstehen als nur die Theorie.

Beispiel 1: Ernährungsproblem

Das klassische Diätproblem minimiert die Kosten und erfüllt gleichzeitig die Ernährungsanforderungen:

from pulp import *

foods = {
    'Oatmeal': {'cost': 0.50, 'calories': 110, 'protein': 4, 'vitamin': 2},
    'Chicken': {'cost': 2.50, 'calories': 250, 'protein': 30, 'vitamin': 0},
    'Eggs':    {'cost': 0.80, 'calories': 155, 'protein': 13, 'vitamin': 1},
    'Milk':    {'cost': 1.20, 'calories': 150, 'protein': 8, 'vitamin': 4},
    'Bread':   {'cost': 0.30, 'calories': 80, 'protein': 3, 'vitamin': 0}
}

min_calories, min_protein, min_vitamin = 2000, 50, 10

model = LpProblem("Diet_Optimization", LpMinimize)
servings = LpVariable.dicts("servings", foods.keys(), lowBound=0)

model += lpSum([foods[f]['cost'] * servings[f] for f in foods])
model += lpSum([foods[f]['calories'] * servings[f] for f in foods]) >= min_calories
model += lpSum([foods[f]['protein'] * servings[f] for f in foods]) >= min_protein
model += lpSum([foods[f]['vitamin'] * servings[f] for f in foods]) >= min_vitamin

model.solve()

print(f"Total cost: ${value(model.objective):.2f}")
for food in foods:
    if servings[food].varValue > 0.01:
        print(f"{food}: {servings[food].varValue:.2f} servings")

Die obige Formel findet die günstigste Kombination von Lebensmitteln, die den täglichen Nährstoffbedarf deckt. Das zeigt, dass optimale LP-Lösungen ohne zusätzliche Einschränkungen hinsichtlich Vielfalt, Geschmack oder Ernährungsgewohnheiten nicht immer praktikabel sind.

Das gleiche Rahmenwerk kann auch als Grundlage für geschäftliche Entscheidungen dienen, wie zum Beispiel die Optimierung von Produktionsplänen oder die Zuweisung von Marketingbudgets.

Beispiel 2: Mehrperiodenplanung

Bei der Mehrperiodenplanung wird geschaut, wie sich die Lagerbestände auf den zukünftigen Bedarf über mehrere Zeiträume auswirken:

days = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']

centers = {
    'North': {'daily_demand': [100, 80, 90, 110, 85], 'capacity': 250},
    'South': {'daily_demand': [120, 100, 95, 105, 130], 'capacity': 300},
}

delivery_cost = {'Monday': 50, 'Tuesday': 50, 'Wednesday': 50,
                 'Thursday': 50, 'Friday': 70}

model = LpProblem("Multiperiod_Routing", LpMinimize)

deliveries = LpVariable.dicts("deliver",
                              [(c, d) for c in centers for d in days],
                              lowBound=0)
inventory = LpVariable.dicts("inventory",
                            [(c, d) for c in centers for d in days],
                            lowBound=0)

model += lpSum([delivery_cost[d] * deliveries[c, d] 
                for c in centers for d in days])

for c in centers:
    for i, day in enumerate(days):
        if i == 0:
            model += inventory[c, day] == deliveries[c, day] - centers[c]['daily_demand'][i]
        else:
            prev_day = days[i-1]
            model += (inventory[c, day] == inventory[c, prev_day] + 
                     deliveries[c, day] - centers[c]['daily_demand'][i])
        model += inventory[c, day] <= centers[c]['capacity']

model.solve()

Mehrperiodenmodelle machen Probleme größer, ermöglichen aber auch eine ausgeklügelte Optimierung. Das Modell fasst Lieferungen an günstigeren Tagen zusammen und nutzt Lagerkapazitäten, um die Gesamtkosten zu senken.

Gemischte ganzzahlige Programmierung

Viele Probleme haben mit einzelnen Entscheidungen zu tun: eine Anlage bauen oder nicht, einen Mitarbeiter einteilen oder nicht. Dafür braucht man gemischt-ganzzahlige Programmierung (MIP), die lineare Programmierung mit ganzzahligen und binären Variablen erweitert.

Einführung und Branch-and-Bound

Routing-Probleme brauchen ganzzahlige Entscheidungen. Die binäre Variable „ x[i][j] ” zeigt an, ob Fahrzeug i den Standort j besucht. Fahrzeuge können keine Teilbesuche machen.

Branch-and-Bound durchsucht systematisch einen diskreten Lösungsraum, indem es kontinuierliche LP-Relaxationen löst:

from pulp import *

model_continuous = LpProblem("Continuous", LpMaximize)
x_cont = LpVariable("x", lowBound=0)
y_cont = LpVariable("y", lowBound=0)

model_continuous += 3*x_cont + 4*y_cont
model_continuous += x_cont + 2*y_cont <= 10
model_continuous += 2*x_cont + y_cont <= 12

model_continuous.solve()
print(f"Continuous: x={x_cont.varValue:.2f}, y={y_cont.varValue:.2f}")

model_integer = LpProblem("Integer", LpMaximize)
x_int = LpVariable("x", lowBound=0, cat='Integer')
y_int = LpVariable("y", lowBound=0, cat='Integer')

model_integer += 3*x_int + 4*y_int
model_integer += x_int + 2*y_int <= 10
model_integer += 2*x_int + y_int <= 12

model_integer.solve()
print(f"Integer: x={x_int.varValue:.0f}, y={y_int.varValue:.0f}")

Die ganzzahlige Lösung ist anders als die Rundung der kontinuierlichen Lösung. Branch-and-Bound findet die beste ganzzahlige Lösung, aber das kostet viel mehr Rechenzeit.

Wann man ganzzahlige Programmierung einsetzt

Verwende ganzzahlige Variablen, wenn Entscheidungen von Natur aus diskret sind: Öffnen von Einrichtungen, Zuweisen von Mitarbeitern, Routenplanung für Fahrzeuge. Optimierungen auf dem Anleihemarkt brauchen oft gemischte ganzzahlige Lösungen. Kontinuierliche Variablen können manchmal seltsame Bruchteilzuweisungen ergeben, während binäre Variablen umsetzbare Lösungen liefern.

Allerdings ist die ganzzahlige Programmierung deutlich teurer. Probleme mit Hunderten von ganzzahligen Variablen können Stunden dauern, während kontinuierliche LPs nur Sekunden brauchen. Bei großen Produktionsmengen ist die Integrität weniger wichtig, da das Runden die Lösungen kaum beeinflusst. Löse immer zuerst die kontinuierliche Relaxation, um die Grenzen zu überprüfen, bevor du dich auf die vollständige ganzzahlige Programmierung festlegst.

Fazit

Lineare Programmierung verändert die Art und Weise, wie du Optimierungsprobleme angehst. Das gleiche mathematische Konzept wird in ganz unterschiedlichen Bereichen angewendet, von der Routenplanung über die Produktionsplanung bis hin zum Portfoliomanagement.

Fang mit einfachen Problemen mit zwei Variablen an, die du dir geometrisch vorstellen kannst. Setze ein einfaches Simplex-Verfahren ein, um zu verstehen, was kommerzielle Solver im Hintergrund machen. Arbeite mit echten Formulierungen und setz geschäftliche Anforderungen in mathematische Bedingungen um.

Um dein Fachwissen zu vertiefen, schau dir unsere Kurse „Einführung in die Optimierung in Python“ und „Lineare Algebra für Data Science“ an, um deine mathematischen Grundlagen zu stärken. Unser Lernpfad als Machine Learning Scientist in Python ist auch eine super Option.