Programação Linear: Resolvendo problemas de otimização do mundo real

Os gerentes de operações enfrentam um desafio constante: muitas decisões, muitas limitações e nenhuma maneira óbvia de encontrar a melhor solução. Uma rede de distribuição precisa minimizar os custos com combustível em várias rotas, respeitando os prazos de entrega, a capacidade dos veículos e os horários dos motoristas.

Esses dois problemas têm uma estrutura matemática parecida. Quando seus objetivos e restrições podem ser expressos como relações lineares, você está lidando com um problema de programação linear. A gente se preocupa com a programação linear porque ela encontra as melhores soluções quando você está trabalhando com recursos limitados e requisitos concorrentes.

O que torna a programação linear tão poderosa é a garantia que ela dá: se existe uma solução viável, o algoritmo vai encontrar a melhor. Claro, as aplicações do mundo real raramente se encaixam perfeitamente nos exemplos dos livros didáticos, mas entender a estrutura básica ajuda a reconhecer quando a otimização pode substituir as suposições.

Este guia te leva desde o básico até implementações funcionais em Python. Vamos avançar de problemas simples com duas variáveis, que você pode visualizar geometricamente, para cenários complexos que exigem soluções algorítmicas. Você vai entender tanto a teoria matemática que faz a otimização funcionar quanto as habilidades práticas para implementar as soluções por conta própria.

O que é Programação Linear?

A programação linear otimiza uma função objetivo linear sujeita a restrições lineares. Num projeto de roteirização de distribuição em que trabalhei, o objetivo era minimizar a distância total percorrida, respeitando restrições como a capacidade do veículo e os prazos de entrega.

Entendendo a estrutura básica

Todo problema de programação linear tem três partes: variáveis de decisão, uma função objetivo e restrições.

As variáveis de decisão são as escolhas que você faz. Em problemas de roteamento, variáveis binárias podem indicar qual veículo visita qual local. No planejamento da produção, as variáveis podem representar quantidades de fabricação.

A função objetivo define o que você está otimizando. Tem que ser uma combinação linear das suas variáveis de decisão. As restrições definem as regras e limitações do seu problema. Elas podem ser de três tipos: igualdades, desigualdades menores ou iguais e desigualdades maiores ou iguais.

from scipy.optimize import linprog

c = [10, 15]
A_ub = [[1, 0], [0, 1]]
b_ub = [100, 80]
A_eq = [[1, 1]]
b_eq = [150]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, 
                 bounds=bounds, method='highs')

print(f"Optimal solution: Truck 1 = {result.x[0]:.1f}, Truck 2 = {result.x[1]:.1f}")
print(f"Total cost: ${result.fun:.2f}")

O código acima minimiza o custo total para duas variáveis de decisão, sujeito a limites individuais e a um requisito de cobertura total. Os coeficientes objetivos [10, 15] mostram o custo por unidade, as restrições de desigualdade limitam o intervalo de cada variável e a restrição de igualdade garante a cobertura total.

Interpretação geométrica

Entender a programação linear mudou completamente a minha maneira de pensar sobre otimização. Cada restrição define um semi-espaço, e a interseção deles forma a região viável. Essa região é um poliedro sempre convexo, o que significa que qualquer linha entre dois pontos internosfica dentro dela.

Aqui está a ideia crucial: as soluções ótimas sempre ocorrem nos vértices da região viável. Mover-se ao longo de uma borda pode melhorar seu objetivo ou não, então você continua se movendo até chegar a um canto. Essa propriedade torna os algoritmos de programação linear eficientes.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 8, 400)
y1 = (10 - x) / 2
y2 = 12 - 2*x

plt.figure(figsize=(10, 8))
plt.plot(x, y1, 'r-', label='x + 2y ≤ 10', linewidth=2)
plt.plot(x, y2, 'b-', label='2x + y ≤ 12', linewidth=2)

y_feasible = np.minimum(y1, y2)
y_feasible = np.maximum(y_feasible, 0)
plt.fill_between(x, 0, y_feasible, where=(y_feasible >= 0), 
                 alpha=0.3, color='green', label='Feasible region')

vertices = [(0, 0), (0, 5), (14/3, 8/3), (6, 0)]
for v in vertices:
    plt.plot(v[0], v[1], 'ko', markersize=10)
    obj_value = 3*v[0] + 4*v[1]
    plt.annotate(f'({v[0]:.1f}, {v[1]:.1f})\nObj: {obj_value:.1f}',
                 xy=v, xytext=(v[0]+0.3, v[1]+0.3))

plt.xlim(-0.5, 8)
plt.ylim(-0.5, 8)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True, alpha=0.3)
plt.title('Geometric View: Optimal Solution at Vertex (4.7, 2.7)')
plt.show()

Essa visualização mostra a solução ideal no vértice (4,7, 2,7), onde duas restrições se cruzam. A região viável convexa garante que não haja vales ocultos onde os algoritmos possam ficar presos, garantindo que os ótimos locais sejam iguais aos ótimos globais.

Transformando problemas do mundo real

A parte mais difícil não é resolver a matemática, mas transformar problemas confusos em fórmulas claras. Definir variáveis e restrições geralmente leva mais tempo do que fazer a otimização em si.

Definir variáveis de decisão requer identificar escolhas fundamentais. Para o roteamento, você pode usar variáveis binárias para atribuições de localização de veículos ou adicionar variáveis contínuas para ordenação de visitas para simplificar as restrições.

Construir restrições significa transformar regras de negócios em desigualdades. Isso mostra suposições que a gente nem percebe. Quando um gerente diz “cada local precisa de uma entrega”, isso quer dizer exatamente uma ou pelo menos uma? Esses detalhes mudam completamente a fórmula.

Aqui está um exemplo de formulação usando PuLP:

from pulp import *

prob = LpProblem("Food_Bank_Routing", LpMinimize)

trucks = ['Truck_A', 'Truck_B', 'Truck_C']
centers = ['North', 'South', 'East', 'West', 'Central']

x = LpVariable.dicts("route", 
                     [(i, j) for i in trucks for j in centers],
                     cat='Binary')

distances = {
    ('Truck_A', 'North'): 15, ('Truck_A', 'South'): 20,
    ('Truck_A', 'East'): 10, ('Truck_A', 'West'): 25,
    ('Truck_A', 'Central'): 5,
    ('Truck_B', 'North'): 18, ('Truck_B', 'South'): 15,
    ('Truck_B', 'East'): 12, ('Truck_B', 'West'): 22,
    ('Truck_B', 'Central'): 8,
    ('Truck_C', 'North'): 20, ('Truck_C', 'South'): 25,
    ('Truck_C', 'East'): 15, ('Truck_C', 'West'): 18,
    ('Truck_C', 'Central'): 10,
}

prob += lpSum([distances[i, j] * x[i, j] 
               for i in trucks for j in centers])

for j in centers:
    prob += lpSum([x[i, j] for i in trucks]) == 1

max_stops = {'Truck_A': 3, 'Truck_B': 2, 'Truck_C': 3}
for i in trucks:
    prob += lpSum([x[i, j] for j in centers]) <= max_stops[i]

prob.solve()

print(f"Status: {LpStatus[prob.status]}")
print(f"Total distance: {value(prob.objective)} miles")
for i in trucks:
    route = [j for j in centers if value(x[i, j]) == 1]
    print(f"{i} visits: {', '.join(route)}")

A fórmula acima usa variáveis binárias para atribuições de caminhões a centros, minimiza a distância total, garante que cada centro receba exatamente uma entrega e respeita os limites de capacidade dos caminhões.

Os padrões clássicos de problemas fornecem modelos. A dieta resolve o problema de minimizar os custos e, ao mesmo tempo, atender às necessidades nutricionais. Problemas de transporte minimizam os custos de envio. Isso se aplicava diretamente ao meu próprio desafio de roteamento. Reconhecer esses padrões ajuda a acelerar a formulação, já que você raramente está resolvendo problemas realmente novos.

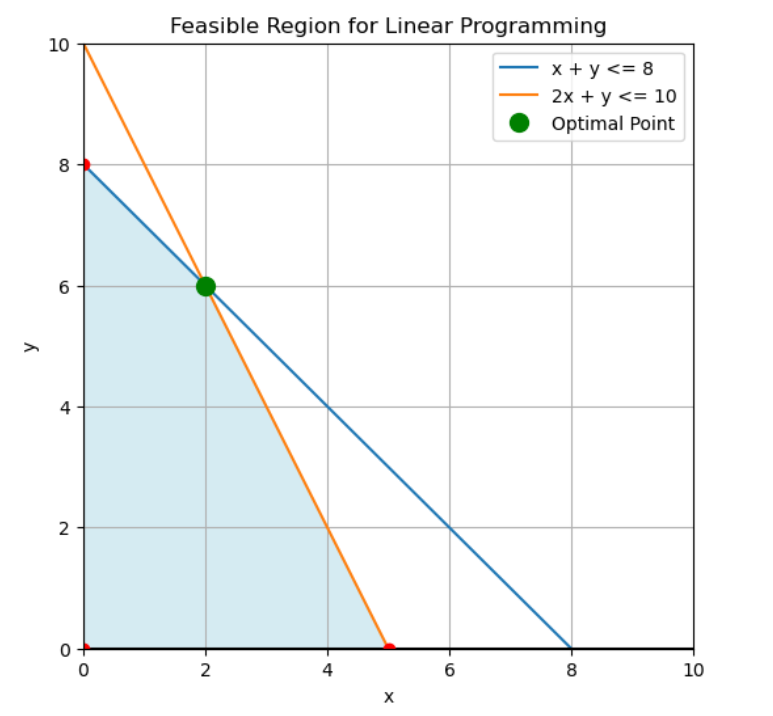
A programação linear encontra soluções ótimas nos vértices das regiões viáveis definidas por restrições. Imagem do autor

Métodos de solução e abordagens algorítmicas

Entender como os algoritmos funcionam mudou minha opinião sobre ligar para linprog(). Não são caixas pretas, mas sim procedimentos matemáticos bem legais.

Algoritmo Simplex

O algoritmo simplex, criado por George Dantzig em 1947, é o ponto de partida. Sua ideia: percorrer sistematicamente de vértice a vértice adjacente, sempre melhorando o objetivo, até chegar ao ótimo.

O algoritmo mantém um quadro e faz operações de pivô para se mover entre os vértices. Cada repetição melhora o objetivo ou determina a otimização, escolhendo um elemento pivô e atualizando através de operações de linha.

from scipy.optimize import linprog
import numpy as np

c = [-3, -2]
A_ub = [[2, 1], [2, 3], [3, 1]]
b_ub = [18, 42, 24]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

print(f"Optimal solution: x1 = {result.x[0]:.2f}, x2 = {result.x[1]:.2f}")
print(f"Maximum value: {-result.fun:.2f}")
print(f"Iterations: {result.nit}")

O código acima mostra como resolver um problema de maximização com o método simplex, invertendo os coeficientes do objetivo. O solucionador se move sistematicamente entre os vértices da região viável definida pelas restrições, chegando à solução ideal em apenas algumas iterações. Em problemas maiores, o método simplex consegue encontrar o ótimo em muito menos etapas do que o número de vértices viáveis, muitas vezes em menos de 20 iterações, mesmo com milhares de possibilidades.

Métodos de ponto interior

Enquanto o simplex atravessa limites, os métodos de ponto interior navegam pelo interior da região viável. Para problemas de otimização de grandes portfólios com centenas de ativos, o simplex pode ficar lento, enquanto os métodos de ponto interior resolvem em segundos.

A principal vantagem é a complexidade em tempo polinomial. O algoritmo de Karmarkar (1984) tornou os métodos de ponto interior práticos, equilibrando a melhoria objetiva com a manutenção de uma distância segura das fronteiras de restrição. Solucionadores modernos como o Gurobi escolhem automaticamente entre simplex e ponto interior com base nas características do problema.

Método gráfico para duas variáveis

Para problemas com duas variáveis, eu sempre resolvo primeiro graficamente. Isso desenvolve a intuição que se transfere para dimensões superiores. Traça restrições, identifica a região viável e descobre qual canto otimiza o objetivo.

from scipy.optimize import linprog

c = [-30, -40]
A_ub = [[2, 1], [1, 2]]
b_ub = [100, 80]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

print(f"Bread loaves: {result.x[0]:.0f}")
print(f"Cakes: {result.x[1]:.0f}")
print(f"Maximum profit: ${-result.fun:.0f}")

Esse problema de produção de padaria maximiza o lucro com pães e bolos, levando em conta os limites de tempo do forno e da decoração. A solução mostra qual ponto de canto é o melhor geometricamente, deixando claro como o algoritmo pula de vértice em vértice.

Aplicações em todos os setores

A programação linear usa a mesma estrutura matemática para resolver problemas em áreas bem diferentes.

Fabricação e produção

O planejamento da produção foi minha primeira aplicação séria. O problema do mix de produção determina as quantidades fabricadas, com variáveis que representam a produção, objetivos que maximizam o lucro e restrições que capturam as limitações de recursos.

from pulp import *

products = ['Phone', 'Tablet', 'Laptop']

profits = {'Phone': 120, 'Tablet': 200, 'Laptop': 350}
assembly_time = {'Phone': 2, 'Tablet': 3, 'Laptop': 5}
testing_time = {'Phone': 1, 'Tablet': 1.5, 'Laptop': 2}

assembly_available = 500
testing_available = 200
min_production = {'Phone': 50, 'Tablet': 30, 'Laptop': 20}

model = LpProblem("Production_Planning", LpMaximize)
production = LpVariable.dicts("produce", products, lowBound=0, cat='Integer')

model += lpSum([profits[p] * production[p] for p in products])
model += lpSum([assembly_time[p] * production[p] for p in products]) <= assembly_available
model += lpSum([testing_time[p] * production[p] for p in products]) <= testing_available

for p in products:
    model += production[p] >= min_production[p]

model.solve()

print(f"Status: {LpStatus[model.status]}")
for p in products:
    print(f"{p}: {production[p].varValue:.0f} units")
print(f"Total profit: ${value(model.objective):,.0f}")

O modelo acima otimiza a produção de eletrônicos em três linhas de produtos, equilibrando a capacidade de montagem e teste com os requisitos mínimos de produção.

Os problemas de mistura otimizam as misturas que atendem às especificações com o menor custo possível, como misturar alimentos para atender às necessidades nutricionais e, ao mesmo tempo, minimizar os custos.

Transporte e logística

O problema do transporte é outro exemplo que a gente estuda. A estrutura clássica tem fontes com suprimentos e destinos com demandas, minimizando o custo total de envio.

warehouses = ['Warehouse_A', 'Warehouse_B', 'Warehouse_C']
supply = {'Warehouse_A': 300, 'Warehouse_B': 400, 'Warehouse_C': 200}

customers = ['Customer_1', 'Customer_2', 'Customer_3', 'Customer_4']
demand = {'Customer_1': 200, 'Customer_2': 150, 'Customer_3': 250, 'Customer_4': 200}

costs = {
    ('Warehouse_A', 'Customer_1'): 8,  ('Warehouse_A', 'Customer_2'): 6,
    ('Warehouse_A', 'Customer_3'): 10, ('Warehouse_A', 'Customer_4'): 7,
    ('Warehouse_B', 'Customer_1'): 9,  ('Warehouse_B', 'Customer_2'): 12,
    ('Warehouse_B', 'Customer_3'): 8,  ('Warehouse_B', 'Customer_4'): 11,
    ('Warehouse_C', 'Customer_1'): 14, ('Warehouse_C', 'Customer_2'): 7,
    ('Warehouse_C', 'Customer_3'): 10, ('Warehouse_C', 'Customer_4'): 12,
}

model = LpProblem("Transportation", LpMinimize)

routes = [(w, c) for w in warehouses for c in customers]
shipments = LpVariable.dicts("ship", routes, lowBound=0)

model += lpSum([costs[i, j] * shipments[i, j] for (i, j) in routes])

for w in warehouses:
    model += lpSum([shipments[w, c] for c in customers]) <= supply[w]

for c in customers:
    model += lpSum([shipments[w, c] for w in warehouses]) >= demand[c]

model.solve()

Os problemas de fluxo de rede generalizam o transporte para gráficos com nós de transbordo. Li que as companhias aéreas utilizam bastante isso para a programação das tripulações e o roteamento das aeronaves.

Serviços financeiros e saúde

Em aplicações financeiras, o orçamento de capital escolhe projetos que maximizam o retorno, levando em conta as restrições orçamentárias:

projects = {
    'Project_A': {'return': 25000, 'cost': 100000, 'staff': 5},
    'Project_B': {'return': 30000, 'cost': 150000, 'staff': 7},
    'Project_C': {'return': 20000, 'cost': 80000, 'staff': 4},
}

budget = 300000
staff_available = 15

model = LpProblem("Capital_Budgeting", LpMaximize)
select = LpVariable.dicts("select", projects.keys(), cat='Binary')

model += lpSum([projects[p]['return'] * select[p] for p in projects])
model += lpSum([projects[p]['cost'] * select[p] for p in projects]) <= budget
model += lpSum([projects[p]['staff'] * select[p] for p in projects]) <= staff_available

model.solve()

Os sistemas de saúde enfrentam desafios intermináveis de otimização. Eu dei uma força num problema de agendamento de uma clínica que precisava distribuir os turnos das enfermeiras, respeitando os requisitos de qualificação e o equilíbrio da carga de trabalho.

Aplicações da tecnologia moderna

A programação linear também aparece de surpresa na área de machine learning. A seleção de características pode ser formulada como a minimização do erro de previsão sujeita a restrições de dispersão. A nuvem usa isso pra alocar recursos em sistemas distribuídos.

Complexidade computacional e desempenho

A complexidade é importante quando os problemas passam de exemplos simples para sistemas de produção.

Complexidade do algoritmo Simplex

Simplex tem um nível de complexidade fascinante. Tem um desempenho exponencial no pior dos casos, mas excelente no caso médio. Casos patológicos como o cubo de Klee-Minty obrigam a examinar todos os vértices, mas os problemas típicos examinam apenas uma pequena fração, escalando aproximadamente de forma quadrática.

Testei isso resolvendo problemas gerados aleatoriamente e de tamanho crescente:

import time
import numpy as np
from scipy.optimize import linprog

def benchmark_simplex(num_vars, num_constraints):
    c = np.random.randn(num_vars)
    A_ub = np.random.randn(num_constraints, num_vars)
    b_ub = np.random.rand(num_constraints) * 10
    
    start = time.time()
    result = linprog(c, A_ub=A_ub, b_ub=b_ub, method='simplex')
    elapsed = time.time() - start
    
    return elapsed, result.nit

problem_sizes = [(10, 20), (50, 100), (100, 200), (200, 400)]

for n_vars, n_const in problem_sizes:
    times, iterations = [], []
    for _ in range(10):
        t, it = benchmark_simplex(n_vars, n_const)
        times.append(t)
        iterations.append(it)
    print(f"{n_vars}x{n_const}: {np.mean(times):.4f}s, {np.mean(iterations):.1f} iterations")

Meus benchmarks mostraram que dobrar o tamanho do problema aumentou o tempo em menos de 4 vezes, confirmando um comportamento quase polinomial para distribuições típicas.

Melhorias no desempenho

Os solucionadores modernos têm um desempenho incrível por causa do pré-processamento, processamento paralelo e seleção automática de algoritmos. O pré-processamento pode reduzir o tamanho do problema em 30% ou mais automaticamente antes da resolução.

A degeneração rola quando várias restrições ficam apertadas no ponto ideal, o que pode causar ciclagem. Eu me deparei com isso quando duas rotas tinham custos iguais. Os solucionadores usam técnicas de perturbação para evitar ciclos, embora os problemas degenerados sejam resolvidos mais lentamente.

A instabilidade numérica surge com problemas mal dimensionados. Misturar valores monetários (milhares de dólares) com quantidades (unidades individuais) causou avisos do solucionador. Redimensionar resolveu o problema na hora.

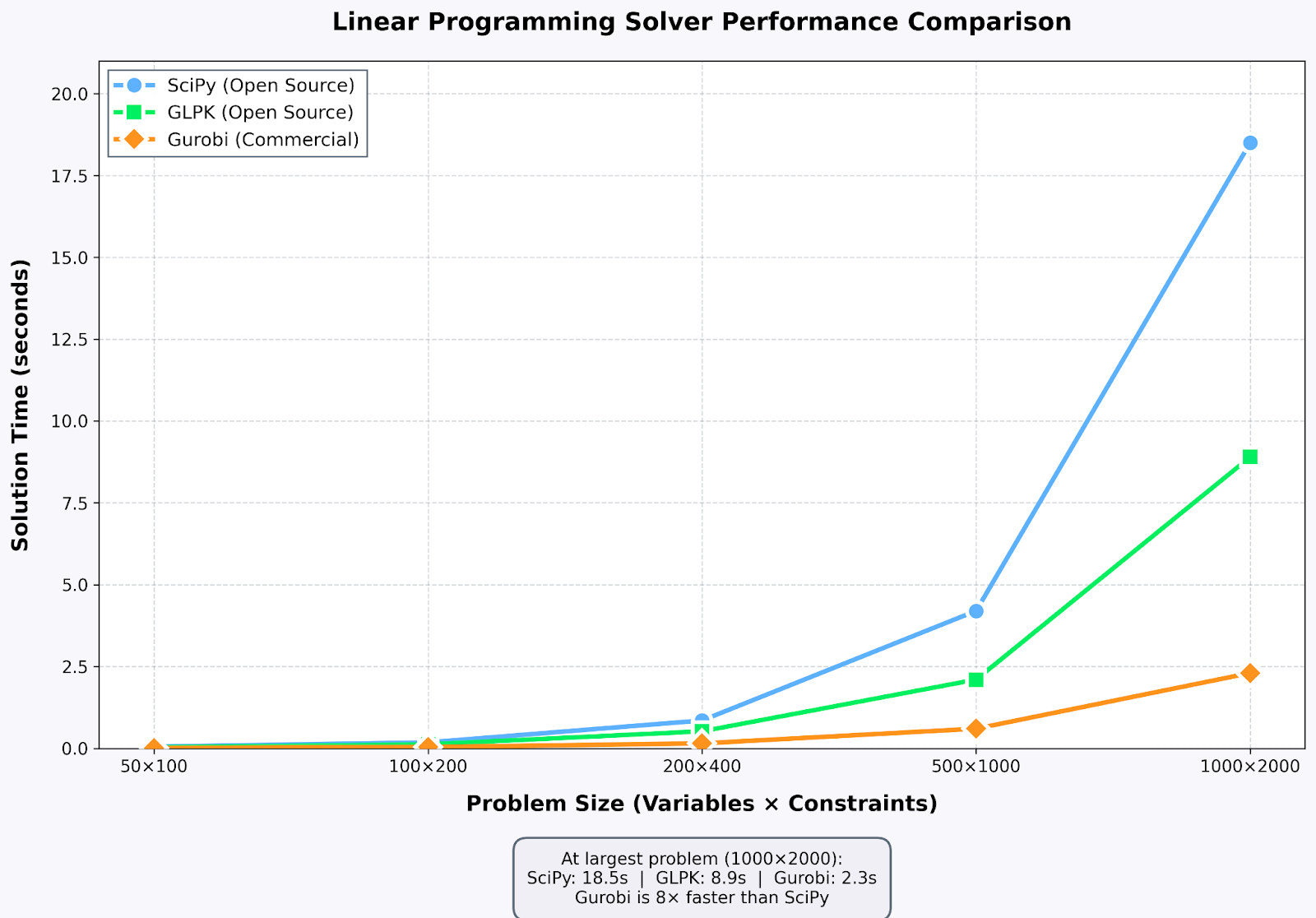
Comparando o desempenho dos solucionadores: as soluções comerciais são ótimas pra resolver problemas grandes. Imagem do autor

Ferramentas de software e implementação

A escolha da ferramenta afeta muito a produtividade. Eu evoluí da codificação manual simplex para o uso de solucionadores profissionais que lidam com problemas muito maiores.

Solucionadores comerciais e linguagens de modelagem

O CPLEX e o Gurobi são os líderes em otimização industrial, oferecendo um desempenho muito melhor do que as alternativas de código aberto para problemas grandes. Usei a licença acadêmica da Gurobi para trabalhar com cadeia de suprimentos. Problemas que levavam minutos com o SciPy resolvidos em segundos.

O PuLP é o meu Python preferido. Ele oferece uma API simples para criar modelos resolvidos por vários backends:

from pulp import *

model = LpProblem("my_problem", LpMaximize)

x = LpVariable("x", lowBound=0)
y = LpVariable("y", lowBound=0)

model += 3*x + 2*y
model += x + y <= 100
model += 2*x + y <= 150

model.solve()

print(f"Used solver: {model.solver}")
print(f"Status: {LpStatus[model.status]}")

A camada de abstração significa um código independente do solucionador que funciona em diferentes sistemas. O Pyomo tem recursos mais avançados para otimização complexa, incluindo programação não linear e estocástica.

Alternativas em nuvem e de código aberto

As nuvem oferecem otimização como serviço para problemas irregulares em grande escala. Você envia os dados do problema e recebe as soluções por meio da API. A arquitetura sem servidor é elegante, mas mais lenta do que os solucionadores locais para problemas pequenos.

O GLPK (GNU Linear Programming Kit) é um programa de código aberto super confiável. Eu uso isso pra dar aula e pra projetos pessoais. O HiGHS é um solucionador mais recente que tem um desempenho incrível. O SciPy recentemente adotou o HiGHS como seu backend padrão, e meus benchmarks mostraram que ele se equipara ao Gurobi em muitos problemas.

Exemplos de Programação Linear

Trabalhar com exemplos completos ajuda a entender melhor do que só a teoria.

Exemplo 1: Problema de dieta

O problema clássico da dieta é minimizar os custos e, ao mesmo tempo, atender às necessidades nutricionais:

from pulp import *

foods = {
    'Oatmeal': {'cost': 0.50, 'calories': 110, 'protein': 4, 'vitamin': 2},
    'Chicken': {'cost': 2.50, 'calories': 250, 'protein': 30, 'vitamin': 0},
    'Eggs':    {'cost': 0.80, 'calories': 155, 'protein': 13, 'vitamin': 1},
    'Milk':    {'cost': 1.20, 'calories': 150, 'protein': 8, 'vitamin': 4},
    'Bread':   {'cost': 0.30, 'calories': 80, 'protein': 3, 'vitamin': 0}
}

min_calories, min_protein, min_vitamin = 2000, 50, 10

model = LpProblem("Diet_Optimization", LpMinimize)
servings = LpVariable.dicts("servings", foods.keys(), lowBound=0)

model += lpSum([foods[f]['cost'] * servings[f] for f in foods])
model += lpSum([foods[f]['calories'] * servings[f] for f in foods]) >= min_calories
model += lpSum([foods[f]['protein'] * servings[f] for f in foods]) >= min_protein
model += lpSum([foods[f]['vitamin'] * servings[f] for f in foods]) >= min_vitamin

model.solve()

print(f"Total cost: ${value(model.objective):.2f}")
for food in foods:
    if servings[food].varValue > 0.01:
        print(f"{food}: {servings[food].varValue:.2f} servings")

A fórmula acima encontra a combinação mais barata de alimentos que atendem às necessidades nutricionais diárias. Isso mostra que as soluções LP ideais nem sempre são práticas sem restrições adicionais de variedade, gosto ou preferências alimentares.

Essa mesma estrutura também pode servir como base para decisões comerciais, como otimizar cronogramas de produção ou alocar orçamentos de marketing.

Exemplo 2: Planejamento multipériodo

O planejamento multipériodo analisa como os níveis de estoque afetam as necessidades futuras em vários períodos de tempo:

days = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']

centers = {
    'North': {'daily_demand': [100, 80, 90, 110, 85], 'capacity': 250},
    'South': {'daily_demand': [120, 100, 95, 105, 130], 'capacity': 300},
}

delivery_cost = {'Monday': 50, 'Tuesday': 50, 'Wednesday': 50,
                 'Thursday': 50, 'Friday': 70}

model = LpProblem("Multiperiod_Routing", LpMinimize)

deliveries = LpVariable.dicts("deliver",
                              [(c, d) for c in centers for d in days],
                              lowBound=0)
inventory = LpVariable.dicts("inventory",
                            [(c, d) for c in centers for d in days],
                            lowBound=0)

model += lpSum([delivery_cost[d] * deliveries[c, d] 
                for c in centers for d in days])

for c in centers:
    for i, day in enumerate(days):
        if i == 0:
            model += inventory[c, day] == deliveries[c, day] - centers[c]['daily_demand'][i]
        else:
            prev_day = days[i-1]
            model += (inventory[c, day] == inventory[c, prev_day] + 
                     deliveries[c, day] - centers[c]['daily_demand'][i])
        model += inventory[c, day] <= centers[c]['capacity']

model.solve()

Os modelos multipériodos aumentam o tamanho do problema, mas permitem uma otimização sofisticada. O modelo junta as entregas nos dias mais baratos, usando a capacidade de armazenamento para diminuir os custos gerais.

Programação mista inteira

Muitos problemas envolvem decisões específicas: construir uma instalação ou não, designar um funcionário ou não. Isso precisa de programação mista inteira (MIP), que é uma extensão da programação linear com variáveis inteiras e binárias.

Introdução e branch-and-bound

Problemas de roteamento precisam de decisões inteiras. A variável binária x[i][j] mostra se o veículo i vai ao local j. Os veículos não podem fazer visitas parciais.

O método Branch-and-bound procura sistematicamente um espaço de solução discreto resolvendo relaxamentos LP contínuos:

from pulp import *

model_continuous = LpProblem("Continuous", LpMaximize)
x_cont = LpVariable("x", lowBound=0)
y_cont = LpVariable("y", lowBound=0)

model_continuous += 3*x_cont + 4*y_cont
model_continuous += x_cont + 2*y_cont <= 10
model_continuous += 2*x_cont + y_cont <= 12

model_continuous.solve()
print(f"Continuous: x={x_cont.varValue:.2f}, y={y_cont.varValue:.2f}")

model_integer = LpProblem("Integer", LpMaximize)
x_int = LpVariable("x", lowBound=0, cat='Integer')
y_int = LpVariable("y", lowBound=0, cat='Integer')

model_integer += 3*x_int + 4*y_int
model_integer += x_int + 2*y_int <= 10
model_integer += 2*x_int + y_int <= 12

model_integer.solve()
print(f"Integer: x={x_int.varValue:.0f}, y={y_int.varValue:.0f}")

A solução inteira é diferente do arredondamento da solução contínua. O método Branch-and-bound encontra a solução inteira ideal, mas com um custo computacional bem mais alto.

Quando usar programação inteira

Use variáveis inteiras quando as decisões forem naturalmente discretas: abrir instalações, designar funcionários, planejar rotas de veículos. As otimizações no mercado de títulos muitas vezes precisam de soluções mistas inteiras. Variáveis contínuas podem gerar atribuições fracionárias sem sentido, enquanto variáveis binárias produzem soluções que podem ser implementadas.

Mas a programação inteira é bem mais cara. Problemas com centenas de variáveis inteiras podem levar horas, em vez de segundos, para LPs contínuos. Se as quantidades de produção forem grandes, a integralidade importa menos, já que o arredondamento quase não afeta as soluções. Sempre resolva primeiro o relaxamento contínuo para verificar os limites antes de se comprometer com a programação inteira completa.

Conclusão

A programação linear muda a forma como você encara os problemas de otimização. A mesma estrutura matemática se aplica a áreas bem diferentes, desde roteamento até planejamento de produção e gestão de portfólio.

Comece com problemas simples de duas variáveis que você possa visualizar geometricamente. Use o simplex básico pra entender o que os solucionadores comerciais fazem nos bastidores. Trabalhe com formulações reais, transformando os requisitos comerciais em restrições matemáticas.

Para aprofundar seus conhecimentos, explore nossos cursos Introdução à Otimização em Python e Álgebra Linear para Ciência de Dados para fortalecer suas bases matemáticas. Nosso programa de Cientista de machine learning em Python é outra ótima opção.