Régression de Poisson : Une façon de modéliser les données de comptage

Lors de l'analyse de données qui impliquent le comptage d'événements - comme le nombre de plaintes de clients par jour, d'admissions à l'hôpital par mois ou de clics sur un site web par heure - la régression linéaire ordinaire produit souvent des résultats trompeurs. Les données de comptage présentent des caractéristiques uniques qui nécessitent des approches de modélisation spécialisées.

La régression de Poisson est une méthode statistique spécialement conçue pour les données de comptage. Contrairement à la régression linéaire, qui peut prédire des valeurs négatives, la régression de Poisson garantit que les prédictions restent des nombres entiers non négatifs. Il est donc particulièrement utile dans tous les domaines où le comptage des événements est essentiel à la prise de décision.

Si vous êtes novice en matière d'analyse de régression, notre cours Introduction à la régression dans R fournit les concepts fondamentaux dont vous aurez besoin pour ce tutoriel. Pour ceux qui sont prêts à explorer la famille plus large des techniques de régression, Generalized Linear Models in R offre une couverture complète du cadre statistique qui inclut la régression de Poisson.

Comprendre les données de comptage et leurs défis

Ce qui fait la spécificité des données de comptage

Les données de comptage représentent le nombre de fois qu'une chose se produit au cours d'une période ou d'un espace donné. Il peut s'agir, par exemple, du nombre de demandes d'indemnisation déposées par police et par an ou du nombre d'accidents de la route à un carrefour et par mois.

Les données de comptage présentent plusieurs propriétés particulières qui rendent la régression linéaire ordinaire inappropriée :

• Les entiers non négatifs seulement: Les nombres ne peuvent pas être négatifs ou fractionnaires. 
• Distribution asymétrique: La plupart des ensembles de données de comptage présentent de nombreuses valeurs faibles avec des valeurs élevées occasionnelles, créant ainsi une queue droite caractéristique.
• La variance augmente avec la moyenne: Plus le nombre moyen d'échantillons est élevé, plus la variabilité augmente. 

Pourquoi la régression linéaire échoue-t-elle ?

Envisagez de prévoir le nombre de réclamations des clients en fonction de facteurs tels que la complexité du produit et les taux de satisfaction de la clientèle. La régression linéaire traite cette question comme n'importe quel résultat continu, prédisant potentiellement des valeurs impossibles comme -1,5 plaintes ou 14,7 plaintes.

Plus problématique encore, la régression linéaire suppose une variance constante entre tous les niveaux de prédiction. En réalité, les semaines au cours desquelles le nombre de plaintes prévues est plus élevé présenteront probablement une plus grande variabilité que les semaines au cours desquelles le nombre de plaintes prévues est faible. Ce modèlen, appelé hétéroscédasticité, conduit à des intervalles de confiance et à des tests d'hypothèse peu fiables.

Les fondements de la distribution de Poisson

La régression de Poisson s'appuie sur la distribution de probabilité de Poisson, qui décrit naturellement les données de comptage. La distribution de Poisson a un seul paramètre (lambda) qui représente à la fois la moyenne et la variance des comptages. Cette propriété d'égalité de la moyenne-variance, appelée équidispersion, est une hypothèse clé que nous devrons vérifier dans la pratique.

La distribution excelle dans la modélisation d'événements "rares" - pas nécessairement peu fréquents, mais des événements dont chaque occurrence est indépendante et dont le taux reste relativement constant dans des conditions similaires.

Quand utiliser la régression de Poisson

Tout d'abord, parlons des conditions idéales dans lesquelles la régression de Poisson donne de bons résultats. Ensuite, nous pourrons parler des applications réelles. 

Scénarios idéaux

La régression de Poisson fonctionne mieux lorsque vos données remplissent plusieurs conditions :

• Manifestations indépendantes: Chaque événement n'influence pas les autres. Un sinistre ne rend pas un autre plus ou moins probable (en supposant qu'il n'y ait pas de fraude).
• Taux constant: Dans des conditions similaires, le taux moyen d'événements reste stable. Les visites aux urgences peuvent varier selon le jour de la semaine, mais les mardis de mois similaires devraient présenter des tendances cohérentes.
• Cadre temporel ou spatial approprié: Les événements sont comptés sur des périodes ou des zones clairement définies. L'expression "plaintes par mois" est préférable à l'expression "plaintes parfois comptabilisées quotidiennement, parfois hebdomadairement".
• Pas de zéros excédentaires évidents: Bien que certains zéros soient attendus, si vos données comportent beaucoup plus de zéros que ne le prévoit la distribution de Poisson, vous pourriez avoir besoin de modèles spécialisés à zéros gonflés.

Applications courantes

Dans le domaine des soins de santé et de l'épidémiologie, les chercheurs suivent les cas de maladie dans des régions ou des périodes données, en tenant compte de la population. Par exemple, ils peuvent étudier l'influence des taux de vaccination sur le nombre d'infections pour 100 000 personnes.

Dans le domaine des affaires et du marketing, les équipes examinent le comportement des clients, comme la fréquence des achats, les tickets d'assistance ou l'engagement. Les entreprises de commerce électronique modélisent souvent les commandes quotidiennes en fonction des dépenses de marketing, de la saisonnalité et des promotions.

Ou voici un exemple courant souvent mentionné avec la régression de Poisson : Les équipes de fabrication surveillent les taux de défauts par taille de lot ou par période d'inspection afin de détecter rapidement les problèmes de qualité et d'améliorer les processus.

Comprendre la structure et les hypothèses du modèle

La connexion log-link

La régression de Poisson ne modélise pas directement les effectifs. Au lieu de cela, il modélise le logarithme du nombre attendu comme une combinaison linéaire de prédicteurs.

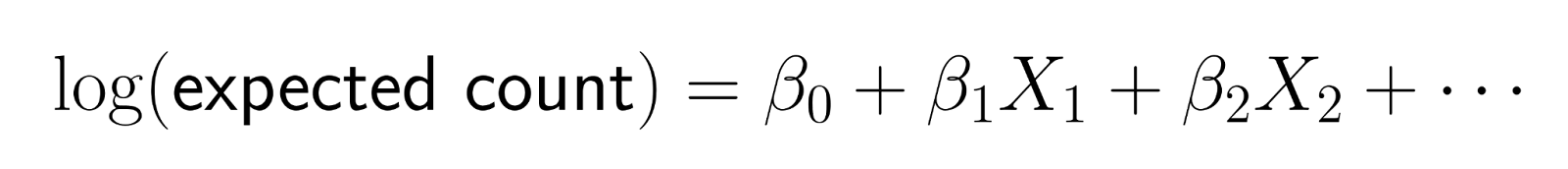
Cette transformation logarithmique garantit que les prévisions restent positives. Plus précisément, la fonction log-link transforme le nombre attendu en échelle logarithmique, garantissant que les prévisions du modèle pour le nombremoyen de restent strictement positives. Lorsque nous inversons la transformation (en exponentialisant), nous obtenons :

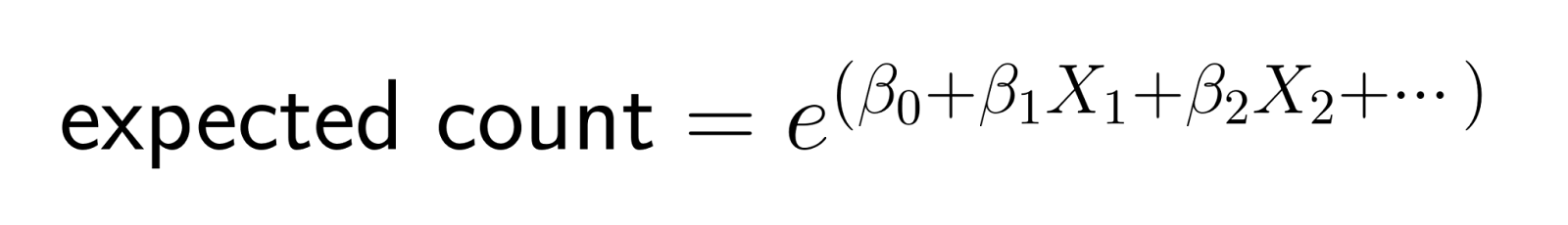
Cette structure signifie que les changements dans les prédicteurs ont des effets multiplicatifs sur le nombre attendu. 

Interprétation des effets multiplicatifs

Dans la régression linéaire, l'augmentation d'une unité d'un prédicteur ajoute une quantité constante au résultat. Dans la régression de Poisson, l'augmentation d'un prédicteur d'une unité multiplie le nombre attendu par un facteur constant.

Par exemple, si le coefficient des "dépenses de marketing" est de 0,1, chaque dollar supplémentaire de dépenses de marketing multiplie le nombre attendu de clients par e^0,1 ≈ 1,105, ce qui représente une augmentation d'environ 10,5 %.

Même si elle semble plus compliquée, cette caractéristique peut être intuitive pour les applications commerciales, où l'on pense souvent en termes de variations en pourcentage et d'effets relatifs.

Hypothèses clés à vérifier

Comme pour tout modèle, il faut faire attention à certaines hypothèses : 

• Indépendance: Les observations ne doivent pas s'influencer mutuellement. Si vous analysez des comptages quotidiens au fil du temps, des schémas temporels marqués peuvent indiquer une dépendance nécessitant une modélisation plus sophistiquée.
• Equidispersion: La variance doit être approximativement égale à la moyenne. Calculez ce ratio pour vos données - des valeurs très supérieures à 1 suggèrent une surdispersion qui doit être corrigée.
• Forme fonctionnelle correcte: La relation entre les variables prédictives et le log-compte doit être à peu près linéaire. Les relations non linéaires peuvent nécessiter des termes polynomiaux ou des transformations.
• Pas de valeurs aberrantes graves: Des valeurs de comptage extrêmes peuvent influencer les résultats de manière disproportionnée. Déterminez si les valeurs aberrantes représentent des erreurs de données ou de véritables événements extrêmes.

Travailler avec l'exposition et les décalages

Comprendre les variables d'exposition

De nombreux ensembles de données de comptage impliquent différents niveaux d'exposition - périodes de temps, tailles de population ou intensités d'observation variables. Par exemple, pour comparer le nombre d'accidents dans différentes villes, il faut tenir compte des différences de population, ou pour comparer des chiffres de vente mensuels, il faut tenir compte du fait que certains mois ne comptent pas le même nombre de jours.

Les variables d'exposition représentent le "dénominateur" qui permet de comparer les chiffres. Sans ajustement approprié, les grandes villes auront trivialement plus d'accidents, et les mois plus longs auront des ventes plus élevées, ce qui risque de masquer les véritables relations que vous souhaitez étudier.

Mise en œuvre des compensations

Les compensations permettent d'incorporer des variables d'exposition dont le coefficient est fixé à 1. Au lieu de modéliser des comptages bruts, les décalages vous permettent de modéliser des taux tout en conservant la structure de comptage de vos données.

La forme mathématique est la suivante :

En réarrangeant cette équation :

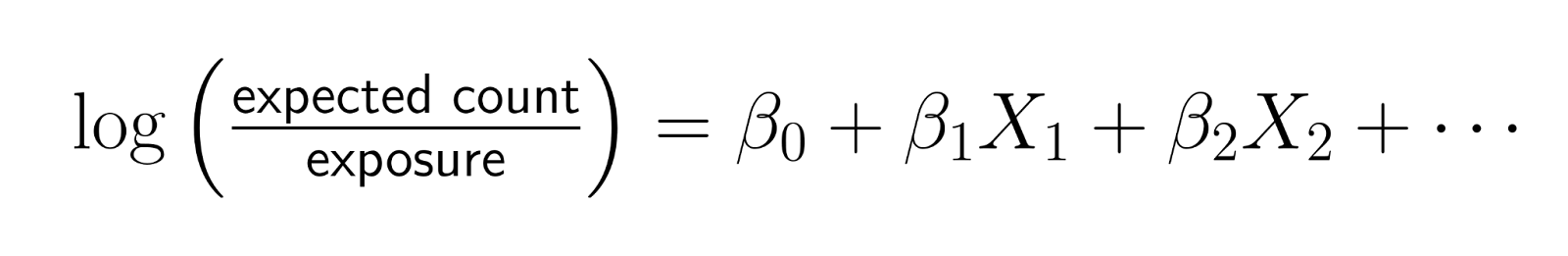
Cela montre que vous modélisez effectivement le logarithme du taux, où le taux = comptage/exposition.

Quand cette réflexion est utile

• Taux de maladie ajustés à la population: Lorsque vous comparez le nombre de cas COVID-19 entre les comtés, incluez le log(population) comme compensation. De cette manière, les coefficients représentent les effets sur les cas par personne plutôt que sur le nombre total de cas.
• Mesures commerciales ajustées dans le temps: Si vous analysez des ventes mensuelles avec certains mois ayant des périodes promotionnelles différentes, incluez log(promotional_days) comme compensation pour étudier les ventes par jour de promotion.
• Données environnementales ajustées à la superficie: Lorsque vous comptez les observations d'espèces dans différentes parcelles d'habitat, incluez log(area_surveyed) comme compensation pour modéliser la densité des espèces plutôt que les comptages bruts.

Le décalage garantit que le doublement de l'exposition double le nombre attendu (toutes choses égales par ailleurs), ce qui est la relation naturelle pour les phénomènes basés sur le taux.

Interprétation des coefficients et des résultats

Des coefficients aux taux d'incidence

Les coefficients bruts de régression de Poisson représentent des changements dans le logarithme de l'effectif, ce qui peut être difficile à interpréter directement. L'exponentialisation des coefficients les transforme en ratios de taux d'incidence (IRR), qui ont une interprétation intuitive.

Un TRI représente le changement multiplicatif du nombre attendu pour une augmentation d'une unité du prédicteur :

• TRI = 1,0 : Aucun effet (le prédicteur ne modifie pas le taux)
• TRI = 1,2 : Augmentation de 20 % du taux
• TRI = 0,8 : Diminution de 20 % du taux
• TRI = 2,0 : Augmentation de 100 % (doublement du taux)

Interprétation des différents types de prédicteurs

• Prédicteurs continus: Si l'âge a un TRI de 1,03, chaque année supplémentaire d'âge multiplie le nombre attendu par 1,03, ce qui représente une augmentation de 3 %. Pour une différence d'âge de 10 ans, l'effet serait de 1,03^10 ≈ 1,34, soit une augmentation d'environ 34 %.
• Prédicteurs binaires: Si le sexe (homme ou femme) a un TRI de 1,5, les hommes ont un taux de réussite 1,5 fois supérieur à celui des femmes, soit un taux 50 % plus élevé.
• Prédicteurs catégoriels: Dans le cas de catégories multiples, chaque niveau est comparé à une catégorie de référence. Si l'"hiver" a un TRI de 0,7 par rapport à l'"été", les mois d'hiver présentent 30 % d'événements en moins que les mois d'été.

Comprendre les intervalles de confiance

Les intervalles de confiance du TRI fournissent des estimations de l'incertitude autour de vos ratios de taux. Un TRI de 1,25 avec un intervalle de confiance à 95 % de [1,10, 1,42] suggère que vous pouvez être raisonnablement sûr que l'effet réel représente entre 10 % et 42 % d'augmentation du taux.

Si un intervalle de confiance comprend 1,0, l'effet peut ne pas être statistiquement significatif. Par exemple, un IRR de 1,15 avec un IC de [0,95, 1,39] suggère que le prédicteur pourrait n'avoir aucun effet.

Stratégies de communication pratiques

Lorsque vous présentez des résultats à un public non technique, mettez l'accent sur les variations en pourcentage plutôt que sur les ratios. Au lieu de dire "le TRI est de 1,3", dites "ce facteur est associé à une augmentation de 30 % du taux d'événements".

Donnez des exemples concrets : "D'après notre modèle, une augmentation des dépenses de marketing de 1 000 dollars est associée à une augmentation d'environ 15 % des acquisitions de clients, qui passent d'une moyenne de 20 à environ 23 clients par mois."

Mise en œuvre de la régression de Poisson dans R

Maintenant que nous avons passé en revue les détails de l'interprétation, mettons en œuvre R.

Préparation et exploration des données

Avant de procéder à l'ajustement d'un modèle, examinez soigneusement vos données de comptage. Commencez par charger les bibliothèques nécessaires et explorez la distribution :

library(ggplot2)
library(dplyr)

# Example: Website daily visitor counts
data <- data.frame(
  visitors = c(42, 48, 39, 52, 44, 58, 51, 47, 41, 49, 40, 46, 43, 54, 50),
  day_of_week = factor(c("Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun",
                        "Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun", "Mon")),
  marketing_spend = c(200, 150, 180, 250, 220, 400, 350, 300, 160, 190,
                     140, 210, 380, 420, 170),
  temperature = c(22, 25, 19, 24, 26, 28, 30, 27, 21, 23, 18, 25, 29, 31, 20)
)

# Check mean vs variance (should be similar for Poisson)
mean(data$visitors)
var(data$visitors)
var(data$visitors) / mean(data$visitors) # Should be close to 1

# Visualize the distribution
ggplot(data, aes(x = visitors)) +
  geom_histogram(bins = 8, fill = "lightblue", color = "black") +
  labs(title = "Distribution of Daily Visitors",
       x = "Number of Visitors", y = "Frequency")

> mean(data$visitors)
[1] 46.93333
> var(data$visitors)
[1] 30.35238
> var(data$visitors) / mean(data$visitors)
[1] 0.6467127

Le rapport variance/moyenne de 0,65 est raisonnablement proche de 1, ce qui indique que nos données sont bien adaptées à la régression de Poisson. Bien qu'ils ne soient pas exactement égaux, les rapports entre 0,5 et 1,5 sont généralement acceptables et suggèrent que la distribution de Poisson constitue une bonne base pour la modélisation de ces données de comptage.

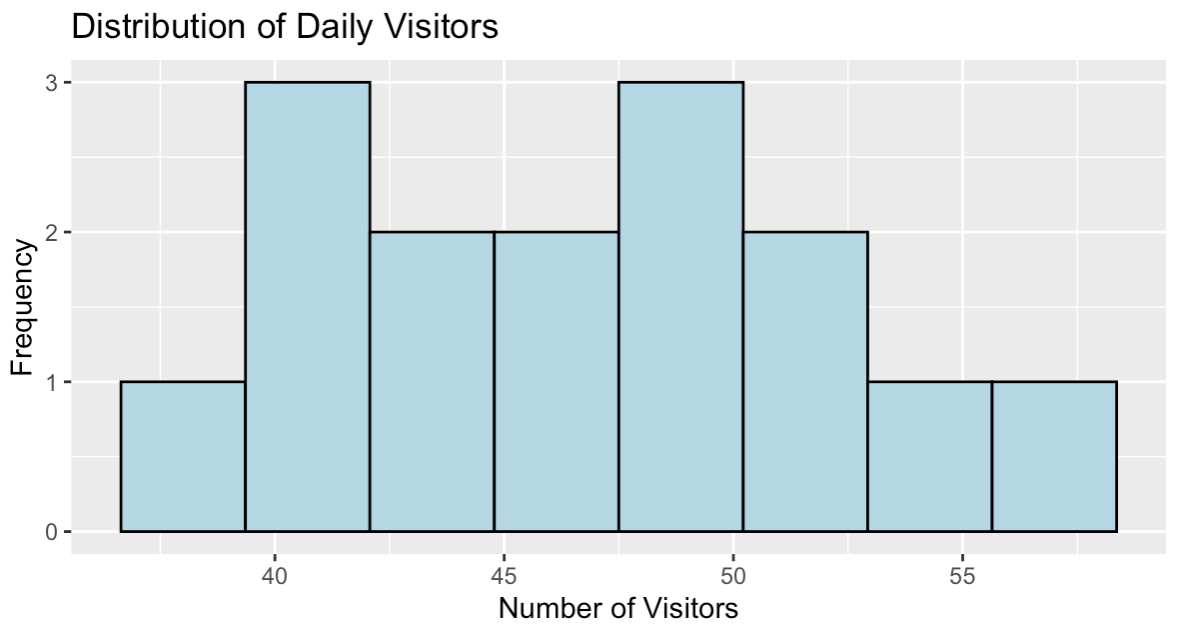
Répartition des visiteurs quotidiens du site web. Image par l'auteur.

L'histogramme montre une distribution à peu près symétrique du nombre de visiteurs, centrée autour de 47 visiteurs par jour, avec des valeurs allant de 39 à 58 environ. Ce modèle de distribution est cohérent avec les données de comptage qui peuvent être modélisées efficacement à l'aide de la régression de Poisson.

Ajustement du modèle

La fonction glm() avec family = poisson ajuste les modèles de régression de Poisson :

# Basic Poisson regression
model <- glm(visitors ~ day_of_week + marketing_spend + temperature,
             family = poisson, data = data)

# View key model results
summary(model)

# Calculate Incidence Rate Ratios (IRRs)
exp(coefficients(model))

Voici le tableau des coefficients :

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)    
(Intercept)     3.2978122  0.5556601   5.935 2.94e-09 ***
day_of_weekMon  0.0724036  0.1635467   0.443    0.658    
day_of_weekSat  0.0316265  0.2872878   0.110    0.912    
day_of_weekSun  0.0339621  0.2502578   0.136    0.892    
day_of_weekThu  0.1068756  0.1870821   0.571    0.568    
day_of_weekTue  0.0442967  0.1633032   0.271    0.786    
day_of_weekWed  0.0653789  0.1813230   0.361    0.718    
marketing_spend 0.0001593  0.0018211   0.087    0.930    
temperature     0.0186099  0.0317682   0.586    0.558

Voici les ratios de taux d'incidence (IRR) :

(Intercept)  day_of_weekMon  day_of_weekSat  day_of_weekSun  day_of_weekThu  day_of_weekTue  day_of_weekWed marketing_spend 
27.053386        1.075089        1.032132        1.034545        1.112796        1.045292        1.067563        1.000159 
temperature 
1.018784 

Les coefficients montrent les effets de l'échelle logarithmique, mais les TRI fournissent des interprétations plus intuitives. Par exemple, le jeudi (day_of_weekThu) a un TRI de 1,11, suggérant environ 11 % de visiteurs en plus par rapport au vendredi (la catégorie de référence). Les dépenses de marketing ont un TRI de 1,0002, ce qui signifie que chaque dollar supplémentaire augmente le nombre de visiteurs attendus d'environ 0,02 %.

Remarquez que si nous calculions les intervalles de confiance pour ces TRI, nombre d'entre eux incluraient 1,0, ce qui suggère que les effets ne sont pas statistiquement significatifs avec ce petit échantillon. Ce phénomène est courant dans les petits ensembles de données et montre pourquoi la taille de l'échantillon est importante.

Inclure l'exposition avec les compensations

Si vos données présentent des périodes d'exposition variables, incluez-les en tant que décalages :

# Example with exposure data
data$exposure_days <- c(rep(7, 10), rep(6, 5))  # Some weeks had 6 observation days

# Model with offset
model_offset <- glm(visitors ~ day_of_week + marketing_spend + temperature + 
                   offset(log(exposure_days)), 
                   family = poisson, data = data)

summary(model_offset)

Call:
glm(formula = visitors ~ day_of_week + marketing_spend + temperature + 
    offset(log(exposure_days)), family = poisson, data = data)

Coefficients:
                  Estimate Std. Error z value Pr(>|z|)   
(Intercept)      1.734e+00  5.579e-01   3.109  0.00188 **
day_of_weekMon   2.371e-02  1.637e-01   0.145  0.88485   
day_of_weekSat   9.873e-02  2.898e-01   0.341  0.73338   
day_of_weekSun   1.208e-01  2.472e-01   0.489  0.62513   
day_of_weekThu   5.642e-02  1.871e-01   0.302  0.76297   
day_of_weekTue  -6.713e-02  1.634e-01  -0.411  0.68128   
day_of_weekWed  -6.073e-02  1.825e-01  -0.333  0.73934   
marketing_spend -4.231e-05  1.823e-03  -0.023  0.98149   
temperature      8.210e-03  3.179e-02   0.258  0.79623

Remarquez que les coefficients changent radicalement lorsque nous incluons le décalage. L'ordonnée à l'origine passe de 3,30 à 1,73 et tous les autres effets deviennent plus faibles. Cette transformation s'explique par le fait que nous modélisons désormais le taux journalier plutôt que le nombre total de personnes sur des périodes variables.

Le décalage assure des comparaisons équitables en ajustant les différentes longueurs d'exposition. Sans cet ajustement, les périodes comportant un plus grand nombre de jours d'observation sembleraient artificiellement avoir un nombre de visiteurs plus élevé, ce qui pourrait masquer les véritables relations que nous voulons étudier. Le modèle répond désormais à la question "Quel est le taux de fréquentation quotidien ?" plutôt qu'à la question "Combien y a-t-il eu de visiteurs au total ?".

Faire des prévisions

Générer des prédictions pour de nouveaux scénarios :

# Create new data for prediction
new_data <- data.frame(
  day_of_week = factor("Fri", levels = levels(data$day_of_week)),
  marketing_spend = 300,
  temperature = 25
)

# Predict expected counts
predicted_counts <- predict(model, newdata = new_data, type = "response")
print(paste("Expected visitors:", round(predicted_counts, 1)))

[1] "Expected visitors: 45.2"

Le modèle prévoit 45,2 visiteurs pour un vendredi avec des dépenses de marketing de 300 $ et une température de 25°C. Cette prévision se situe dans la fourchette raisonnable de nos données observées (39-58 visiteurs) et est proche de notre moyenne générale de 46,9 visiteurs.

La régression de Poisson garantit naturellement que les prédictions restent des nombres entiers positifs lorsqu'elles sont arrondies, contrairement à la régression linéaire qui pourrait produire des valeurs négatives impossibles à obtenir. Le paramètre type = "response" renvoie les prédictions sur l'échelle de comptage originale plutôt que sur l'échelle logarithmique utilisée en interne par le modèle.

Diagnostics essentiels du modèle

Vérification de la surdispersion

Il y a surdispersion lorsque la variance est supérieure à la moyenne, ce qui constitue une violation de l'hypothèse clé de Poisson :

# Calculate dispersion statistic
residual_deviance <- model$deviance
df_residual <- model$df.residual
dispersion <- residual_deviance / df_residual

print(paste("Dispersion statistic:", round(dispersion, 3)))

if (dispersion > 1.5) {
  print("Possible overdispersion detected")
  print("Consider quasi-Poisson or negative binomial models")
}

[1] "Dispersion statistic: 0.849"

La statistique de dispersion de 0,849 est proche de 1, ce qui indique que notre modèle s'ajuste bien aux données sans surdispersion significative. Les valeurs proches de 1 suggèrent que l'hypothèse de Poisson, avec une moyenne et une variance égales, est raisonnable pour cet ensemble de données.

Comme la statistique est inférieure à 1,5, aucun message d'avertissement n'apparaît, ce qui confirme que la régression de Poisson standard est appropriée. Si cette valeur était beaucoup plus grande que 1 (généralement supérieure à 1,5), nous devrions envisager des modèles quasi-Poisson ou binomiaux négatifs pour tenir compte de la variabilité supplémentaire.

Analyse résiduelle

Examinez les résidus pour détecter les tendances ou les violations du modèle :

# Calculate Pearson residuals
fitted_values <- fitted(model)
pearson_residuals <- residuals(model, type = "pearson")

# Plot residuals vs fitted values
plot(fitted_values, pearson_residuals,
     xlab = "Fitted Values", ylab = "Pearson Residuals",
     main = "Residuals vs Fitted")
abline(h = 0, col = "red", lty = 2)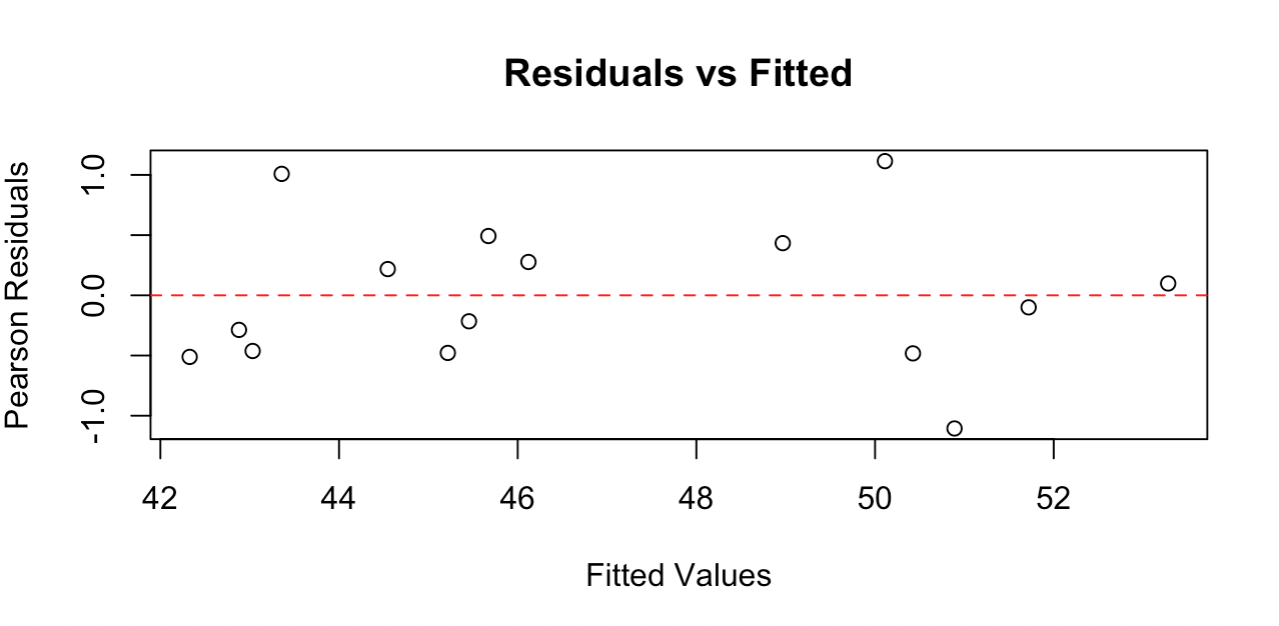

Graphique des résidus montrant une dispersion aléatoire autour de zéro. Image par l'auteur.

Le graphique des résidus montre des points dispersés au hasard autour de la ligne du zéro, sans schéma clair, ce qui indique que notre modèle s'adapte bien aux données. Les résidus se situent approximativement entre -1 et +1, ce qui est raisonnable pour cette taille d'échantillon.

Un bon graphique des résidus doit montrer : une dispersion aléatoire autour de zéro (pas de courbes), une dispersion à peu près constante des valeurs ajustées (pas de forme d'entonnoir) et pas de valeurs extrêmes aberrantes. Ce graphique répond à tous ces critères, confirmant que les hypothèses de la régression de Poisson sont satisfaites et que notre modèle fournit des résultats fiables.

Traitement de la surdispersion

Si une surdispersion est détectée, envisagez des modèles de quasi-Poisson qui ajustent les erreurs standard :

# Fit quasi-Poisson model
quasi_model <- glm(visitors ~ day_of_week + marketing_spend + temperature, 
                   family = quasipoisson, data = data)

Comme notre modèle présente une bonne dispersion (0,849), les ajustements quasi-Poisson ne sont pas nécessaires ici. Toutefois, cette approche fournit des intervalles de confiance et des valeurs p plus prudents lorsque la variance dépasse la moyenne, ce qui en fait un outil précieux pour les données de comptage du monde réel qui présentent souvent une surdispersion.

Présentation et interprétation des résultats

Créer des résumés clairs des résultats

Transformez les résultats du modèle en informations pertinentes pour l'entreprise en vous concentrant sur la signification pratique de vos TRI. Lorsque votre modèle montre que les jours de week-end ont un TRI de 1,4 par rapport aux jours de semaine, communiquez cette information en disant que les week-ends accueillent environ 40 % de visiteurs de plus que les jours de semaine. Lorsque les dépenses de marketing ont un TRI de 1,002, expliquez que "chaque dollar supplémentaire investi dans le marketing est associé à une augmentation d'environ 0,2 % du nombre de visiteurs".

Pour les variables continues, envisagez de présenter les effets à des intervalles significatifs. Au lieu de discuter de l'effet d'un changement de température d'un seul degré, montrez l'impact d'une différence de 10 degrés, qui pourrait être plus pertinente pour la planification des activités.

Comprendre les limites du modèle

La régression de Poisson identifie des associations et non des relations de cause à effet. Une forte association entre les dépenses de marketing et le nombre de visiteurs ne prouve pas que le marketing est à l'origine de l'augmentation.  D'autres facteurs peuvent influencer ces deux variables. Reconnaissez cette limitation lors de la présentation des résultats.

Le modèle suppose que le taux reste constant pour des valeurs prédictives données. Si votre entreprise connaît des tendances saisonnières qui ne sont pas prises en compte par vos variables, ou si la relation entre les variables prédictives et les résultats évolue dans le temps, votre modèle risque de ne pas bien se généraliser aux périodes futures.

Défis communs et solutions

Traiter les comptes à zéro

Les données de comptage contiennent souvent des zéros, qui sont parfaitement valables dans le cadre d'une régression de Poisson. Toutefois, si vos données comportent beaucoup plus de zéros que ne le prévoirait une distribution de Poisson, cela pourrait indiquer un processus de génération de données différent. Certaines observations peuvent représenter des périodes ou des conditions où l'événement ne peut tout simplement pas se produire, plutôt que des périodes où il aurait pu se produire mais ne l'a pas fait.

Par exemple, le nombre de visiteurs d'un site web peut inclure des zéros pour les jours où le site était indisponible pour des raisons de maintenance. Ces "zéros structurels" sont différents des "zéros aléatoires" qui se produisent naturellement dans les processus de Poisson.

Stratégie de construction de modèles

Commencez par les prédicteurs les plus importants, basés sur la connaissance du domaine. Ajoutez des variables une à une et évaluez si elles améliorent votre compréhension des données. Les modèles plus complexes ne sont pas toujours meilleurs.

Prêtez attention à l'importance pratique des effets, et pas seulement à l'importance statistique. Un changement statistiquement significatif de 1 % dans les taux d'événements peut ne pas justifier une action commerciale, tandis qu'un changement de 20 % qui est marginalement non significatif peut encore justifier une investigation avec plus de données.

Traitement des infractions

Lorsque l'équidispersion échoue (variance beaucoup plus grande que la moyenne), la régression quasi-Poisson offre une solution simple. Il conserve la même structure de modèle mais ajuste les erreurs standard pour tenir compte de la variabilité supplémentaire. Cela permet d'obtenir des intervalles de confiance et des valeurs p plus prudents.

En cas de forte surdispersion, la régression binomiale négative modélise explicitement la variation supplémentaire. Cette approche permet d'estimer à la fois la relation moyenne et la variabilité supplémentaire.

Bonnes pratiques et recommandations

Éviter les erreurs courantes

N'ignorez pas la surdispersion - c'est l'une des violations les plus courantes des hypothèses de Poisson et elle peut sérieusement affecter vos conclusions. Vérifiez toujours le rapport entre la variance et la moyenne et envisagez d'autres solutions si nécessaire.

Soyez prudent lorsque vous extrapolez au-delà de votre plage de données. Si les données relatives à vos dépenses de marketing se situent entre 100 et 1 000 dollars, ne prévoyez pas avec certitude des effets pour des niveaux de dépenses de 5 000 dollars. La relation peut ne pas rester log-linéaire pour les valeurs extrêmes.

Évitez de traiter tous les prédicteurs catégoriels comme ayant un espacement égal entre les niveaux. Les catégories d'éducation (lycée, études supérieures partielles, diplôme d'études supérieures) peuvent ne pas avoir les mêmes effets sur votre variable de résultat.

Documentation et flux de travail

Documentez vos décisions de modélisation, en particulier les violations d'hypothèses et la manière dont vous les avez traitées. Si vous avez découvert une surdispersion mais que vous avez choisi des ajustements quasi-Poisson, notez cette décision et ses implications pour l'interprétation.

Conclusion

La régression de Poisson constitue un cadre efficace pour l'analyse des données de comptage dans de nombreux domaines. Lorsque vous appliquez ces techniques à vos propres données, commencez par des modèles simples et complexifiez-les progressivement en vous basant à la fois sur des preuves statistiques et sur votre expertise dans le domaine. Lorsque les hypothèses ne sont pas respectées, des extensions telles que les modèles quasi-Poisson ou binomial négatif offrent de bonnes alternatives. L'objectif n'est pas seulement d'obtenir une signification statistique, mais aussi d'obtenir des informations pratiques qui permettent de prendre de meilleures décisions.

Si vous souhaitez approfondir votre expertise en matière de régression, notre cours Régression intermédiaire en R couvre des techniques de diagnostic avancées et des stratégies de modélisation qui complètent les compétences en régression de Poisson que vous avez acquises ici. Les modèles linéaires généralisés en R constituent une autre option intéressante.