Regresión de Poisson: Una forma de modelar los datos de recuento

Cuando se analizan datos que implican el recuento de eventos -como el número de reclamaciones de clientes al día, ingresos hospitalarios al mes o clics en el sitio web por hora-, la regresión lineal ordinaria suele producir resultados engañosos. Los datos de recuento tienen características únicas que requieren enfoques de modelización especializados.

La regresión de Poisson es un método estadístico diseñado específicamente para datos de recuento. A diferencia de la regresión lineal, que puede predecir valores negativos, la regresión de Poisson garantiza que las predicciones sigan siendo números enteros no negativos. Esto lo hace especialmente valioso en cualquier campo en el que el recuento de acontecimientos sea fundamental para la toma de decisiones.

Si eres nuevo en el análisis de regresión, nuestro curso Introducción a la regresión en R proporciona los conceptos básicos esenciales que necesitarás para este tutorial. Para quienes estén preparados para explorar la familia más amplia de técnicas de regresión, Modelos lineales generalizados en R ofrece una cobertura exhaustiva del marco estadístico que incluye la regresión de Poisson.

Comprender los Datos Contables y sus Desafíos

Qué hace especiales a los datos de recuento

Los datos de recuento representan el número de veces que ocurre algo en un periodo o espacio determinado. Algunos ejemplos son el número de reclamaciones de seguros presentadas por póliza al año o el número de accidentes de tráfico en una intersección al mes.

Los datos de recuento tienen varias propiedades distintivas que hacen inadecuada la regresión lineal ordinaria:

• Sólo números enteros no negativos: Los recuentos no pueden ser negativos ni fraccionarios. 
• Distribución sesgada a la derecha: La mayoría de los conjuntos de datos de recuento muestran muchos valores bajos con valores altos ocasionales, creando una cola derecha característica.
• La varianza aumenta con la media: A medida que aumentan los recuentos medios, suele aumentar también la variabilidad. 

Por qué falla la regresión lineal

Considera la posibilidad de predecir el número de reclamaciones de los clientes basándote en factores como la complejidad del producto y las puntuaciones de satisfacción del cliente. La regresión lineal trata esto como cualquier resultado continuo, pudiendo predecir valores imposibles como -1,5 quejas o 14,7 quejas.

Y lo que es más problemático, la regresión lineal asume una varianza constante en todos los niveles de predicción. En realidad, es probable que las semanas en las que se prevea un mayor número de reclamaciones muestren más variabilidad que las semanas en las que se prevea un número menor. Este patrónn, llamado heteroscedasticidad, da lugar a intervalos de confianza y pruebas de hipótesis poco fiables.

El fundamento de la distribución de Poisson

La regresión de Po isson se basa en la distribución de probabilidad de Poisson, que describe de forma natural los datos de recuento. La distribución de Poisson tiene un único parámetro (lambda) que representa tanto la media como la varianza de los recuentos. Esta propiedad de igual varianza media, llamada equidispersión, es un supuesto clave que tendremos que verificar en la práctica.

La distribución destaca en el modelado de sucesos "raros", no necesariamente infrecuentes, sino sucesos en los que cada suceso individual es independiente y la tasa permanece relativamente constante en condiciones similares.

Cuándo utilizar la regresión de Poisson

En primer lugar, hablemos de las condiciones ideales en las que la regresión de Poisson funciona bien. Después, podemos hablar de las aplicaciones reales. 

Escenarios ideales

La regresión de Poisson funciona mejor cuando tus datos cumplen varias condiciones:

• Eventos independientes: Cada suceso no influye en los demás. Una reclamación al seguro no hace que otra sea más o menos probable (suponiendo que no haya patrones de fraude).
• Tasa constante: En condiciones similares, la tasa media de acontecimientos permanece estable. Las visitas a urgencias pueden variar según el día de la semana, pero los martes de meses similares deberían mostrar pautas constantes.
• Marco temporal o espacial adecuado: Los eventos se cuentan en periodos o zonas claramente definidos. "Quejas al mes" es mejor que "quejas a veces contadas diariamente, a veces semanalmente".
• No hay exceso evidente de ceros: Aunque algunos ceros son de esperar, si tus datos tienen muchos más ceros de los que predeciría la distribución de Poisson, podrías necesitar modelos especializados de cero inflado.

Aplicaciones comunes

En sanidad y epidemiología, los investigadores hacen un seguimiento de los casos de enfermedad en distintas regiones o periodos de tiempo, ajustándose a la población. Por ejemplo, pueden estudiar cómo influyen las tasas de vacunación en las infecciones por cada 100.000 personas.

En los negocios y el marketing, los equipos examinan el comportamiento de los clientes, como la frecuencia de compra, los tickets de asistencia o el compromiso. Las empresas de comercio electrónico suelen modelar los pedidos diarios en función del gasto en marketing, la estacionalidad y las promociones.

O aquí tienes un ejemplo común que se menciona a menudo con la regresión de Poisson: Los equipos de fabricación controlan las tasas de defectos por tamaño de lote o periodo de inspección para detectar pronto los problemas de calidad y mejorar los procesos.

Comprender la estructura y los supuestos del modelo

La conexión log-link

La regresión de Poisson no modela los recuentos directamente. En su lugar, modela el logaritmo del recuento esperado como una combinación lineal de predictores.

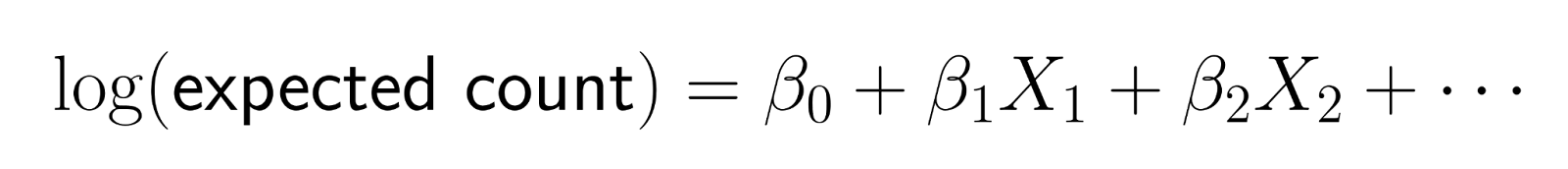
Esta transformación logarítmica, garantiza que las predicciones sigan siendo positivas. En concreto, la función de enlace logarítmico transforma el recuento esperado a la escala logarítmica, garantizando que las predicciones del modelo para el recuentomedio sigan siendo estrictamente positivas. Si invertimos la transformación (exponenciando), obtenemos:

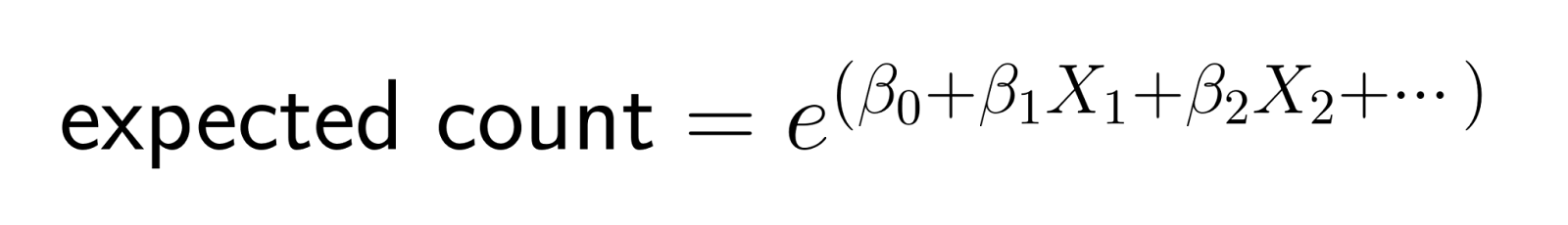
Esta estructura significa que los cambios en los predictores tienen efectos multiplicativos en el recuento esperado. 

Interpretar los efectos multiplicativos

En la regresión lineal, el aumento de un predictor en una unidad añade una cantidad constante al resultado. En la regresión de Poisson, aumentar un predictor en una unidad multiplica el recuento esperado por un factor constante.

Por ejemplo, si el coeficiente del "gasto en marketing" es 0,1, entonces cada dólar adicional de gasto en marketing multiplica el número esperado de clientes por e^0,1 ≈ 1,105, lo que representa aproximadamente un aumento del 10,5%.

Aunque parezca más complicada, esta característica puede ser intuitiva para las aplicaciones empresariales, donde a menudo pensamos en términos de cambios porcentuales y efectos relativos.

Supuestos clave a verificar

Como con cualquier modelo, hay algunos supuestos a los que debemos prestar atención: 

• Independencia: Las observaciones no deben influirse mutuamente. Si estás analizando recuentos diarios a lo largo del tiempo, los patrones temporales fuertes podrían indicar una dependencia que requiera una modelización más sofisticada.
• Equidispersión: La varianza debe ser aproximadamente igual a la media. Calcula esta relación para tus datos: valores muy superiores a 1 sugieren una dispersión excesiva que hay que abordar.
• Forma funcional correcta: La relación entre los predictores y el recuento logarítmico debe ser aproximadamente lineal. Las relaciones no lineales pueden requerir términos polinómicos o transformaciones.
• No hay valores atípicos graves: Los valores de recuento extremos pueden influir desproporcionadamente en los resultados. Investiga si los valores atípicos representan errores en los datos o auténticos sucesos extremos.

Trabajar con Exposición y Desfases

Comprender las variables de exposición

Muchos conjuntos de datos de recuento implican distintos niveles de exposición: distintos periodos de tiempo, tamaños de población o intensidades de observación. Por ejemplo, para comparar los recuentos de accidentes entre ciudades hay que tener en cuenta las diferencias de población, o para comparar las cifras de ventas mensuales hay que tener en cuenta que algunos meses tienen diferente número de días.

Las variables de exposición representan el "denominador" que hace comparables los recuentos. Sin un ajuste adecuado, las ciudades más grandes tendrán trivialmente más accidentes, y los meses más largos tendrán mayores ventas, enmascarando potencialmente las verdaderas relaciones que quieres estudiar.

Aplicación de las compensaciones

Las compensaciones permiten incorporar variables de exposición con un coeficiente fijo a 1. En lugar de modelizar recuentos brutos, los offsets te permiten modelizar tasas manteniendo la estructura de recuento de tus datos.

La forma matemática es

Reordenando esta ecuación:

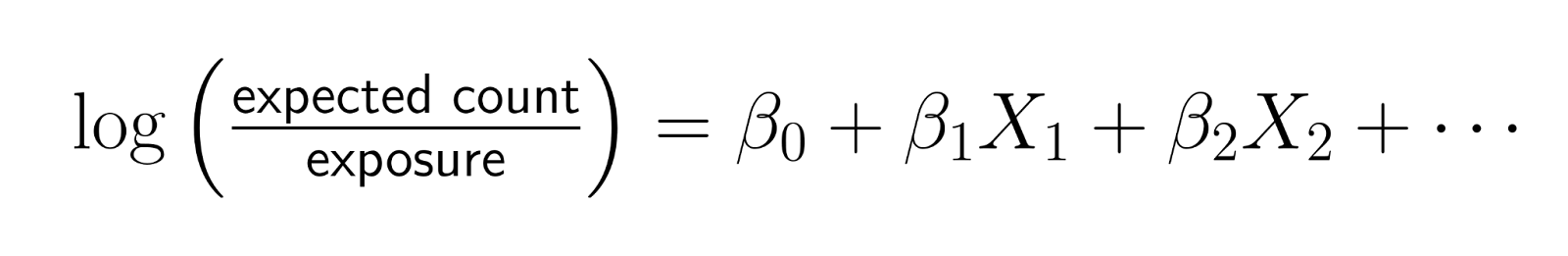
Esto demuestra que estás modelando efectivamente la tasa logarítmica, donde tasa = recuento/exposición.

Cuándo es útil este pensamiento

• Tasas de enfermedad ajustadas a la población: Al comparar los recuentos de casos COVID-19 entre condados, incluye log(población) como compensación. De este modo, los coeficientes representan los efectos sobre los casos por persona y no sobre el total de casos.
• Métricas empresariales ajustadas en el tiempo: Si analizas las ventas mensuales con algunos meses que tienen distintos periodos promocionales, incluye log(días_promocionales) como desplazamiento para estudiar las ventas por día promocional.
• Datos medioambientales ajustados a la zona: Cuando cuentes los avistamientos de especies en distintos parches de hábitat, incluye log(área_explorada) como compensación para modelar la densidad de especies en lugar de los recuentos brutos.

La compensación garantiza que al duplicar la exposición se duplique el recuento esperado (en igualdad de condiciones), que es la relación natural para los fenómenos basados en la tasa.

Interpretación de coeficientes y resultados

De los coeficientes a las tasas de incidencia

Los coeficientes brutos de regresión de Poisson representan cambios en el logaritmo del recuento, que pueden ser difíciles de interpretar directamente. Exponenciando los coeficientes se transforman en tasas de incidencia (TIR), que tienen interpretaciones intuitivas.

Una TIR representa el cambio multiplicativo en el recuento esperado para un aumento de una unidad en el predictor:

• IRR = 1.0: Sin efecto (el predictor no cambia la tasa)
• TIR = 1,2: Aumento del 20% de la tasa
• TIR = 0,8: Disminución del 20% de la tasa
• IRR = 2.0: Aumento del 100% (duplicación de la tasa)

Interpretar los distintos tipos de predictores

• Predictores continuos: Si la edad tiene una TIR de 1,03, cada año adicional de edad multiplica la cuenta esperada por 1,03, lo que representa un aumento del 3%. Para una diferencia de edad de 10 años, el efecto sería de 1,03^10 ≈ 1,34, es decir, aproximadamente un aumento del 34%.
• Predictores binarios: Si el sexo (hombre frente a mujer) tiene una TIR de 1,5, los hombres tienen una tasa 1,5 veces mayor del resultado en comparación con las mujeres, lo que representa una tasa un 50% mayor.
• Predictores categóricos: Con múltiples categorías, cada nivel se compara con una categoría de referencia. Si el "invierno" tiene una TIR de 0,7 en comparación con el "verano", los meses de invierno presentan un 30% menos de sucesos que los meses de verano.

Comprender los intervalos de confianza

Los intervalos de confianza de la TIR proporcionan estimaciones de incertidumbre en torno a tus ratios de tasas. Una TIR de 1,25 con un intervalo de confianza del 95% de [1,10, 1,42] sugiere que puedes estar razonablemente seguro de que el verdadero efecto representa entre un 10% y un 42% de aumento de la tasa.

Si un intervalo de confianza incluye 1,0, puede que el efecto no sea estadísticamente significativo. Por ejemplo, una TIR de 1,15 con IC [0,95, 1,39] sugiere que el predictor podría no tener ningún efecto.

Estrategias prácticas de comunicación

Cuando presentes los resultados a un público no técnico, céntrate en los cambios porcentuales y no en las ratios. En lugar de decir "la TIR es de 1,3", di "este factor está asociado a un aumento del 30% en la tasa de eventos".

Pon ejemplos concretos: "Según nuestro modelo, aumentar el gasto en marketing en 1.000 $ se asocia con aproximadamente un 15% más de adquisiciones de clientes, de una media de 20 a unos 23 clientes al mes".

Implementación de la regresión de Poisson en R

Ahora que hemos repasado los detalles de la interpretación, vamos a implementarla en R.

Preparación y exploración de datos

Antes de ajustar cualquier modelo, examina cuidadosamente tus datos de recuento. Empieza cargando las bibliotecas necesarias y explorando la distribución:

library(ggplot2)
library(dplyr)

# Example: Website daily visitor counts
data <- data.frame(
  visitors = c(42, 48, 39, 52, 44, 58, 51, 47, 41, 49, 40, 46, 43, 54, 50),
  day_of_week = factor(c("Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun",
                        "Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun", "Mon")),
  marketing_spend = c(200, 150, 180, 250, 220, 400, 350, 300, 160, 190,
                     140, 210, 380, 420, 170),
  temperature = c(22, 25, 19, 24, 26, 28, 30, 27, 21, 23, 18, 25, 29, 31, 20)
)

# Check mean vs variance (should be similar for Poisson)
mean(data$visitors)
var(data$visitors)
var(data$visitors) / mean(data$visitors) # Should be close to 1

# Visualize the distribution
ggplot(data, aes(x = visitors)) +
  geom_histogram(bins = 8, fill = "lightblue", color = "black") +
  labs(title = "Distribution of Daily Visitors",
       x = "Number of Visitors", y = "Frequency")

> mean(data$visitors)
[1] 46.93333
> var(data$visitors)
[1] 30.35238
> var(data$visitors) / mean(data$visitors)
[1] 0.6467127

La relación entre la varianza y la media de 0,65 se aproxima razonablemente a 1, lo que indica que nuestros datos se adaptan bien a la regresión de Poisson. Aunque no son exactamente iguales, las proporciones entre 0,5 y 1,5 son generalmente aceptables y sugieren que la distribución de Poisson proporciona una buena base para modelizar estos datos de recuento.

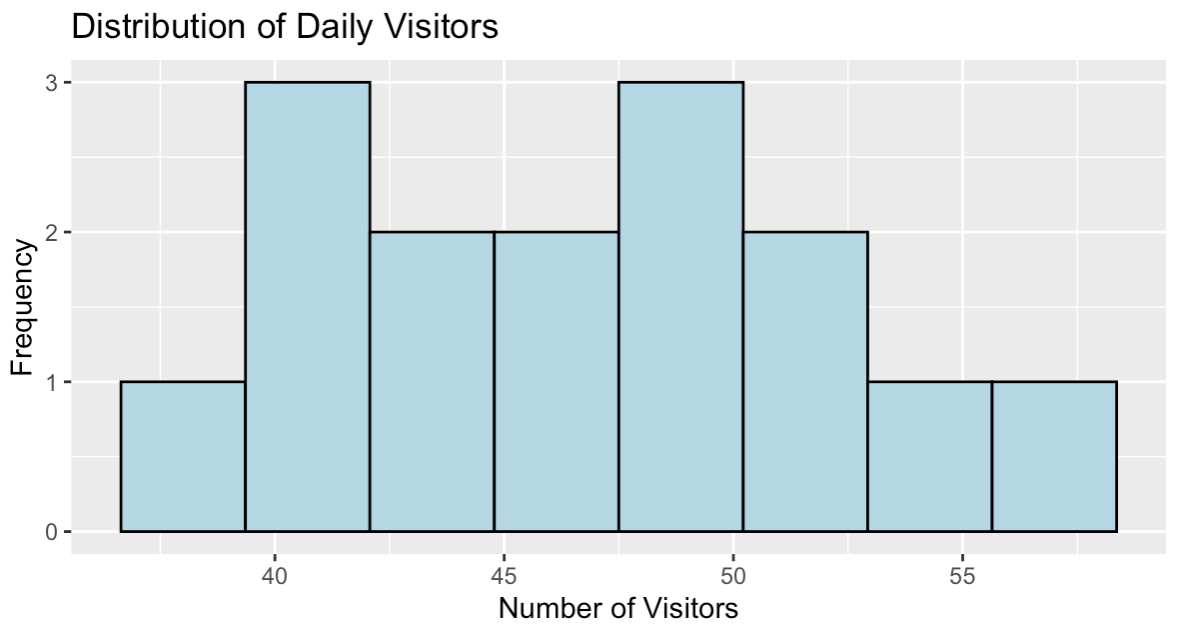
Distribución de los visitantes diarios del sitio web. Imagen del autor.

El histograma muestra una distribución aproximadamente simétrica del recuento de visitantes centrada en 47 visitantes al día, con valores que oscilan entre 39 y 58 aproximadamente. Este patrón de distribución es coherente con los datos de recuento que pueden modelizarse eficazmente mediante la regresión de Poisson.

Ajuste del modelo

La función glm() con family = poisson ajusta modelos de regresión de Poisson:

# Basic Poisson regression
model <- glm(visitors ~ day_of_week + marketing_spend + temperature,
             family = poisson, data = data)

# View key model results
summary(model)

# Calculate Incidence Rate Ratios (IRRs)
exp(coefficients(model))

Aquí tienes la tabla de coeficientes:

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)    
(Intercept)     3.2978122  0.5556601   5.935 2.94e-09 ***
day_of_weekMon  0.0724036  0.1635467   0.443    0.658    
day_of_weekSat  0.0316265  0.2872878   0.110    0.912    
day_of_weekSun  0.0339621  0.2502578   0.136    0.892    
day_of_weekThu  0.1068756  0.1870821   0.571    0.568    
day_of_weekTue  0.0442967  0.1633032   0.271    0.786    
day_of_weekWed  0.0653789  0.1813230   0.361    0.718    
marketing_spend 0.0001593  0.0018211   0.087    0.930    
temperature     0.0186099  0.0317682   0.586    0.558

Aquí tienes las tasas de incidencia (TIR):

(Intercept)  day_of_weekMon  day_of_weekSat  day_of_weekSun  day_of_weekThu  day_of_weekTue  day_of_weekWed marketing_spend 
27.053386        1.075089        1.032132        1.034545        1.112796        1.045292        1.067563        1.000159 
temperature 
1.018784 

Los coeficientes muestran los efectos a escala logarítmica, pero las TIR ofrecen interpretaciones más intuitivas. Por ejemplo, el jueves (day_of_weekThu) tiene una TIR de 1,11, lo que sugiere un 11% más de visitantes en comparación con el viernes (la categoría de referencia). El gasto en marketing tiene una TIR de 1,0002, lo que indica que cada dólar adicional aumenta los visitantes esperados en aproximadamente un 0,02%.

Observa que si calculáramos intervalos de confianza para estas TIR, muchos incluirían 1,0, lo que sugiere que los efectos no son estadísticamente significativos con esta pequeña muestra. Esto es habitual con conjuntos de datos pequeños y demuestra por qué el tamaño de la muestra es importante.

Incluyendo la exposición con compensaciones

Si tus datos tienen periodos de exposición variables, inclúyelos como compensaciones:

# Example with exposure data
data$exposure_days <- c(rep(7, 10), rep(6, 5))  # Some weeks had 6 observation days

# Model with offset
model_offset <- glm(visitors ~ day_of_week + marketing_spend + temperature + 
                   offset(log(exposure_days)), 
                   family = poisson, data = data)

summary(model_offset)

Call:
glm(formula = visitors ~ day_of_week + marketing_spend + temperature + 
    offset(log(exposure_days)), family = poisson, data = data)

Coefficients:
                  Estimate Std. Error z value Pr(>|z|)   
(Intercept)      1.734e+00  5.579e-01   3.109  0.00188 **
day_of_weekMon   2.371e-02  1.637e-01   0.145  0.88485   
day_of_weekSat   9.873e-02  2.898e-01   0.341  0.73338   
day_of_weekSun   1.208e-01  2.472e-01   0.489  0.62513   
day_of_weekThu   5.642e-02  1.871e-01   0.302  0.76297   
day_of_weekTue  -6.713e-02  1.634e-01  -0.411  0.68128   
day_of_weekWed  -6.073e-02  1.825e-01  -0.333  0.73934   
marketing_spend -4.231e-05  1.823e-03  -0.023  0.98149   
temperature      8.210e-03  3.179e-02   0.258  0.79623

Observa cómo cambian drásticamente los coeficientes cuando incluimos el desplazamiento. El intercepto desciende de 3,30 a 1,73, y todos los demás efectos se reducen. Esta transformación se produce porque ahora estamos modelando la tasa por día en lugar de los recuentos totales a lo largo de periodos variables.

El desplazamiento garantiza comparaciones justas ajustándose a las diferentes longitudes de exposición. Sin este ajuste, los periodos con más días de observación parecerían artificialmente tener un mayor número de visitantes, lo que podría enmascarar las verdaderas relaciones que queremos estudiar. El modelo responde ahora "¿Cuál es la tasa diaria de visitantes?" en lugar de "¿Cuántos visitantes totales se produjeron?"

Hacer predicciones

Genera predicciones para nuevos escenarios:

# Create new data for prediction
new_data <- data.frame(
  day_of_week = factor("Fri", levels = levels(data$day_of_week)),
  marketing_spend = 300,
  temperature = 25
)

# Predict expected counts
predicted_counts <- predict(model, newdata = new_data, type = "response")
print(paste("Expected visitors:", round(predicted_counts, 1)))

[1] "Expected visitors: 45.2"

El modelo predice 45,2 visitantes para un viernes con un gasto en marketing de 300 $ y una temperatura de 25°C. Esta predicción entra dentro del rango razonable de nuestros datos observados (39-58 visitantes) y se aproxima a nuestra media general de 46,9 visitantes.

La regresión de Poisson garantiza de forma natural que las predicciones sigan siendo números enteros positivos cuando se redondean, a diferencia de la regresión lineal, que podría producir valores negativos imposibles. El parámetro type = "response" devuelve predicciones en la escala de recuento original, en lugar de la escala logarítmica utilizada internamente por el modelo.

Diagnóstico esencial del modelo

Comprobación de la sobredispersión

La sobredispersión se produce cuando la varianza supera a la media, violando un supuesto clave de Poisson:

# Calculate dispersion statistic
residual_deviance <- model$deviance
df_residual <- model$df.residual
dispersion <- residual_deviance / df_residual

print(paste("Dispersion statistic:", round(dispersion, 3)))

if (dispersion > 1.5) {
  print("Possible overdispersion detected")
  print("Consider quasi-Poisson or negative binomial models")
}

[1] "Dispersion statistic: 0.849"

El estadístico de dispersión de 0,849 se aproxima a 1, lo que indica que nuestro modelo se ajusta bien a los datos sin una dispersión excesiva significativa. Los valores próximos a 1 sugieren que la hipótesis de Poisson de igual media y varianza es razonable para este conjunto de datos.

Como el estadístico es inferior a 1,5, no aparece ningún mensaje de advertencia, lo que confirma que la regresión de Poisson estándar es adecuada. Si este valor fuera mucho mayor que 1 (normalmente por encima de 1,5), tendríamos que considerar modelos cuasi-Poisson o binomiales negativos para tener en cuenta la variabilidad extra.

Análisis residual

Examina los residuos para detectar patrones o violaciones del modelo:

# Calculate Pearson residuals
fitted_values <- fitted(model)
pearson_residuals <- residuals(model, type = "pearson")

# Plot residuals vs fitted values
plot(fitted_values, pearson_residuals,
     xlab = "Fitted Values", ylab = "Pearson Residuals",
     main = "Residuals vs Fitted")
abline(h = 0, col = "red", lty = 2)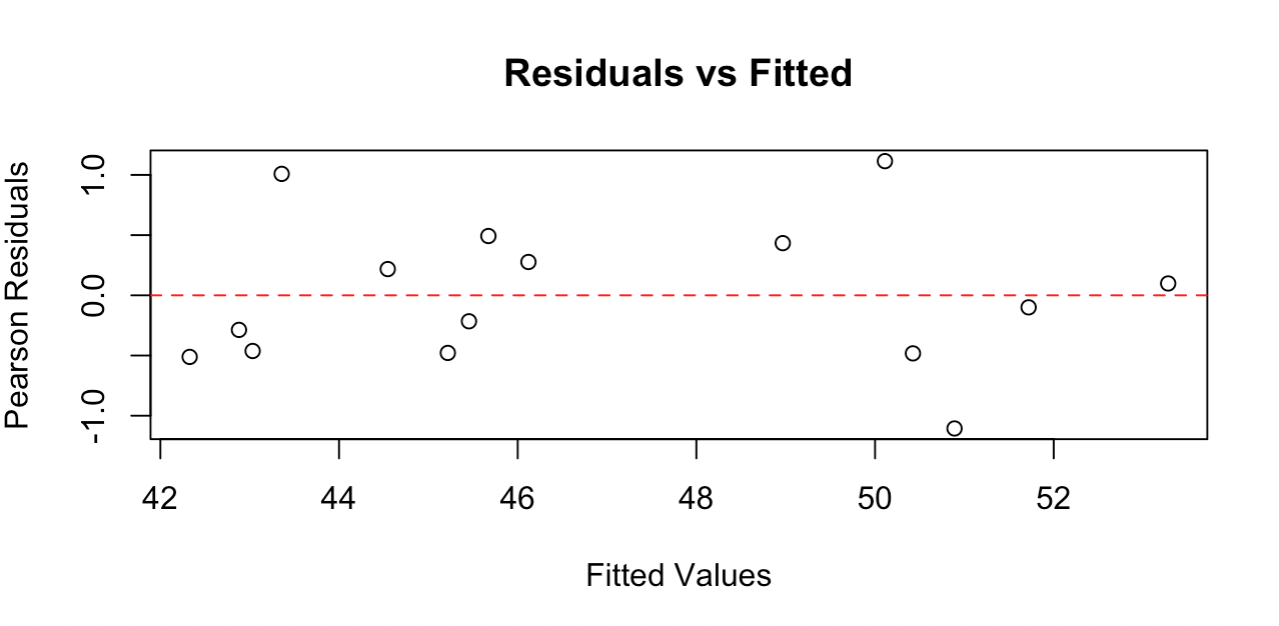

Gráfico de residuos que muestra una dispersión aleatoria en torno a cero. Imagen del autor.

El gráfico de residuos muestra puntos dispersos aleatoriamente alrededor de la línea cero sin patrones claros, lo que indica que nuestro modelo se ajusta bien a los datos. Los residuos oscilan aproximadamente entre -1 y +1, lo que es razonable para este tamaño de muestra.

Los buenos gráficos de residuos deben mostrar: dispersión aleatoria en torno a cero (sin patrones curvos), dispersión aproximadamente constante entre los valores ajustados (sin formas de embudo) y sin valores extremos atípicos. Este gráfico cumple todos estos criterios, lo que confirma que se cumplen los supuestos de la regresión de Poisson y que nuestro modelo proporciona resultados fiables.

Tratamiento de la dispersión excesiva

Si se detecta sobredispersión, considera modelos cuasi-Poisson que ajusten los errores estándar:

# Fit quasi-Poisson model
quasi_model <- glm(visitors ~ day_of_week + marketing_spend + temperature, 
                   family = quasipoisson, data = data)

Como nuestro modelo muestra una buena dispersión (0,849), aquí no se necesitan ajustes cuasi-Poisson. Sin embargo, este enfoque proporciona intervalos de confianza y valores p más conservadores cuando la varianza supera a la media, lo que lo convierte en una herramienta valiosa para los datos de recuento del mundo real que a menudo presentan sobredispersión.

Presentar e interpretar los resultados

Crear resúmenes de resultados claros

Transforma los resultados del modelo en conocimientos relevantes para la empresa centrándote en el significado práctico de tus TIR. Cuando tu modelo muestre que los días de fin de semana tienen una TIR de 1,4 en comparación con los días entre semana, comunícalo como "los fines de semana tienen un 40% más de visitantes que los días entre semana". Cuando el gasto en marketing tiene una TIR de 1,002, explica que "cada dólar adicional en marketing se asocia con un aumento aproximado del 0,2% en visitantes".

Para las variables continuas, considera la posibilidad de presentar los efectos a intervalos significativos. En lugar de discutir el efecto de un cambio de temperatura de un solo grado, muestra el impacto de una diferencia de 10 grados, que podría ser más relevante para la planificación empresarial.

Comprender las limitaciones del modelo

La regresión de Poisson identifica asociaciones, no relaciones causales. Una fuerte asociación entre el gasto en marketing y el número de visitantes no prueba que el marketing cause el aumento.  Otros factores podrían influir en ambas variables. Reconoce esta limitación al presentar los resultados.

El modelo supone que la tasa permanece constante para unos valores predictores dados. Si tu empresa tiene tendencias estacionales no recogidas por tus variables, o si la relación entre predictores y resultados cambia con el tiempo, tu modelo podría no generalizarse bien a periodos futuros.

Retos comunes y soluciones

Tratamiento de los recuentos cero

Los datos de recuento suelen contener ceros, que son perfectamente válidos en la regresión de Poisson. Sin embargo, si tus datos tienen muchos más ceros de lo que predeciría una distribución de Poisson, esto podría indicar un proceso de generación de datos diferente. Algunas observaciones podrían representar periodos o condiciones en los que el acontecimiento simplemente no puede ocurrir, en lugar de periodos en los que podría ocurrir pero no ocurrió.

Por ejemplo, el recuento de visitantes de un sitio web puede incluir ceros para los días en que el sitio estuvo inactivo por mantenimiento. Estos "ceros estructurales" son distintos de los "ceros aleatorios" que se dan de forma natural en los procesos de Poisson.

Estrategia de construcción de modelos

Empieza con tus predictores más importantes basados en el conocimiento del dominio. Añade variables de una en una y evalúa si mejoran tu comprensión de los datos. Los modelos más complejos no siempre son mejores.

Presta atención a la importancia práctica de los efectos, no sólo a la importancia estadística. Un cambio estadísticamente significativo del 1% en los índices de sucesos podría no justificar una acción empresarial, mientras que un cambio del 20% que no sea significativo en absoluto podría justificar una investigación con más datos.

Tratamiento de las infracciones

Cuando falla la equidispersión (varianza mucho mayor que la media), la regresión cuasi-Poisson proporciona una solución sencilla. Mantiene la misma estructura del modelo, pero ajusta los errores estándar para tener en cuenta la variabilidad adicional. Esto produce intervalos de confianza y valores p más conservadores.

Para la sobredispersión grave, la regresión binomial negativa modela explícitamente la variación extra. Este enfoque estima tanto la relación media como la variabilidad adicional.

Buenas prácticas y recomendaciones

Evitar errores comunes

No ignores la sobredispersión: es una de las violaciones más comunes de los supuestos de Poisson y puede afectar gravemente a tus conclusiones. Comprueba siempre la relación entre la varianza y la media y considera alternativas cuando sea necesario.

Ten cuidado con extrapolar más allá de tu rango de datos. Si tus datos de gasto en marketing oscilan entre 100 y 1000 $, no predigas con confianza efectos para niveles de gasto de 5000 $. La relación puede no seguir siendo log-lineal en los valores extremos.

Evita tratar todos los predictores categóricos como si tuvieran el mismo espaciado entre niveles. Las categorías de educación (bachillerato, algunos estudios universitarios, graduado universitario) pueden no tener los mismos efectos en tu variable de resultado.

Documentación y flujo de trabajo

Documenta tus decisiones de modelado, especialmente las violaciones de supuestos y cómo las abordaste. Si descubriste sobredispersión pero elegiste ajustes cuasi-Poisson, ten en cuenta esta decisión y sus implicaciones para la interpretación.

Conclusión

La regresión de Poisson proporciona un marco eficaz para analizar datos de recuento en muchos ámbitos. Cuando apliques estas técnicas a tus propios datos, empieza con modelos sencillos y aumenta gradualmente la complejidad basándote tanto en pruebas estadísticas como en la experiencia en el campo. Cuando se incumplen los supuestos, extensiones como los modelos cuasi-Poisson o binomial negativo ofrecen buenas alternativas. El objetivo no es sólo la significación estadística, sino una visión práctica que permita tomar mejores decisiones.

Si quieres profundizar en tus conocimientos sobre regresión, nuestro curso Regresión Intermedia en R abarca técnicas avanzadas de diagnóstico y estrategias de modelado que complementan los conocimientos sobre regresión de Poisson que has aprendido aquí. Los Modelos Lineales Generalizados en R son otra gran opción.