Regressão de Poisson: Uma maneira de modelar dados de contagem

Ao analisar dados que envolvem a contagem de eventos, como o número de reclamações de clientes por dia, internações hospitalares por mês ou cliques em sites por hora, a regressão linear comum geralmente produz resultados enganosos. Os dados de contagem têm características exclusivas que exigem abordagens de modelagem especializadas.

A regressão de Poisson fornece um método estatístico projetado especificamente para dados de contagem. Diferentemente da regressão linear, que pode prever valores negativos, a regressão de Poisson garante que as previsões permaneçam como números inteiros não negativos. Isso o torna particularmente valioso em qualquer campo em que a contagem de eventos seja fundamental para a tomada de decisões.

Se você não tem experiência em análise de regressão, nosso curso Introduction to Regression in R fornece os conceitos básicos essenciais de que você precisará para este tutorial. Para aqueles que estão prontos para explorar a família mais ampla de técnicas de regressão, o Generalized Linear Models in R oferece uma cobertura abrangente da estrutura estatística que inclui a regressão de Poisson.

Compreensão dos dados de contagem e seus desafios

O que torna os dados de contagem especiais

Os dados de contagem representam o número de vezes que algo acontece em um período ou espaço fixo. Os exemplos incluem o número de reclamações de seguro registradas por apólice por ano ou o número de acidentes de trânsito em um cruzamento por mês.

Os dados de contagem têm várias propriedades distintas que tornam a regressão linear comum inadequada:

• Somente números inteiros não negativos: As contagens não podem ser negativas ou fracionárias. 
• Distribuição assimétrica direita: A maioria dos conjuntos de dados de contagem mostra muitos valores baixos com valores altos ocasionais, criando uma cauda direita característica.
• A variância aumenta com a média: À medida que as contagens médias aumentam, a variabilidade normalmente também aumenta. 

Por que a regressão linear falha

Considere a possibilidade de prever o número de reclamações de clientes com base em fatores como a complexidade do produto e as pontuações de satisfação do cliente. A regressão linear trata isso como qualquer resultado contínuo, prevendo potencialmente valores impossíveis como -1,5 reclamações ou 14,7 reclamações.

De forma mais problemática, a regressão linear pressupõe uma variação constante em todos os níveis de previsão. Na realidade, as semanas com contagens de reclamações previstas mais altas provavelmente mostrarão mais variabilidade do que as semanas com contagens previstas baixas. Esse padrãon, chamado de heterocedasticidade, leva a intervalos de confiança e testes de hipóteses não confiáveis.

A base da distribuição de Poisson

A regressão de Poisson se baseia na distribuição de probabilidade de Poisson, que descreve naturalmente os dados de contagem. A distribuição de Poisson tem um único parâmetro (lambda) que representa a média e a variância das contagens. Essa propriedade de média-variância igual, chamada de equidispersão, é uma suposição fundamental que precisaremos verificar na prática.

A distribuição é excelente na modelagem de eventos "raros" - não necessariamente infrequentes, mas eventos em que cada ocorrência individual é independente e a taxa permanece relativamente constante em condições semelhantes.

Quando usar a regressão de Poisson

Primeiro, vamos falar sobre as condições ideais sob as quais a regressão de Poisson tem um bom desempenho. Depois, podemos falar sobre os aplicativos reais. 

Cenários ideais

A regressão de Poisson funciona melhor quando seus dados atendem a várias condições:

• Eventos independentes: Cada ocorrência não influencia as outras. Um sinistro de seguro não torna outro mais ou menos provável (supondo que não haja padrões de fraude).
• Taxa constante: Em condições semelhantes, a taxa média de eventos permanece estável. As visitas ao pronto-socorro podem variar de acordo com o dia da semana, mas as terças-feiras em meses semelhantes devem apresentar padrões consistentes.
• Quadro de tempo ou espaço adequado: Os eventos são contados em períodos ou áreas claramente definidos. "Reclamações por mês" é melhor do que "reclamações às vezes contadas diariamente, às vezes semanalmente".
• Não há excesso de zeros evidentes: Embora alguns zeros sejam esperados, se os seus dados tiverem muito mais zeros do que a distribuição de Poisson prevê, você pode precisar de modelos especializados inflados com zero.

Aplicativos comuns

Na área de saúde e epidemiologia, os pesquisadores rastreiam casos de doenças em regiões ou períodos de tempo, ajustando-os à população. Por exemplo, eles podem estudar como as taxas de vacinação influenciam as infecções por 100.000 pessoas.

Nos negócios e no marketing, as equipes examinam o comportamento do cliente, como frequência de compras, tíquetes de suporte ou envolvimento. As empresas de comércio eletrônico geralmente modelam os pedidos diários com base em gastos com marketing, sazonalidade e promoções.

Ou aqui está um exemplo comum frequentemente mencionado com a regressão de Poisson: As equipes de produção monitoram as taxas de defeitos por tamanho de lote ou período de inspeção para detectar problemas de qualidade antecipadamente e melhorar os processos.

Entendendo a estrutura e as suposições do modelo

A conexão do link de registro

A regressão de Poisson não modela contagens diretamente. Em vez disso, ele modela o logaritmo da contagem esperada como uma combinação linear de preditores.

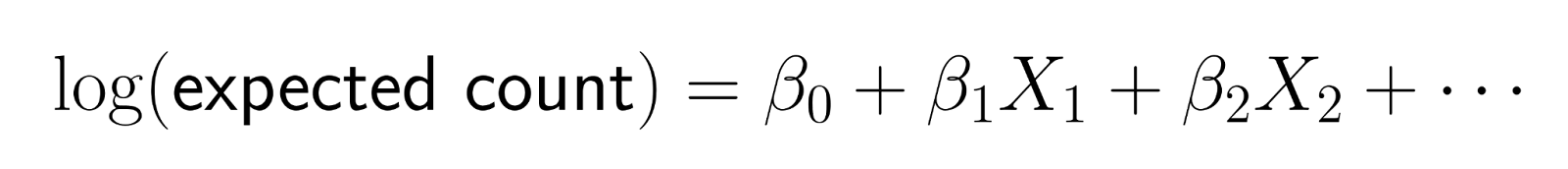
Essa transformação logarítmica garante que as previsões permaneçam positivas. Especificamente, a função log-link transforma a contagem esperada para a escala logarítmica, garantindo que as previsões do modelo para a contagemmédia de permaneçam estritamente positivas. Quando invertemos a transformação (exponenciando), obtemos:

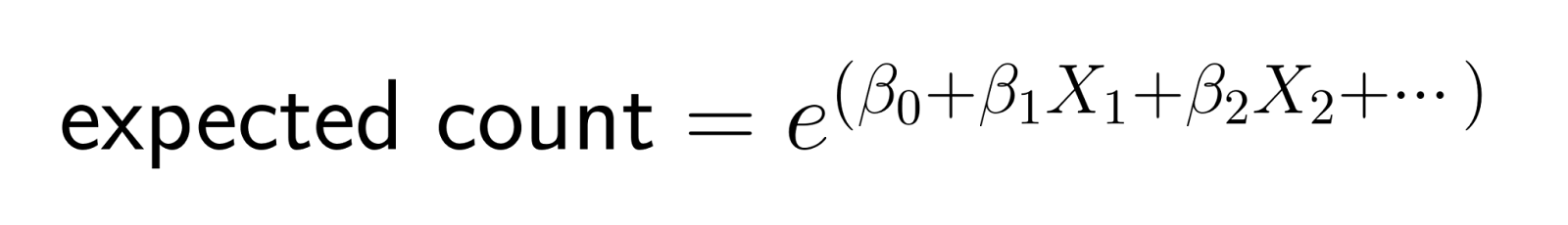
Essa estrutura significa que as alterações nos preditores têm efeitos multiplicativos na contagem esperada. 

Interpretação de efeitos multiplicativos

Na regressão linear, o aumento de uma unidade em um preditor adiciona uma quantidade constante ao resultado. Na regressão de Poisson, o aumento de um preditor em uma unidade multiplica a contagem esperada por um fator constante.

Por exemplo, se o coeficiente para "gastos com marketing" for 0,1, então cada dólar adicional de gastos com marketing multiplica o número esperado de clientes por e^0,1 ≈ 1,105, representando um aumento de cerca de 10,5%.

Embora pareça mais complicada, essa característica pode ser intuitiva para aplicativos comerciais, nos quais geralmente pensamos em termos de alterações percentuais e efeitos relativos.

Principais suposições a serem verificadas

Como em qualquer modelo, há algumas suposições às quais precisamos prestar atenção: 

• Independência: As observações não devem influenciar umas às outras. Se você estiver analisando contagens diárias ao longo do tempo, padrões temporais fortes podem indicar dependência que exige uma modelagem mais sofisticada.
• Equidispersão: A variação deve ser aproximadamente igual à média. Calcule essa proporção para seus dados - valores muito maiores que 1 sugerem dispersão excessiva que precisa ser tratada.
• Forma funcional correta: A relação entre os preditores e a contagem de registros deve ser aproximadamente linear. As relações não lineares podem exigir termos polinomiais ou transformações.
• Não há discrepâncias graves: Valores extremos de contagem podem influenciar desproporcionalmente os resultados. Investigue se os valores discrepantes representam erros de dados ou eventos extremos genuínos.

Trabalhando com exposição e compensações

Compreensão das variáveis de exposição

Muitos conjuntos de dados de contagem envolvem diferentes níveis de exposição - períodos de tempo variáveis, tamanhos de população ou intensidades de observação. Por exemplo, para comparar a contagem de acidentes entre cidades, é necessário levar em conta as diferenças populacionais, ou para comparar os números de vendas mensais, é necessário observar que alguns meses têm números diferentes de dias.

As variáveis de exposição representam o "denominador" que torna as contagens comparáveis. Sem o ajuste adequado, cidades maiores terão trivialmente mais acidentes e meses mais longos terão vendas mais altas, mascarando potencialmente as verdadeiras relações que você deseja estudar.

Implementação de compensações

As compensações oferecem uma maneira de incorporar variáveis de exposição com um coeficiente fixado em 1. Em vez de modelar contagens brutas, os offsets permitem que você modele taxas enquanto mantém a estrutura de contagem dos dados.

A forma matemática é a seguinte:

Rearranjando essa equação:

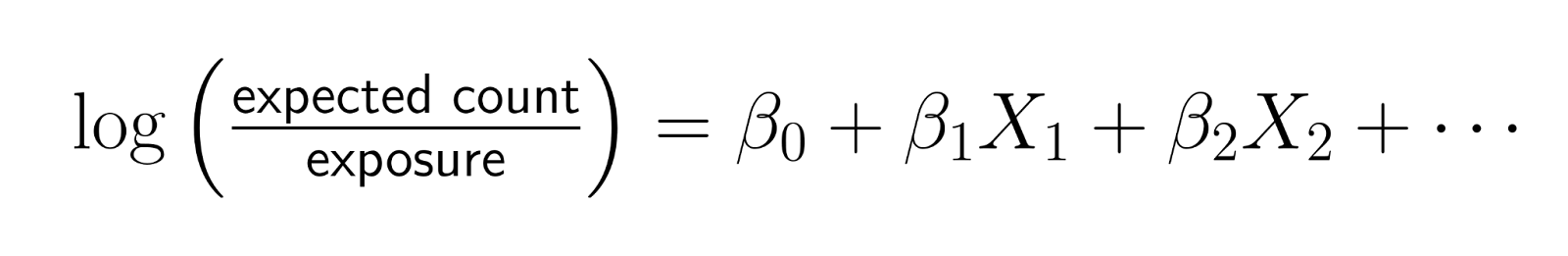
Isso mostra que você está modelando efetivamente a taxa logarítmica, em que taxa = contagem/exposição.

Quando esse pensamento é útil

• Taxas de doença ajustadas à população: Ao comparar as contagens de casos de COVID-19 entre os condados, inclua log(população) como uma compensação. Dessa forma, os coeficientes representam efeitos sobre casos por pessoa em vez de casos totais.
• Métricas de negócios ajustadas ao tempo: Se você estiver analisando vendas mensais com alguns meses com períodos promocionais diferentes, inclua log(promotional_days) como uma compensação para estudar as vendas por dia promocional.
• Dados ambientais ajustados por área: Ao contar as observações de espécies em diferentes áreas de habitat, inclua log(area_surveyed) como uma compensação para modelar a densidade de espécies em vez de contagens brutas.

O deslocamento garante que a duplicação da exposição duplique a contagem esperada (tudo o mais constante), que é a relação natural para fenômenos baseados em taxas.

Interpretação de coeficientes e resultados

De coeficientes a taxas de incidência

Os coeficientes de regressão de Poisson brutos representam mudanças na contagem de logs, o que pode ser difícil de interpretar diretamente. A exponenciação dos coeficientes os transforma em taxas de incidência (IRRs), que têm interpretações intuitivas.

Uma IRR representa a mudança multiplicativa na contagem esperada para um aumento de uma unidade no preditor:

• IRR = 1.0: Sem efeito (o preditor não altera a taxa)
• IRR = 1.2: Aumento de 20% na taxa
• IRR = 0.8: Redução de 20% na taxa
• IRR = 2.0: Aumento de 100% (dobrando a taxa)

Interpretação de diferentes tipos de preditores

• Preditores contínuos: Se a idade tiver uma TIR de 1,03, cada ano adicional de idade multiplica a contagem esperada por 1,03, representando um aumento de 3%. Para uma diferença de idade de 10 anos, o efeito seria de 1,03^10 ≈ 1,34, ou cerca de um aumento de 34%.
• Preditores binários: Se o gênero (masculino vs. feminino) tiver uma TIR de 1,5, os homens têm 1,5 vezes a taxa do resultado em comparação com as mulheres, o que representa uma taxa 50% maior.
• Preditores categóricos: Com várias categorias, cada nível é comparado a uma categoria de referência. Se o "inverno" tiver uma IRR de 0,7 em comparação com o "verão", os meses de inverno apresentam 30% menos eventos do que os meses de verão.

Compreensão dos intervalos de confiança

Os intervalos de confiança da TIR fornecem estimativas de incerteza em torno de suas taxas. Uma TIR de 1,25 com um intervalo de confiança de 95% de [1,10, 1,42] sugere que você pode estar razoavelmente confiante de que o efeito real representa um aumento entre 10% e 42% na taxa.

Se um intervalo de confiança incluir 1,0, o efeito pode não ser estatisticamente significativo. Por exemplo, uma IRR de 1,15 com IC [0,95, 1,39] sugere que o preditor pode não ter efeito.

Estratégias práticas de comunicação

Ao apresentar os resultados para públicos não técnicos, concentre-se em alterações percentuais em vez de proporções. Em vez de dizer "a TIR é 1,3", diga "esse fator está associado a um aumento de 30% na taxa de eventos".

Forneça exemplos concretos: "Com base em nosso modelo, o aumento dos gastos com marketing em US$ 1.000 está associado a aproximadamente 15% mais aquisições de clientes, de uma média de 20 para cerca de 23 clientes por mês."

Implementação da regressão de Poisson no R

Agora que já analisamos os detalhes da interpretação, vamos implementar no R.

Preparação e exploração de dados

Antes de ajustar qualquer modelo, examine cuidadosamente seus dados de contagem. Comece carregando as bibliotecas necessárias e explorando a distribuição:

library(ggplot2)
library(dplyr)

# Example: Website daily visitor counts
data <- data.frame(
  visitors = c(42, 48, 39, 52, 44, 58, 51, 47, 41, 49, 40, 46, 43, 54, 50),
  day_of_week = factor(c("Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun",
                        "Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun", "Mon")),
  marketing_spend = c(200, 150, 180, 250, 220, 400, 350, 300, 160, 190,
                     140, 210, 380, 420, 170),
  temperature = c(22, 25, 19, 24, 26, 28, 30, 27, 21, 23, 18, 25, 29, 31, 20)
)

# Check mean vs variance (should be similar for Poisson)
mean(data$visitors)
var(data$visitors)
var(data$visitors) / mean(data$visitors) # Should be close to 1

# Visualize the distribution
ggplot(data, aes(x = visitors)) +
  geom_histogram(bins = 8, fill = "lightblue", color = "black") +
  labs(title = "Distribution of Daily Visitors",
       x = "Number of Visitors", y = "Frequency")

> mean(data$visitors)
[1] 46.93333
> var(data$visitors)
[1] 30.35238
> var(data$visitors) / mean(data$visitors)
[1] 0.6467127

A relação entre a variância e a média de 0,65 é razoavelmente próxima de 1, indicando que nossos dados são adequados para a regressão de Poisson. Embora não sejam exatamente iguais, as proporções entre 0,5 e 1,5 são geralmente aceitáveis e sugerem que a distribuição de Poisson oferece uma boa base para modelar esses dados de contagem.

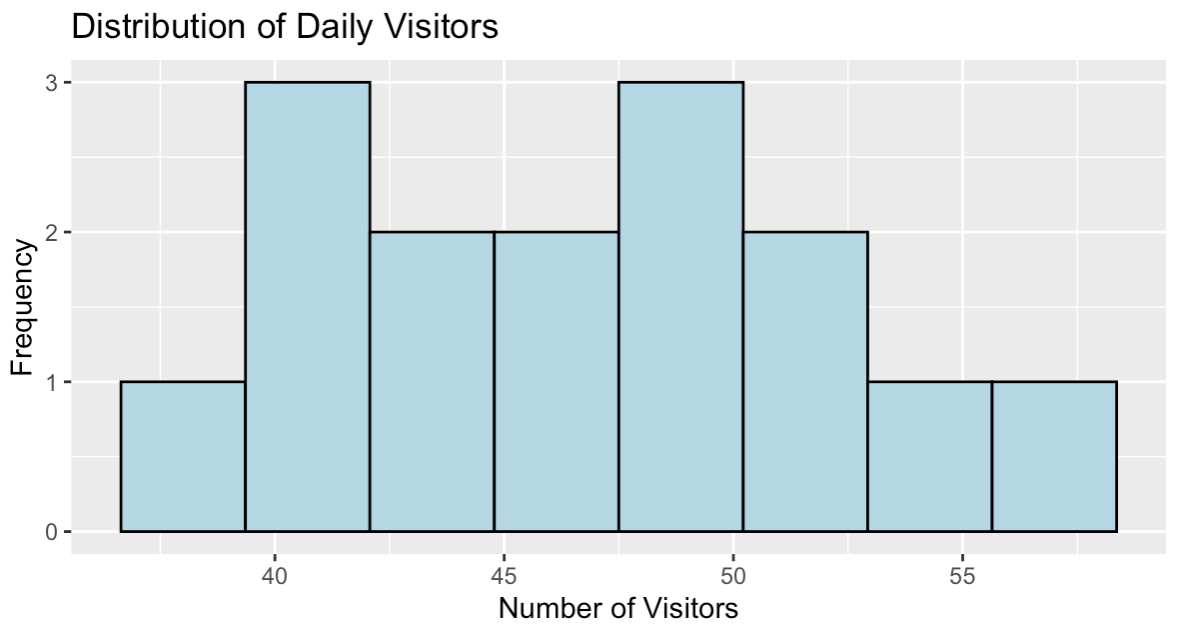
Distribuição dos visitantes diários do site. Imagem do autor.

O histograma mostra uma distribuição aproximadamente simétrica de contagens de visitantes centrada em torno de 47 visitantes por dia, com valores que variam de 39 a 58. Esse padrão de distribuição é consistente com os dados de contagem que podem ser modelados com eficiência usando a regressão de Poisson.

Ajuste do modelo

A função glm() com family = poisson ajusta os modelos de regressão de Poisson:

# Basic Poisson regression
model <- glm(visitors ~ day_of_week + marketing_spend + temperature,
             family = poisson, data = data)

# View key model results
summary(model)

# Calculate Incidence Rate Ratios (IRRs)
exp(coefficients(model))

Aqui você encontra a tabela de coeficientes:

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)    
(Intercept)     3.2978122  0.5556601   5.935 2.94e-09 ***
day_of_weekMon  0.0724036  0.1635467   0.443    0.658    
day_of_weekSat  0.0316265  0.2872878   0.110    0.912    
day_of_weekSun  0.0339621  0.2502578   0.136    0.892    
day_of_weekThu  0.1068756  0.1870821   0.571    0.568    
day_of_weekTue  0.0442967  0.1633032   0.271    0.786    
day_of_weekWed  0.0653789  0.1813230   0.361    0.718    
marketing_spend 0.0001593  0.0018211   0.087    0.930    
temperature     0.0186099  0.0317682   0.586    0.558

Aqui estão as taxas de incidência (IRRs):

(Intercept)  day_of_weekMon  day_of_weekSat  day_of_weekSun  day_of_weekThu  day_of_weekTue  day_of_weekWed marketing_spend 
27.053386        1.075089        1.032132        1.034545        1.112796        1.045292        1.067563        1.000159 
temperature 
1.018784 

Os coeficientes mostram os efeitos da escala logarítmica, mas as IRRs fornecem interpretações mais intuitivas. Por exemplo, quinta-feira (day_of_weekThu) tem uma TIR de 1,11, sugerindo cerca de 11% mais visitantes em comparação com sexta-feira (a categoria de referência). Os gastos com marketing têm uma TIR de 1,0002, indicando que cada dólar adicional aumenta os visitantes esperados em cerca de 0,02%.

Observe que, se calculássemos os intervalos de confiança para essas IRRs, muitos incluiriam 1,0, sugerindo que os efeitos não são estatisticamente significativos com essa pequena amostra. Isso é comum em conjuntos de dados pequenos e demonstra por que o tamanho da amostra é importante.

Inclusão de exposição com compensações

Se seus dados tiverem períodos de exposição variáveis, inclua-os como compensações:

# Example with exposure data
data$exposure_days <- c(rep(7, 10), rep(6, 5))  # Some weeks had 6 observation days

# Model with offset
model_offset <- glm(visitors ~ day_of_week + marketing_spend + temperature + 
                   offset(log(exposure_days)), 
                   family = poisson, data = data)

summary(model_offset)

Call:
glm(formula = visitors ~ day_of_week + marketing_spend + temperature + 
    offset(log(exposure_days)), family = poisson, data = data)

Coefficients:
                  Estimate Std. Error z value Pr(>|z|)   
(Intercept)      1.734e+00  5.579e-01   3.109  0.00188 **
day_of_weekMon   2.371e-02  1.637e-01   0.145  0.88485   
day_of_weekSat   9.873e-02  2.898e-01   0.341  0.73338   
day_of_weekSun   1.208e-01  2.472e-01   0.489  0.62513   
day_of_weekThu   5.642e-02  1.871e-01   0.302  0.76297   
day_of_weekTue  -6.713e-02  1.634e-01  -0.411  0.68128   
day_of_weekWed  -6.073e-02  1.825e-01  -0.333  0.73934   
marketing_spend -4.231e-05  1.823e-03  -0.023  0.98149   
temperature      8.210e-03  3.179e-02   0.258  0.79623

Observe como os coeficientes mudam drasticamente quando incluímos o deslocamento. O intercepto cai de 3,30 para 1,73, e todos os outros efeitos se tornam menores. Essa transformação ocorre porque agora estamos modelando a taxa por dia em vez de contagens totais em períodos variáveis.

A compensação garante comparações justas, ajustando para diferentes comprimentos de exposição. Sem esse ajuste, os períodos com mais dias de observação pareceriam artificialmente ter contagens mais altas de visitantes, o que poderia mascarar as verdadeiras relações que queremos estudar. O modelo agora responde "Qual é a taxa de visitantes diários?" em vez de "Quantos visitantes totais ocorreram?".

Fazendo previsões

Gerar previsões para novos cenários:

# Create new data for prediction
new_data <- data.frame(
  day_of_week = factor("Fri", levels = levels(data$day_of_week)),
  marketing_spend = 300,
  temperature = 25
)

# Predict expected counts
predicted_counts <- predict(model, newdata = new_data, type = "response")
print(paste("Expected visitors:", round(predicted_counts, 1)))

[1] "Expected visitors: 45.2"

O modelo prevê 45,2 visitantes para uma sexta-feira com gastos de marketing de US$ 300 e temperatura de 25°C. Essa previsão está dentro da faixa razoável de nossos dados observados (39-58 visitantes) e está próxima de nossa média geral de 46,9 visitantes.

A regressão de Poisson garante naturalmente que as previsões permaneçam números inteiros positivos quando arredondadas, ao contrário da regressão linear, que poderia produzir valores negativos impossíveis. O parâmetro type = "response" retorna as previsões na escala de contagem original em vez da escala de log usada internamente pelo modelo.

Diagnóstico de modelos essenciais

Verificação de dispersão excessiva

A superdispersão ocorre quando a variação excede a média, violando uma suposição fundamental de Poisson:

# Calculate dispersion statistic
residual_deviance <- model$deviance
df_residual <- model$df.residual
dispersion <- residual_deviance / df_residual

print(paste("Dispersion statistic:", round(dispersion, 3)))

if (dispersion > 1.5) {
  print("Possible overdispersion detected")
  print("Consider quasi-Poisson or negative binomial models")
}

[1] "Dispersion statistic: 0.849"

A estatística de dispersão de 0,849 está próxima de 1, indicando que nosso modelo se ajusta bem aos dados sem dispersão excessiva significativa. Valores próximos a 1 sugerem que a suposição de Poisson de média e variância iguais é razoável para esse conjunto de dados.

Como a estatística está abaixo de 1,5, nenhuma mensagem de aviso é exibida, confirmando que a regressão de Poisson padrão é adequada. Se esse valor fosse muito maior que 1 (normalmente acima de 1,5), precisaríamos considerar modelos quase-Poisson ou binomiais negativos para levar em conta a variabilidade extra.

Análise residual

Examine os resíduos para detectar padrões ou violações do modelo:

# Calculate Pearson residuals
fitted_values <- fitted(model)
pearson_residuals <- residuals(model, type = "pearson")

# Plot residuals vs fitted values
plot(fitted_values, pearson_residuals,
     xlab = "Fitted Values", ylab = "Pearson Residuals",
     main = "Residuals vs Fitted")
abline(h = 0, col = "red", lty = 2)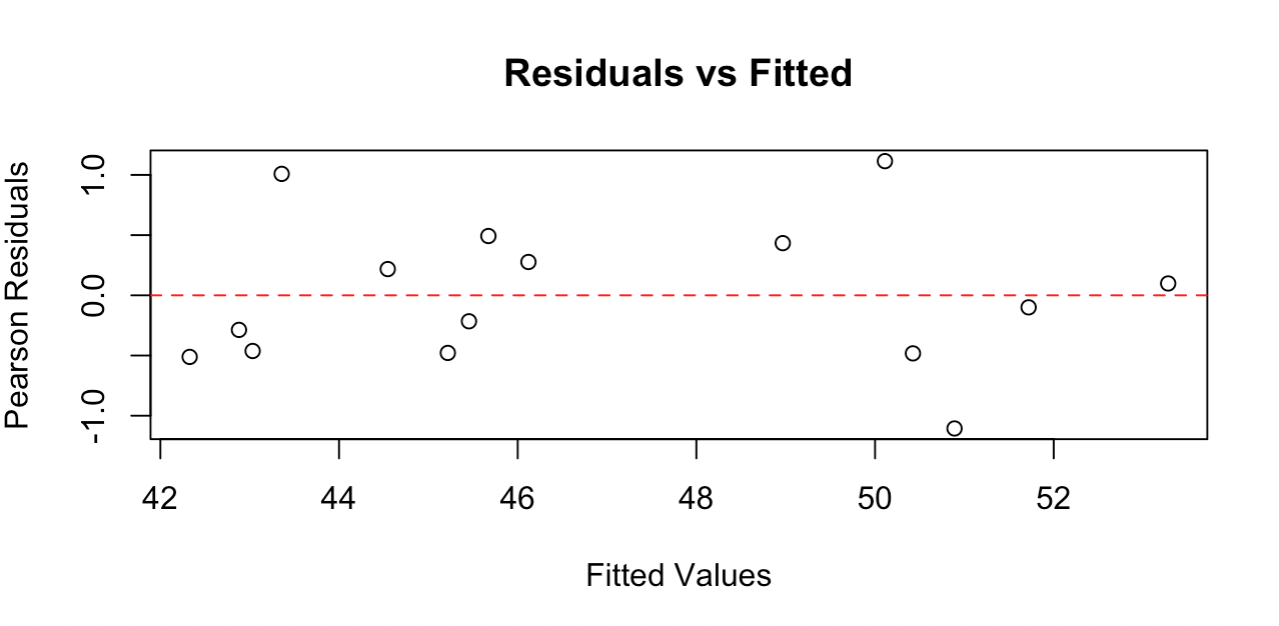

Gráfico residual mostrando dispersão aleatória em torno de zero. Imagem do autor.

O gráfico residual mostra pontos espalhados aleatoriamente em torno da linha zero, sem padrões claros, indicando que nosso modelo se ajusta bem aos dados. Os resíduos variam aproximadamente de -1 a +1, o que é razoável para esse tamanho de amostra.

Bons gráficos residuais devem mostrar: dispersão aleatória em torno de zero (sem padrões curvos), dispersão aproximadamente constante entre os valores ajustados (sem formas de funil) e sem valores extremos discrepantes. Esse gráfico atende a todos esses critérios, confirmando que as suposições da regressão de Poisson são satisfeitas e que nosso modelo fornece resultados confiáveis.

Como lidar com a dispersão excessiva

Se for detectada dispersão excessiva, considere modelos quase Poisson que ajustem os erros padrão:

# Fit quasi-Poisson model
quasi_model <- glm(visitors ~ day_of_week + marketing_spend + temperature, 
                   family = quasipoisson, data = data)

Como nosso modelo mostra uma boa dispersão (0,849), os ajustes de quase-Poisson não são necessários aqui. No entanto, essa abordagem fornece intervalos de confiança e valores de p mais conservadores quando a variação excede a média, o que a torna uma ferramenta valiosa para dados de contagem do mundo real que frequentemente apresentam dispersão excessiva.

Apresentação e interpretação de resultados

Criar resumos claros dos resultados

Transforme o resultado do modelo em insights relevantes para os negócios, concentrando-se no significado prático de suas TIRs. Quando seu modelo mostrar que os dias de fim de semana têm uma TIR de 1,4 em comparação com os dias de semana, comunique isso como "os fins de semana recebem cerca de 40% mais visitantes do que os dias de semana". Quando os gastos com marketing tiverem uma TIR de 1,002, explique que "cada dólar adicional em marketing está associado a um aumento de cerca de 0,2% nos visitantes".

Para variáveis contínuas, considere apresentar os efeitos em intervalos significativos. Em vez de discutir o efeito de uma mudança de temperatura de um grau, mostre o impacto de uma diferença de 10 graus, que pode ser mais relevante para o planejamento de negócios.

Compreensão das limitações do modelo

A regressão de Poisson identifica associações, não relações causais. Uma forte associação entre os gastos com marketing e o número de visitantes não prova que o marketing causa o aumento.  Outros fatores podem influenciar ambas as variáveis. Reconheça essa limitação ao apresentar os resultados.

O modelo pressupõe que a taxa permanece constante para determinados valores de previsão. Se sua empresa tiver tendências sazonais não capturadas por suas variáveis ou se a relação entre preditores e resultados mudar com o tempo, seu modelo poderá não ser bem generalizado para períodos futuros.

Desafios e soluções comuns

Lidando com contagens zero

Os dados de contagem geralmente contêm zeros, que são perfeitamente válidos na regressão de Poisson. No entanto, se os seus dados tiverem muito mais zeros do que uma distribuição de Poisson poderia prever, isso pode indicar um processo diferente de geração de dados. Algumas observações podem representar períodos ou condições em que o evento simplesmente não pode ocorrer, em vez de períodos em que ele poderia ocorrer, mas não ocorreu.

Por exemplo, a contagem de visitantes do site pode incluir zeros para os dias em que o site ficou fora do ar para manutenção. Esses "zeros estruturais" são diferentes dos "zeros aleatórios" que ocorrem naturalmente nos processos de Poisson.

Estratégia de construção de modelos

Comece com seus preditores mais importantes com base no conhecimento do domínio. Adicione variáveis uma de cada vez e avalie se elas melhoram sua compreensão dos dados. Modelos mais complexos nem sempre são melhores.

Preste atenção à importância prática dos efeitos, não apenas à importância estatística. Uma mudança estatisticamente significativa de 1% nas taxas de eventos pode não justificar uma ação comercial, enquanto uma mudança de 20% que é marginalmente não significativa ainda pode justificar uma investigação com mais dados.

Tratamento de violações

Quando a equidispersão falha (variância muito maior que a média), a regressão quase-Poisson oferece uma solução simples. Ele mantém a mesma estrutura de modelo, mas ajusta os erros padrão para levar em conta a variabilidade extra. Isso produz intervalos de confiança e valores p mais conservadores.

Para dispersão excessiva grave, a regressão binomial negativa modela explicitamente a variação extra. Essa abordagem estima tanto a relação média quanto a variabilidade adicional.

Práticas recomendadas e recomendações

Como evitar erros comuns

Não ignore a dispersão excessiva - essa é uma das violações mais comuns das suposições de Poisson e pode afetar gravemente suas conclusões. Sempre verifique a relação entre a variância e a média e considere alternativas quando necessário.

Seja cauteloso ao extrapolar além do intervalo de dados. Se seus dados de gastos com marketing variam de US$ 100 a US$ 1.000, não preveja com confiança os efeitos para níveis de gastos de US$ 5.000. A relação pode não permanecer log-linear em valores extremos.

Evite tratar todos os preditores categóricos como tendo o mesmo espaçamento entre os níveis. As categorias de educação (ensino médio, alguma faculdade, pós-graduação) podem não ter efeitos iguais na variável de resultado.

Documentação e fluxo de trabalho

Documente suas decisões de modelagem, especialmente as violações de suposições e como você as abordou. Se você descobriu a superdispersão, mas optou por ajustes quase Poisson, observe essa decisão e suas implicações para a interpretação.

Conclusão

A regressão de Poisson oferece uma estrutura eficaz para analisar dados de contagem em muitos domínios. À medida que você aplicar essas técnicas aos seus próprios dados, comece com modelos simples e aumente a complexidade gradualmente com base em evidências estatísticas e conhecimento do domínio. Quando as pressuposições são violadas, extensões como modelos quase-Poisson ou binomiais negativos oferecem boas alternativas. O objetivo não é apenas a significância estatística, mas insights práticos que informam melhores decisões.

Se você deseja aprofundar sua experiência em regressão, nosso curso Intermediate Regression in R abrange técnicas avançadas de diagnóstico e estratégias de modelagem que complementam as habilidades de regressão de Poisson que você aprendeu aqui. Modelos lineares generalizados no R são outra ótima opção.