Poisson-Regression: Ein Weg zur Modellierung von Zähldaten

Bei der Analyse von Daten, die das Zählen von Ereignissen beinhalten - wie die Anzahl der Kundenbeschwerden pro Tag, der Krankenhauseinweisungen pro Monat oder der Website-Klicks pro Stunde - führt die gewöhnliche lineare Regression oft zu irreführenden Ergebnissen. Zähldaten haben einzigartige Eigenschaften, die spezielle Modellierungsansätze erfordern.

Die Poisson-Regression ist eine statistische Methode, die speziell für Zähldaten entwickelt wurde. Im Gegensatz zur linearen Regression, die negative Werte vorhersagen kann, stellt die Poisson-Regression sicher, dass die Vorhersagen nicht-negative ganze Zahlen bleiben. Das macht sie besonders wertvoll für alle Bereiche, in denen das Zählen von Ereignissen eine zentrale Rolle bei der Entscheidungsfindung spielt.

Wenn du neu in der Regressionsanalyse bist, vermittelt dir unser Kurs Einführung in die Regression in R die grundlegenden Konzepte, die du für dieses Tutorial brauchst. Für diejenigen, die bereit sind, die breitere Familie der Regressionsverfahren zu erkunden, bietet Generalized Linear Models in R eine umfassende Abdeckung des statistischen Rahmens, der auch die Poisson-Regression umfasst.

Zähldaten und ihre Herausforderungen verstehen

Was macht Zähldaten so besonders?

Zähldaten geben an, wie oft etwas in einem bestimmten Zeitraum oder Raum passiert. Beispiele dafür sind die Anzahl der Versicherungsfälle pro Police und Jahr oder die Anzahl der Verkehrsunfälle an einer Kreuzung pro Monat.

Zähldaten haben mehrere besondere Eigenschaften, die eine gewöhnliche lineare Regression ungeeignet machen:

• Nur nichtnegative ganze Zahlen: Zählungen können nicht negativ oder gebrochen sein. 
• Rechtsschiefe Verteilung: Die meisten Zähldatensätze weisen viele niedrige Werte mit gelegentlich hohen Werten auf, wodurch ein charakteristischer rechter Schwanz entsteht.
• Die Varianz steigt mit dem Mittelwert: Je höher die durchschnittliche Anzahl ist, desto größer ist in der Regel auch die Variabilität. 

Warum die lineare Regression versagt

Erwäge, die Anzahl der Kundenbeschwerden anhand von Faktoren wie Produktkomplexität und Kundenzufriedenheit vorherzusagen. Die lineare Regression behandelt dies wie jedes andere kontinuierliche Ergebnis und sagt möglicherweise unmögliche Werte wie -1,5 Beschwerden oder 14,7 Beschwerden voraus.

Noch problematischer ist, dass die lineare Regression von einer konstanten Varianz über alle Vorhersageebenen hinweg ausgeht. In der Realität werden Wochen mit höheren prognostizierten Beschwerdezahlen wahrscheinlich eine größere Variabilität aufweisen als Wochen mit niedrigen prognostizierten Zahlen. Dieses Mustern, Heteroskedastizität genannt, führt zu unzuverlässigen Konfidenzintervallen und Hypothesentests.

Die Grundlage der Poisson-Verteilung

Die Poisson-Regression basiert auf der Poisson-Wahrscheinlichkeitsverteilung, die natürlich Zähldaten beschreibt. Die Poisson-Verteilung hat einen einzigen Parameter (lambda), der sowohl den Mittelwert als auch die Varianz der Zählungen darstellt. Diese Eigenschaft der gleichen mittleren Varianz, auch Äquidispersion genannt, ist eine der wichtigsten Annahmen, die wir in der Praxis überprüfen müssen.

Die Verteilung eignet sich hervorragend zur Modellierung "seltener" Ereignisse - nicht unbedingt selten, aber Ereignisse, bei denen jedes einzelne Auftreten unabhängig ist und die Rate unter ähnlichen Bedingungen relativ konstant bleibt.

Wann wird die Poisson-Regression verwendet?

Lass uns zunächst über die idealen Bedingungen sprechen, unter denen die Poisson-Regression gut funktioniert. Dann können wir über die tatsächlichen Anwendungen sprechen. 

Ideale Szenarien

Die Poisson-Regression funktioniert am besten, wenn deine Daten mehrere Bedingungen erfüllen:

• Unabhängige Veranstaltungen: Jedes Ereignis hat keinen Einfluss auf andere. Ein Versicherungsfall macht einen anderen nicht wahrscheinlicher oder unwahrscheinlicher (vorausgesetzt, es gibt keine Betrugsmuster).
• Konstante Rate: Unter ähnlichen Bedingungen bleibt die durchschnittliche Rate der Ereignisse stabil. Die Besuche in der Notaufnahme können von Wochentag zu Wochentag variieren, aber Dienstage in ähnlichen Monaten sollten einheitliche Muster aufweisen.
• Richtiger Zeit- oder Raumrahmen: Die Ereignisse werden über klar definierte Zeiträume oder Bereiche gezählt. "Beschwerden pro Monat" ist besser als "Beschwerden werden manchmal täglich, manchmal wöchentlich gezählt".
• Keine offensichtlichen überzähligen Nullen: Einige Nullen sind zwar zu erwarten, aber wenn deine Daten viel mehr Nullen aufweisen, als die Poisson-Verteilung vorhersagen würde, brauchst du möglicherweise spezielle Modelle mit Nullen.

Gemeinsame Anwendungen

Im Gesundheitswesen und in der Epidemiologie verfolgen Forscher die Krankheitsfälle über Regionen oder Zeiträume hinweg und berücksichtigen dabei die Bevölkerungszahl. Sie können zum Beispiel untersuchen, wie die Impfquoten die Infektionen pro 100.000 Menschen beeinflussen.

In der Wirtschaft und im Marketing untersuchen die Teams das Kundenverhalten wie Kaufhäufigkeit, Support-Tickets oder Engagement. E-Commerce-Unternehmen modellieren die täglichen Bestellungen oft auf der Grundlage von Marketingausgaben, Saisonalität und Werbeaktionen.

Oder hier ist ein gängiges Beispiel, das oft im Zusammenhang mit der Poisson-Regression genannt wird: Fertigungsteams überwachen die Fehlerraten nach Losgröße oder Prüfzeitraum, um Qualitätsprobleme frühzeitig zu erkennen und Prozesse zu verbessern.

Verstehen der Modellstruktur und Annahmen

Die Log-Link-Verbindung

Die Poisson-Regression modelliert die Zählungen nicht direkt. Stattdessen wird der Logarithmus der erwarteten Anzahl als lineare Kombination von Prädiktoren modelliert.

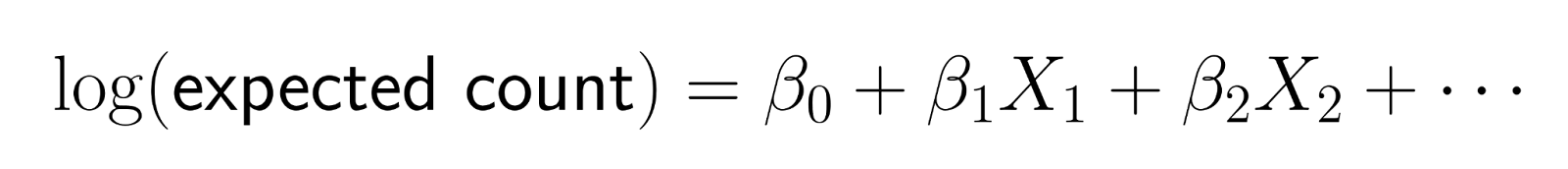
Diese logarithmische Umwandlung sorgt dafür, dass die Vorhersagen positiv bleiben. Die Log-Link-Funktion wandelt die erwartete Anzahl in die logarithmische Skala um und stellt so sicher, dass die Modellvorhersagen für die mittlere Anzahl streng positiv bleiben. Wenn wir die Transformation umkehren (indem wir potenzieren), erhalten wir:

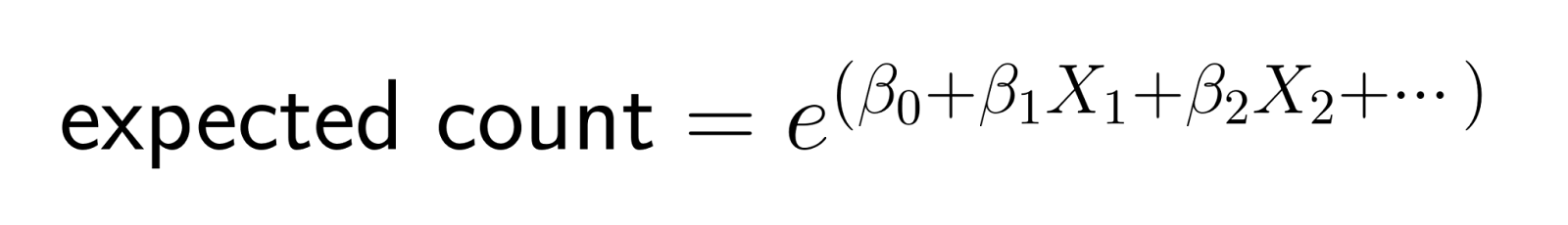
Diese Struktur bedeutet, dass Änderungen der Prädiktoren multiplikative Auswirkungen auf die erwartete Anzahl haben. 

Multiplikationseffekte interpretieren

Bei der linearen Regression erhöht die Erhöhung eines Prädiktors um eine Einheit das Ergebnis um einen konstanten Betrag. Bei der Poisson-Regression multipliziert die Erhöhung eines Prädiktors um eine Einheit die erwartete Anzahl um einen konstanten Faktor.

Wenn der Koeffizient für "Marketingausgaben" zum Beispiel 0,1 beträgt, dann multipliziert jeder zusätzliche Dollar an Marketingausgaben die erwartete Anzahl der Kunden mit e^0,1 ≈ 1,105, was einer Steigerung von etwa 10,5 % entspricht.

Auch wenn es komplizierter erscheint, kann diese Eigenschaft für Geschäftsanwendungen intuitiv sein, wo wir oft in Form von prozentualen Veränderungen und relativen Auswirkungen denken.

Zu überprüfende Schlüsselannahmen

Wie bei jedem Modell gibt es einige Annahmen, auf die wir achten müssen: 

• Unabhängigkeit: Die Beobachtungen sollten sich nicht gegenseitig beeinflussen. Wenn du tägliche Zählungen im Laufe der Zeit analysierst, können starke zeitliche Muster auf eine Abhängigkeit hinweisen, die eine anspruchsvollere Modellierung erfordert.
• Äquidispersion: Die Varianz sollte ungefähr dem Mittelwert entsprechen. Berechne dieses Verhältnis für deine Daten - Werte, die viel größer als 1 sind, deuten auf eine übermäßige Streuung hin, die behandelt werden muss.
• Korrekte Funktionsform: Die Beziehung zwischen Prädiktoren und Log-Zahl sollte ungefähr linear sein. Nicht lineare Beziehungen können polynomische Terme oder Umformungen erfordern.
• Keine schweren Ausreißer: Extreme Zählwerte können die Ergebnisse unverhältnismäßig stark beeinflussen. Untersuche, ob Ausreißer Datenfehler oder echte Extremereignisse darstellen.

Arbeiten mit Belichtung und Offsets

Die Variablen der Exposition verstehen

Viele Zähldatensätze beinhalten verschiedene Expositionsniveaus - unterschiedliche Zeiträume, Bevölkerungsgrößen oder Beobachtungsintensitäten. Wenn du z. B. die Zahl der Unfälle in verschiedenen Städten vergleichst, musst du die unterschiedlichen Bevölkerungszahlen berücksichtigen, oder wenn du monatliche Umsatzzahlen vergleichst, musst du beachten, dass manche Monate eine unterschiedliche Anzahl von Tagen haben.

Expositionsvariablen sind der "Nenner", der die Zählungen vergleichbar macht. Ohne die richtige Anpassung haben größere Städte trivialerweise mehr Unfälle und längere Monate höhere Umsätze, wodurch die wahren Zusammenhänge, die du untersuchen willst, möglicherweise verdeckt werden.

Umsetzung von Kompensationen

Offsets bieten eine Möglichkeit, Expositionsvariablen mit einem festen Koeffizienten von 1 einzubeziehen. Anstatt rohe Zählungen zu modellieren, kannst du mit Offsets Raten modellieren und dabei die Zählstruktur deiner Daten beibehalten.

Die mathematische Form lautet:

Wenn du diese Gleichung umstellst:

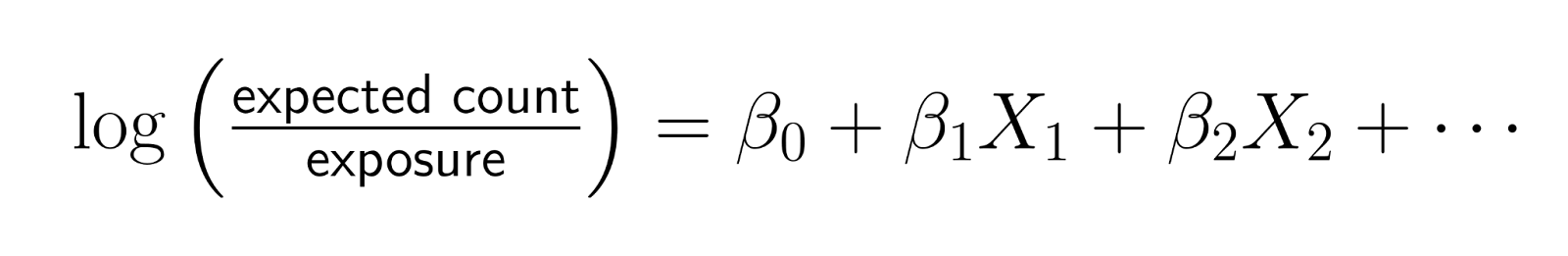
Das zeigt, dass du effektiv die log-Rate modellierst, wobei Rate = Anzahl/Exposition ist.

Wann dieses Denken nützlich ist

• Bevölkerungsbereinigte Krankheitsraten: Wenn du die COVID-19-Fallzahlen zwischen den Bezirken vergleichst, schließe log(Bevölkerung) als Offset ein. Auf diese Weise stellen die Koeffizienten die Auswirkungen auf die Fälle pro Person und nicht auf die Gesamtfälle dar.
• Zeitbereinigte Geschäftskennzahlen: Wenn du monatliche Umsätze analysierst und einige Monate unterschiedliche Aktionszeiträume haben, füge log(Aktionstage) als Offset hinzu, um die Umsätze pro Aktionstag zu untersuchen.
• Flächenbereinigte Umweltdaten: Bei der Zählung von Arten, die in verschiedenen Lebensraumgebieten gesichtet wurden, solltest du log(area_surveyed) als Offset einbeziehen, um die Artendichte zu modellieren, anstatt nur die Anzahl der Arten zu zählen.

Der Offset stellt sicher, dass eine Verdopplung der Exposition die erwartete Anzahl verdoppelt (unter sonst gleichen Bedingungen), was die natürliche Beziehung für ratenbasierte Phänomene ist.

Interpretation der Koeffizienten und Ergebnisse

Von Koeffizienten zu Inzidenzratenverhältnissen

Rohe Poisson-Regressionskoeffizienten stellen Veränderungen in der Log-Zahl dar, die schwer direkt zu interpretieren sein können. Durch die Potenzierung der Koeffizienten werden diese in Inzidenzraten (IRR) umgewandelt, die intuitiv zu interpretieren sind.

Eine IRR stellt die multiplikative Veränderung der erwarteten Anzahl für eine Erhöhung des Prädiktors um eine Einheit dar:

• IRR = 1.0: Keine Auswirkung (der Prädiktor verändert die Rate nicht)
• IRR = 1.2: Erhöhung des Satzes um 20%
• IRR = 0.8: Senkung des Satzes um 20%
• IRR = 2.0: 100%ige Erhöhung (Verdoppelung des Satzes)

Interpretation verschiedener Prädikatorentypen

• Kontinuierliche Prädiktoren: Wenn das Alter einen IRR von 1,03 hat, multipliziert jedes zusätzliche Jahr des Alters die erwartete Anzahl mit 1,03, was einem Anstieg von 3 % entspricht. Bei einem Altersunterschied von 10 Jahren würde der Effekt 1,03^10 ≈ 1,34 betragen, also etwa 34 % mehr.
• Binäre Prädiktoren: Wenn das Geschlecht (männlich vs. weiblich) eine IRR von 1,5 hat, haben Männer im Vergleich zu Frauen eine 1,5-mal höhere Rate des Ergebnisses, also eine 50% höhere Rate.
• Kategoriale Prädiktoren: Bei mehreren Kategorien wird jede Stufe mit einer Referenzkategorie verglichen. Wenn der "Winter" eine IRR von 0,7 im Vergleich zum "Sommer" hat, gibt es in den Wintermonaten 30% weniger Ereignisse als in den Sommermonaten.

Konfidenzintervalle verstehen

IRR-Konfidenzintervalle liefern Unsicherheitsschätzungen rund um deine Ratenkennzahlen. Ein IRR von 1,25 mit einem 95 %-Konfidenzintervall von [1,10, 1,42] lässt darauf schließen, dass der wahre Effekt zwischen 10 % und 42 % liegt.

Wenn ein Konfidenzintervall 1,0 umfasst, ist der Effekt möglicherweise statistisch nicht signifikant. Ein IRR von 1,15 mit CI [0,95, 1,39] deutet zum Beispiel darauf hin, dass der Prädiktor keine Wirkung hat.

Praktische Kommunikationsstrategien

Wenn du deine Ergebnisse einem nicht-technischen Publikum präsentierst, solltest du dich auf prozentuale Veränderungen konzentrieren und nicht auf Verhältniszahlen. Anstatt zu sagen: "Der IRR beträgt 1,3", sagst du: "Dieser Faktor ist mit einem Anstieg der Ereignisrate um 30 % verbunden."

Nenne konkrete Beispiele: "Unser Modell zeigt, dass eine Erhöhung der Marketingausgaben um 1.000 US-Dollar mit einer Steigerung der Kundenakquise um etwa 15 % verbunden ist, von durchschnittlich 20 auf etwa 23 Kunden pro Monat."

Implementierung der Poisson-Regression in R

Nachdem wir uns nun die Details der Interpretation angesehen haben, können wir sie in R implementieren.

Datenaufbereitung und -exploration

Bevor du ein Modell anpasst, solltest du deine Zähldaten genau untersuchen. Beginne damit, die notwendigen Bibliotheken zu laden und die Distribution zu erkunden:

library(ggplot2)
library(dplyr)

# Example: Website daily visitor counts
data <- data.frame(
  visitors = c(42, 48, 39, 52, 44, 58, 51, 47, 41, 49, 40, 46, 43, 54, 50),
  day_of_week = factor(c("Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun",
                        "Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun", "Mon")),
  marketing_spend = c(200, 150, 180, 250, 220, 400, 350, 300, 160, 190,
                     140, 210, 380, 420, 170),
  temperature = c(22, 25, 19, 24, 26, 28, 30, 27, 21, 23, 18, 25, 29, 31, 20)
)

# Check mean vs variance (should be similar for Poisson)
mean(data$visitors)
var(data$visitors)
var(data$visitors) / mean(data$visitors) # Should be close to 1

# Visualize the distribution
ggplot(data, aes(x = visitors)) +
  geom_histogram(bins = 8, fill = "lightblue", color = "black") +
  labs(title = "Distribution of Daily Visitors",
       x = "Number of Visitors", y = "Frequency")

> mean(data$visitors)
[1] 46.93333
> var(data$visitors)
[1] 30.35238
> var(data$visitors) / mean(data$visitors)
[1] 0.6467127

Das Verhältnis von Varianz zu Mittelwert liegt mit 0,65 ziemlich nahe bei 1, was darauf hindeutet, dass unsere Daten gut für eine Poisson-Regression geeignet sind. Obwohl sie nicht genau gleich sind, sind Verhältnisse zwischen 0,5 und 1,5 im Allgemeinen akzeptabel und legen nahe, dass die Poisson-Verteilung eine gute Grundlage für die Modellierung dieser Zähldaten bietet.

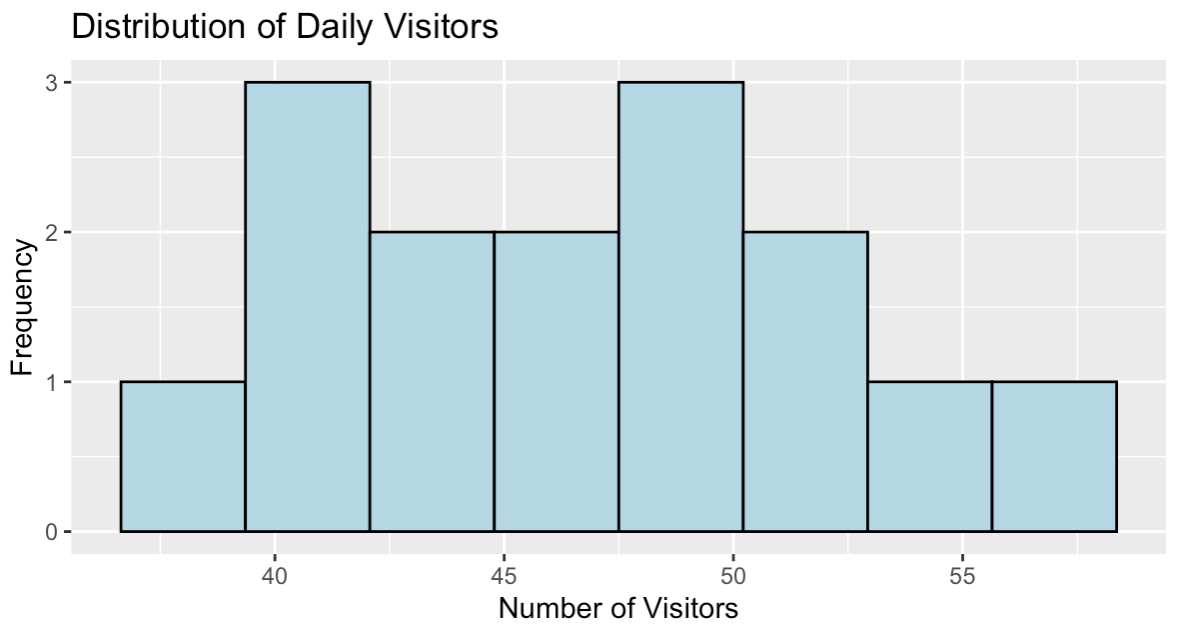
Verteilung der täglichen Website-Besucher. Bild vom Autor.

Das Histogramm zeigt eine annähernd symmetrische Verteilung der Besucherzahlen, die in der Mitte bei 47 Besuchern pro Tag liegt, wobei die Werte von 39 bis 58 reichen. Dieses Verteilungsmuster entspricht den Zähldaten, die mit der Poisson-Regression effektiv modelliert werden können.

Anpassen des Modells

Die Funktion glm() mit family = poisson passt Poisson-Regressionsmodelle an:

# Basic Poisson regression
model <- glm(visitors ~ day_of_week + marketing_spend + temperature,
             family = poisson, data = data)

# View key model results
summary(model)

# Calculate Incidence Rate Ratios (IRRs)
exp(coefficients(model))

Hier ist die Tabelle mit den Koeffizienten:

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)    
(Intercept)     3.2978122  0.5556601   5.935 2.94e-09 ***
day_of_weekMon  0.0724036  0.1635467   0.443    0.658    
day_of_weekSat  0.0316265  0.2872878   0.110    0.912    
day_of_weekSun  0.0339621  0.2502578   0.136    0.892    
day_of_weekThu  0.1068756  0.1870821   0.571    0.568    
day_of_weekTue  0.0442967  0.1633032   0.271    0.786    
day_of_weekWed  0.0653789  0.1813230   0.361    0.718    
marketing_spend 0.0001593  0.0018211   0.087    0.930    
temperature     0.0186099  0.0317682   0.586    0.558

Hier sind die Inzidenzratenquoten (IRRs):

(Intercept)  day_of_weekMon  day_of_weekSat  day_of_weekSun  day_of_weekThu  day_of_weekTue  day_of_weekWed marketing_spend 
27.053386        1.075089        1.032132        1.034545        1.112796        1.045292        1.067563        1.000159 
temperature 
1.018784 

Die Koeffizienten zeigen die logarithmischen Effekte, aber die IRRs bieten intuitivere Interpretationen. Der Donnerstag (day_of_weekThu) hat zum Beispiel eine IRR von 1,11, was bedeutet, dass er etwa 11% mehr Besucher hat als der Freitag (die Referenzkategorie). Marketingausgaben haben einen IRR von 1,0002, was bedeutet, dass jeder zusätzliche Dollar die erwarteten Besucher um etwa 0,02 % erhöht.

Wenn wir Konfidenzintervalle für diese IRRs berechnen würden, würden viele davon 1,0 enthalten, was darauf hindeutet, dass die Effekte bei dieser kleinen Stichprobe statistisch nicht signifikant sind. Das ist bei kleinen Datensätzen üblich und zeigt, warum die Stichprobengröße wichtig ist.

Einschließlich Exposition mit Offsets

Wenn deine Daten unterschiedliche Expositionszeiten haben, füge sie als Offsets hinzu:

# Example with exposure data
data$exposure_days <- c(rep(7, 10), rep(6, 5))  # Some weeks had 6 observation days

# Model with offset
model_offset <- glm(visitors ~ day_of_week + marketing_spend + temperature + 
                   offset(log(exposure_days)), 
                   family = poisson, data = data)

summary(model_offset)

Call:
glm(formula = visitors ~ day_of_week + marketing_spend + temperature + 
    offset(log(exposure_days)), family = poisson, data = data)

Coefficients:
                  Estimate Std. Error z value Pr(>|z|)   
(Intercept)      1.734e+00  5.579e-01   3.109  0.00188 **
day_of_weekMon   2.371e-02  1.637e-01   0.145  0.88485   
day_of_weekSat   9.873e-02  2.898e-01   0.341  0.73338   
day_of_weekSun   1.208e-01  2.472e-01   0.489  0.62513   
day_of_weekThu   5.642e-02  1.871e-01   0.302  0.76297   
day_of_weekTue  -6.713e-02  1.634e-01  -0.411  0.68128   
day_of_weekWed  -6.073e-02  1.825e-01  -0.333  0.73934   
marketing_spend -4.231e-05  1.823e-03  -0.023  0.98149   
temperature      8.210e-03  3.179e-02   0.258  0.79623

Beachte, wie sich die Koeffizienten dramatisch verändern, wenn wir den Offset einbeziehen. Der Achsenabschnitt sinkt von 3,30 auf 1,73, und alle anderen Effekte werden kleiner. Diese Umwandlung erfolgt, weil wir jetzt die Rate pro Tag modellieren und nicht mehr die Gesamtzahl über verschiedene Zeiträume.

Der Offset sorgt für faire Vergleiche, indem er unterschiedliche Belichtungszeiten ausgleicht. Ohne diese Anpassung würden Zeiträume mit mehr Beobachtungstagen künstlich den Anschein erwecken, höhere Besucherzahlen zu haben, was die wahren Beziehungen, die wir untersuchen wollen, verschleiern könnte. Das Modell antwortet nun auf die Frage "Wie hoch ist die tägliche Besucherzahl?" anstatt auf die Frage "Wie viele Besucher gab es insgesamt?"

Vorhersagen treffen

Erstelle Vorhersagen für neue Szenarien:

# Create new data for prediction
new_data <- data.frame(
  day_of_week = factor("Fri", levels = levels(data$day_of_week)),
  marketing_spend = 300,
  temperature = 25
)

# Predict expected counts
predicted_counts <- predict(model, newdata = new_data, type = "response")
print(paste("Expected visitors:", round(predicted_counts, 1)))

[1] "Expected visitors: 45.2"

Das Modell prognostiziert 45,2 Besucher für einen Freitag mit 300 $ Marketingausgaben und 25°C Temperatur. Diese Vorhersage liegt innerhalb des angemessenen Bereichs unserer beobachteten Daten (39-58 Besucher) und ist nahe an unserem Gesamtdurchschnitt von 46,9 Besuchern.

Die Poisson-Regression stellt natürlich sicher, dass die Vorhersagen beim Runden positive ganze Zahlen bleiben, im Gegensatz zur linearen Regression, die unmögliche negative Werte produzieren könnte. Der Parameter type = "response" liefert Vorhersagen auf der ursprünglichen Zählskala und nicht auf der vom Modell intern verwendeten logarithmischen Skala.

Wesentliche Modelldiagnosen

Überprüfung auf Überdispersion

Eine Überdispersion liegt vor, wenn die Varianz den Mittelwert übersteigt und damit eine wichtige Poisson-Annahme verletzt wird:

# Calculate dispersion statistic
residual_deviance <- model$deviance
df_residual <- model$df.residual
dispersion <- residual_deviance / df_residual

print(paste("Dispersion statistic:", round(dispersion, 3)))

if (dispersion > 1.5) {
  print("Possible overdispersion detected")
  print("Consider quasi-Poisson or negative binomial models")
}

[1] "Dispersion statistic: 0.849"

Die Dispersionsstatistik von 0,849 liegt nahe bei 1, was darauf hindeutet, dass unser Modell gut zu den Daten passt, ohne dass eine signifikante Überdispersion vorliegt. Werte nahe bei 1 deuten darauf hin, dass die Poisson-Annahme mit gleichem Mittelwert und gleicher Varianz für diesen Datensatz angemessen ist.

Da die Statistik unter 1,5 liegt, erscheint keine Warnmeldung, was bestätigt, dass die Standard-Poisson-Regression angemessen ist. Wäre dieser Wert viel größer als 1 (in der Regel über 1,5), müssten wir Quasi-Poisson- oder negative Binomialmodelle in Betracht ziehen, um die zusätzliche Variabilität zu berücksichtigen.

Residualanalyse

Untersuche die Residuen, um Muster oder Modellverstöße zu erkennen:

# Calculate Pearson residuals
fitted_values <- fitted(model)
pearson_residuals <- residuals(model, type = "pearson")

# Plot residuals vs fitted values
plot(fitted_values, pearson_residuals,
     xlab = "Fitted Values", ylab = "Pearson Residuals",
     main = "Residuals vs Fitted")
abline(h = 0, col = "red", lty = 2)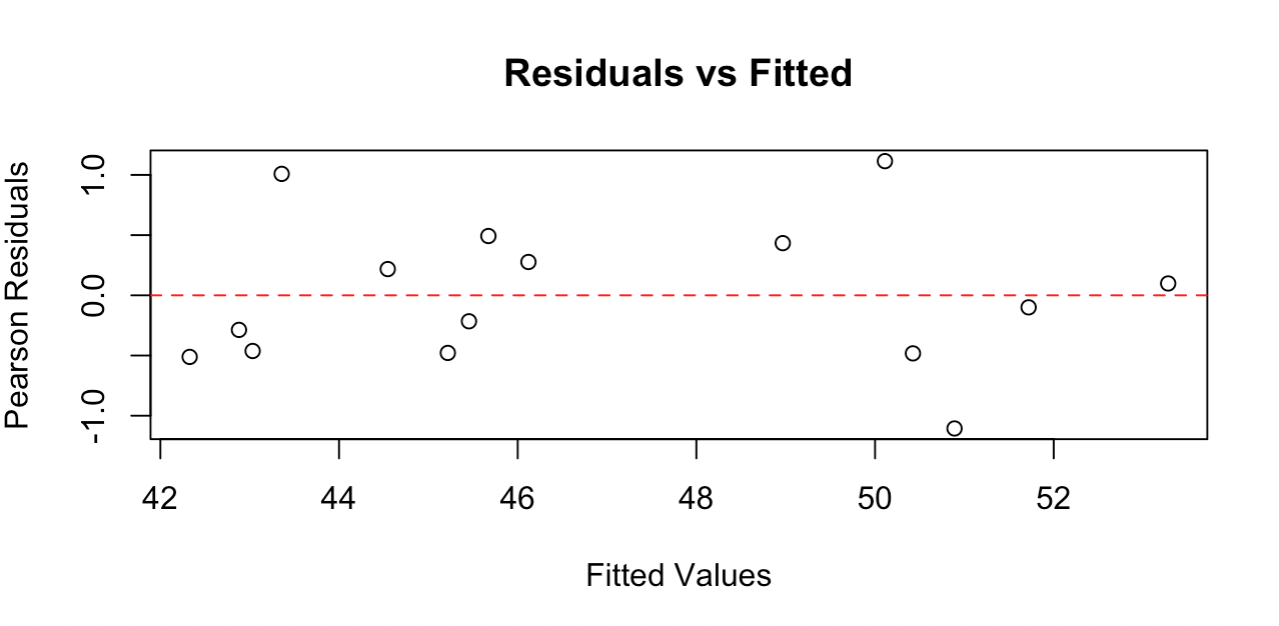

Das Residualdiagramm zeigt eine zufällige Streuung um den Nullpunkt. Bild vom Autor.

Das Residuen-Diagramm zeigt Punkte, die zufällig um die Nulllinie herum verstreut sind und kein klares Muster aufweisen, was zeigt, dass unser Modell gut zu den Daten passt. Die Residuen liegen ungefähr zwischen -1 und +1, was für diese Stichprobengröße angemessen ist.

Gute Residuen-Diagramme sollten Folgendes zeigen: eine zufällige Streuung um den Nullpunkt (keine gekrümmten Muster), eine ungefähr konstante Streuung der angepassten Werte (keine Trichterformen) und keine extremen Ausreißer. Diese Grafik erfüllt alle diese Kriterien und bestätigt, dass die Annahmen der Poisson-Regression erfüllt sind und unser Modell zuverlässige Ergebnisse liefert.

Umgang mit Überdispersion

Wenn eine Überdispersion festgestellt wird, solltest du Quasi-Poisson-Modelle in Betracht ziehen, die die Standardfehler anpassen:

# Fit quasi-Poisson model
quasi_model <- glm(visitors ~ day_of_week + marketing_spend + temperature, 
                   family = quasipoisson, data = data)

Da unser Modell eine gute Streuung aufweist (0,849), sind Quasi-Poisson-Anpassungen hier nicht erforderlich. Dieser Ansatz liefert jedoch konservativere Konfidenzintervalle und p-Werte, wenn die Varianz den Mittelwert übersteigt, was ihn zu einem wertvollen Instrument für reale Zähldaten macht, die oft eine Überdispersion aufweisen.

Ergebnisse präsentieren und interpretieren

Klare Ergebniszusammenfassungen erstellen

Verwandle die Modellergebnisse in geschäftsrelevante Erkenntnisse, indem du dich auf die praktische Bedeutung deiner IRRs konzentrierst. Wenn dein Modell zeigt, dass die Wochenendtage einen IRR von 1,4 im Vergleich zu den Wochentagen haben, kommuniziere dies als "An Wochenenden kommen etwa 40% mehr Besucher als an Wochentagen". Wenn Marketingausgaben einen IRR von 1,002 haben, erkläre, dass "jeder zusätzliche Dollar für Marketing mit einem Anstieg der Besucherzahlen um 0,2 % verbunden ist".

Bei kontinuierlichen Variablen solltest du die Effekte in sinnvollen Intervallen darstellen. Anstatt die Auswirkungen einer Temperaturveränderung von nur einem Grad zu erörtern, solltest du die Auswirkungen eines Unterschieds von 10 Grad aufzeigen, der für die Unternehmensplanung relevanter sein könnte.

Die Grenzen des Modells verstehen

Die Poisson-Regression identifiziert Assoziationen, nicht kausale Beziehungen. Ein starker Zusammenhang zwischen Marketingausgaben und Besucherzahlen beweist nicht, dass Marketing den Anstieg verursacht.  Andere Faktoren können beide Variablen beeinflussen. Bekenne dich zu dieser Einschränkung, wenn du deine Ergebnisse präsentierst.

Das Modell geht davon aus, dass die Rate bei gegebenen Prädikatorwerten konstant bleibt. Wenn es in deinem Unternehmen saisonale Trends gibt, die von deinen Variablen nicht erfasst werden, oder wenn sich die Beziehung zwischen Prädiktoren und Ergebnissen im Laufe der Zeit ändert, kann es sein, dass dein Modell nicht gut auf künftige Zeiträume verallgemeinert werden kann.

Gemeinsame Herausforderungen und Lösungen

Der Umgang mit Nullzählungen

Zähldaten enthalten oft Nullen, die in der Poisson-Regression durchaus zulässig sind. Wenn deine Daten jedoch viel mehr Nullen aufweisen, als eine Poisson-Verteilung vorhersagen würde, könnte dies auf einen anderen Prozess der Datengenerierung hindeuten. Einige Beobachtungen könnten Zeiträume oder Bedingungen darstellen, in denen das Ereignis einfach nicht eintreten kann, und nicht Zeiträume, in denen es eintreten könnte, aber nicht eingetreten ist.

Bei der Zählung von Website-Besuchern können zum Beispiel Nullen für Tage enthalten sein, an denen die Website wegen Wartungsarbeiten nicht erreichbar war. Diese "strukturellen Nullen" unterscheiden sich von "zufälligen Nullen", die bei Poisson-Prozessen natürlich vorkommen.

Strategie für den Modellbau

Beginne mit deinen wichtigsten Prädiktoren, die auf deinem Fachwissen basieren. Füge eine Variable nach der anderen hinzu und bewerte, ob sie dein Verständnis der Daten verbessert. Komplexere Modelle sind nicht immer besser.

Achte auf die praktische Bedeutung der Effekte, nicht nur auf die statistische Bedeutung. Eine statistisch signifikante Veränderung der Ereignisraten um 1 % rechtfertigt vielleicht keine geschäftlichen Maßnahmen, während eine Veränderung um 20 %, die nur geringfügig nicht signifikant ist, dennoch eine Untersuchung mit mehr Daten rechtfertigen kann.

Umgang mit Verstößen

Wenn die Äquidispersion versagt (Varianz viel größer als der Mittelwert), bietet die Quasi-Poisson-Regression eine einfache Lösung. Sie behält dieselbe Modellstruktur bei, passt aber die Standardfehler an, um die zusätzliche Variabilität zu berücksichtigen. Dies führt zu konservativeren Konfidenzintervallen und p-Werten.

Bei starker Überstreuung modelliert die negative Binomialregression explizit die zusätzliche Variation. Dieser Ansatz schätzt sowohl das mittlere Verhältnis als auch die zusätzliche Variabilität.

Bewährte Praktiken und Empfehlungen

Vermeiden von häufigen Fehlern

Ignoriere die Überdispersion nicht - sie ist eine der häufigsten Verletzungen der Poisson-Annahmen und kann deine Schlussfolgerungen stark beeinträchtigen. Überprüfe immer das Verhältnis von Varianz zu Mittelwert und ziehe bei Bedarf Alternativen in Betracht.

Sei vorsichtig mit Extrapolationen über deinen Datenbereich hinaus. Wenn die Daten zu deinen Marketingausgaben zwischen 100 und 1000 US-Dollar liegen, solltest du die Auswirkungen bei Ausgaben von 5000 US-Dollar nicht mit Sicherheit vorhersagen. Die Beziehung bleibt bei extremen Werten möglicherweise nicht log-linear.

Vermeide es, alle kategorialen Prädiktoren so zu behandeln, als hätten sie den gleichen Abstand zwischen den Stufen. Die Bildungskategorien (Highschool, etwas College, College-Absolvent) haben möglicherweise nicht die gleichen Auswirkungen auf deine Ergebnisvariable.

Dokumentation und Arbeitsablauf

Dokumentiere deine Modellierungsentscheidungen, insbesondere Verstöße gegen Annahmen und wie du sie behoben hast. Wenn du eine Überdispersion entdeckt hast, dich aber für Quasi-Poisson-Anpassungen entschieden hast, beachte diese Entscheidung und ihre Auswirkungen auf die Interpretation.

Fazit

Die Poisson-Regression bietet einen effektiven Rahmen für die Analyse von Zähldaten in vielen Bereichen. Wenn du diese Techniken auf deine eigenen Daten anwendest, beginne mit einfachen Modellen und steigere die Komplexität schrittweise auf der Grundlage von statistischen Erkenntnissen und Fachwissen. Wenn die Annahmen verletzt werden, bieten Erweiterungen wie Quasi-Poisson- oder negative Binomialmodelle gute Alternativen. Das Ziel ist nicht nur eine statistische Aussagekraft, sondern praktische Erkenntnisse, die zu besseren Entscheidungen führen.

Wenn du deine Regressionskenntnisse vertiefen möchtest, behandelt unser Kurs Intermediate Regression in R fortgeschrittene Diagnosetechniken und Modellierungsstrategien, die die hier erlernten Fähigkeiten zur Poisson-Regression ergänzen. Verallgemeinerte lineare Modelle in R sind eine weitere gute Option.