Précision et rappel : Le guide essentiel du machine learning

Un modèle d'apprentissage automatique avec une précision de 98 % semble remarquable, mais l'est-il réellement ? Lorsque vous êtes confronté à des événements rares tels que la fraude ou la maladie, la précision peut souvent créer un faux sentiment de sécurité.

C'est là que la précision et le rappel entrent en jeu. Dans cet article, nous examinerons comment ces deux indicateurs vont au-delà de la simple précision pour mesurer non seulement la fréquence à laquelle vous avez raison, mais aussi la manière dont vous vous trompez.

Si vous souhaitez aller au-delà de la théorie et maîtriser la classification, le cours « Détection des fraudes avec Python » est la prochaine étape idéale.

Pourquoi la précision n'est pas suffisante

Dans la plupart des cas, la précision est l'indicateur naturel utilisé pour mesurer la capacité d'un modèle statistique ou d'apprentissage automatique à prédire une certaine étiquette. Il est calculé en comparant le nombre d'instances correctement prédites au nombre total d'observations. 

De manière générale, si un modèle identifie systématiquement la bonne étiquette avec une grande précision, il fonctionne correctement. Cependant, les ensembles de données déséquilibrés, dans lesquels une classe contient beaucoup plus d'échantillons que l'autre, faussent la précision. De tels ensembles de données sont couramment utilisés dans la détection des fraudes ou le diagnostic des maladies.

Supposons qu'un modèle identifie les fraudes avec un taux de précision de 98 %. À première vue, ce taux semble remarquable. Cependant, que se passe-t-il si la fraude ne représente que 2 % des transactions dans l'ensemble de données ? Dans ce cas, un modèle pourrait choisir « pas de fraude » à chaque fois et obtenir tout de même un taux de précision de 98 % sans détecter aucune fraude, ce qui n'est pas le résultat souhaité. 

Il est évident que ce type de situation nécessite des indicateurs plus nuancés. Deux mesures couramment utilisées sontla précision et le rappelde l' . 

Que sont la précision et le rappel ?

Voici la version abrégée :

• Précision (qualité) : Mesure le degré de fiabilité de vos prévisions positives. Si le modèle indique « fraude », s'agit-il réellement d'une fraude ?
• Rappel (quantité) : Mesure dans quelle mesure vous avez correctement identifié les cas positifs réels. Le modèle a-t-il détecté toutes les fraudes ou certaines ont-elles échappé à la détection ?

Pour comprendre comment calculer ces indicateurs, il est toutefois nécessaire de définir au préalable la terminologie utilisée dans une matrice de confusion.

Véritable positif, faux positif et négatifs 

Prenons l'exemple d'une société émettrice de cartes de crédit qui utilise un modèle d'apprentissage automatique pour détecter les transactions frauduleuses par carte de crédit. Supposons que sur un échantillon de 10 000 transactions, 9 800 soient légitimes et 200 frauduleuses.

Pour mesurer l'efficacité du modèle, veuillez désigner l'un des cas comme « fraude » ou « non-fraude » comme cas positif et l'autre comme cas négatif. Étant donné que les cas de fraude présentent un intérêt particulier, veuillez les classer comme des cas « positifs ». (Cela ne signifie pas, bien entendu, que la fraude soit positive d'un point de vue éthique ; le terme « positif » désigne simplement le cas qui nous intéresse.)

Lorsque le modèle est exécuté, les transactions dont le score de risque dépasse un certain seuil de probabilité, par exemple 70 %, sont considérées comme frauduleuses. Les cas présumés frauduleux sont comparés à ceux qui le sont réellement.

Afin de clarifier toutes ces données, nous utilisons la nomenclature suivante. 

• Vrais positifs (TP) : 160 cas de fraude ont été correctement identifiés comme tels.
• Vrais négatifs (TN) : 9 500 cas ont été correctement identifiés comme n'étant pas frauduleux.
• Faux positifs (FP) : 300 cas ont été signalés à tort comme frauduleux.
• Faux négatifs (FN) : 40 cas ont été incorrectement classés comme non frauduleux.

La deuxième lettre (P ou N) indique si la prédiction était positive ou négative, et la première lettre indique si cette prédiction était vraie (V) ou fausse (F). 

Un « faux positif » indique que le système a prédit que le cas était positif, mais qu'il était en réalité négatif. Par exemple, un faux négatif est un cas qui a été prédit comme négatif, mais qui est en réalité positif.

Matrice de confusion

Toutes ces informations sont généralement présentées dans ce que l'on appelle la matrice de confusion, qui permet de suivre la fréquence à laquelle le modèle confond les prédictions incorrectes avec les résultats réels (FN, FP). La matrice de confusion nous aide à distinguer entre ce que le modèle a prédit et ce qui s'est réellement produit. La matrice de confusion de notre exemple se présente comme suit :his :

À présent,, examinons les totaux des lignes et des colonnes. Les sommes des lignes indiquent le nombre total de cas prévus, et les sommes des colonnes indiquent le nombre total de cas réels.

Que représentent ces totaux ?

• Le total de la première ligne (460) représente le nombre total de cas de fraude prédits (TP + FP).
• Le total de la deuxième ligne (9 540) représente le nombre total de cas légitimes prévus (FN + TN).
• Le total de la première colonne (200) représente le nombre total de cas de fraude avérés (TP + FN).
• Le total de la deuxième colonne (9 800) représente le nombre total de cas légitimes réels (FP + TN).
• Le total général (10 000) correspond à la taille totale de notre échantillon.

Qu'est-ce que la précision ?

L' e de précision mesure la qualité de vos prédictions positives. Il nous indique combien de cas prédits comme positifs étaient effectivement positifs. 

Un modèle précis implique un nombre très faible de fausses alertes. Si le modèle indique que quelque chose est vrai, il est fort probable que ce soit le cas. Par exemple, si un jeu en ligne exclut un joueur pour tricherie, cela doit être justifié. Un nombre excessif de bannissements injustifiés peut dissuader les utilisateurs légitimes et entraîner des évaluations négatives. 

Dans la terminologie examinée ci-dessus, la précision correspond au rapport entre les vrais positifs et les positifs prédits.

Dans l'exemple ci-dessus, la précision est de 160/460, soit environ 34,8 %.

Qu'est-ce que le rappel ?

Rappel: l' e mesure la couverture. Il nous montre combien de résultats positifs réels avaient été prédits comme tels. Il est défini comme le rapport entre les vrais positifs et le total des positifs réels.

Veuillez envisager les diagnostics de cancer pour le suivi initial. Est-il préférable de privilégier un diagnostic excessif ou un diagnostic insuffisant ? La plupart des personnes seraient d'accord avec la première affirmation. 

Dans le cadre d'un dépistage précoce, il peut être préoccupant de recevoir une fausse alerte. Cependant, il est extrêmement préoccupant d'apprendre que l'on n'a pas de cancer alors que c'est le cas, d'autant plus que cela pourrait entraîner le fait de ne pas bénéficier d'un traitement qui pourrait sauver la vie.

Dans l'exemple ci-dessus, le taux de rappel est de 160/200, soit 80 %.

Le compromis entre précision et rappel

Il existe une relation de tension entre la précision et le rappel. En général, lorsque la précision augmente, la sensibilité diminue, et inversement.

Pour comprendre pourquoi, revenons à l'exemple de la fraude. 

La plupart des fraudes ont été détectées, mais il y a eu de nombreux faux positifs. Supposons que, suite à des réclamations de clients, la direction ait décidé de relever le seuil de décision de 0,7 à 0,8. Pour qu'une transaction soit signalée comme frauduleuse, elle doit désormais obtenir un score d'au moins 0,8 au lieu de 0,7.

Cela a rendu le modèle plus prudent. Il a détecté moins de fraudes. Moins de transactions ont été signalées à tort comme frauduleuses, mais au prix d'un plus grand nombre de cas réellement frauduleux qui ont échappé à la détection. Après avoir modifié le seuil, le nombre de faux positifs a diminué de 300 à 60, mais le nombre de faux négatifs a augmenté de 40 à 80. 

La matrice de confusion du nouveau modèle se présente comme suit:

Comme nous pouvons le constater, 120 des 180 cas de fraude prédits étaient effectivement frauduleux, ce qui signifie que la précision est passée de 34,8 % à 66,7 %. 

Le prix à payer pour cette précision accrue réside dans une réduction du taux de rappel : 120 des 200 cas frauduleux ont été identifiés comme tels, ce qui signifie que le taux de rappel est passé de 80 % à seulement 60 %.

Le modèle détecte désormais moins de cas de fraude dans l'ensemble, mais lorsqu'il signale une fraude, il est beaucoup plus fiable. Cela nous démontre l'importance d'équilibrer ces deux indicateurs, ce que nous aborderons ultérieurement. 

La courbe précision-rappel

Pour visualiser le compromis entre précision et rappel, les scientifiques des données utilisent la courbe précision-rappels (PR). 

Ce graphique présente la précision sur l'axe des y et le rappel sur l'axe des x pour chaque seuil de décision possible (de 0 à 1). Lorsque vous abaissez le seuil afin de détecter davantage de cas positifs (augmentation du rappel), vous signalez inévitablement davantage de fausses alertes (diminution de la précision). 

Le modèle « idéal » atteindrait le coin supérieur droit (100 % de précision et de rappel), mais en réalité, il est nécessaire de sélectionner un point sur cette courbe qui répond aux exigences spécifiques de votre entreprise.

Dans notre exemple de fraude, nous disposons d'un modèle qui génère un score de fraude pour chaque transaction. Si le score d'une transaction atteint au moins le seuil défini, celle-ci est signalée comme frauduleuse. En abaissant le seuil, nous obtenons davantage de résultats positifs prédits, ce qui permet généralement de détecter davantage de résultats positifs réels (augmentation du rappel), mais également davantage de fausses alertes (diminution de la précision).

Voyons comment cela pourrait se présenter dans la pratique. Supposons que votre entreprise traite 10 000 transactions par jour. Étant donné que le taux de fraude est estimé à 2 %, vous pouvez vous attendre à 200 transactions frauduleuses par jour. Supposons également que l'équipe chargée de la lutte contre la fraude puisse examiner 200 transactions signalées (prédites positives) par jour.

Vous évaluez quelques seuils et obtenez les résultats suivants :

• Avec un seuil de 0,9, on obtient 100 résultats positifs prédits, avec une précision de 0,8 (80 fraudes réelles, 20 fausses alertes) et un rappel de 0,4 (vous détectez 80 cas de fraude sur 200). Vous n'utilisez pas pleinement votre capacité, car vous ne signalez que 100 cas par jour alors que vous pourriez en examiner 200. 
• Avec un seuil de 0,5, on obtient 500 résultats positifs prédits, avec une précision de 0,35 (175 fraudes réelles, 325 fausses alertes) et un rappel de 0,875 (vous détectez 175 cas de fraude sur 200). À ce stade, vous avez dépassé votre capacité, car il vous est impossible d'examiner 500 cas signalés.
• Avec un seuil de 0,7, on obtient 200 résultats positifs prédits, avec une précision de 0,6 (120 fraudes réelles, 80 fausses alertes) et un rappel de 0,6 (vous détectez 120 des 200 cas de fraude). Il s'agit probablement du seuil que vous utiliserez, car vous pouvez exploiter la pleine capacité tout en obtenant un rappel relativement satisfaisant de 0,6.

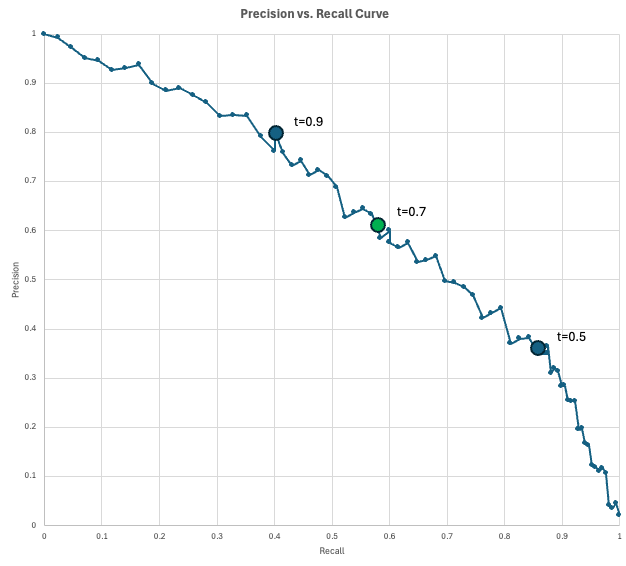
La courbe indique le niveau de précision que l'on peut obtenir pour un taux de rappel donné (ou inversement).

Quand utiliser la précision par rapport à la Rappel

En raison du compromis entre précision et rappel, la métrique appropriée dépend de votre cas d'utilisation particulier.

Quand utiliser la précision

Il existe une relation inverse entre la précision et les faux positifs. Par conséquent, un modèle précis est un modèle qui distingue correctement les vrais positifs des faux positifs. , c'estune valeur sûre.

Optimisez la précision lorsque le coût d'un faux positif est élevé. Voici quelques exemples de cas :

• Actions irréversibles : Systèmes automatisés de justice ou de suspension de comptes. Accuser une personne innocente ou supprimer définitivement le compte d'un utilisateur en raison d'une erreur de modèle (faux positif) peut causer des dommages irréparables.
• Interventions à coût élevé : Effectuer des forages pétroliers ou procéder à la fermeture d'une chaîne de montage dans une usine. Si agir sur la base d'une prévision positive implique des coûts de plusieurs millions de dollars, il est essentiel de s'assurer que cette prévision est correcte avant de poursuivre.
• Filtrage des spams : Boîtes de réception des e-mails. Il est regrettable de recevoir un courrier indésirable (faux négatif), mais il est inacceptable qu'une offre d'emploi importante soit envoyée dans le dossier des courriers indésirables (faux positif).

Quand utiliser le rappel

De même, il existe une relation inverse entre le rappel et les faux négatifs. De nombreux faux négatifs entraînent un faible taux de rappel. Par conséquent, un modèle présentant un rappel élevé distingue correctement les vrais positifs des faux négatifs. Il estsécurisé pour l' .

Si il est plus important d'éviter de passer à côté d'un cas réel que d'accepter des fausses alertes, il est recommandé de privilégier le taux de rappel plutôt que la précision. Voici quelques exemples d'utilisation :

• Sécurité médicale : Dépistage de maladies (par exemple, cancer ou septicémie). Passer à côté d'un patient malade peut être fatal, tandis qu'une fausse alerte entraîne des examens supplémentaires, ce qui représente un coût acceptable.
• Cybersécurité : Détection de logiciels malveillants ou intrusion dans le réseau. Il est préférable de signaler quelques connexions inoffensives comme suspectes plutôt que de laisser un seul pirate informatique compromettre le système sans être détecté.
• Qualité de fabrication : Détection des défauts. L'expédition d'un produit défectueux (faux négatif) entraîne des risques en matière de sécurité et peut nuire à la réputation. Il est donc préférable de rejeter quelques articles douteux plutôt que de laisser passer un produit défectueux.

Score F1 pour équilibrer la précision et le rappel

Si vous hésitez entre optimiser un modèle pour la précision ou le rappel, ou si vous souhaitez simplement prendre les deux en compte, vous pouvez vous référer au score F1. 

Le score F1 est défini comme la moyenne harmonique de la précision et du rappel, et est utilisé lorsque l'on souhaite atteindre un équilibre entre ces deux mesures. 

Si la précision et le rappel sont égaux, le score F1 est égal à cette valeur. Si l'un des deux tend vers zéro, cependant, F1 sera également très faible.

Dans l'exemple ci-dessus, la précision est de 66,7 % et le rappel est de 60 %. En utilisant la formule mentionnée ci-dessus, nous obtenons un score F1 d'environ 63,2 % :

Le tableau suivantcompare le score F1 à la précision, l'exactitude et le rappel.

Calcul de la précision et du rappel en Python

Il existe plusieurs méthodes pour calculer la précision, le rappel et le score F1 en Python. Dans ce qui suit, je présenterai deux approches : l'application directe des formules et l'utilisation des formules désignées dans le package scikit-learn.

Calculer la précision et le rappel à l'aide des formules

Si vous connaissez les chiffres de la matrice de confusion, vous pouvez facilement calculer les métriques à l'aide des formules présentées ci-dessus.

# Confusion matrix numbers
TP = 120
FP = 60
FN = 80
TN = 9740

# Formulas
precision = TP / (TP + FP)
recall = TP / (TP + FN)
f1 = 2 * precision * recall / (precision + recall)

# Output
print(f"{'Precision':<10} {precision:.1%}")
print(f"{'Recall':<10} {recall:.1%}")
print(f"{'F1':<10} {f1:.1%}")

Precision	66.7%
Recall		60.0%
F1		63.2%

Le résultat de ce code correspond à nos calculs précédents.

Calcul de la précision et du rappel à l'aide de scikit-learn

Vous pouvez également vous familiariser avec la bibliothèque scikit-learn afin de calculer des métriques à partir des données elles-mêmes. Dans l'exemple suivant, nous simulons y_true et y_predicted. Nous calculons ensuite la précision à l'aide de la méthode precision_score(y_true, y_false). Nous calculons le rappel et le score F1 de manière similaire. Enfin, nous allons afficher les résultats.

import numpy as np
from sklearn.metrics import precision_score, recall_score, f1_score

# Simulate Data (y_true and y_pred)
TP, FP, FN, TN = 120, 60, 80, 9740
y_true = np.array(TP * [1] + FP * [0] + FN * [1] + TN * [0])
y_pred = np.array(TP * [1] + FP * [1] + FN * [0] + TN * [0])

# Compute metrics with scikit-learn
precision = precision_score(y_true, y_pred, zero_division=0)
recall = recall_score(y_true, y_pred, zero_division=0)
f1 = f1_score(y_true, y_pred, zero_division=0)

# Print aligned output using f-strings (no manual spaces, no colon)
print(f"{'Precision':<10} {precision:.1%}")
print(f"{'Recall':<10} {recall:.1%}")
print(f"{'F1':<10} {f1:.1%}")

Precision	66.7%
Recall		60.0%
F1		63.2%

Comme prévu, ces chiffres concordent avec nos calculs antérieurs.

Conclusion

Bien que la précision soit un point de départ utile, elle masque souvent les détails nécessaires pour comprendre pourquoi un modèle échoue. La précision et le rappel vous offrent une vision plus claire en vous obligeant à examiner le compromis entre les fausses alertes et les détections manquées. 

En fin de compte, choisir la bonne mesure n'est pas seulement un problème mathématique ; il s'agit d'une décision pratique concernant le type d'erreur que votre système peut se permettre de commettre.

Êtes-vous prêt à créer vos propres modèles d'apprentissage automatique ? Commencez par les cours « Principes fondamentaux du machine learning en Python » cursus de compétence aujourd'hui!