Precisión frente a recuperación: La guía esencial para machine learning

Un modelo de machine learning con una precisión del 98 % suena impresionante, pero ¿lo es realmente? Cuando se trata de sucesos poco frecuentes, como el fraude o las enfermedades, la precisión suele crear una falsa sensación de seguridad.

Ahí es donde entran en juego la precisión y la recuperación. En este artículo, analizaremos cómo estas dos métricas van más allá de la simple precisión para medir no solo la frecuencia con la que aciertas, sino también cómo te equivocas exactamente.

Si deseas ir más allá de la teoría y dominar la clasificación, el curso Detección de fraudes en Python es el siguiente paso perfecto.

Por qué la precisión no es suficiente

En la mayoría de los casos, la precisión es la métrica natural que se utiliza para medir la capacidad de un modelo estadístico o de machine learning para predecir una determinada etiqueta. Se calcula comparando el número de casos predichos correctamente con el número total de observaciones. 

En términos generales, si un modelo identifica sistemáticamente la etiqueta correcta con gran precisión, significa que funciona bien. Sin embargo, los conjuntos de datos desequilibrados, en los que una clase contiene un número significativamente mayor de muestras que la otra, distorsionan la precisión. Estos conjuntos de datos son habituales en la detección de fraudes o el diagnóstico de enfermedades.

Supongamos que un modelo clasifica el fraude con una tasa de precisión del 98 %. A primera vista, esta tasa parece fantástica. Pero, ¿qué pasa si el fraude solo representa el 2 % de las transacciones del conjunto de datos? En este caso, un modelo podría elegir «no es fraude» cada vez y seguir obteniendo esa tasa de precisión del 98 % sin detectar ningún fraude, lo cual no es lo que queremos. 

Es evidente que este tipo de situaciones requieren métricas más matizadas. Dos métricas que se utilizan habitualmente sonla precisión y la recuperación ( ). 

¿Qué son la precisión y la recuperación?

Aquí tienes la versión resumida:

• Precisión (calidad): Mide la fiabilidad de tus predicciones positivas. Si el modelo dice «fraude», ¿se trata realmente de un fraude?
• Recuerdo (cantidad): Mide qué tan bien capturaste los casos positivos reales. ¿El modelo detectó todos los fraudes o se te escaparon algunos?

Sin embargo, para comprender cómo calcular estas métricas, primero debemos definir la terminología utilizada en una matriz de confusión.

Verdaderos positivos, falsos positivos y negativos 

Considera una empresa de tarjetas de crédito que utiliza un modelo de machine learning para detectar transacciones fraudulentas con tarjetas de crédito. Supongamos que, de una muestra de 10 000 transacciones, 9800 eran legítimas y 200 eran fraudulentas.

Para medir la eficacia del modelo, designa uno de los casos como «fraude» o «no fraude» como caso positivo y el otro como caso negativo. Dado que los casos de fraude son de interés, etiquétalos como casos «positivos». (Por supuesto, esto no implica que el fraude sea positivo en un sentido ético; la etiqueta «positivo» solo indica el caso que nos interesa).

Cuando se ejecuta el modelo, las transacciones con una puntuación de riesgo superior a un umbral de probabilidad determinado, por ejemplo, el 70 %, se consideran fraudulentas. Los casos que se prevé que sean fraudulentos se comparan con los que realmente lo son.

Para mantener todos estos datos en orden, utilizamos la siguiente nomenclatura. 

• Verdaderos Positivos (VP): Se predijo correctamente que 160 casos eran fraudes.
• Verdaderos Negativos (VN): Se identificaron correctamente 9500 casos como no fraudulentos.
• Falsos positivos (FP): 300 casos fueron incorrectamente señalados como fraude.
• Falsos negativos (FN): 40 casos se marcaron incorrectamente como no fraudulentos.

La segunda letra (P o N) indica si la predicción fue positiva o negativa, y la primera letra muestra si esa predicción fue verdadera (T) o falsa (F). 

Un «falso positivo» indica que el sistema predijo que el caso era positivo, pero en realidad era negativo. Por ejemplo, un falso negativo es un caso que se predijo que era negativo, pero que en realidad es positivo.

Matriz de confusión

Toda esta información se muestra habitualmente en la denominada matriz de confusión, que programa la frecuencia con la que el modelo confunde predicciones incorrectas con resultados reales (FN, FP). La matriz de confusión nos ayuda a distinguir entre lo que predijo el modelo y lo que realmente ocurrió. La matriz de confusión de nuestro ejemplo tiene el siguiente aspecto: this:

Ahora, echemos un vistazo a los totales de filas y columnas. Las sumas de las filas indican el total de casos previstos, y las sumas de las columnas indican el total de casos reales.

¿Qué representan estos totales?

• El total de la primera fila (460) representa el número total de casos de fraude previstos (TP + FP).
• El total de la segunda fila (9540) representa el número total de casos legítimos previstos (FN + TN).
• El total de la primera columna (200) representa el número total de casos reales de fraude (TP + FN).
• El total de la segunda columna (9800) representa el número total de casos legítimos reales (FP + TN).
• El total general (10 000) equivale al tamaño total de nuestra muestra.

¿Qué es la precisión?

La precisión ( ) mide la calidad de tus predicciones positivas. Nos indica cuántos casos que se predijo que serían positivos resultaron ser realmente positivos. 

Un modelo preciso significa tener muy pocas falsas alarmas. Si el modelo dice que algo es cierto, lo más probable es que sea cierto. Por ejemplo, si un juego en línea expulsa a alguien por hacer trampa, tiene que ser cierto. Demasiadas prohibiciones inmerecidas alejan a los usuarios legítimos y dan lugar a críticas negativas. 

En la terminología examinada anteriormente, la precisión es igual a la relación entre los verdaderos positivos y los positivos predichos.

En el ejemplo anterior, la precisión es 160/460, o aproximadamente el 34,8 %.

¿Qué es la retirada de productos?

Recordemos las medidas de cobertura de. Nos muestra cuántos de los resultados positivos reales se predijeron como tales. Se define como la relación entre los verdaderos positivos y el total de positivos reales.

Considera los diagnósticos de cáncer para el seguimiento inicial. ¿Es mejor pecar por exceso de diagnóstico o por defecto? La mayoría de la gente estaría de acuerdo con lo primero. 

En el caso de las pruebas de detección precoz, recibir una falsa alarma puede resultar impactante. Pero es catastrófico que te digan que no tienes cáncer cuando en realidad sí lo tienes, sobre todo teniendo en cuenta que podrías perderte un tratamiento que podría salvarte la vida.

En el ejemplo anterior, la recuperación es de 160/200, o del 80 %.

La disyuntiva entre precisión y recuperación

Existe una relación de tira y afloja entre la precisión y la recuperación. Por lo general, a medida que aumenta la precisión, disminuye la recuperación, y viceversa.

Para entender por qué, volvamos al ejemplo del fraude. 

Se detectaron la mayoría de los fraudes, pero hubo muchos falsos positivos. Digamos que, debido a las quejas de los clientes, la dirección decidió aumentar el umbral de decisión de 0,7 a 0,8. Para que una transacción sea marcada como fraudulenta, ahora debe tener una puntuación mínima de 0,8 en lugar de 0,7.

Esto hizo que el modelo fuera más conservador. Predijo el fraude con menos frecuencia. Se señalaron menos transacciones como fraudulentas por error, pero a costa de que se pasaran por alto más casos realmente fraudulentos. Después de cambiar el umbral, el número de falsos positivos disminuyó de 300 a 60, pero el número de falsos negativos aumentó de 40 a 80. 

La matriz de confusión del nuevo modelo tiene el siguiente aspecto:

Como podemos ver, 120 de los 180 casos de fraude previstos eran realmente fraudulentos, por lo que la precisión aumentó del 34,8 % al 66,7 %. 

El precio de esta mayor precisión radica en una reducción de la sensibilidad: Se predijeron 120 de los 200 casos fraudulentos, lo que significa que la recuperación pasó del 80 % original al 60 % actual.

Ahora, el modelo detecta menos casos de fraude en general, pero cuando lo hace, es mucho más fiable. Esto nos muestra la importancia de equilibrar ambas métricas, tema que trataremos más adelante. 

La curva de precisión-recuerdo

Para visualizar la relación entre precisión y recuperación, los científicos de datos utilizan la curva de precisión-recuerdo (PR). 

Este gráfico gráficando la precisión en el eje Y y la recuperación en el eje X para cada umbral de decisión posible (de 0 a 1). A medida que se reduce el umbral para capturar más casos positivos (aumentando la sensibilidad), inevitablemente se marcan más falsas alarmas (disminuyendo la precisión). 

El modelo «perfecto» alcanzaría la esquina superior derecha (100 % de precisión y recuperación), pero en realidad debes elegir un punto en esta curva que satisfaga tus requisitos comerciales específicos.

En nuestro ejemplo de fraude, tenemos un modelo que genera una puntuación de fraude para cada transacción. Si la puntuación de una transacción alcanza al menos el umbral, se marca como fraude. A medida que reducimos el umbral, obtenemos más positivos predichos, lo que normalmente captura más positivos verdaderos (aumentando la recuperación), pero también más falsas alarmas (disminuyendo la precisión).

Veamos cómo se vería todo esto en la práctica. Supongamos que tu empresa procesa 10 000 transacciones al día. Dado que la tasa de fraude se estima en un 2 %, se esperan 200 transacciones fraudulentas al día. Además, supongamos que el equipo de operaciones contra el fraude puede revisar 200 transacciones marcadas (positivos previstos) al día.

Evalúas varios umbrales y obtienes estos resultados:

• Con un umbral de 0,9, hay 100 positivos previstos, con una precisión de 0,8 (80 fraudes reales, 20 falsas alarmas) y una recuperación de 0,4 (detectas 80 de los 200 casos de fraude). No estás aprovechando al máximo tu capacidad, ya que solo marcas 100 al día cuando podrías revisar 200 al día. 
• Con un umbral de 0,5, hay 500 positivos previstos, con una precisión de 0,35 (175 fraudes reales, 325 falsas alarmas) y una recuperación de 0,875 (se detectan 175 de los 200 casos de fraude). En este umbral, estás por encima de la capacidad, ya que no puedes revisar 500 casos marcados.
• Con un umbral de 0,7, hay 200 positivos previstos, con una precisión de 0,6 (120 fraudes reales, 80 falsas alarmas) y una recuperación de 0,6 (se detectan 120 de los 200 casos de fraude). Probablemente este sea el umbral que utilices, ya que puedes aprovechar toda la capacidad y seguir obteniendo una recuperación bastante aceptable de 0,6.

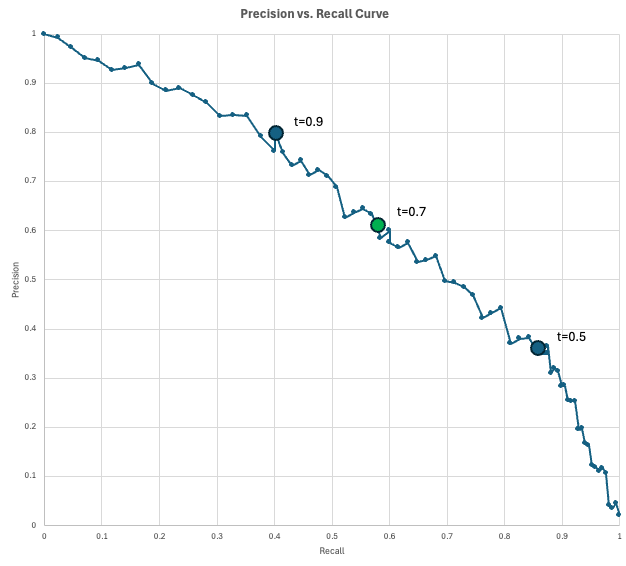
La curva indica la precisión que puedes obtener con una tasa de recuperación determinada (o viceversa).

Cuándo utilizar precisión frente a Recordatorio

Debido a la relación de compensación entre precisión y recuperación, la métrica correcta depende de tu caso de uso particular.

Cuándo utilizar la precisión

Existe una relación inversa entre la precisión y los falsos positivos. Por lo tanto, un modelo preciso es aquel que diferencia correctamente entre verdaderos positivos y falsos positivos. Es confiable.

Optimiza la precisión cuando el coste de un falso positivo sea elevado. Algunos ejemplos de casos son:

• Acciones irreversibles: Sistemas automatizados de justicia o de bloqueo de cuentas. Acusar a una persona inocente o eliminar permanentemente la cuenta de un usuario debido a un error del modelo (falso positivo) causa un daño irreparable.
• Intervenciones de alto costo: Perforar en busca de petróleo o cerrar la cadena de montaje de una fábrica. Si actuar en base a una predicción positiva cuesta millones de dólares, debes asegurarte de que la predicción sea correcta antes de seguir adelante.
• Filtrado de spam: Bandejas de entrada de correo electrónico. Es molesto recibir un correo electrónico no deseado (falso negativo), pero es inaceptable que una oferta de trabajo importante se envíe a la carpeta de correo no deseado (falso positivo).

Cuándo utilizar la función de recuperación

Del mismo modo, existe una relación inversa entre la recuperación y los falsos negativos. Muchos falsos negativos provocan un bajo nivel de recuperación. Por consiguiente, un modelo con un alto nivel de recuperación distingue correctamente entre los verdaderos positivos y los falsos negativos. Es seguro.

Si es más importante evitar pasar por alto un caso real que aceptar falsas alarmas, debes dar prioridad a la métrica de recuperación sobre la precisión. Algunos ejemplos de casos de uso son:

• Seguridad médica: Detección de enfermedades (por ejemplo, cáncer o sepsis). Pasar por alto a un paciente enfermo puede ser fatal, mientras que una falsa alarma lleva a más pruebas, lo cual es un costo tolerable.
• Ciberseguridad: Detección de malware o intrusión en la red. Es mejor marcar algunos inicios de sesión inocentes como sospechosos que permitir que un solo hacker infrinja el sistema sin ser detectado.
• Calidad de fabricación: Detección de defectos. El envío de un producto defectuoso (falso negativo) genera responsabilidades en materia de seguridad y daña la reputación, por lo que es mejor descartar algunos artículos dudosos que dejar pasar uno defectuoso.

Puntuación F1 para equilibrar la precisión y la recuperación

Si no estás seguro de si optimizar un modelo para la precisión o la recuperación, o simplemente quieres tener en cuenta ambas cosas, puedes consultar la puntuación F1. 

El puntuación F1 se define como la media armónica de la precisión y la recuperación, y se utiliza cuando se desea lograr un equilibrio entre ambas métricas. 

Si la precisión y la recuperación son iguales, la puntuación F1 es igual a ese valor. Sin embargo, si uno de los dos se aproxima a cero, F1 también será muy bajo.

En el ejemplo anterior, la precisión es del 66,7 % y la recuperación es del 60 %. Utilizando la fórmula mencionada anteriormente, obtenemos una puntuación F1 de aproximadamente el 63,2 %:

La siguiente tablacompara la puntuación F1 con la exactitud, la precisión y la recuperación.

Cálculo de la precisión y la recuperación en Python

Hay muchas formas de calcular la precisión, la recuperación y la puntuación F1 en Python. A continuación, presentaré dos enfoques: aplicar las fórmulas directamente y utilizar fórmulas designadas en el paquete scikit-learn.

Cálculo de la precisión y la recuperación utilizando las fórmulas

Si conoces los números de la matriz de confusión, puedes calcular fácilmente las métricas utilizando las fórmulas presentadas anteriormente.

# Confusion matrix numbers
TP = 120
FP = 60
FN = 80
TN = 9740

# Formulas
precision = TP / (TP + FP)
recall = TP / (TP + FN)
f1 = 2 * precision * recall / (precision + recall)

# Output
print(f"{'Precision':<10} {precision:.1%}")
print(f"{'Recall':<10} {recall:.1%}")
print(f"{'F1':<10} {f1:.1%}")

Precision	66.7%
Recall		60.0%
F1		63.2%

El resultado de este código coincide con nuestros cálculos anteriores.

Cálculo de la precisión y la recuperación utilizando scikit-learn

También puedes aprender a utilizar la biblioteca scikit-learn para calcular métricas a partir de los propios datos. En el siguiente ejemplo, simulamos y_true y y_predicted. A continuación, calculamos la precisión utilizando el método precision_score(y_true, y_false). Calculamos la recuperación y la puntuación F1 de manera similar. Por último, mostraremos los resultados.

import numpy as np
from sklearn.metrics import precision_score, recall_score, f1_score

# Simulate Data (y_true and y_pred)
TP, FP, FN, TN = 120, 60, 80, 9740
y_true = np.array(TP * [1] + FP * [0] + FN * [1] + TN * [0])
y_pred = np.array(TP * [1] + FP * [1] + FN * [0] + TN * [0])

# Compute metrics with scikit-learn
precision = precision_score(y_true, y_pred, zero_division=0)
recall = recall_score(y_true, y_pred, zero_division=0)
f1 = f1_score(y_true, y_pred, zero_division=0)

# Print aligned output using f-strings (no manual spaces, no colon)
print(f"{'Precision':<10} {precision:.1%}")
print(f"{'Recall':<10} {recall:.1%}")
print(f"{'F1':<10} {f1:.1%}")

Precision	66.7%
Recall		60.0%
F1		63.2%

Como era de esperar, estas cifras coinciden con nuestros cálculos anteriores.

Conclusión

Aunque la precisión es un punto de partida útil, a menudo oculta los detalles que necesitas para comprender por qué un modelo está fallando. La precisión y la recuperación te ofrecen una imagen más clara al obligarte a analizar la relación entre las falsas alarmas y las detecciones perdidas. 

En última instancia, elegir la métrica adecuada no es solo un problema matemático, sino una decisión práctica sobre qué tipo de error puede permitirse cometer tu sistema.

¿Estás listo para crear tus propios modelos de machine learning? Comienza con los Fundamentos del machine learning en Python hoy mismo.