Precisão vs. Recuperação: O Guia Essencial para Machine Learning

Um modelo de machine learning com 98% de precisão parece incrível, mas será que é mesmo? Quando você está lidando com coisas raras, tipo fraude ou doença, a precisão muitas vezes cria uma falsa sensação de segurança.

É aí que entram a precisão e a recuperação. Neste artigo, vamos ver como essas duas métricas vão além da simples precisão para medir não só a frequência com que você acerta, mas exatamente como você erra.

Se você quer ir além da teoria e dominar a classificação, o curso Detecção de Fraudes em Python é o próximo passo perfeito.

Por que a precisão não é suficiente

Na maioria das vezes, a precisão é a medida natural usada pra ver como um modelo estatístico ou de machine learning prevê um determinado rótulo. É calculado comparando o número de instâncias previstas corretamente com o número total de observações. 

Em geral, se um modelo sempre identifica o rótulo certo com muita precisão, ele tá funcionando bem. Mas, conjuntos de dados desequilibrados, em que uma classe tem muito mais amostras do que a outra, podem atrapalhar a precisão. Esses conjuntos de dados são comuns na detecção de fraudes ou no diagnóstico de doenças.

Vamos supor que um modelo identifique fraudes com uma precisão de 98%. À primeira vista, essa taxa parece incrível. Mas e se a fraude só for responsável por 2% das transações no conjunto de dados? Nesse caso, um modelo poderia escolher “não fraude” todas as vezes e ainda assim obter essa taxa de precisão de 98%, sem detectar nenhuma fraude, o que não é o que queremos. 

Claro, esse tipo de situação precisa de métricas mais detalhadas. Duas métricas comumente usadas sãoa precisão e a recuperação ( ). 

O que são precisão e recall?

Aqui vai a versão resumida:

• Precisão (Qualidade): Mede o quanto suas previsões positivas são confiáveis. Se o modelo diz “fraude”, é mesmo fraude?
• Recall (Quantidade): Mede o quão bem você capturou os casos positivos reais. O modelo detectou todas as fraudes ou algumas passaram despercebidas?

Mas, pra entender como calcular essas métricas, primeiro precisamos definir a terminologia usada numa matriz de confusão.

Verdadeiro positivo, falso positivo e negativos 

Pense numa empresa de cartão de crédito que usa um modelo de machine learning pra detectar transações fraudulentas com cartão de crédito. Digamos que, numa amostra de 10.000 transações, 9.800 eram legítimas e 200 eram fraudes.

Para ver se o modelo funciona, escolha um deles como caso positivo (fraude ou não fraude) e o outro como caso negativo. Como os casos de fraude são interessantes, vamos chamá-los de casos “positivos”. (Isso, claro, não quer dizer que a fraude seja boa no sentido ético; o rótulo “positivo” só mostra em qual caso estamos interessados.)

Quando o modelo é executado, as transações com uma pontuação de risco acima de um certo limite de probabilidade, digamos 70%, são consideradas fraudulentas. Os casos que acham que são fraudulentos são comparados com os que realmente são.

Para manter todos esses dados organizados, usamos a seguinte nomenclatura. 

• Verdadeiros positivos (TP): 160 casos de fraude foram corretamente identificados como tal.
• Verdadeiros negativos (TN): 9.500 casos foram corretamente identificados como não fraudulentos.
• Falsos positivos (FP): 300 casos foram marcados como fraude por engano.
• Falsos negativos (FN): 40 casos foram marcados de forma errada como não sendo fraude.

A segunda letra (P ou N) mostra se a previsão foi positiva ou negativa, e a primeira letra mostra se essa previsão foi verdadeira (V) ou falsa (F). 

Um “falso positivo” quer dizer que o sistema achou que o caso era positivo, mas na verdade era negativo. Por exemplo, um falso negativo é um caso que foi previsto como negativo, mas na verdade é positivo.

Matriz de confusão

Todas essas informações geralmente aparecem na chamada matriz de confusão, que programa a frequência com que o modelo confunde previsões incorretas com resultados reais (FN, FP). A matriz de confusão nos ajuda a ver a diferença entre o que o modelo previu e o que realmente aconteceu. A matriz de confusão do nosso exemplo fica assim:his:

Agora,, vamos dar uma olhada nos totais das linhas e colunas. As somas das linhas mostram o total de casos previstos, e as somas das colunas mostram o total de casos reais.

O que esses totais representam?

• A primeira linha total (460) mostra o número total de casos de fraude previstos (TP + FP).
• A segunda linha total (9.540) mostra o número total de casos legítimos previstos (FN + TN).
• O total da primeira coluna (200) mostra o número total de casos reais de fraude (TP + FN).
• O total da segunda coluna (9.800) mostra o número total de casos legítimos reais (FP + TN).
• O total geral (10.000) é igual ao tamanho total da nossa amostra.

O que é precisão?

A precisão ( ) mede a qualidade das suas previsões positivas. Isso mostra quantos casos que a gente achava que eram positivos realmente eram positivos. 

Um modelo preciso significa ter muito poucos alarmes falsos. Se o modelo diz que algo é verdade, provavelmente é verdade. Por exemplo, se um jogo online bane alguém por trapaça, isso precisa ser verdade. Muitas proibições injustificadas afastam os usuários legítimos e geram críticas negativas. 

Na terminologia que vimos acima, a precisão é igual à proporção de verdadeiros positivos em relação aos positivos previstos.

No exemplo acima, a precisão é 160/460, ou cerca de 34,8%.

O que é recall?

Lembre-se de que mede a cobertura. Isso mostra quantos dos resultados positivos reais foram previstos como tal. É a relação entre os verdadeiros positivos e o total de positivos reais.

Pense nos diagnósticos de câncer para o acompanhamento inicial. É melhor errar por excesso de diagnóstico ou por falta de diagnóstico? A maioria das pessoas concordaria com a primeira opção. 

No caso de exames de rastreamento precoce, pode ser chocante receber um falso alarme. Mas é péssimo quando te dizem que você não tem câncer, quando na verdade você tem, principalmente porque você pode acabar perdendo um tratamento que poderia salvar sua vida.

No exemplo acima, a recuperação é de 160/200, ou 80%.

O equilíbrio entre precisão e recuperação

Tem uma relação de equilíbrio entre precisão e recall. Normalmente, quanto mais precisa fica, menos lembrança tem, e vice-versa.

Para entender o motivo, vamos revisitar o exemplo da fraude. 

A maioria das fraudes foi detectada, mas houve muitos falsos positivos. Digamos que, por causa das reclamações dos clientes, a gerência decidiu aumentar o limite de decisão de 0,7 para 0,8. Para uma transação ser sinalizada como fraude, agora ela precisa ter uma pontuação de pelo menos 0,8 em vez de 0,7.

Isso deixou o modelo mais conservador. Ele previu fraudes com menos frequência. Menos transações foram sinalizadas incorretamente como fraude, mas isso fez com que mais casos realmente fraudulentos passassem despercebidos. Depois de mudar o limite, o número de falsos positivos caiu de 300 para 60, mas o número de falsos negativos subiu de 40 para 80. 

A matriz de confusão do novo modelo é assim:

Como dá pra ver, 120 dos 180 casos de fraude previstos eram realmente fraudulentos, então a precisão aumentou de 34,8% para 66,7%. 

O preço dessa maior precisão está na redução da taxa de recall: 120 dos 200 casos fraudulentos foram previstos como tal, o que significa que a taxa de recuperação caiu de 80% originalmente para apenas 60% agora.

Agora, o modelo detecta menos casos de fraude no geral, mas quando sinaliza uma fraude, é muito mais confiável. Isso mostra como é importante equilibrar as duas métricas, assunto que vamos abordar mais tarde. 

A curva de precisão-recall

Para visualizar o equilíbrio entre precisão e recall, os cientistas de dados usam a curva de precisão-recall (PR). 

Este gráfico mostra a precisão no eixo y e a recuperação no eixo x para cada limite de decisão possível (de 0 a 1). À medida que você diminui o limite para capturar mais casos positivos (aumentando a recuperação), você inevitavelmente sinaliza mais alarmes falsos (diminuindo a precisão). 

O modelo “perfeito” chegaria ao canto superior direito (100% de precisão e recuperação), mas, na verdade, você precisa escolher um ponto nessa curva que atenda às suas necessidades específicas de negócio.

No nosso exemplo de fraude, temos um modelo que gera uma pontuação de fraude para cada transação. Se a pontuação de uma transação for pelo menos igual ao limite, ela será marcada como fraude. À medida que diminuímos o limiar, obtemos mais resultados positivos previstos, o que normalmente captura mais resultados positivos verdadeiros (aumentando a recuperação), mas também mais alarmes falsos (diminuindo a precisão).

Vamos ver como tudo isso pode funcionar na prática. Imagina que sua empresa processa 10.000 transações por dia. Como a taxa de fraude é estimada em 2%, você espera 200 transações fraudulentas por dia. Além disso, digamos que a equipe de operações de fraude consiga analisar 200 transações sinalizadas (positivas previstas) por dia.

Você avalia alguns limites e encontra estes resultados:

• Com um limite de 0,9, tem 100 resultados positivos previstos, com uma precisão de 0,8 (80 fraudes reais, 20 alarmes falsos) e uma recuperação de 0,4 (você pega 80 dos 200 casos de fraude). Você está subutilizando a capacidade porque sinaliza apenas 100 por dia, quando poderia revisar 200 por dia. 
• Com um limiar de 0,5, tem 500 positivos previstos, com uma precisão de 0,35 (175 fraudes reais, 325 falsos alarmes) e uma recuperação de 0,875 (você pega 175 dos 200 casos de fraude). Nesse limite, você está acima da capacidade, já que não dá pra revisar 500 casos sinalizados.
• Com um limite de 0,7, tem 200 resultados positivos previstos, com uma precisão de 0,6 (120 fraudes reais, 80 alarmes falsos) e uma recuperação de 0,6 (você pega 120 dos 200 casos de fraude). Esse provavelmente é o limite que você vai usar, já que dá pra usar toda a capacidade e ainda ter uma recuperação razoável de 0,6.

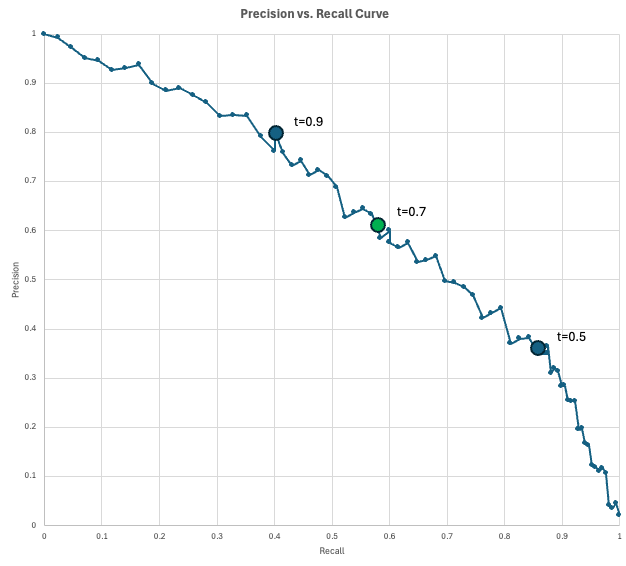
A curva mostra a precisão que você pode comprar com uma determinada taxa de recall (ou vice-versa).

Quando usar precisão vs. Lembre-se

Por causa da relação de compensação entre precisão e recuperação, a métrica certa depende do seu caso específico.

Quando usar a precisão

Tem uma relação inversa entre precisão e falsos positivos. Então, um modelo preciso é aquele que consegue diferenciar direitinho entre os verdadeiros positivos e os falsos positivos. É confiável.

Otimize a precisão quando o custo de um falso positivo for alto. Exemplos de casos incluem:

• Ações que não dá pra desfazer: Sistemas de justiça automatizada ou de banimento de contas. Acusar alguém inocente ou excluir pra sempre a conta de um usuário por causa de um erro no modelo (falso positivo) causa danos que não têm conserto.
• Intervenções de alto custo: Perfurar em busca de petróleo ou fechar uma linha de montagem de uma fábrica. Se agir com base em uma previsão positiva custa milhões de dólares, você precisa ter certeza de que a previsão está correta antes de seguir em frente.
• Filtragem de spam: Caixas de entrada de e-mail. É chato ver um e-mail de spam (falso negativo), mas é inaceitável que uma oferta de emprego importante vá parar na pasta de lixo eletrônico (falso positivo).

Quando usar o recall

Da mesma forma, existe uma relação inversa entre recall e falsos negativos. Muitos falsos negativos fazem com que a recuperação seja baixa. Então, um modelo com alta precisão consegue diferenciar direitinho entre os verdadeiros positivos e os falsos negativos. Éseguro usar o .

Se é mais importante evitar perder um caso real do que aceitar falsos alarmes, você deve priorizar a métrica de recall em vez da precisão. Exemplos de casos de uso incluem:

• Segurança médica: Rastreamento de doenças (por exemplo, câncer ou sepse). Deixar passar um paciente doente pode ser fatal, enquanto um falso alarme leva a mais exames, o que é um custo aceitável.
• Segurança cibernética: Detecção de malware ou invasão de rede. É melhor marcar alguns logins inocentes como suspeitos do que deixar um único hacker invadir o sistema sem ser detectado.
• Qualidade de fabricação: Detecção de defeitos. Enviar um produto com defeito (falso negativo) pode trazer problemas de segurança e arruinar a reputação, então é melhor descartar alguns itens duvidosos do que deixar um produto ruim passar.

Pontuação F1 para equilibrar precisão e recuperação

Se você não tem certeza se deve otimizar um modelo para precisão ou recall, ou simplesmente quer levar ambos em consideração, pode dar uma olhada na pontuação F1. 

O Pontuação F1 é a média harmônica da precisão e da recuperação, e é usada quando você quer um equilíbrio entre as duas métricas. 

Se a precisão e a recuperação forem iguais, a pontuação F1 é igual a esse valor. Se um dos dois se aproximar de zero, no entanto, F1 também será muito baixo.

No exemplo acima, a precisão é de 66,7% e a recuperação é de 60%. Usando a fórmula que falamos acima, a gente consegue uma pontuação F1 de mais ou menos 63,2%:

A tabela a seguircompara a pontuação F1 com a precisão, exatidão e recuperação.

Calculando precisão e recall em Python

Tem várias maneiras de calcular a precisão, a recuperação e a pontuação F1 no Python. A seguir, vou mostrar duas maneiras de fazer isso: aplicando as fórmulas diretamente e usando fórmulas específicas do pacote scikit-learn.

Calculando a precisão e a recuperação usando as fórmulas

Se você souber os números da matriz de confusão, pode calcular facilmente as métricas usando as fórmulas apresentadas acima.

# Confusion matrix numbers
TP = 120
FP = 60
FN = 80
TN = 9740

# Formulas
precision = TP / (TP + FP)
recall = TP / (TP + FN)
f1 = 2 * precision * recall / (precision + recall)

# Output
print(f"{'Precision':<10} {precision:.1%}")
print(f"{'Recall':<10} {recall:.1%}")
print(f"{'F1':<10} {f1:.1%}")

Precision	66.7%
Recall		60.0%
F1		63.2%

O resultado desse código bate com os nossos cálculos anteriores.

Calculando precisão e recuperação usando scikit-learn

Você também pode aprender a usar a biblioteca scikit-learn para calcular métricas a partir dos próprios dados. No exemplo a seguir, simulamos y_true e y_predicted. Depois, calculamos a precisão usando o método precision_score(y_true, y_false). A gente calcula o recall e o F1 score da mesma forma. Por fim, vamos apresentar os resultados.

import numpy as np
from sklearn.metrics import precision_score, recall_score, f1_score

# Simulate Data (y_true and y_pred)
TP, FP, FN, TN = 120, 60, 80, 9740
y_true = np.array(TP * [1] + FP * [0] + FN * [1] + TN * [0])
y_pred = np.array(TP * [1] + FP * [1] + FN * [0] + TN * [0])

# Compute metrics with scikit-learn
precision = precision_score(y_true, y_pred, zero_division=0)
recall = recall_score(y_true, y_pred, zero_division=0)
f1 = f1_score(y_true, y_pred, zero_division=0)

# Print aligned output using f-strings (no manual spaces, no colon)
print(f"{'Precision':<10} {precision:.1%}")
print(f"{'Recall':<10} {recall:.1%}")
print(f"{'F1':<10} {f1:.1%}")

Precision	66.7%
Recall		60.0%
F1		63.2%

Como era de se esperar, esses números batem com os nossos cálculos anteriores.

Conclusão

Embora a precisão seja um bom ponto de partida, muitas vezes ela esconde os detalhes necessários para entender por que um modelo está falhando. A precisão e a recuperação te dão uma visão mais clara, fazendo você pensar no equilíbrio entre alarmes falsos e detecções perdidas. 

No fim das contas, escolher a métrica certa não é só um problema de matemática; é uma decisão prática sobre que tipo de erro seu sistema pode se dar ao luxo de cometer.

Pronto pra criar seus próprios modelos de machine learning? Comece com o Fundamentos de Machine Learning em Python hoje mesmo!