Genauigkeit vs. Wiederauffindbarkeit: Der unverzichtbare Leitfaden für maschinelles Lernen

Ein Machine-Learning-Modell mit einer Genauigkeit von 98 % klingt echt beeindruckend – aber ist es das auch wirklich? Wenn du mit seltenen Sachen wie Betrug oder Krankheiten zu tun hast, kann Genauigkeit oft ein falsches Gefühl von Sicherheit geben.

Hier kommen Präzision und Recall ins Spiel. In diesem Artikel schauen wir uns an, wie diese beiden Kennzahlen über die einfache Genauigkeit hinausgehen und nicht nur messen, wie oft du richtig liegst, sondern auch, wie genau du falsch liegst.

Wenn du über die Theorie hinausgehen und die Klassifizierung richtig draufhaben willst, ist die Kurs „Betrugserkennung in Python“ der perfekte nächste Schritt.

Warum Genauigkeit nicht reicht

In den meisten Fällen ist die Genauigkeit der natürliche Maßstab, um zu messen, wie gut ein statistisches oder maschinelles Lernmodell ein bestimmtes Label vorhersagt. Die Berechnung erfolgt durch den Vergleich der Anzahl korrekt vorhergesagter Fälle mit der Gesamtzahl der Beobachtungen. 

Im Allgemeinen kann man sagen, dass ein Modell gut funktioniert, wenn es immer das richtige Label mit hoher Genauigkeit erkennt. Aber wenn die Datensätze unausgewogen sind, weil eine Klasse viel mehr Beispiele hat als die andere, wird die Genauigkeit beeinträchtigt. Solche Datensätze sind bei der Betrugsaufdeckung oder der Diagnose von Krankheiten üblich.

Nehmen wir mal an, ein Modell erkennt Betrug mit einer Genauigkeit von 98 %. Auf den ersten Blick klingt dieser Preis echt super. Aber was ist, wenn Betrug nur 2 % der Transaktionen im Datensatz ausmacht? In diesem Fall könnte ein Modell jedes Mal „kein Betrug“ wählen und trotzdem eine Genauigkeitsrate von 98 % erreichen, ohne einen einzigen Betrugsfall zu erkennen, was nicht das ist, was wir wollen. 

Klar, solche Situationen brauchen genauere Messgrößen. Zwei häufig verwendete Metriken sinddie Präzision und der Recallder . 

Was sind Präzision und Recall?

Hier ist die kurze Version:

• Genauigkeit (Qualität): Misst, wie zuverlässig deine positiven Vorhersagen sind. Wenn das Modell „Betrug“ sagt, ist es dann wirklich Betrug?
• Rückruf (Menge): Misst, wie gut du die tatsächlichen positiven Fälle erfasst hast. Hat das Modell alle Betrugsfälle abgefangen oder sind einige durchgerutscht?

Um zu verstehen, wie man diese Kennzahlen berechnet, müssen wir aber erst mal die Begriffe klären, die in einer Verwechslungsmatrix benutzt werden.

Echt positiv, falsch positiv und negativ 

Stell dir mal eine Kreditkartengesellschaft vor, die ein Machine-Learning-Modell nutzt, um betrügerische Kreditkartentransaktionen zu erkennen. Angenommen, bei einer Stichprobe von 10.000 Transaktionen gab es 9.800 legitime Transaktionen und 200 Fälle von Betrug.

Um zu sehen, wie gut das Modell funktioniert, machst du entweder „Betrug“ oder „kein Betrug“ zum positiven Fall und den anderen zum negativen Fall. Da die Betrugsfälle interessant sind, bezeichne diese als „positive“ Fälle. (Das heißt natürlich nicht, dass Betrug in ethischer Hinsicht gut ist; das Wort „positiv” zeigt nur, welcher Fall uns interessiert.)

Wenn das Modell läuft, werden Transaktionen mit einem Risikowert über einem bestimmten Schwellenwert, zum Beispiel 70 %, als Betrug angesehen. Die Fälle, bei denen man denkt, dass sie betrügerisch sind, werden mit denen verglichen, die es wirklich sind.

Um den Überblick über all diese Daten zu behalten, benutzen wir die folgende Nomenklatur. 

• Echte Positive (TP): 160 Betrugsfälle wurden richtig als Betrug erkannt.
• Echte Negative (TN): 9500 Fälle wurden richtig als nicht betrügerisch erkannt.
• Falsch-positive Ergebnisse (FP): 300 Fälle wurden fälschlicherweise als Betrug gemeldet.
• Falsch-negative Ergebnisse (FN): 40 Fälle wurden fälschlicherweise als nicht betrügerisch eingestuft.

Der zweite Buchstabe (P oder N) zeigt, ob die Vorhersage positiv oder negativ war, und der erste Buchstabe sagt, ob die Vorhersage richtig (T) oder falsch (F) war. 

Ein „falsch positives Ergebnis“ heißt, dass das System den Fall als positiv eingeschätzt hat, obwohl er eigentlich negativ war. Ein falsch negatives Ergebnis ist zum Beispiel ein Fall, bei dem das Ergebnis als negativ vorhergesagt wurde, obwohl es eigentlich positiv ist.

Verwechslungsmatrix

All diese Infos werden normalerweise in der sogenannten Verwirrungsmatrix, die zeigt, wie oft das Modell falsche Vorhersagen mit tatsächlichen Ergebnissen verwechselt (FN, FP). Die Verwechslungsmatrix hilft uns dabei, zwischen dem, was das Modell vorhergesagt hat, und dem, was tatsächlich passiert ist, zu unterscheiden. Die Verwechslungsmatrix in unserem Beispiel sieht so aus:his:

Schauen wir uns jetzt die Zeilen- und Spaltensummen an. Die Zeilensummen zeigen die Gesamtzahl der vorhergesagten Fälle an, und die Spaltensummen zeigen die Gesamtzahl der tatsächlichen Fälle an.

Was bedeuten diese Summen?

• Die Summe der ersten Zeile (460) zeigt die Gesamtzahl der vorhergesagten Betrugsfälle (TP + FP).
• Die Summe der zweiten Zeile (9.540) zeigt die Gesamtzahl der vorhergesagten echten Fälle (FN + TN).
• Die Summe der ersten Spalte (200) zeigt die Gesamtzahl der echten Betrugsfälle (TP + FN).
• Die Summe der zweiten Spalte (9.800) zeigt die Gesamtzahl der echten Fälle (FP + TN).
• Die Gesamtsumme (10.000) entspricht der Gesamtgröße unserer Stichprobe.

Was ist Präzision?

Die Präzisions -Messung sagt dir, wie gut deine positiven Vorhersagen sind. Es zeigt uns, wie viele Fälle, die als positiv vorhergesagt wurden, auch wirklich positiv waren. 

Ein genaues Modell heißt, dass es kaum Fehlalarme gibt. Wenn das Modell sagt, dass etwas stimmt, dann ist es wahrscheinlich auch so. Wenn zum Beispiel ein Online-Spiel jemanden wegen Betrugs sperrt, muss das echt sein. Zu viele ungerechtfertigte Sperren verärgern legitime Nutzer und führen zu schlechten Bewertungen. 

In der oben geprüften Terminologie ist die Präzision das Verhältnis von echten Positiven zu vorhergesagten Positiven.

Im obigen Beispiel ist die Genauigkeit 160/460, also ungefähr 34,8 %.

Was ist ein Rückruf?

Rückruf -Maßnahmen decken das ab. Es zeigt uns, wie viele der tatsächlichen positiven Ergebnisse als solche vorhergesagt wurden. Es ist das Verhältnis von echten positiven Ergebnissen zu allen tatsächlichen positiven Ergebnissen.

Denke bei der ersten Nachuntersuchung an Krebsdiagnosen. Ist es besser, lieber zu viel oder zu wenig zu diagnostizieren? Die meisten Leute würden dem ersten Punkt zustimmen. 

Bei einer Früherkennung kann es echt erschreckend sein, wenn man einen Fehlalarm bekommt. Aber es ist echt schlimm, wenn dir gesagt wird, du hättest keinen Krebs, obwohl du ihn tatsächlich hast, vor allem, weil du dadurch vielleicht eine Behandlung verpasst, die dein Leben retten könnte.

Im Beispiel oben ist die Erinnerung 160/200 oder 80 %.

Der Kompromiss zwischen Genauigkeit und Wiederauffindbarkeit

Es gibt ein Spannungsfeld zwischen Genauigkeit und Recall. Normalerweise wird die Genauigkeit besser, wenn die Präzision abnimmt, und umgekehrt.

Um zu verstehen, warum das so ist, schauen wir uns nochmal das Beispiel mit dem Betrug an. 

Die meisten Betrugsfälle wurden aufgedeckt, aber es gab auch viele falsche Alarme. Nehmen wir mal an, wegen Kundenbeschwerden hat die Geschäftsleitung beschlossen, die Entscheidungsschwelle von 0,7 auf 0,8 zu erhöhen. Damit eine Transaktion als Betrug markiert wird, muss sie jetzt mindestens 0,8 statt 0,7 Punkte haben.

Das hat das Modell konservativer gemacht. Es hat Betrug seltener vorhergesagt. Weniger Transaktionen wurden fälschlicherweise als Betrug gemeldet, aber dafür sind mehr echte Betrugsfälle durchgerutscht. Nachdem wir den Schwellenwert geändert hatten, ging die Anzahl der falschen Positiven von 300 auf 60 runter, aber die Anzahl der falschen Negativen stieg von 40 auf 80 hoch. 

Die Verwechslungsmatrix des neuen Modells sieht so aus:

Wie wir sehen können, waren 120 der 180 vorhergesagten Betrugsfälle tatsächlich betrügerisch, sodass die Genauigkeit von 34,8 % auf 66,7 % gestiegen ist. 

Der Preis für diese höhere Genauigkeit ist eine geringere Rückrufquote: 120 von 200 Betrugsfällen wurden als solche vorhergesagt, was bedeutet, dass die Genauigkeit von ursprünglich 80 % auf jetzt nur noch 60 % gesunken ist.

Das Modell findet jetzt insgesamt weniger Betrugsfälle, aber wenn es einen Betrug entdeckt, ist es viel sicherer. Das zeigt uns, wie wichtig es ist, beide Kennzahlen im Gleichgewicht zu halten, worauf wir später noch eingehen werden. 

Die Präzisions-Recall-Kurve

Um den Kompromiss zwischen Präzision und Recall zu zeigen, nutzen Datenwissenschaftler die Präzisions-Rückruf-Kurve (PR-Kurve). 

Dieses Diagramm zeigt die Präzision auf der y-Achse und die Wiederauffindbarkeit auf der x-Achse für jeden möglichen Entscheidungsschwellenwert (von 0 bis 1). Wenn du die Schwelle senkst, um mehr positive Fälle zu erfassen (Erhöhung der Wiederauffindungsrate), markierst du zwangsläufig mehr Fehlalarme (Verringerung der Genauigkeit). 

Das „perfekte“ Modell würde die obere rechte Ecke erreichen (100 % Präzision und Wiederauffindbarkeit), aber in Wirklichkeit musst du einen Punkt auf dieser Kurve wählen, der deinen spezifischen Geschäftsanforderungen entspricht.

In unserem Betrugsfallexempel haben wir ein Modell, das für jede Transaktion einen Betrugsscore ausgibt. Wenn die Punktzahl einer Transaktion mindestens den Schwellenwert erreicht, wird sie als Betrug markiert. Wenn wir die Schwelle senken, kriegen wir mehr vorhergesagte positive Ergebnisse, was normalerweise mehr echte positive Ergebnisse (höhere Recall-Rate) aber auch mehr Fehlalarme (niedrigere Präzisionsrate) mit sich bringt.

Mal sehen, wie das in der Praxis aussehen könnte. Angenommen, dein Unternehmen macht 10.000 Transaktionen pro Tag. Da die Betrugsrate auf 2 % geschätzt wird, rechnest du mit 200 betrügerischen Transaktionen pro Tag. Angenommen, das Betrugsbekämpfungsteam kann pro Tag 200 markierte Transaktionen (voraussichtlich positive Fälle) überprüfen.

Du schaust dir ein paar Schwellenwerte an und kommst zu diesen Ergebnissen:

• Bei einem Schwellenwert von 0,9 gibt's 100 vorhergesagte positive Fälle, mit einer Genauigkeit von 0,8 (80 echte Betrugsfälle, 20 Fehlalarme) und einer Wiederauffindungsrate von 0,4 (man entdeckt 80 von 200 Betrugsfällen). Du nutzt deine Kapazitäten nicht voll aus, weil du nur 100 pro Tag markierst, obwohl du 200 pro Tag überprüfen könntest. 
• Bei einem Schwellenwert von 0,5 gibt's 500 vorhergesagte positive Ergebnisse, mit einer Genauigkeit von 0,35 (175 echte Betrugsfälle, 325 Fehlalarme) und einer Wiederauffindungsrate von 0,875 (man entdeckt 175 von 200 Betrugsfällen). An dieser Stelle bist du überlastet, weil du 500 markierte Fälle nicht überprüfen kannst.
• Bei einem Schwellenwert von 0,7 gibt's 200 vorhergesagte positive Fälle, mit einer Genauigkeit von 0,6 (120 echte Betrugsfälle, 80 Fehlalarme) und einer Wiederauffindungsrate von 0,6 (man erwischt 120 von 200 Betrugsfällen). Das ist wahrscheinlich der Grenzwert, den du verwenden wirst, da du die volle Kapazität nutzen kannst und trotzdem einen recht ordentlichen Rückruf von 0,6 bekommst.

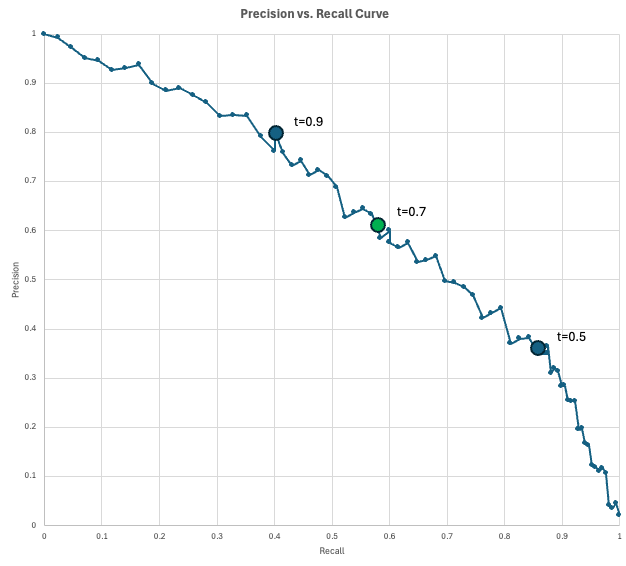
Die Kurve zeigt dir, welche Genauigkeit du bei einer bestimmten Rückrufquote bekommen kannst (oder umgekehrt).

Wann sollte man Präzision verwenden und wann nicht? Rückruf

Weil es bei Präzision und Recall immer ein Kompromiss ist, kommt es auf deinen konkreten Fall an, welche Metrik die richtige ist.

Wann man Präzision braucht

Es gibt eine umgekehrte Beziehung zwischen Genauigkeit und falschen Positiven. Deshalb ist ein genaues Modell eins, das richtig zwischen echten und falschen positiven Ergebnissen unterscheidet. Es ist echt zuverlässig.

Optimier die Genauigkeit, wenn die Kosten für ein falsches Positiv hoch sind. Beispiele für Fälle sind:

• Unumkehrbare Aktionen: Automatisierte Justiz- oder Account-Sperrsysteme. Jemanden zu beschuldigen, der unschuldig ist, oder das Konto von jemandem wegen eines Modellfehlers (False Positive) für immer zu löschen, kann echt schlimme Folgen haben.
• Teure Maßnahmen: Öl bohren oder eine Fabrik-Fließbandanlage abschalten. Wenn du auf eine positive Prognose reagierst und das Millionen kostet, musst du sicher sein, dass die Prognose stimmt, bevor du weitermachst.
• Spamfilterung: E-Mail-Postfächer. Es ist nervig, Spam-Mails zu bekommen (False Negative), aber es ist echt nicht okay, wenn ein wichtiges Jobangebot im Junk-Ordner landet (False Positive).

Wann man Recall benutzt

Genauso gibt's 'ne umgekehrte Beziehung zwischen Recall und False Negatives. Viele falsche Negative führen zu einer niedrigen Wiederauffindungsrate. Ein Modell mit hoher Wiederauffindbarkeit unterscheidet also richtig zwischen echten positiven und falschen negativen Ergebnissen. Es ist sicher.

Wenn es wichtiger ist, einen echten Fall nicht zu übersehen, als Fehlalarme in Kauf zu nehmen, solltest du die Recall-Metrik vor der Präzision priorisieren. Beispiele für Anwendungsfälle sind:

• Medizinische Sicherheit: Krankheitsscreening (z. B. Krebs oder Sepsis). Einen kranken Patienten zu übersehen, kann tödlich sein, während ein Fehlalarm zu weiteren Untersuchungen führt, was ein akzeptabler Preis ist.
• Cybersicherheit: Malware-Erkennung oder Netzwerk-Einbruch. Es ist besser, ein paar harmlose Anmeldungen als verdächtig zu markieren, als dass ein einzelner Hacker unbemerkt ins System eindringt.
• Fertigungsqualität: Fehlererkennung. Wenn du ein fehlerhaftes Produkt verschickst (falsch negatives Ergebnis), kann das Sicherheitsrisiken mit sich bringen und deinen Ruf ruinieren. Deshalb ist es besser, ein paar grenzwertige Artikel wegzuwerfen, als ein schlechtes Produkt durchgehen zu lassen.

F1-Score für die Balance zwischen Präzision und Recall

Wenn du dir nicht sicher bist, ob du ein Modell für Präzision oder Recall optimieren sollst, oder einfach beides berücksichtigen möchtest, kannst du den F1-Score zu Rate ziehen. 

Der F1-Score wird als harmonischer Mittelwert von Präzision und Recall definiert und kommt zum Einsatz, wenn du ein Gleichgewicht zwischen den beiden Metriken anstrebst. 

Wenn Präzision und Recall gleich sind, ist der F1-Score genau dieser Wert. Wenn einer der beiden Werte gegen Null geht, wird auch F1 ziemlich niedrig sein.

Im obigen Beispiel beträgt die Präzision 66,7 % und die Recall-Rate 60 %. Mit der oben genannten Formel kriegen wir einen F1-Score von ungefähr 63,2 %:

Die folgende Tabellezeigt, wie der F1-Score im Vergleich zu Genauigkeit, Präzision und Recall abschneidet.

Berechnung von Präzision und Recall in Python

Es gibt viele Möglichkeiten, Präzision, Recall und den F1-Score in Python zu berechnen. Im Folgenden zeige ich dir zwei Möglichkeiten: die Formeln direkt anwenden und spezielle Formeln aus dem Paket „ scikit-learn “ nutzen.

Berechnung von Präzision und Recall mit den Formeln

Wenn du die Zahlen der Verwechslungsmatrix kennst, kannst du die Metriken ganz einfach mit den oben angegebenen Formeln berechnen.

# Confusion matrix numbers
TP = 120
FP = 60
FN = 80
TN = 9740

# Formulas
precision = TP / (TP + FP)
recall = TP / (TP + FN)
f1 = 2 * precision * recall / (precision + recall)

# Output
print(f"{'Precision':<10} {precision:.1%}")
print(f"{'Recall':<10} {recall:.1%}")
print(f"{'F1':<10} {f1:.1%}")

Precision	66.7%
Recall		60.0%
F1		63.2%

Die Ausgabe dieses Codes stimmt mit unseren früheren Berechnungen überein.

Berechnung von Präzision und Recall mit scikit-learn

Du kannst auch die scikit-learn-Bibliothek lernen, um Metriken aus den Daten selbst zu berechnen. Im folgenden Beispiel simulieren wir y_true und y_predicted. Dann berechnen wir die Genauigkeit mit der Methode „ precision_score(y_true, y_false) “. Wir berechnen die Wiederauffindbarkeit und den F1-Score auf ähnliche Weise. Zum Schluss zeigen wir die Ergebnisse an.

import numpy as np
from sklearn.metrics import precision_score, recall_score, f1_score

# Simulate Data (y_true and y_pred)
TP, FP, FN, TN = 120, 60, 80, 9740
y_true = np.array(TP * [1] + FP * [0] + FN * [1] + TN * [0])
y_pred = np.array(TP * [1] + FP * [1] + FN * [0] + TN * [0])

# Compute metrics with scikit-learn
precision = precision_score(y_true, y_pred, zero_division=0)
recall = recall_score(y_true, y_pred, zero_division=0)
f1 = f1_score(y_true, y_pred, zero_division=0)

# Print aligned output using f-strings (no manual spaces, no colon)
print(f"{'Precision':<10} {precision:.1%}")
print(f"{'Recall':<10} {recall:.1%}")
print(f"{'F1':<10} {f1:.1%}")

Precision	66.7%
Recall		60.0%
F1		63.2%

Wie erwartet, passen diese Zahlen zu unseren früheren Berechnungen.

Fazit

Genauigkeit ist zwar ein guter Anfang, aber sie verdeckt oft die Details, die du brauchst, um zu verstehen, warum ein Modell nicht funktioniert. Präzision und Wiederauffindbarkeit geben dir ein klareres Bild, indem sie dich zwingen, den Kompromiss zwischen Fehlalarmen und verpassten Erkennungen zu betrachten. 

Letztendlich ist die Wahl der richtigen Metrik nicht nur ein mathematisches Problem, sondern eine praktische Entscheidung darüber, welche Art von Fehlern dein System sich leisten kann.

Bist du bereit, deine eigenen Modelle für maschinelles Lernen zu entwickeln? Fang mit den Grundlagen des maschinellen Lernens in Python Lernpfad heute!