Qu'est-ce qu'une matrice de confusion dans l'apprentissage automatique ? L'outil d'évaluation des modèles expliqué

Cette année a été marquée par l'innovation dans le domaine de la science des données, l'intelligence artificielle et l'apprentissage automatique faisant la une des journaux. Si les progrès réalisés en 2023 ne font aucun doute, il est important de reconnaître que nombre de ces avancées en matière d'apprentissage automatique n'ont été possibles que grâce aux processus d'évaluation corrects auxquels les modèles sont soumis. Les spécialistes des données sont chargés de veiller à ce que des évaluations et des processus précis soient mis en place pour mesurer les performances d'un modèle d'apprentissage automatique. Il ne s'agit pas d'un avantage, mais d'une nécessité.

Si vous souhaitez vous initier à la science des données, cet article vous guidera à travers les étapes cruciales de l'évaluation des modèles à l'aide de la matrice de confusion, un outil relativement simple mais puissant, largement utilisé dans l'évaluation des modèles.

Nous allons donc nous plonger dans le vif du sujet et en apprendre davantage sur la matrice de confusion.

Qu'est-ce que la matrice de confusion ?

La matrice de confusion est un outil utilisé pour évaluer la performance d'un modèle et est représentée visuellement sous la forme d'un tableau. Il permet aux praticiens des données de mieux comprendre les performances, les erreurs et les faiblesses du modèle. Cela permet aux praticiens des données d'analyser plus en détail leur modèle en l'affinant.

La structure de la matrice de confusion

Découvrons la structure de base d'une matrice de confusion, en prenant l'exemple de l'identification d'un courriel comme étant du spam ou non.

• Vrai positif (TP) - Votre modèle a prédit la classe positive. Par exemple, identifier un courriel de spam comme étant du spam.
• Vrai négatif (TN) - Votre modèle a correctement prédit la classe négative. Par exemple, identifier un courriel normal comme n'étant pas du spam.
• Faux positif (FP) - Votre modèle a mal prédit la classe positive. Par exemple, l'identification d'un courriel normal comme étant du spam.
• Faux négatif (FN) - Votre modèle a mal prédit la classe négative. Par exemple, identifier un courriel de spam comme un courriel normal.

Pour bien comprendre le concept de matrice de confusion, jetez un coup d'œil à la visualisation ci-dessous :

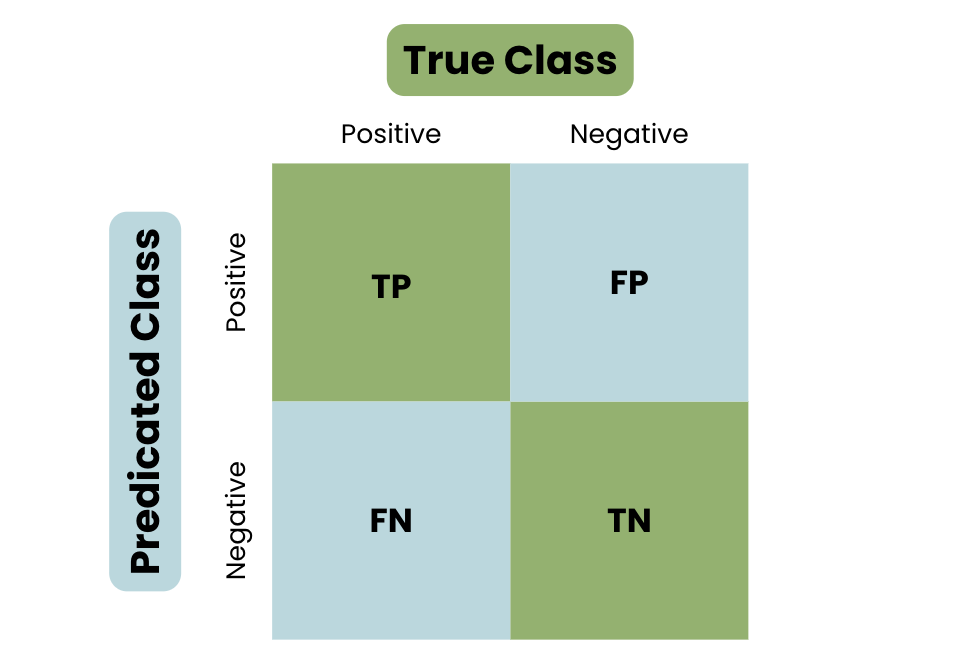
La structure de base d'une matrice de confusion

Terminologie de la matrice de confusion

Pour bien comprendre la matrice de confusion, il est essentiel de connaître les paramètres importants utilisés pour mesurer la performance d'un modèle.

Définissons les paramètres importants :

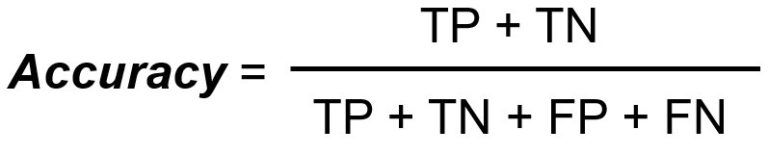
Précision

La précision mesure le nombre total de classifications correctes divisé par le nombre total de cas.

Rappel/sensibilité

Le rapport rappel/sensibilité mesure le nombre total de vrais positifs divisé par le nombre total de vrais positifs.

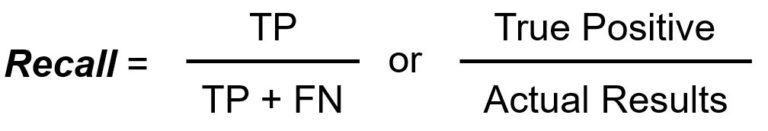
Précision

La précision mesure le nombre total de vrais positifs divisé par le nombre total de positifs prédits.

Spécificité

La spécificité mesure le nombre total de vrais négatifs divisé par le nombre total de vrais négatifs.

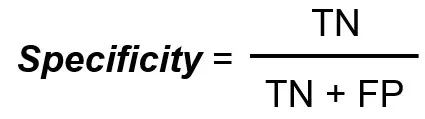
Score F1

Le score F1 est une mesure unique qui est une moyenne harmonique de la précision et du rappel.

Le rôle d'une matrice de confusion

Pour mieux comprendre la matrice de confusion, il faut en comprendre l'objectif et savoir pourquoi elle est largement utilisée.

Lorsqu'il s'agit de mesurer les performances d'un modèle ou quoi que ce soit d'autre en général, les gens se concentrent sur la précision. Cependant, le fait de s'appuyer fortement sur la mesure de la précision peut conduire à des décisions erronées. Pour comprendre cela, nous allons examiner les limites de l'utilisation de la précision en tant que mesure autonome.

Limites de la précision en tant que mesure autonome

Comme défini ci-dessus, la précision mesure le nombre total de classifications correctes divisé par le nombre total de cas. Cependant, l'utilisation de cette mesure en tant que telle comporte des limites :

• Travailler avec des données déséquilibrées: Aucune donnée n'est jamais parfaite, et l'utilisation de la mesure de la précision doit être évaluée en fonction de son pouvoir prédictif. Par exemple, si vous travaillez avec un ensemble de données où une classe l'emporte sur une autre, le modèle atteindra un taux de précision plus élevé car il prédira la classe majoritaire.
• Types d'erreurs: Comprendre et connaître les performances de votre modèle dans un contexte spécifique vous aidera à l'affiner et à l'améliorer. Par exemple, la différenciation des types d'erreurs au moyen d'une matrice de confusion, telle que FP et FN, vous permettra d'explorer les limites du modèle.

Malgré ces limites, la matrice de confusion, ainsi que la variété des mesures, offre un aperçu plus détaillé de la manière d'améliorer la performance d'un modèle.

Les avantages d'une matrice de confusion

Comme le montre la structure de base d'une matrice de confusion, les prédictions sont réparties en quatre catégories : Vrai positif, Vrai négatif, Faux positif et Faux négatif.

Cette analyse détaillée offre des informations précieuses et des solutions pour améliorer les performances d'un modèle :

• Résoudre les données déséquilibrées: Comme nous l'avons vu, l'utilisation de la précision en tant que mesure autonome présente des limites lorsqu'il s'agit de données déséquilibrées. L'utilisation d'autres mesures, telles que la précision et le rappel, permet d'obtenir une vision plus équilibrée et une représentation plus précise. Par exemple, les faux positifs et les faux négatifs peuvent avoir de lourdes conséquences dans des secteurs tels que la finance.
• Différentiateur de type d'erreur: La compréhension des différents types d'erreurs produites par le modèle d'apprentissage automatique permet de connaître ses limites et les domaines à améliorer.
• Compromis: Le compromis entre l'utilisation de différentes mesures dans une matrice de confusion est essentiel car elles ont un impact l'une sur l'autre. Par exemple, une augmentation de la précision entraîne généralement une diminution du rappel. Cela vous aidera à améliorer la performance du modèle en utilisant les connaissances des valeurs métriques impactées.

Calcul d'une matrice de confusion

Maintenant que nous avons une bonne compréhension d'une matrice de confusion de base, de sa terminologie et de son utilisation, passons au calcul manuel d'une matrice de confusion, suivi d'un exemple pratique.

Calcul manuel d'une matrice de confusion

Voici un guide étape par étape sur la manière de calculer manuellement une matrice de confusion.

Définir les résultats

La première étape consistera à identifier les deux résultats possibles de votre tâche : Positif ou négatif.

Collecte des prévisions

Une fois les résultats possibles définis, l'étape suivante consiste à collecter toutes les prédictions du modèle, y compris le nombre de fois où le modèle a prédit chaque classe et son occurrence.

Classification des résultats

Une fois que toutes les prédictions ont été rassemblées, l'étape suivante consiste à classer les résultats dans les quatre catégories :

• Vrai positif (TP)
• Vrai négatif (TN)
• Faux positif (FP)
• Faux négatif (FN)

Créer une matrice

Une fois les résultats classés, l'étape suivante consiste à les présenter dans un tableau matriciel, en vue d'une analyse plus approfondie à l'aide de divers paramètres.

Exemple pratique de matrice de confusion

Prenons un exemple pratique pour illustrer ce processus.

En continuant à utiliser le même exemple d'identification d'un courriel comme étant du spam ou non, créons un ensemble de données hypothétique où le spam est positif et le non spam est négatif. Nous disposons des données suivantes :

• Parmi les 200 courriels, 80 sont en fait des spams, dont 60 sont correctement identifiés par le modèle (TP).
• Parmi les 200 courriels, 120 ne sont pas des spams, dont 100 sont correctement identifiés par le modèle comme n'étant pas des spams (TN).
• Parmi les 200 courriels, le modèle identifie à tort 20 courriels non spammés comme étant des spams (FP).
• Parmi les 200 courriels, le modèle ne détecte pas 20 courriels de spam et les identifie comme des courriels non spam (FN).

À ce stade, nous avons défini les résultats et collecté les données ; l'étape suivante consiste à classer les résultats dans les quatre catégories :

• Vrai positif : 60
• Vrai négatif : 100
• Faux positif : 20
• Faux négatif : 20

L'étape suivante consiste à transformer cette matrice en matrice de confusion :

Que nous apprend donc la matrice de confusion ?

• Les Vrais Positifs et les Vrais Négatifs indiquent que les prédictions sont exactes.
• Les faux positifs indiquent que le modèle a mal prédit la classe positive.
• Les faux négatifs indiquent que le modèle n'a pas réussi à identifier et à prédire la classe positive.

En utilisant cette matrice de confusion, nous pouvons calculer les différentes mesures : Précision, rappel/sensibilité, exactitude, spécificité et score F1.

Résultats de la matrice de confusion

Précision vs. Rappel

Vous vous demandez peut-être pourquoi le score F1 inclut la précision et le rappel dans sa formule. La mesure du score F1 est cruciale lorsque vous traitez des données déséquilibrées ou lorsque vous souhaitez équilibrer le compromis entre la précision et le rappel.

La précision mesure l'exactitude d'une prédiction positive. Il répond à la question suivante : "lorsque le modèle prédit VRAI, combien de fois a-t-il eu raison ? La précision, en particulier, est importante lorsque le coût d'un faux positif est élevé.

Le rappel ou la sensibilité mesure le nombre de positifs réels correctement identifiés par le modèle. Il répond à la question suivante : "Lorsque la classe est VRAIE, combien de fois le classificateur s'est-il trompé ?

Le rappel est important lorsqu'il est démontré que le fait de manquer une instance positive (FN) est nettement plus grave que le fait d'étiqueter incorrectement des instances négatives comme positives.

• Utilisation de précision: Les faux positifs peuvent avoir de graves conséquences. Par exemple, un modèle de classification utilisé dans le secteur financier a identifié à tort une transaction comme frauduleuse. Dans de tels scénarios, la mesure de la précision est importante.
• Rappeler l'utilisation: Il peut être impératif d'identifier tous les cas positifs. Par exemple, les modèles de classification utilisés dans le domaine médical qui ne parviennent pas à poser un diagnostic correct peuvent être préjudiciables. Dans les scénarios où il est essentiel d'identifier correctement tous les cas positifs, la mesure de rappel est importante.

Matrice de confusion en utilisant Scikit-learn en Python

Pour mettre cela en perspective, créons une matrice de confusion à l'aide de Scikit-learn en Python, en utilisant un classificateur Random Forest.

La première étape consistera à importer les bibliothèques requises et à construire votre ensemble de données synthétiques.

# Import Libraries
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns

# Synthetic Dataset
X, y = make_classification(n_samples=1000, n_features=20,
                           n_classes=2, random_state=42)

# Split into Training and Test Sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

L'étape suivante consiste à entraîner le modèle à l'aide d'une simple forêt aléatoire.

# Train the Model
model = RandomForestClassifier(random_state=42)
model.fit(X_train, y_train)

Comme nous l'avons fait dans l'exemple pratique, nous devrons classer les résultats et les transformer en une matrice de confusion. Pour ce faire, nous commençons par prédire sur les données de test, puis nous générons une matrice de confusion :

# Predict on the Test Data
y_pred = model.predict(X_test)

# Generate the confusion matrix
cm = confusion_matrix(y_test, y_pred)

Nous voulons maintenant générer une représentation visuelle de la matrice de confusion :

# Create a Confusion Matrix
plt.figure(figsize=(8, 8))
sns.heatmap(cm, annot=True, fmt='d', cmap='Greens')
plt.title('Confusion Matrix')
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()

Voici le résultat :

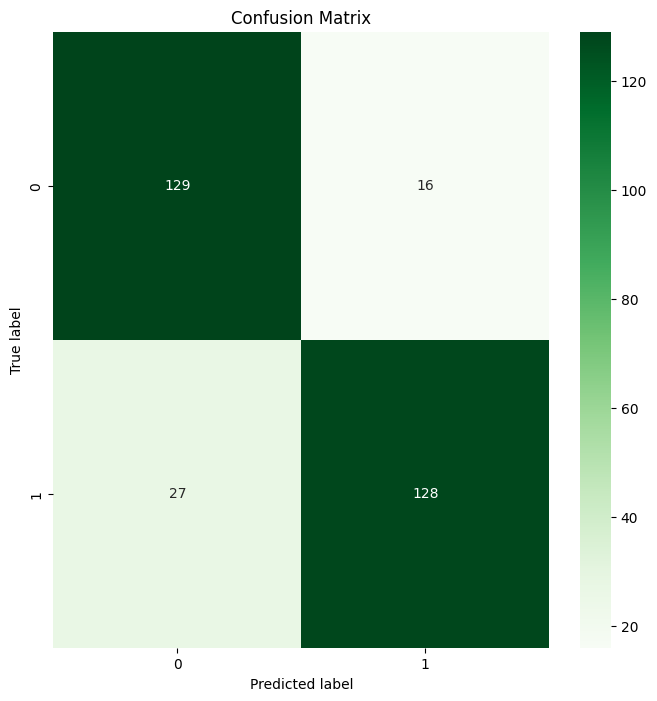
Matrice de confusion de Random Forest Sortie

Tada 🎉 Vous avez réussi à créer votre première matrice de confusion en utilisant Scikit-learn !

Conclusion

Dans cet article, nous avons exploré la définition d'une matrice de confusion, la terminologie importante entourant l'outil d'évaluation, ainsi que les limites et l'importance des différentes métriques. Pouvoir calculer manuellement une matrice de confusion est important pour votre base de connaissances en science des données, de même que pouvoir l'exécuter à l'aide de bibliothèques telles que Scikit-learn.

Si vous souhaitez approfondir votre connaissance des matrices de confusion, vous pouvez vous exercer à l'utilisation des matrices de confusion en R avec Understanding Confusion Matrix in R. Plongez un peu plus profondément avec notre cours Validation de modèle en Python, où vous apprendrez les bases de la validation de modèle, les techniques de validation et commencerez à créer des modèles validés et performants.