Tutoriel Python sur le tri par fusion

Le tri des données est l'une des opérations les plus courantes que les spécialistes des données effectuent dans leur travail quotidien. Nous avons souvent besoin d'afficher des données dans un certain ordre pour en extraire des informations significatives. Heureusement, de nos jours, il n'est plus nécessaire d'effectuer cette tâche manuellement. Les ordinateurs peuvent faire la magie à notre place avec des performances imbattables.

Il existe plusieurs stratégies pour trier les données. Dans ce tutoriel, nous analyserons l'une des techniques de tri les plus efficaces. L'algorithme "merge sort" utilise une stratégie de division et de conquête pour trier un tableau non trié en le divisant d'abord en tableaux plus petits, qui sont ensuite fusionnés dans le bon ordre. 

Dans les prochaines sections, nous aborderons tous les détails de l'algorithme de tri par fusion, son apparence en Python et quelques conseils pratiques pour une mise en œuvre sans heurts.

Qu'est-ce que le tri par fusion ?

Il existe de nombreux algorithmes de tri, mais il est difficile d'en trouver un qui soit plus performant que le tri par fusion. Sans surprise, cet algorithme est utilisé dans toutes sortes d'applications réelles, comme le tri de grandes bases de données ou l'organisation de fichiers sur un ordinateur ordinaire.

L'algorithme est basé sur le paradigme "diviser pour régner", qui peut être décomposé en trois parties :

• Diviser: ce processus divise le problème en sous-problèmes plus petits. 
• Conquérir: les sous-problèmes sont résolus de manière récursive. 
• Combiner: les solutions des sous-problèmes sont combinées pour obtenir la solution finale.

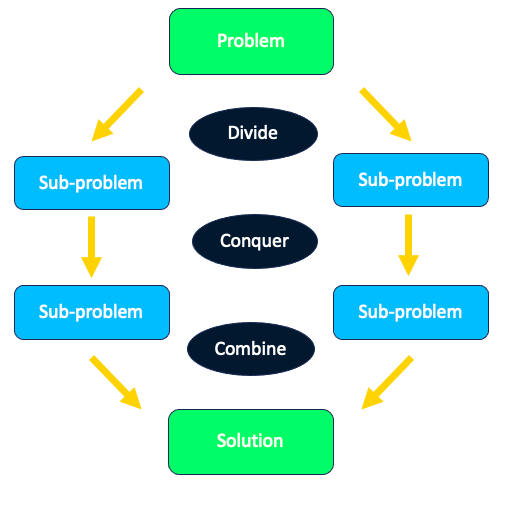
Stratégie de division et de conquête

Voyons comment fonctionne le tri par fusion. Supposons que nous voulions ordonner les nombres suivants en appliquant l'algorithme de tri par fusion. L'algorithme divise les données de manière récursive en deux parties et continue à les diviser jusqu'à ce que chaque liste ne contienne qu'un seul élément. Ensuite, nous les combinons en les triant dans une autre liste.

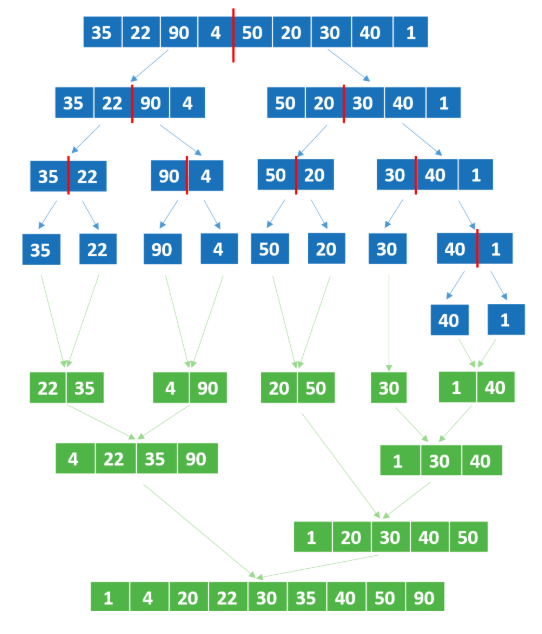
Problème de tri de fusion. Source : DataCamp

Complexité temporelle et spatiale du tri par fusion

Il est impossible de savoir à l'avance quel est l'algorithme de tri qui fonctionne le mieux pour un problème donné. Au-delà de l'algorithme, plusieurs variables doivent être prises en compte, notamment le langage de programmation utilisé pour écrire le code, le matériel dans lequel il est exécuté et les particularités des données à trier. 

Bien qu'il soit impossible de prédire la durée d'exécution exacte d'un algorithme de tri, nous pouvons néanmoins comparer les performances de divers algorithmes de tri en analysant la complexité en termes de temps et d'espace.

Complexité temporelle du tri par fusion

Comme nous l'avons expliqué dans un autre guide sur la notation Big O et la complexité temporelle, l'objectif de l'analyse de la complexité temporelle n'est pas de prédire la durée d'exécution exacte d'un algorithme, mais plutôt d'évaluer l'efficacité d'un algorithme en analysant l'évolution de sa durée d'exécution à mesure que la quantité de données d'entrée augmente.

L'analyse de la complexité temporelle est écrite en notation Big O, une notation mathématique qui décrit la vitesse à laquelle une fonction croît ou décroît. Le tri par fusion a une complexité temporelle log-linéaire ou linéaire, notée O(N log(N)), où N est le nombre d'éléments de la liste. La lettre "O" représente l'"ordre" de croissance. 

Dans l'analyse de la complexité temporelle, la complexité linéaireithmique se comporte à peu près de la même manière que la complexité linéaire, ce qui signifie que son exécution sera directement proportionnelle à la quantité de données. Ainsi, si la quantité de données est doublée, le temps nécessaire à l'algorithme pour traiter les données devrait également doubler, c'est-à-dire que le nombre de divisions et de fusions sera doublé.

Comme la complexité temporelle du tri par fusion se comporte de manière linéaire, sa complexité reste la même dans le meilleur, le moyen et le pire des cas. Cela signifie que, quel que soit l'ordre des entrées, l'algorithme prendra toujours le même nombre d'étapes.

Complexité spatiale du tri par fusion

Enfin, outre le temps nécessaire pour terminer la tâche, un autre aspect important de l'analyse de la complexité d'un algorithme est l'estimation de la quantité de mémoire dont l'algorithme aura besoin au fur et à mesure que le problème prendra de l'ampleur. 

Ceci est couvert par les concepts de complexité de l'espace et d'espace auxiliaire. Ce dernier fait référence à l'espace supplémentaire ou temporaire utilisé par un algorithme, tandis que le premier fait référence à l'espace total pris par l'algorithme par rapport à la taille de l'entrée. En d'autres termes, la complexité de l'espace comprend à la fois l'espace auxiliaire et l'espace utilisé par l'entrée.

Le tri par fusion a une complexité spatiale de O(N). En effet, il utilise un tableau auxiliaire de taille N pour fusionner les moitiés triées du tableau d'entrée. Le tableau auxiliaire est utilisé pour stocker le résultat fusionné, et le tableau d'entrée est remplacé par le résultat trié.

Implémentation du tri par fusion en Python

Mettons en œuvre l'algorithme de tri par fusion en Python. Il existe plusieurs façons de coder l'algorithme, mais nous nous en tiendrons à celle basée sur la récursivité, qui est sans doute la plus facile à comprendre et qui nécessite moins de lignes de code que les autres alternatives basées sur l'itération.

Comprendre la récursivité dans le tri par fusion

Si vous êtes novice en la matière, sachez qu'en programmation, la récursivité se produit lorsqu'une fonction s'appelle elle-même. Vous pouvez consulter notre tutoriel Comprendre les fonctions récursives en Python pour tout savoir sur ces puissantes fonctions.

Pour mettre en œuvre le tri par fusion, nous définissons d'abord le cas de base: si la liste n'a qu'un seul élément, elle est déjà triée, et nous retournons donc immédiatement. Sinon, nous divisons la liste en deux moitiés, left_half et right_half, et appelons merge_sort() récursivement sur chacune d'entre elles. Ce processus se poursuit jusqu'à ce que toutes les sous-listes contiennent un seul élément.

Une fois ces sous-listes triées, nous entamons le processus de fusion. Pour ce faire, nous initialisons trois variables d'index : i pour le cursus de la position dans left_half, j pour right_half, et k pour la liste fusionnée finale. Nous comparons ensuite les éléments des deux moitiés. Si l'élément actuel de left_half est plus petit, nous le plaçons dans my_list[k] et faisons avancer i. Sinon, nous prenons l'élément de right_half, nous le plaçons dans my_list[k] et nous incrémentons j. Après chaque comparaison, nous faisons passer k à la position suivante dans la liste finale.

Ce processus se poursuit jusqu'à ce que nous ayons comparé tous les éléments de l'une des moitiés. S'il reste des éléments dans left_half ou right_half, nous les ajoutons directement à la liste finale, en veillant à ce qu'aucune donnée ne soit oubliée. Comme le tri par fusion fonctionne de manière récursive, ce processus de fusion est exécuté à chaque niveau de récursivité jusqu'à ce que la liste entière soit triée.

Mise en œuvre de Python

Vous trouverez ci-dessous le code utilisant comme exemple la liste non triée du diagramme précédent :

def merge_sort(my_list):
    if len(my_list) > 1: 
        mid = len(my_list)//2
        left_half = my_list[:mid]
        right_half = my_list[mid:]
       
        merge_sort(left_half)
        merge_sort(right_half)

        i = j = k = 0
 
        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                my_list[k] = left_half[i]                
                i += 1
            else:
                my_list[k] = right_half[j]
                j += 1
            k += 1
     
        while i < len(left_half):
            my_list[k] = left_half[i]
            i += 1
            k += 1
 
        while j < len(right_half):
            my_list[k] = right_half[j]
            j += 1
            k += 1

my_list = [35,22,90,4,50,20,30,40,1]
merge_sort(my_list)
print(my_list)
>>> [1, 4, 20, 22, 30, 35, 40, 50, 90]

Tri par fusion et autres algorithmes de tri

Le tri par fusion est un algorithme de tri assez rapide, particulièrement adapté aux grandes bases de données, et il est souvent utilisé comme référence pour d'autres algorithmes. Toutefois, lorsqu'il s'agit de listes plus courtes, ses performances tendent à être inférieures à celles des autres algorithmes de tri.

Dans le tableau suivant, vous trouverez une comparaison du tri par fusion avec d'autres algorithmes de tri populaires.

Applications pratiques du tri par fusion

Le tri par fusion est très performant lorsqu'il s'agit de trier de grandes listes, mais son efficacité diminue lorsqu'il s'agit de petites listes. De même, il tend à être moins efficace dans les scénarios où il existe déjà un certain degré ou ordre dans les listes d'entrée, car le tri par fusion effectue les mêmes étapes quel que soit l'ordre de la liste.

Les listes chaînées constituent un cas d'utilisation idéal où le tri par fusion s'avère particulièrement pratique. Une liste chaînée est une structure de données qui comprend une connexion de nœuds linéairement liés les uns aux autres. Chaque nœud contient les données et le lien qui le relie au nœud suivant.

Le tri par fusion est préféré pour les listes chaînées car il ne nécessite qu'un accès séquentiel aux données, ce qui correspond bien à la nature des listes chaînées. En outre, le tri par fusion est un algorithme de tri stable (c'est-à-dire qu'il préserve l'ordre relatif des éléments égaux dans la sortie triée), ce qui est très important pour maintenir l'ordre des listes chaînées.

Erreurs courantes et dépannage

L'algorithme de tri par fusion est assez simple et les possibilités d'amélioration du code sont limitées. Toutefois, vous pouvez accroître la complexité de votre stratégie de tri en tenant compte de la taille des données d'entrée. 

Nous avons déjà établi que le tri par fusion fonctionne mieux avec les grands ensembles de données. Pour les ensembles de données plus petits, d'autres algorithmes de tri ayant une complexité temporelle de O(N^2), comme le tri par insertion, donnent de meilleurs résultats. Dans ce cas, il vous suffit de créer un seuil de taille en dessous duquel vous utiliserez l'algorithme de tri par insertion au lieu de l'algorithme de fusion et de tri.

À part cela, une bonne idée à explorer serait la parallélisation. Les étapes du tri par fusion peuvent être facilement parallélisées avec la puissance de calcul adéquate, ce qui permet de réduire le temps d'exécution. Lisez notre guide CPU vs GPU pour en savoir plus sur l'informatique parallèle. 

Conclusion

Le tri par fusion est l'un des algorithmes de tri les plus efficaces et les plus populaires, mais il y a bien d'autres choses à apprendre dans l'univers merveilleux et toujours en expansion des algorithmes. Si vous vous intéressez aux aspects techniques des algorithmes, à leur fonctionnement et à la complexité, aux vertus et aux inconvénients qui leur sont associés, ces ressources de DataCamp peuvent vous aider à poursuivre votre apprentissage :

• Cours d'introduction aux structures de données et aux algorithmes 
• Le cursus de compétences en programmation Python
• Le cursus des fondamentaux des données en Python
• Cours intermédiaire de Python
• Analyste de données en Python Curriculum vitae 
• Notation Big O et complexité temporelle