Python Merge Sort Tutorial

Sorting data is one of the most common operations data practitioners do in their daily work. Many times we need to display data in a certain order to extract meaningful information. Luckily, nowadays we don’t have to do this task manually. Computers can do the magic for us with unbeatable performance.

There are several strategies to sort data. In this tutorial, we will analyze one of the most effective sorting techniques. The “merge sort” algorithm uses a divide-and-conquer strategy to sort an unsorted array by first breaking it into smaller arrays, which are lately merged in the right order. 

In the coming sections, we will discuss all the details of the merge sort algorithm, how it looks in Python, and some practical tips for smooth implementation.

What is Merge Sort?

There are many sorting algorithms out there, but it’s difficult to find one that performs better than merge sort. Unsurprisingly, this algorithm is used in all kinds of real-world applications, like sorting large databases or organizing files on a regular computer.

The algorithm is based on the divide-and-conquer paradigm, which can be broken down into three parts:

• Divide: this process divides the problem into smaller sub-problems. 
• Conquer: the sub-problems are solved recursively. 
• Combine: the solutions of the sub-problems are combined in order to achieve the final solution.

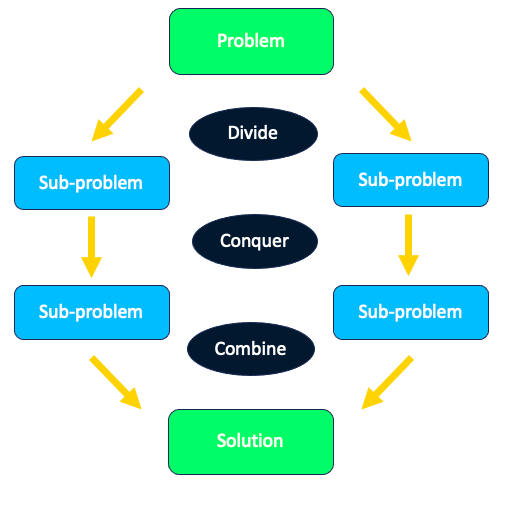
Divide and conquer strategy

Let's see how merge sort works. Suppose we want to order the following numbers by applying the merge sort algorithm. The algorithm divides the data recursively into two parts and keeps dividing until each list has one element. Then, we combine them by sorting them into another list.

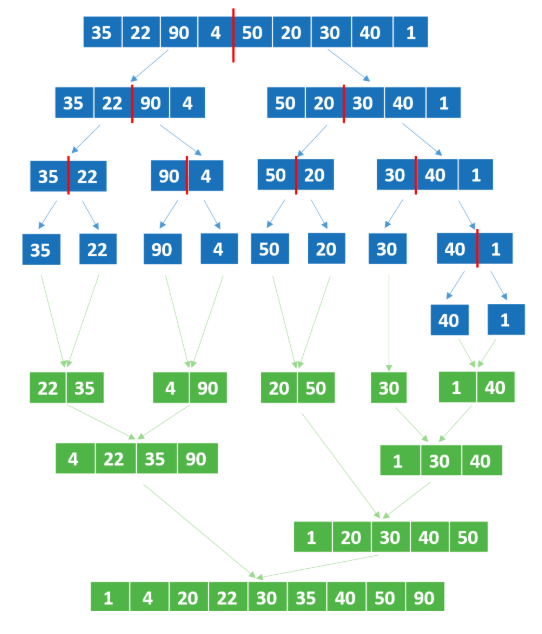
Merge Sort Problem. Source: DataCamp

Time and Space Complexity of Merge Sort

It’s impossible to know in advance what is the sorting algorithm that works best for a certain problem. Several variables need to be considered beyond the algorithm, including the programming language used to write the code, the hardware in which they’re executed, and the particularities of the data to be sorted. 

Although we can’t predict the exact runtime of a sorting algorithm, we can still compare the performance of various sorting algorithms by analyzing time and space complexity.

Time complexity of merge sort

As we explained in a separate guide on Big O Notation and Time Complexity, the goal of time complexity analysis isn’t to predict the exact runtime of an algorithm but rather to evaluate how efficient an algorithm is by analyzing how its running time changes as the amount of input data increases.

Time complexity analysis is written in Big O notation, a mathematical notation that describes the rate at which a function grows or declines. The merge sort has log-linear or linearithmic time complexity, noted as O(N log(N)), where N is the number of elements in the list. The letter 'O' stands for the 'order' of growth. 

In time complexity analysis, linearithmic complexity behaves approximately similarly to linear complexity, meaning its execution will be directly proportional to the amount of data. Thus, if the amount of data is doubled, the time it takes for the algorithm to process the data should also double, i.e., the number of divisions and merges will double.

Because the time complexity of merge sort behaves linearly, its complexity remains the same for the best, average, and worst cases. That means that, regardless of the input order, the algorithm will always take the same number of steps to complete.

Space complexity of merge sort

Finally, in addition to the time required to finish the task, another important aspect when analyzing algorithm complexity is estimating how much memory the algorithm will require to complete as the problem becomes bigger. 

This is covered by the concepts of space complexity and auxiliary space. The latter refers to the extra space or temporary space used by an algorithm, whereas the former refers to the total space taken by the algorithm with respect to the input size. In other words, space complexity includes both auxiliary space and space used by input.

Merge sort has a space complexity of O(N). This is because it uses an auxiliary array of size N to merge the sorted halves of the input array. The auxiliary array is used to store the merged result, and the input array is overwritten with the sorted result.

Merge Sort Implementation in Python

Let's implement the merge sort algorithm in Python. There are several ways to code the algorithm; however, we will stick to the one based on recursion, which is arguably the easiest to understand and requires fewer lines of code than other alternatives based on iteration.

Understanding recursion in merge sort

If you’re new to the topic, in programming, recursion happens when a function calls itself. You can check out our Understanding Recursive Functions in Python Tutorial to learn all about these powerful functions.

To implement merge sort, we first define the base case: if the list has only one element, it is already sorted, so we return immediately. Otherwise, we split the list into two halves, left_half and right_half, and call merge_sort() recursively on each of them. This process continues until all sublists contain a single element.

Once we have these sorted sublists, we begin the merging process. To do this, we initialize three index variables: i for tracking the position in left_half, j for right_half, and k for the final merged list. We then compare elements from both halves. If the current element in left_half is smaller, we place it in my_list[k] and move i forward. Otherwise, we take the element from right_half, place it in my_list[k], and increment j. After each comparison, we move k forward to the next position in the final list.

This process continues until we have compared all elements in one of the halves. If any elements remain in either left_half or right_half, we append them directly to the final list, ensuring that no data is left behind. Because merge sort operates recursively, this merging process is executed at every level of recursion until the entire list is sorted.

Python implementation

Below, you can find the code using the unsorted list of the previous diagram as an example:

def merge_sort(my_list):
    if len(my_list) > 1: 
        mid = len(my_list)//2
        left_half = my_list[:mid]
        right_half = my_list[mid:]
       
        merge_sort(left_half)
        merge_sort(right_half)

        i = j = k = 0
 
        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                my_list[k] = left_half[i]                
                i += 1
            else:
                my_list[k] = right_half[j]
                j += 1
            k += 1
     
        while i < len(left_half):
            my_list[k] = left_half[i]
            i += 1
            k += 1
 
        while j < len(right_half):
            my_list[k] = right_half[j]
            j += 1
            k += 1

my_list = [35,22,90,4,50,20,30,40,1]
merge_sort(my_list)
print(my_list)
>>> [1, 4, 20, 22, 30, 35, 40, 50, 90]

Merge Sort vs Other Sorting Algorithms

Merge sort is a quite fast sorting algorithm, especially well-suited for large databases, and it’s often used as a benchmark for other algorithms. However, when it comes to shorter lists, its performance tends to be lower than other sorting algorithms.

In the following table, you can find a comparison of merge sort with other popular sorting algorithms.

Practical Applications of Merge Sort

Merge sort has a high performance when sorting large lists, but its efficiency decreases when working with smaller lists. Equally, it tends to be less efficient in scenarios where there is already some degree or order in the input lists, as merge sort will perform the same steps no matter the order of the list.

A great use case where merge sort comes particularly handy is linked lists. A linked list is a data structure that comprises a connection of nodes linearly linked to each other. Each node contains the data and the link to connect it with the next node.

Merge sort is preferred for linked lists because it only requires sequential access to data, which aligns well with the nature of linked lists. Also, merge sort is a stable sorting algorithm (i.e. it preserves the relative order of equal elements in the sorted output), which is a very important consideration in maintaining the order of linked lists.

Common Errors and Troubleshooting

The merge sort algorithm is pretty straightforward, and the room for improvement in the code is limited. However, you can increase the complexity of your sorting strategy by taking into account the size of the input data. 

We’ve already established that merge sort works better with larger datasets. For smaller datasets, other sorting algorithms with O(N^2) time complexity, like insertion sort, make work better. In this case, you just would need to create a size threshold below which you would go for the insertion sort algorithm instead of merge and sort.

Other than that, a good idea to explore would be parallelization. The steps of merge sort can be easily parallelized with the right computing power, thereby reducing the time to complete. Read our CPU vs GPU guide to learn more about parallel computing. 

Conclusion

Merge sort is one of the most effective and popular sorting algorithms out there, but there is much more to learn in the wonderful and ever-expanding universe of algorithms. If you are interested in the technicalities of algorithms, how they work, and their associated complexity, virtues, and drawbacks, these DataCamp resources can help you continue your learning:

• Introduction to Data Structures and Algorithms Course 
• Python Programming Skill Track
• Python Data Fundamentals Skill Track
• Intermediate Python Course
• Data Analyst in Python Career Track 
• Big O Notation and Time Complexity