Python Merge Sort Tutorial

Das Sortieren von Daten ist eine der häufigsten Tätigkeiten, die Datenpraktiker/innen bei ihrer täglichen Arbeit ausführen. Oftmals müssen wir Daten in einer bestimmten Reihenfolge anzeigen, um aussagekräftige Informationen zu erhalten. Zum Glück müssen wir diese Aufgabe heutzutage nicht mehr manuell erledigen. Computer können mit unschlagbarer Leistung für uns zaubern.

Es gibt verschiedene Strategien, um Daten zu sortieren. In diesem Lernprogramm werden wir eine der effektivsten Sortiertechniken analysieren. Der "Merge Sort"-Algorithmus verwendet eine Divide-and-Conquer-Strategie, um ein unsortiertes Array zu sortieren, indem er es zunächst in kleinere Arrays aufteilt, die dann in der richtigen Reihenfolge zusammengeführt werden. 

In den nächsten Abschnitten werden wir alle Details des Merge-Sortieralgorithmus besprechen, wie er in Python aussieht und einige praktische Tipps für eine reibungslose Implementierung geben.

Was ist Merge Sort?

Es gibt viele Sortieralgorithmen, aber es ist schwierig, einen zu finden, der besser ist als Merge Sort. Es überrascht nicht, dass dieser Algorithmus in allen möglichen realen Anwendungen eingesetzt wird, z. B. beim Sortieren großer Datenbanken oder beim Organisieren von Dateien auf einem normalen Computer.

Der Algorithmus basiert auf dem Divide-and-Conquer-Paradigma, das in drei Teile unterteilt werden kann:

• Aufteilen: Bei diesem Verfahren wird das Problem in kleinere Teilprobleme aufgeteilt. 
• Bezwingen: Die Teilprobleme werden rekursiv gelöst. 
• Kombinieren: Die Lösungen der Teilprobleme werden kombiniert, um die endgültige Lösung zu erhalten.

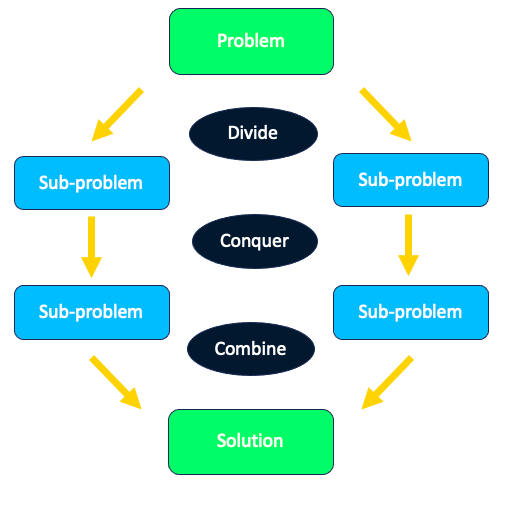
Strategie des Teilens und Eroberns

Schauen wir uns an, wie die Mischsortierung funktioniert. Angenommen, wir wollen die folgenden Zahlen mit Hilfe des Merge-Sortieralgorithmus ordnen. Der Algorithmus unterteilt die Daten rekursiv in zwei Teile und teilt so lange, bis jede Liste ein Element enthält. Dann kombinieren wir sie, indem wir sie in eine andere Liste sortieren.

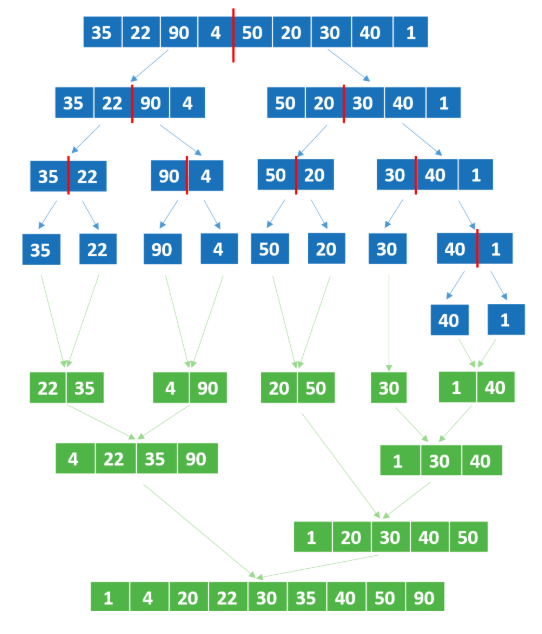
Merge Sort Problem. Quelle: DataCamp

Zeit- und Raumkomplexität von Merge Sort

Es ist unmöglich, im Voraus zu wissen, welcher Sortieralgorithmus für ein bestimmtes Problem am besten geeignet ist. Neben dem Algorithmus müssen mehrere Variablen berücksichtigt werden, darunter die Programmiersprache, in der der Code geschrieben wurde, die Hardware, auf der er ausgeführt wird, und die Besonderheiten der zu sortierenden Daten. 

Auch wenn wir die genaue Laufzeit eines Sortieralgorithmus nicht vorhersagen können, können wir dennoch die Leistung verschiedener Sortieralgorithmen vergleichen, indem wir die Zeit- und Raumkomplexität analysieren.

Zeitliche Komplexität der Mischsortierung

Wie wir in einem separaten Leitfaden zur Big O Notation und Zeitkomplexität erklärt haben, besteht das Ziel der Zeitkomplexitätsanalyse nicht darin, die exakte Laufzeit eines Algorithmus vorherzusagen, sondern vielmehr zu bewerten, wie effizient ein Algorithmus ist, indem wir analysieren, wie sich seine Laufzeit mit zunehmender Menge an Eingabedaten verändert.

Die Analyse der Zeitkomplexität wird in der Big O-Notation geschrieben, einer mathematischen Notation, die die Geschwindigkeit beschreibt, mit der eine Funktion wächst oder abnimmt. Die Merge-Sortierung hat eine logarithmische oder linearithmische Zeitkomplexität, die mit O(N log(N)) angegeben wird, wobei N die Anzahl der Elemente in der Liste ist. Der Buchstabe "O" steht für die "Ordnung" des Wachstums. 

Bei der Analyse der Zeitkomplexität verhält sich die linearithmische Komplexität in etwa so wie die lineare Komplexität, d.h. ihre Ausführung ist direkt proportional zur Datenmenge. Wenn sich also die Datenmenge verdoppelt, sollte sich auch die Zeit verdoppeln, die der Algorithmus braucht, um die Daten zu verarbeiten, d.h. die Anzahl der Teilungen und Zusammenführungen wird sich verdoppeln.

Da sich die Zeitkomplexität von Merge Sort linear verhält, bleibt die Komplexität für den besten, den durchschnittlichen und den schlechtesten Fall gleich. Das bedeutet, dass der Algorithmus unabhängig von der Eingabereihenfolge immer die gleiche Anzahl von Schritten benötigt, um ihn abzuschließen.

Raumkomplexität der Mischsortierung

Ein weiterer wichtiger Aspekt bei der Analyse der Komplexität von Algorithmen ist neben der Zeit, die für die Lösung der Aufgabe benötigt wird, die Abschätzung, wie viel Speicherplatz der Algorithmus benötigt, wenn das Problem größer wird. 

Dies wird durch die Konzepte der Raumkomplexität und des Hilfsraums abgedeckt. Letzteres bezieht sich auf den zusätzlichen oder temporären Speicherplatz, der von einem Algorithmus verwendet wird, während Ersteres sich auf den gesamten Speicherplatz bezieht, den der Algorithmus in Bezug auf die Eingabegröße benötigt. Mit anderen Worten: Die Raumkomplexität umfasst sowohl den Hilfsraum als auch den von der Eingabe verwendeten Raum.

Merge Sort hat eine Raumkomplexität von O(N). Das liegt daran, dass ein Hilfsarray der Größe N verwendet wird, um die sortierten Hälften des Eingangsarrays zusammenzuführen. Das Hilfsarray wird verwendet, um das zusammengeführte Ergebnis zu speichern, und das Eingabearray wird mit dem sortierten Ergebnis überschrieben.

Merge Sort Implementation in Python

Lass uns den Merge-Sortieralgorithmus in Python implementieren. Es gibt mehrere Möglichkeiten, den Algorithmus zu kodieren; wir werden uns jedoch an die auf Rekursion basierende Variante halten, die wohl am einfachsten zu verstehen ist und weniger Codezeilen erfordert als andere Alternativen, die auf Iteration basieren.

Die Rekursion in der Mischsortierung verstehen

Falls du dich mit dem Thema nicht auskennst: In der Programmierung passiert eine Rekursion, wenn eine Funktion sich selbst aufruft. In unserem Tutorial Rekursive Funktionen in Python verstehen kannst du alles über diese mächtigen Funktionen erfahren.

Um Merge Sort zu implementieren, definieren wir zunächst den Basisfall: Wenn die Liste nur ein Element hat, ist sie bereits sortiert, also kehren wir sofort zurück. Andernfalls teilen wir die Liste in zwei Hälften, left_half und right_half, und rufen merge_sort() rekursiv auf jeder dieser Hälften auf. Dieser Prozess wird fortgesetzt, bis alle Unterlisten ein einziges Element enthalten.

Sobald wir diese sortierten Teillisten haben, beginnen wir mit dem Zusammenführungsprozess. Dazu initialisieren wir drei Indexvariablen: i für die Verfolgung der Position in left_half, j für right_half und k für die endgültige zusammengeführte Liste. Dann vergleichen wir die Elemente aus beiden Hälften. Wenn das aktuelle Element in left_half kleiner ist, platzieren wir es in my_list[k] und verschieben i nach vorne. Andernfalls nehmen wir das Element von right_half, legen es in my_list[k] ab und erhöhen j. Nach jedem Vergleich rücken wir k an die nächste Position in der endgültigen Liste vor.

Dieser Prozess wird fortgesetzt, bis wir alle Elemente in einer der Hälften verglichen haben. Wenn Elemente in left_half oder right_half übrig bleiben, werden sie direkt an die endgültige Liste angehängt, um sicherzustellen, dass keine Daten zurückbleiben. Da Merge Sort rekursiv arbeitet, wird dieser Zusammenführungsprozess auf jeder Ebene der Rekursion ausgeführt, bis die gesamte Liste sortiert ist.

Python-Implementierung

Unten findest du den Code, der die unsortierte Liste aus dem vorherigen Diagramm als Beispiel verwendet:

def merge_sort(my_list):
    if len(my_list) > 1: 
        mid = len(my_list)//2
        left_half = my_list[:mid]
        right_half = my_list[mid:]
       
        merge_sort(left_half)
        merge_sort(right_half)

        i = j = k = 0
 
        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                my_list[k] = left_half[i]                
                i += 1
            else:
                my_list[k] = right_half[j]
                j += 1
            k += 1
     
        while i < len(left_half):
            my_list[k] = left_half[i]
            i += 1
            k += 1
 
        while j < len(right_half):
            my_list[k] = right_half[j]
            j += 1
            k += 1

my_list = [35,22,90,4,50,20,30,40,1]
merge_sort(my_list)
print(my_list)
>>> [1, 4, 20, 22, 30, 35, 40, 50, 90]

Merge Sort im Vergleich zu anderen Sortieralgorithmen

Merge Sort ist ein ziemlich schneller Sortieralgorithmus, der sich besonders gut für große Datenbanken eignet und oft als Benchmark für andere Algorithmen verwendet wird. Bei kürzeren Listen ist seine Leistung jedoch tendenziell geringer als bei anderen Sortieralgorithmen.

In der folgenden Tabelle findest du einen Vergleich von Merge Sort mit anderen gängigen Sortieralgorithmen.

Praktische Anwendungen von Merge Sort

Merge Sort hat eine hohe Leistung beim Sortieren von großen Listen, aber seine Effizienz nimmt ab, wenn du mit kleineren Listen arbeitest. Außerdem ist sie in Szenarien, in denen die Eingabelisten bereits einen gewissen Grad an Ordnung aufweisen, weniger effizient, da die Merge-Sortierung unabhängig von der Reihenfolge der Liste dieselben Schritte durchführt.

Ein großartiger Anwendungsfall, bei dem die Mischsortierung besonders nützlich ist, sind verknüpfte Listen. Eine verkettete Liste ist eine Datenstruktur, die aus einer Verbindung von linear miteinander verknüpften Knoten besteht. Jeder Knoten enthält die Daten und den Link, der ihn mit dem nächsten Knoten verbindet.

Die Merge-Sortierung wird für verknüpfte Listen bevorzugt, weil sie nur einen sequentiellen Zugriff auf die Daten erfordert, was der Natur von verknüpften Listen entspricht. Außerdem ist Merge-Sort ein stabiler Sortieralgorithmus (d.h. er behält die relative Reihenfolge gleicher Elemente in der sortierten Ausgabe bei), was für die Beibehaltung der Reihenfolge von verknüpften Listen sehr wichtig ist.

Häufige Fehler und Fehlersuche

Der Merge-Sortieralgorithmus ist ziemlich einfach, und der Spielraum für Verbesserungen im Code ist begrenzt. Du kannst die Komplexität deiner Sortierstrategie jedoch erhöhen, indem du die Größe der Eingabedaten berücksichtigst. 

Wir haben bereits festgestellt, dass die Mischsortierung bei größeren Datensätzen besser funktioniert. Für kleinere Datenmengen sind andere Sortieralgorithmen mit einer Zeitkomplexität von O(N^2), wie z.B. Insertion Sort, besser geeignet. In diesem Fall müsstest du nur eine Größenschwelle festlegen, unterhalb derer du den Algorithmus der Einfügesortierung anstelle der Zusammenführung und Sortierung anwendest.

Ansonsten wäre eine gute Idee, die Parallelisierung zu untersuchen. Die Schritte der Mischsortierung können mit der richtigen Rechenleistung leicht parallelisiert werden, wodurch sich die Zeit bis zur Fertigstellung verkürzt. Lies unseren Leitfaden CPU vs. GPU, um mehr über paralleles Rechnen zu erfahren. 

Fazit

Merge Sort ist einer der effektivsten und beliebtesten Sortieralgorithmen, aber es gibt noch viel mehr zu lernen im wunderbaren und sich ständig erweiternden Universum der Algorithmen. Wenn du dich für die technischen Details von Algorithmen, ihre Funktionsweise und die damit verbundene Komplexität sowie ihre Vor- und Nachteile interessierst, können dir diese DataCamp-Ressourcen helfen, dich weiterzubilden:

• Kurs Einführung in Datenstrukturen und Algorithmen 
• Lernpfad zur Python-Programmierung
• Python Data Fundamentals Lernpfad
• Python-Kurs für Fortgeschrittene
• Lernpfad Datenanalyst in Python 
• Big O Notation und Zeitkomplexität