Qu'est-ce que l'erreur type ? La clé de la précision et de la fiabilité statistiques

Lorsqu'un chercheur médical affirme qu'un nouveau médicament réduit la pression artérielle de 15 points en moyenne, dans quelle mesure pouvons-nous nous fier à cette affirmation ? La réponse réside souvent dans la compréhension de l'erreur type, qui est une mesure statistique indiquant le degré de précision réel de nos estimations d'échantillon.

William Sealy Gosset, écrivant sous le pseudonyme « Student » alors qu'il travaillait à la brasserie Guinness, a développé la théorie des petits échantillons à partir de défis réels rencontrés dans le domaine du brassage. Ses travaux nous ont fourni les fondements mathématiques permettant de faire des déductions fiables lorsque nous ne connaissons pas les paramètres réels de la population.

Ce guide présente les concepts clés, les formules mathématiques et les applications pratiques de l'erreur type dans différents contextes statistiques. Notre échantillonnage dans R couvre plus en détail les principes qui sous-tendent ces calculs et explique comment l'erreur type est liée à l'écart type de l'échantillon vous donne une base solide pour l'inférence statistique.

Qu'est-ce que l'erreur type ?

L'erreur type fournit une mesure de l'incertitude entourant les statistiques d'échantillon, ce qui nous aide à comprendre dans quelle mesure nos estimations pourraient varier si nous répétions la même étude plusieurs fois. Nous examinons le concept fondamental et explorons les différentes formes que prend l'erreur type dans diverses analyses statistiques.

Concept fondamental et intuition

L'erreur type mesure la variabilité d'une statistique d'échantillon parmi des échantillons répétés provenant de la même population. Considérez cela comme une réponse à la question suivante : « Si je recueillais 100 échantillons différents de même taille, dans quelle mesure les moyennes de mes échantillons varieraient-elles ? »

Ce concept découle directement de la théorie de la distribution d'échantillonnage. Lorsque nous calculons une moyenne d'échantillon, cette valeur ne représente qu'un résultat possible parmi de nombreux échantillons potentiels. L'erreur type quantifie la distance typique entre toute statistique d'échantillon individuelle et le paramètre de population réel que nous essayons d'estimer.

L'erreur type mesure la qualité avec laquelle une statistique d'échantillon estime un paramètre de population. Une erreur type plus faible signifie que des échantillons répétés produiraient des estimations similaires, ce qui suggère que notre échantillon actuel fournit une approximation fiable. Une erreur type plus importante suggère une variabilité substantielle entre les échantillons potentiels, ce qui indique une confiance moindre dans notre estimation.

Plusieurs types d'erreurs types

Il n'existe pas une seule erreur standard. Différentes statistiques nécessitent des formules spécialisées en fonction de ce que nous mesurons. Les types les plus courants comprennent :

• Erreur type de la moyenne: Utilisé pour estimer les moyennes de population
• Erreur type d'une proportion: Appliqué aux estimations de pourcentage ou de taux
• Erreur type de la différence entre les moyennes: Utilisé pour comparer deux groupes
• Erreur type des coefficients de régression: Appliqué aux estimations de pente dans les modèles linéaires

Chaque type répond à des objectifs analytiques spécifiques et traite différentes sources de variabilité. Par exemple, l'erreur type d'une proportion tient compte de la nature binomiale des réponses oui/non, tandis que l'erreur type d'une pente de régression prend en considération à la fois la variation résiduelle et la dispersion des valeurs prédictives.

Il est important de choisir le bon type. L'utilisation d'une formule inappropriée peut conduire à des conclusions trop optimistes ou à la négligence d'effets importants.

Fondements conceptuels de l'erreur type

Cette section examine comment l'erreur type s'appuie sur la théorie de l'échantillonnage et le raisonnement statistique, fournissant ainsi les fondements théoriques qui rendent les calculs de l'erreur type à la fois significatifs et fiables.

Théorie de la distribution d'échantillonnage

Le concept de distribution d'échantillonnage fournit la base théorique de l'erreur type. Si nous pouvions collecter tous les échantillons possibles de taille n à partir d'une population et calculer la statistique d'intérêt pour chaque échantillon, nous créerions une distribution d'échantillonnage. L'erreur type est égale à l'écart type de cette distribution théorique d'échantillonnage, ce qui explique pourquoi elle quantifie la variation des statistiques individuelles de l'échantillon par rapport au paramètre réel de la population.

La taille de l'échantillon est inversement proportionnelle à l'erreur type. À mesure que la taille de l'échantillon augmente, l'erreur type diminue proportionnellement à la racine carrée de n. Le théorème de la limite centrale ajoute que les distributions d'échantillonnage tendent vers la normalité à mesure que la taille de l'échantillon augmente, quelle que soit la distribution de la population sous-jacente. Cette hypothèse de normalité nous permet de construire des intervalles de confiance et des tests d'hypothèse à l'aide de l'erreur type, même avec des données non normales, à condition que la taille de l'échantillon soit suffisamment grande.

Facteurs influençant l'ampleur

Trois facteurs déterminent l'ampleur de l'erreur type : la taille de l'échantillon, la variabilité de la population et le plan d'échantillonnage. La variabilité de la population influe directement sur l'erreur type. Des populations plus variables produisent des erreurs types plus importantes pour une taille d'échantillon donnée. Une enquête sur les revenus des ménages dans les zones urbaines présentant des disparités de richesse extrêmes produira des erreurs types plus importantes que dans les communautés rurales où les revenus sont homogènes, même avec des échantillons de taille identique.

La taille de l'échantillon offre l'influence la plus contrôlable grâce à la relation inverse de la racine carrée. Pour réduire l'erreur type de moitié, il est nécessaire de quadrupler la taille de l'échantillon. La conception de l'échantillonnage est également importante : l'échantillonnage en grappes augmente généralement l'erreur type, car les observations au sein des grappes ont tendance à être similaires, tandis que l'échantillonnage stratifié peut réduire l'erreur type en garantissant la représentativité des sous-groupes

Erreur type, taille de l'échantillon et loi des grands nombres

La loi des grands nombres explique pourquoi l'erreur type diminue lorsque les échantillons sont plus grands. Les statistiques d'échantillon convergent vers les paramètres de population à mesure que la taille de l'échantillon augmente. L'erreur type est proportionnelle à 1/√n. C'est pourquoi des échantillons de grande taille sont nécessaires pour obtenir des améliorations significatives en termes de précision. Quadrupler la taille de l'échantillon ne réduit que de moitié l'erreur type.

Cependant, il existe un inconvénient : si des échantillons plus importants réduisent l'erreur type et augmentent la précision, des échantillons extrêmement importants peuvent produire des résultats statistiquement significatifs pour des différences insignifiantes qui n'ont aucune importance pratique. Une étude portant sur 100 000 personnes pourrait détecter une différence de 0,1 point dans la pression artérielle, statistiquement significative mais cliniquement non pertinente. Les petits échantillons peuvent omettre des effets importants en raison d'erreurs types importantes. Il est nécessaire de trouver un équilibre entre la signification statistique et la signification pratique.

Formulation mathématique et calcul

En passant de la compréhension conceptuelle aux procédures de calcul, les formules mathématiques et les calculs étape par étape rendent l'erreur type pratique pour l'analyse des données.

Équations fondamentales pour différents scénarios

La formule de base pour l'erreur type de la moyenne dépend de la connaissance ou non de l'écart type de la population. Lorsque nous disposons de cette information, nous utilisons directement le paramètre de population :

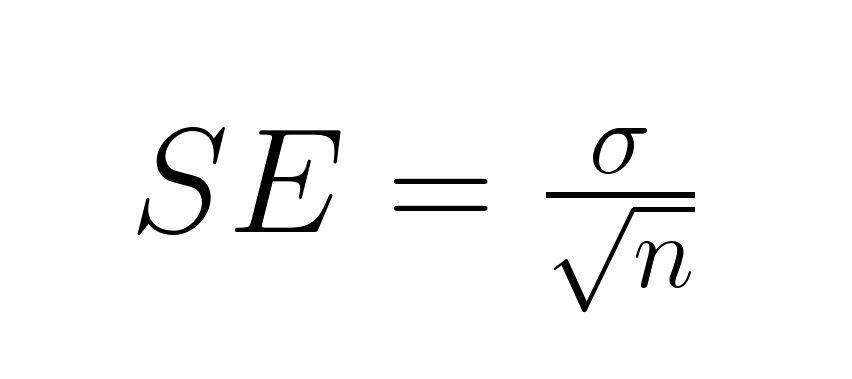
Où :

• σ = écart type de la population
• n = taille de l'échantillon

Plus généralement, l'écart type de la population est inconnu, nous le remplaçons donc par l'écart type de l'échantillon, ce qui introduit une incertitude supplémentaire qui nécessite de se référer à la distribution t :

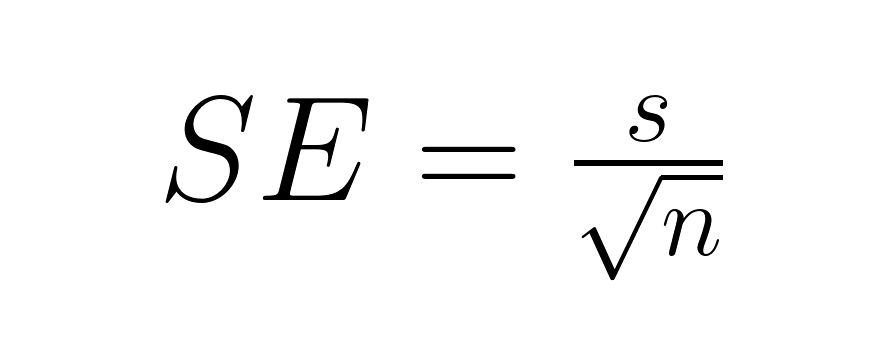
Où :

• s = écart type de l'échantillon
• n = taille de l'échantillon

L'erreur type d'une proportion traite les résultats binaires à l'aide de la formule de distribution binomiale :

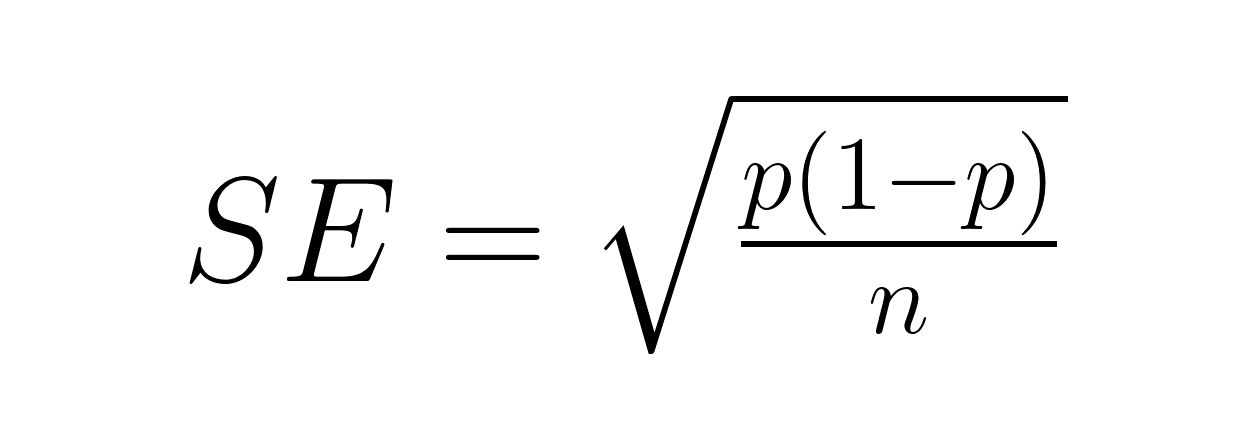
Où :

• p = proportion de l'échantillon
• n = taille de l'échantillon

L'erreur type d'une pente de régression implique à la fois la variation résiduelle et la dispersion des variables prédictives :

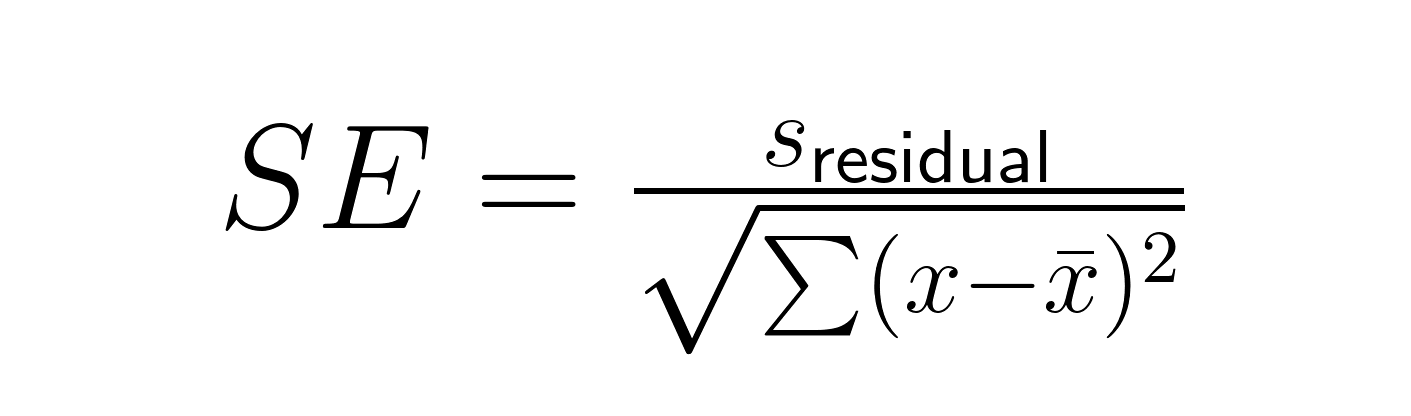
Où :

• srésiduel = erreur type résiduelle de la régression
• x = valeurs prédictives individuelles
• x̄ = moyenne des valeurs prédictives

L'erreur type de la différence entre les moyennes varie selon que les groupes sont indépendants ou appariés. Pour les groupes indépendants :

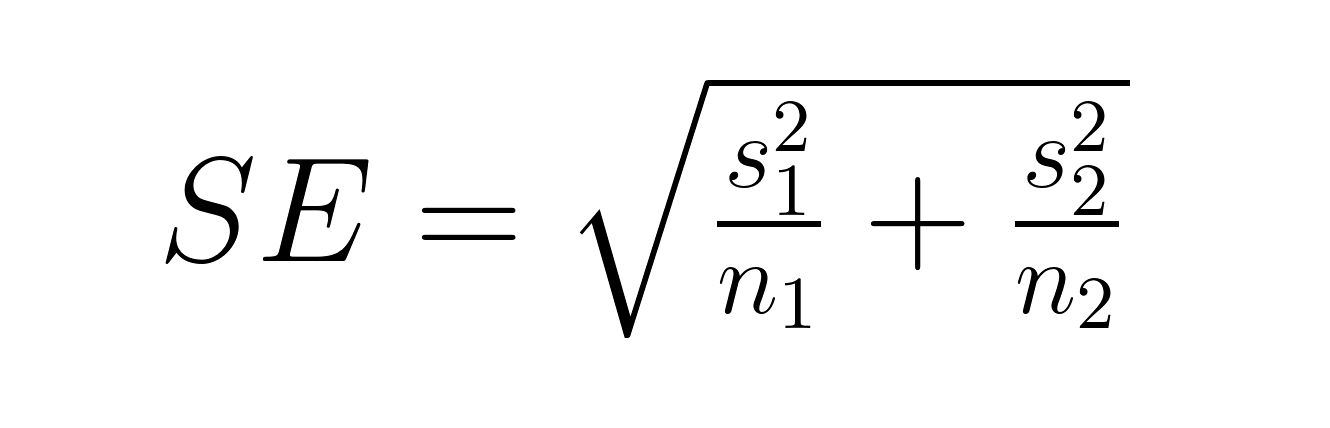
Où :

• s₁, s₂ = écarts types des groupes 1 et 2
• n₁, n₂ = tailles des échantillons des groupes 1 et 2

Pour les comparaisons par paires, la formule se simplifie considérablement :

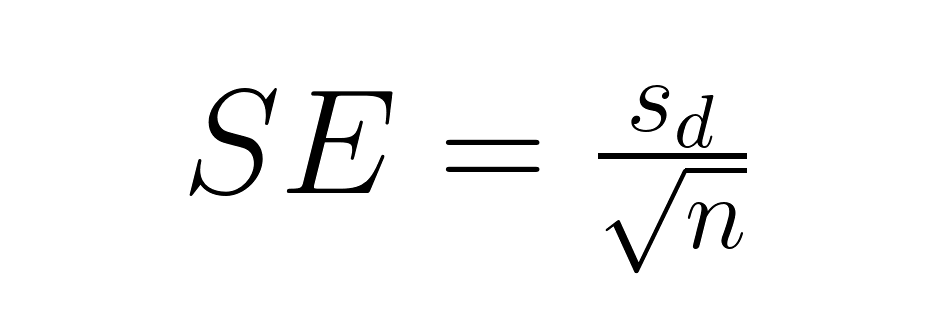
Où :

• sd = écart type des différences appariées
• n = nombre de paires

Procédures de calcul et scénarios

Les paramètres de population connus représentent le scénario idéal permettant d'utiliser la distribution normale pour l'inférence. Paramètres inconnus reflètent des situations de recherche typiques dans lesquelles nous effectuons des estimations à partir d'échantillons de données en utilisant un processus en trois étapes :

Étape 1 : Veuillez calculer la moyenne de l'échantillon. 

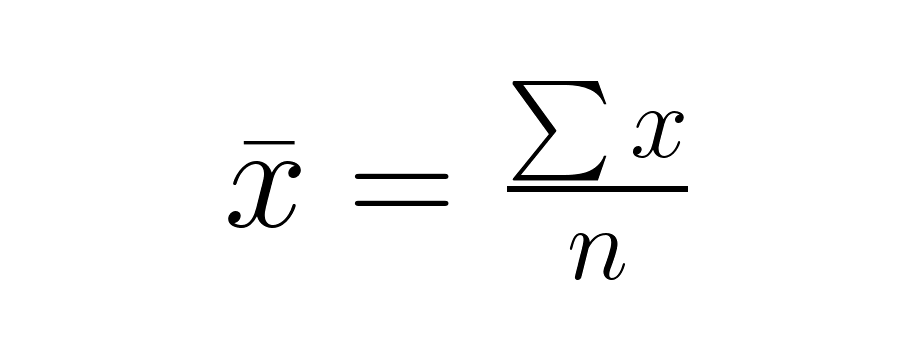
Étape 2 : Veuillez calculer l'écart type de l'échantillon. 

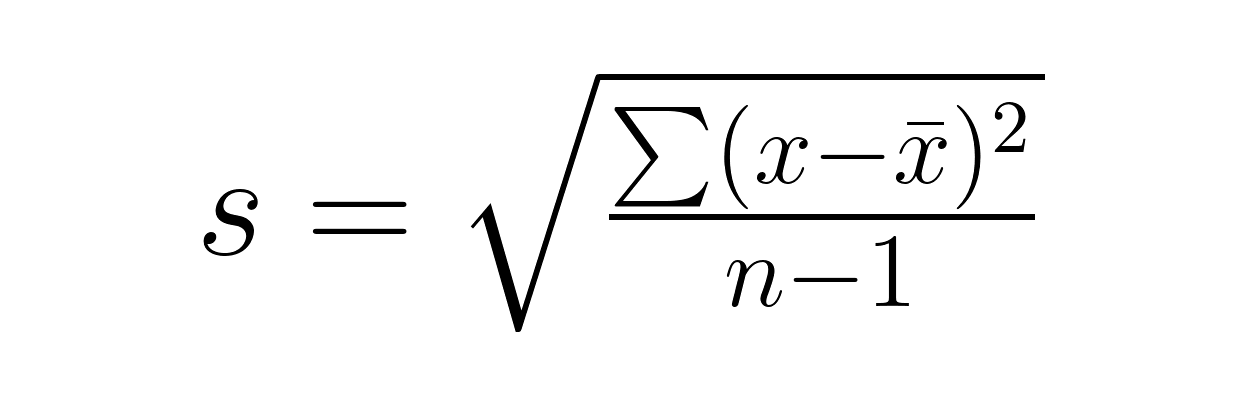
Étape 3 : Appliquez la formule appropriée de l'erreur type en utilisant l'écart type de l'échantillon.

Interprétation: Des erreurs types plus faibles indiquent des estimations plus précises. Une erreur type de 2,5 pour une moyenne d'échantillon de 50 suggère que la moyenne réelle de la population se situe probablement entre 45 et 55 environ, tandis qu'une erreur type de 10 indique une incertitude beaucoup plus grande. Dans des conditions de normalité approximative, environ 68 % se situent à moins d'une écart-type et environ 95 % à moins de 1,96 écart-type de la moyenne réelle. Pour les petits échantillons utilisant s, veuillez utiliser les valeurs critiques t.

Extensions et corrections

La correction pour population finie (FPC) devient nécessaire lorsque l'échantillonnage dépasse 5 % d'une population finie :

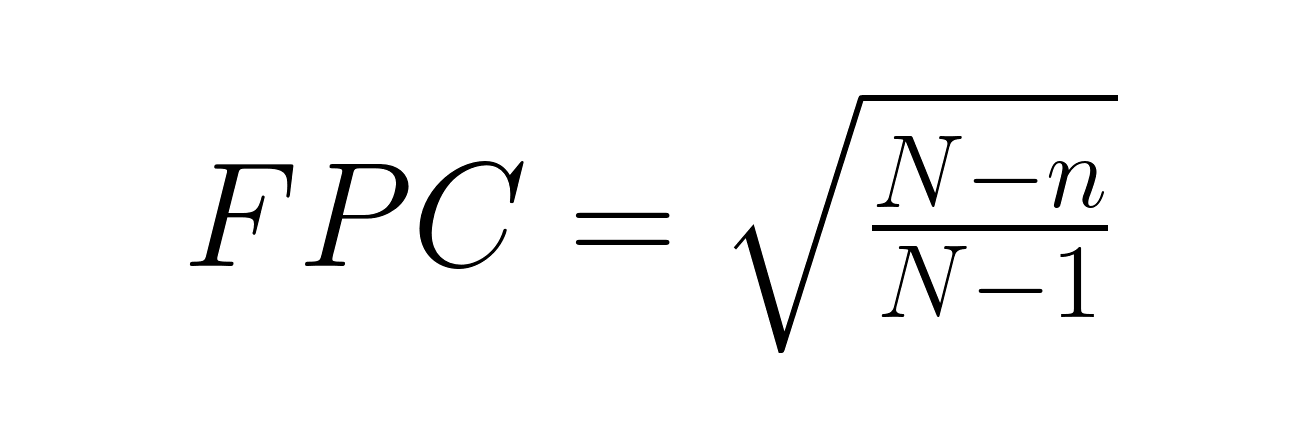
Où :

• N = taille totale de la population
• n = taille de l'échantillon

L'erreur type corrigée devient :

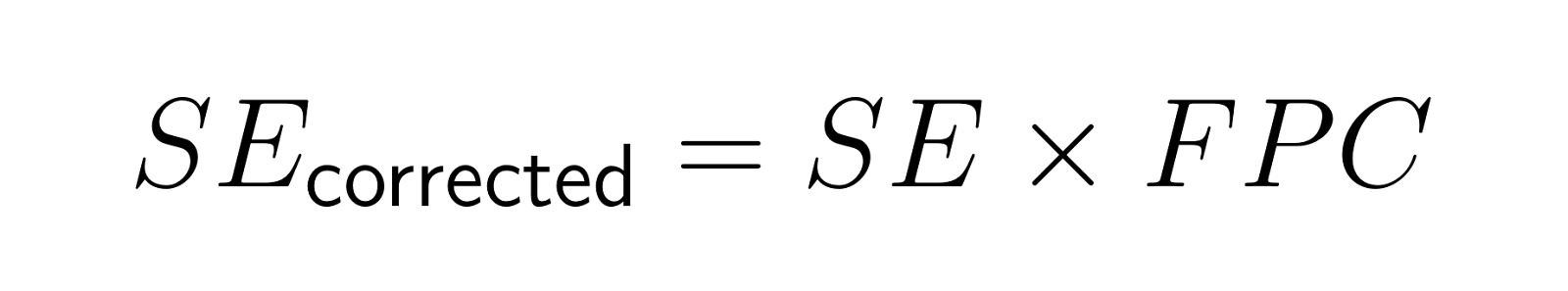
Par exemple, une enquête menée auprès de 200 personnes dans une ville de 2 000 habitants donne un facteur de correction d'environ 0,95, ce qui réduit l'erreur type de 5 %.

Les échantillons groupés nécessitent des ajustements pour réduire la taille effective de l'échantillon à l'aide de l'effet de conception :

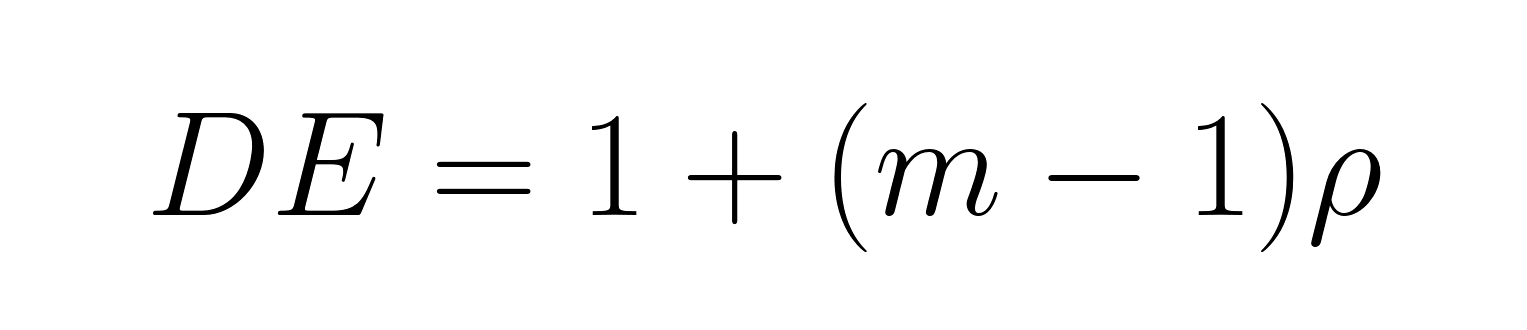
Où :

• m = taille moyenne des grappes
• ρ = coefficient de corrélation intra-cluster (degré de similitude entre les observations au sein des clusters)

L'erreur type ajustée devient :

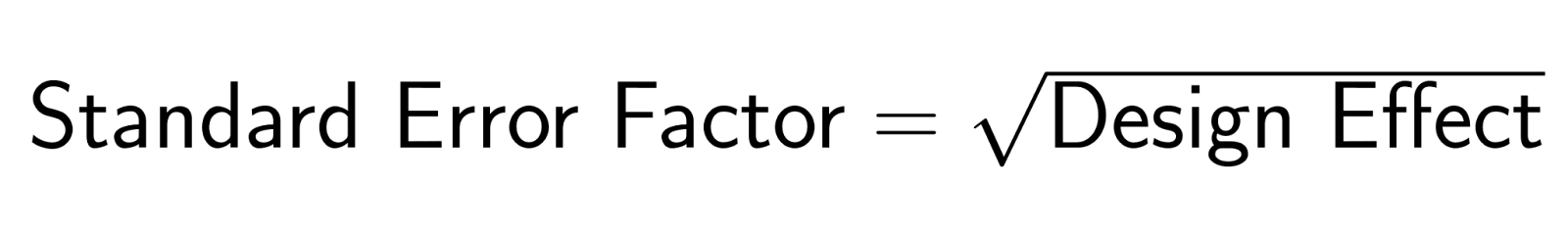
Lorsque les membres d'une famille ont des opinions similaires (ρ = 0,3) et que la taille moyenne du ménage est de 3, l'effet de conception est DE = 1 + (3-1)(0,3) = 1,6. Le facteur d'erreur type est √1,6 = 1,27, ce qui rend les erreurs types 27 % plus importantes que celles obtenues avec un échantillonnage aléatoire simple.

Applications en inférence statistique

L'erreur type est à la base de certaines des techniques les plus importantes en matière d'inférence statistique, des intervalles de confiance aux tests d'hypothèse. Cette section examine comment l'erreur type rend ces procédures fondamentales possibles et fiables.

Construction d'intervalles de confiance

L'erreur type détermine directement l' intervalle de confiance :

Pour les échantillons de grande taille, la valeur critique est d'environ 1,96 pour un niveau de confiance de 95 %. Les échantillons plus petits utilisent des valeurs critiques de distribution t légèrement plus élevées. Cette relation explique pourquoi les chercheurs indiquent souvent les erreurs types en plus des estimations ponctuelles. Ils fournissent un aperçu immédiat de la précision des résultats.

Les intervalles étroits indiquent des estimations précises avec de faibles erreurs types, tandis que les intervalles larges suggèrent une incertitude importante. Le niveau de confiance (95 %, 99 %, etc.) détermine le degré de confiance souhaité, mais la largeur de l'intervalle dépend fortement de l'erreur type.

Cadre de test d'hypothèses

L'erreur type normalise les statistiques de test en convertissant les différences brutes en unités de variabilité d'échantillonnage :

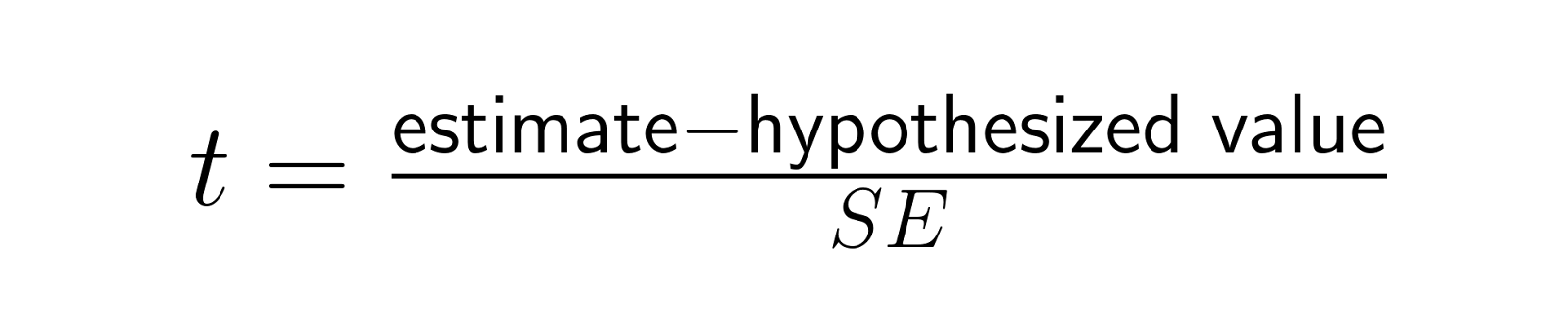
Cette statistique t permet une comparaison pertinente entre différentes études et différentes tailles d'effet en exprimant les différences par rapport à leur variabilité attendue sous l'hypothèse nulle. Une différence de 5 points peut être significative avec SE = 1 (donnant t = 5), mais insignifiante avec SE = 10 (donnant t = 0,5), ce qui illustre comment l'erreur type fournit le contexte nécessaire à l'interprétation de la taille des effets.

Étant donné que les tests statistiques divisent l'effet observé par l'erreur type, des erreurs types plus faibles permettent même à des effets réels modestes d'atteindre une signification statistique, tandis que des erreurs types plus importantes nécessitent des effets plus importants pour atteindre cette signification. Cela explique pourquoi les études à grande échelle peuvent détecter des effets modestes mais réels qui échapperaient à des études de moindre envergure.

Applications méta-analytiques

Dans la méta-analyse, l'erreur type détermine le poids attribué à chaque étude par le biais de la pondération par l'inverse de la variance :

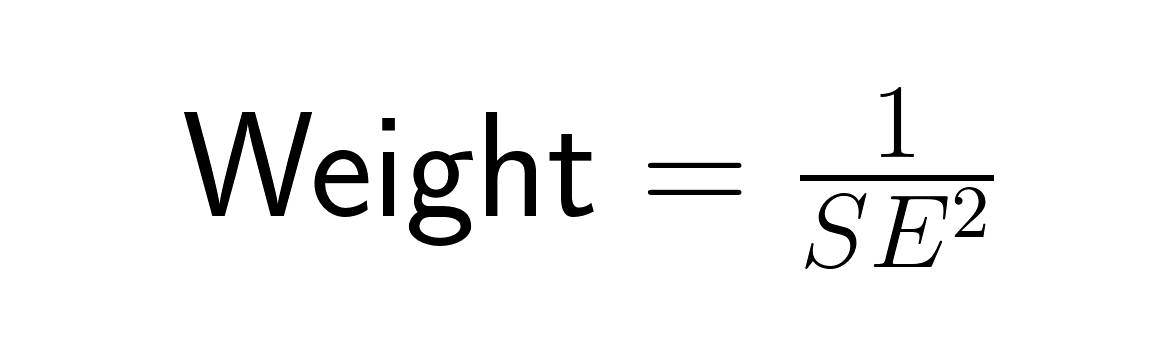
Les études présentant des erreurs types plus faibles (estimations plus précises) ont plus de poids que celles présentant des erreurs types plus importantes, conformément au principe selon lequel les estimations plus précises devraient contribuer davantage à notre compréhension globale. Une étude présentant une erreur type de 0,5 reçoit quatre fois plus de poids qu'une étude présentant une erreur type de 1,0, ce qui permet de combiner de manière optimale les informations issues des différentes études afin de minimiser l'erreur type globale de l'estimation méta-analytique.

Rapport et interprétation de l'erreur type

Une communication claire concernant l'erreur type nécessite une attention particulière tant au format de présentation qu'au contexte d'interprétation. Vous trouverez ci-dessous des conseils pratiques pour présenter les résultats des erreurs types et éviter les erreurs d'interprétation courantes. 

Meilleures pratiques en matière de reporting

Veuillez toujours préciser le type d'erreur standard que vous signalez et utilisez un format cohérent. Veuillez utiliser des formats tels que « Moyenne (SE) » comme « 45,2 (2,8) » dans les tableaux. Pour les graphiques, veuillez utiliser des barres d'erreur s'étendant d'une erreur type au-dessus et en dessous des estimations ponctuelles, mais précisez clairement si les barres d'erreur représentent l'erreur type, l'écart type ou les intervalles de confiance.

Interprétation dans la régression et les modèles

Les résultats de la régression affichent les erreurs types ainsi que les estimations des coefficients. Un coefficient de 0,75 avec SE = 0,25 suggère que l'effet réel se situe probablement entre environ 0,25 et 1,25, tandis que la statistique t de 3,0 indique une forte preuve contre l'hypothèse nulle.

Considérations relatives aux erreurs non liées à l'échantillonnage

L'erreur type ne quantifie que la variabilité de l'échantillonnage. Il ne tient pas compte des erreurs de mesure, des biais de non-réponse ou d'autres sources d'incertitude. Les biais systématiques, tels que le biais de sélection ou les facteurs de confusion, peuvent entraîner des estimations inexactes, quelle que soit la taille de l'erreur type. Il est important de ne pas laisser de petites erreurs types engendrer une confiance excessive dans des résultats qui pourraient encore être systématiquement biaisés.

Interprétations erronées courantes et pièges à éviter

Une interprétation minutieuse de l'erreur type nécessite de prendre conscience des idées fausses courantes qui peuvent conduire à des conclusions erronées. Cette section traite des sources de confusion les plus courantes et fournit des conseils pour éviter les erreurs d'interprétation.

Erreur type et écart type

L'erreur type et l'écart type mesurent différents aspects de la variabilité et ne doivent pas être confondus, bien que cette confusion apparaisse fréquemment dans les rapports de recherche et les médias grand public. L'écart type décrit la dispersion des observations individuelles autour de la moyenne de l'échantillon, en répondant à la question « Dans quelle mesure les points de données individuels s'écartent-ils de la moyenne ? ». L'erreur type décrit la précision de la moyenne de l'échantillon en tant qu'estimation de la moyenne de la population, en répondant à la question « Dans quelle mesure les moyennes de l'échantillon varieraient-elles si nous répétions l'étude ? ».

La relation mathématique permet de clarifier la distinction :

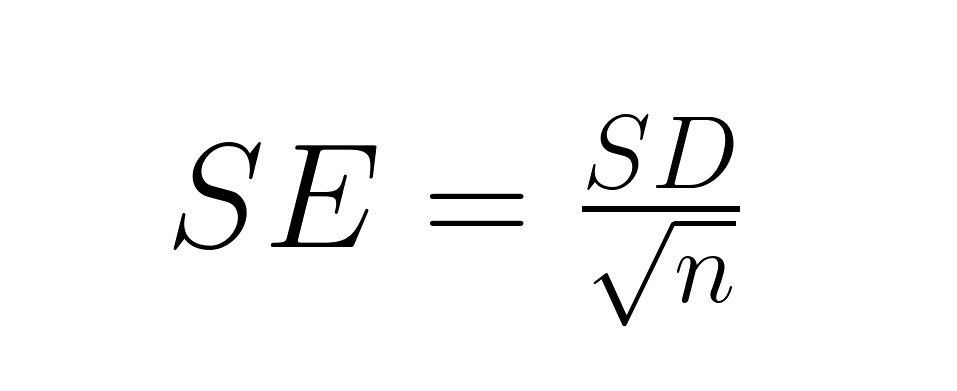
L'erreur type est égale à l'écart type divisé par la racine carrée de la taille de l'échantillon, de sorte que l'erreur type est toujours inférieure à l'écart type (sauf lorsque n = 1). Un ensemble de données sur la taille des adultes peut présenter un écart type de 10 cm (indiquant que la taille varie considérablement d'un individu à l'autre), mais une erreur type de 0,25 cm pour la moyenne de l'échantillon (indiquant une estimation très précise de la taille moyenne). 

Précision et exactitude : idées reçues

L'erreur type mesure la précision, et non l'exactitude. Une petite erreur type indique une grande précision, car des échantillons répétés produiraient des estimations similaires, mais l'exactitude peut être compromise par des biais systématiques.

Prenons l'exemple d'un pèse-personne qui affiche systématiquement 5 livres de trop : se peser 100 fois donnerait des mesures très précises (petite erreur type), mais des résultats systématiquement inexacts. Une faible erreur type ne garantit pas des résultats corrects.

Inconvénients et limites

Les calculs d'erreur type supposent un échantillonnage aléatoire, des observations indépendantes et souvent une distribution normale. L'échantillonnage non aléatoire rend l'erreur type inappropriée, tandis que les observations corrélées (comme les élèves au sein d'une même école) nécessitent des erreurs types plus importantes.

Veuillez ne pas considérer une faible erreur type comme une « preuve » d'un résultat. Un essai contrôlé randomisé avec une petite erreur type fournit des preuves plus solides qu'une étude observationnelle avec une erreur type tout aussi petite, car la conception de l'étude influe sur la validité, indépendamment de la précision statistique. Notre cours sur la conception expérimentale dans R couvre les principes de randomisation, de blocage et de contrôle expérimental appropriés qui garantissent que vos calculs d'erreur type mènent à des conclusions valides.

Extensions méthodologiques avancées

Les pratiques statistiques modernes ont développé des alternatives et des extensions aux approches classiques de l'erreur type, offrant des solutions lorsque les méthodes traditionnelles s'avèrent insuffisantes ou lorsqu'une quantification plus sophistiquée de l'incertitude est nécessaire.

Les techniques de bootstrapping offrent une approche non paramétrique qui ne repose pas sur des hypothèses de distribution. En rééchantillonnant à plusieurs reprises les données originales, les méthodes bootstrap estiment les erreurs types pour les statistiques complexes pour lesquelles il n'existe pas de formules analytiques. Notre échantillonnage en Python couvre les techniques de bootstrap.

Les erreurs types robustes ajustent les violations des hypothèses. Les erreurs types hétéroscédastiques cohérentes restent valables lorsque la variance résiduelle n'est pas constante, tandis que les erreurs types groupées tiennent compte de la corrélation au sein des groupes. Ces méthodes produisent généralement des erreurs types plus importantes, ce qui permet d'obtenir des inférences plus prudentes.

Les approches bayésiennes quantifient l'incertitude à l'aide de distributions a posteriori plutôt que d'erreurs types. Les intervalles de crédibilité bayésiens fournissent des déclarations de probabilité directes : Il existe une probabilité de 95 % que le paramètre se situe entre 2,1 et 4,7. Découvrez notre cours sur la modélisation bayésienne par régression avec rstanarm pour découvrir comment les méthodes bayésiennes traitent différemment l'incertitude.

Conclusion

L'erreur type relie les données échantillonnées et les inférences sur la population, quantifiant la précision de nos estimations et permettant de tirer des conclusions statistiques significatives. Point essentiel : l'erreur type mesure la précision, et non l'exactitude. Cela nous indique dans quelle mesure nos estimations seraient cohérentes d'un échantillon à l'autre, et non si ces estimations sont correctes.

Utilisez l'erreur type de manière appropriée en vérifiant les hypothèses, en choisissant le type correct et en interprétant les résultats dans le contexte plus large de la conception de l'étude. Veuillez toujours indiquer les erreurs types en plus des estimations ponctuelles, préciser le type que vous utilisez et reconnaître les limites. Envisagez d'explorer des méthodes avancées grâce à notre Inférence statistique dans R pour approfondir vos connaissances grâce au cursus

Que vous conceviez des expériences, analysiez des données d'enquête ou interprétiez des résultats de recherche, l'erreur type fournit la base d'une quantification honnête de l'incertitude qui renforce la confiance dans les résultats statistiques.