Was ist ein Standardfehler? Der Schlüssel zu statistischer Genauigkeit und Zuverlässigkeit

Wenn ein Mediziner sagt, dass ein neues Medikament den Blutdruck um durchschnittlich 15 Punkte senkt, wie sehr können wir dieser Aussage vertrauen? Die Antwort liegt oft im Verständnis des Standardfehlers, einem statistischen Maß, das uns sagt, wie genau unsere Stichprobenabschätzungen wirklich sind.

William Sealy Gosset, der während seiner Zeit bei der Guinness-Brauerei unter dem Pseudonym „Student” schrieb, entwickelte die Theorie der kleinen Stichproben aus echten Herausforderungen beim Brauen. Seine Arbeit hat uns die mathematischen Grundlagen gegeben, um fundierte Schlussfolgerungen zu ziehen, wenn wir die wahren Populationsparameter nicht kennen.

Dieser Leitfaden erklärt die wichtigsten Konzepte, mathematischen Formeln und praktischen Anwendungen des Standardfehlers in verschiedenen statistischen Kontexten. Unsere Kurs „Sampling in R” beschäftigt sich genauer mit den Prinzipien hinter diesen Berechnungen und erklärt, wie der Standardfehler mit der Standardabweichung der Stichprobe, bekommst du eine solide Grundlage für statistische Schlussfolgerungen.

Was ist ein Standardfehler?

Der Standardfehler gibt an, wie unsicher die Stichprobenstatistik ist, und hilft uns zu verstehen, wie stark unsere Schätzungen variieren könnten, wenn wir dieselbe Studie mehrmals machen würden. Wir schauen uns das Kernkonzept an und checken die verschiedenen Formen des Standardfehlers in verschiedenen statistischen Analysen.

Kernkonzept und Intuition

Der Standardfehler zeigt, wie sehr sich eine Stichprobenstatistik über wiederholte Stichproben aus derselben Grundgesamtheit ändern kann. Stell dir vor, du würdest antworten: „Wenn ich 100 verschiedene Proben derselben Größe sammeln würde, wie stark würden meine Stichprobenmittelwerte variieren?“

Dieses Konzept kommt direkt aus der Theorie der Stichprobenverteilung. Wenn wir einen Stichprobenmittelwert berechnen, ist dieser Wert nur ein mögliches Ergebnis aus vielen potenziellen Stichproben. Der Standardfehler zeigt, wie weit eine einzelne Stichprobenstatistik normalerweise vom echten Populationsparameter entfernt ist, den wir schätzen wollen.

Der Standardfehler zeigt, wie gut eine Stichprobenstatistik einen Populationsparameter schätzt. Ein kleinerer Standardfehler heißt, dass wiederholte Stichproben ähnliche Schätzungen ergeben würden, was darauf hindeutet, dass unsere aktuelle Stichprobe eine zuverlässige Annäherung liefert. Ein größerer Standardfehler deutet auf erhebliche Schwankungen zwischen den möglichen Stichproben hin, was bedeutet, dass unsere Schätzung weniger zuverlässig ist.

Verschiedene Arten von Standardfehlern

Es gibt nicht nur einen Standardfehler. Verschiedene Statistiken brauchen ihre eigenen speziellen Formeln, je nachdem, was wir messen. Die häufigsten Arten sind:

• Standardfehler des Mittelwerts: Wird benutzt, um Durchschnittswerte für die Bevölkerung zu schätzen.
• Standardfehler eines Anteils: Angewendet auf Prozent- oder Ratenschätzungen
• Standardfehler der Differenz zwischen den Mittelwerten: Wird benutzt, wenn man zwei Gruppen vergleicht.
• Standardfehler der Regressionskoeffizienten: Angewendet auf Steigungsschätzungen in linearen Modellen

Jeder Typ hat bestimmte Analysezwecke und befasst sich mit unterschiedlichen Ursachen für Variabilität. Zum Beispiel berücksichtigt der Standardfehler eines Anteils die binomiale Natur von Ja/Nein-Antworten, während der Standardfehler einer Regressionssteigung sowohl die Restvariation als auch die Streuung der Prädiktorwerte berücksichtigt.

Die Wahl des richtigen Typs ist wichtig. Wenn man die falsche Formel nimmt, kann das zu übertriebenen Schlussfolgerungen oder übersehenen wichtigen Effekten führen.

Konzeptionelle Grundlagen des Standardfehlers

In diesem Abschnitt geht's darum, wie der Standardfehler in der Stichprobentheorie und im statistischen Denken begründet ist. Das liefert die theoretische Grundlage, die die Berechnung des Standardfehlers sowohl aussagekräftig als auch zuverlässig macht.

Theorie der Stichprobenverteilung

Das Konzept der Stichprobenverteilung ist die theoretische Grundlage für den Standardfehler. Wenn wir alle möglichen Stichproben der Größe n aus einer Grundgesamtheit sammeln und die gewünschte Statistik für jede Stichprobe berechnen könnten, würden wir eine Stichprobenverteilung erstellen. Der Standardfehler ist gleich der Standardabweichung dieser theoretischen Stichprobenverteilung, was erklärt, warum er angibt, wie stark einzelne Stichprobenstatistiken um den wahren Populationsparameter herum variieren.

Die Stichprobengröße hängt umgekehrt vom Standardfehler ab. Wenn die Stichprobengröße größer wird, wird der Standardfehler proportional zur Quadratwurzel von n kleiner. Der Zentrale Grenzwertsatz sagt auch, dass sich Stichprobenverteilungen mit zunehmender Stichprobengröße der Normalverteilung annähern, egal wie die Verteilung der Grundgesamtheit aussieht. Mit dieser Annahme der Normalität können wir auch bei nicht normalverteilten Daten Konfidenzintervalle und Hypothesentests mit dem Standardfehler machen, solange die Stichprobe groß genug ist.

Faktoren, die die Größe beeinflussen

Drei Sachen bestimmen, wie groß der Standardfehler ist: die Größe der Stichprobe, wie unterschiedlich die Grundgesamtheit ist und wie die Stichprobe gemacht wurde. Die Variabilität der Population beeinflusst direkt den Standardfehler. Variablere Populationen führen bei einer bestimmten Stichprobengröße zu größeren Standardfehlern. Eine Umfrage zum Haushaltseinkommen in Städten mit extremen Einkommensunterschieden wird größere Standardfehler ergeben als in ländlichen Gemeinden mit ähnlichen Einkommen, selbst wenn die Stichprobengrößen gleich sind.

Die Stichprobengröße hat den größten Einfluss, weil sie mit der inversen Quadratwurzel zusammenhängt. Um den Standardfehler um die Hälfte zu reduzieren, muss man die Stichprobengröße vervierfachen. Auch das Stichprobenverfahren ist wichtig: Bei Cluster-Stichproben wird der Standardfehler normalerweise größer, weil die Beobachtungen innerhalb der Cluster oft ähnlich sind, während geschichtete Stichproben den Standardfehler verringern können, weil sie sicherstellen, dass alle wichtigen Untergruppen vertreten sind.

Standardfehler, Stichprobengröße und das Gesetz der großen Zahlen

Das Gesetz der großen Zahlen erklärt, warum der Standardfehler bei größeren Stichproben kleiner wird. Die Stichprobenstatistik passt sich den Populationsparametern an, wenn die Stichprobengröße größer wird. Der Standardfehler ist proportional zu 1/√n. Deshalb braucht man riesige Stichproben, um die Genauigkeit richtig zu verbessern. Wenn man die Stichprobengröße vervierfacht, wird der Standardfehler nur halbiert.

Aber es gibt einen Haken: Während größere Stichproben den Standardfehler verringern und die Genauigkeit erhöhen, können extrem große Stichproben statistisch signifikante Ergebnisse für unwesentliche Unterschiede liefern, die keine praktische Bedeutung haben. Eine Studie mit 100.000 Leuten könnte einen statistisch bedeutenden, aber klinisch nicht relevanten Unterschied von 0,1 Punkten beim Blutdruck zeigen. Bei kleinen Stichproben können wichtige Effekte wegen großer Standardfehler übersehen werden. Du musst die statistische Bedeutung mit der praktischen Bedeutung abwägen.

Mathematische Formulierung und Berechnung

Wenn man vom konzeptionellen Verständnis zu den Berechnungsverfahren übergeht, machen die mathematischen Formeln und Schritt-für-Schritt-Berechnungen den Standardfehler für die Datenanalyse praktisch anwendbar.

Grundlegende Gleichungen für verschiedene Szenarien

Die Grundformel für den Standardfehler des Mittelwerts hängt davon ab, ob die Standardabweichung der Grundgesamtheit bekannt ist. Wenn wir den Populationsparameter kennen, nehmen wir ihn direkt:

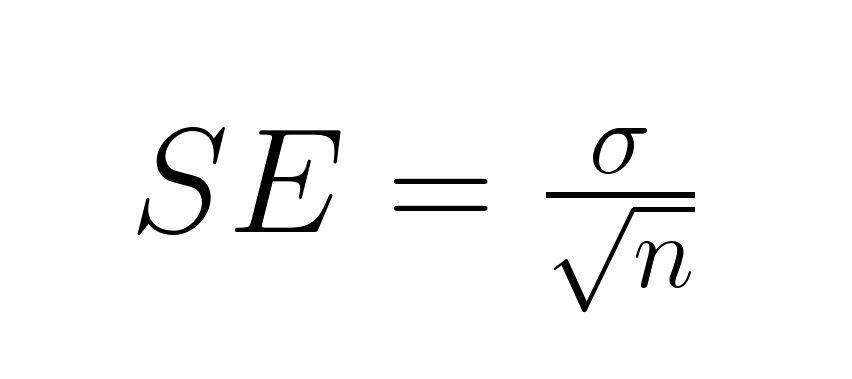
Wo:

• σ = Standardabweichung der Grundgesamtheit
• n = Stichprobengröße

Meistens ist die Standardabweichung der Grundgesamtheit nicht bekannt, also nehmen wir die Stichprobenstandardabweichung und fügen damit eine zusätzliche Unsicherheit hinzu, die uns dazu zwingt, die t-Verteilung zu nutzen:

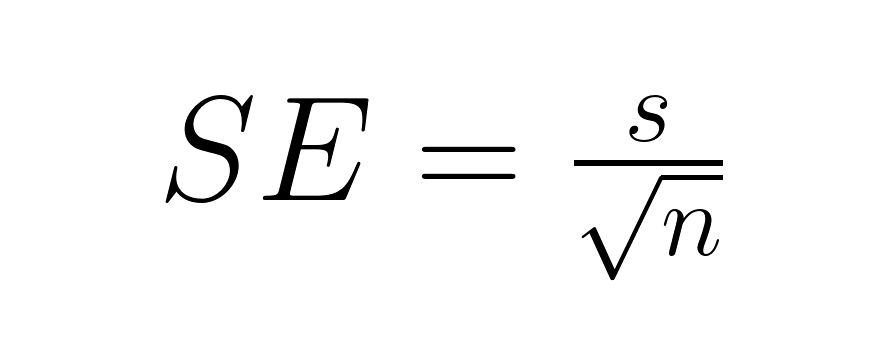
Wo:

• s = Standardabweichung der Stichprobe
• n = Stichprobengröße

Standardfehler eines Anteils befasst sich mit binären Ergebnissen unter Verwendung der Binomialverteilungsformel:

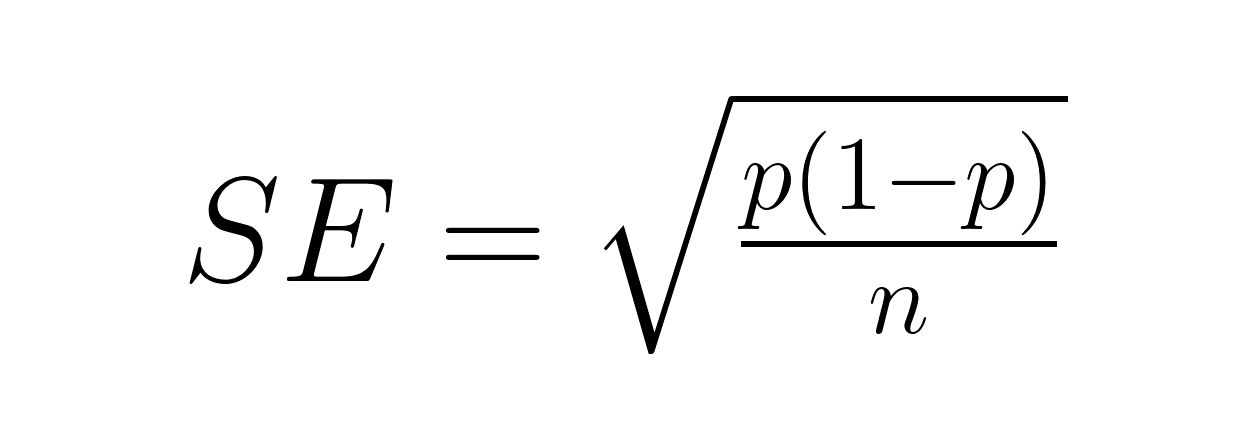
Wo:

• p = Stichprobenanteil
• n = Stichprobengröße

Der Standardfehler einer Regressionssteigung beinhaltet sowohl die Restabweichung als auch die Streuung der Prädiktorvariablen:

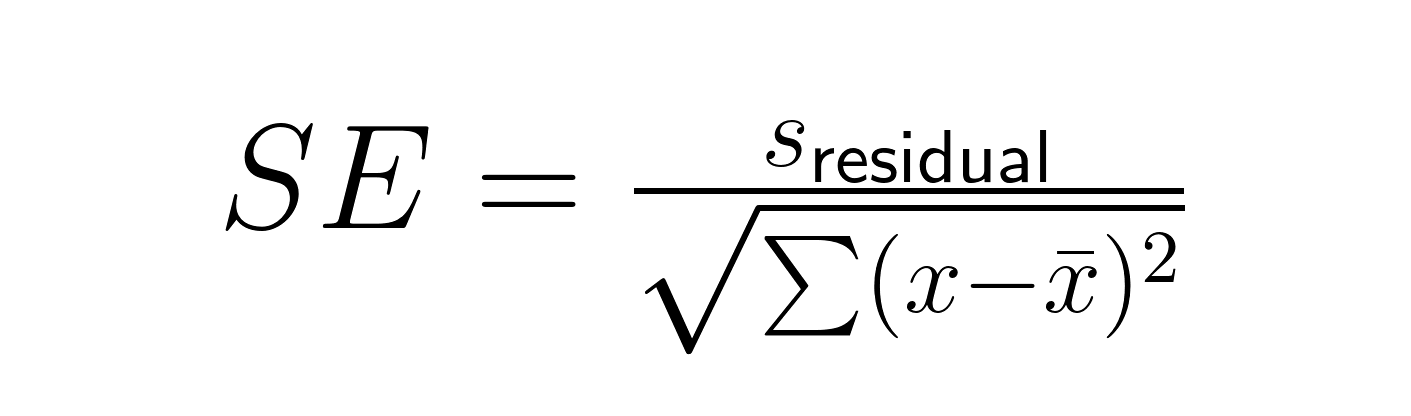
Wo:

• sRestwert = Standardfehler der Regression
• x = einzelne Prädiktorwerte
• x̄ = Mittelwert der Prädiktorwerte

Der Standardfehler der Differenz zwischen den Mittelwerten hängt davon ab, ob die Gruppen unabhängig oder gepaart sind. Für unabhängige Gruppen:

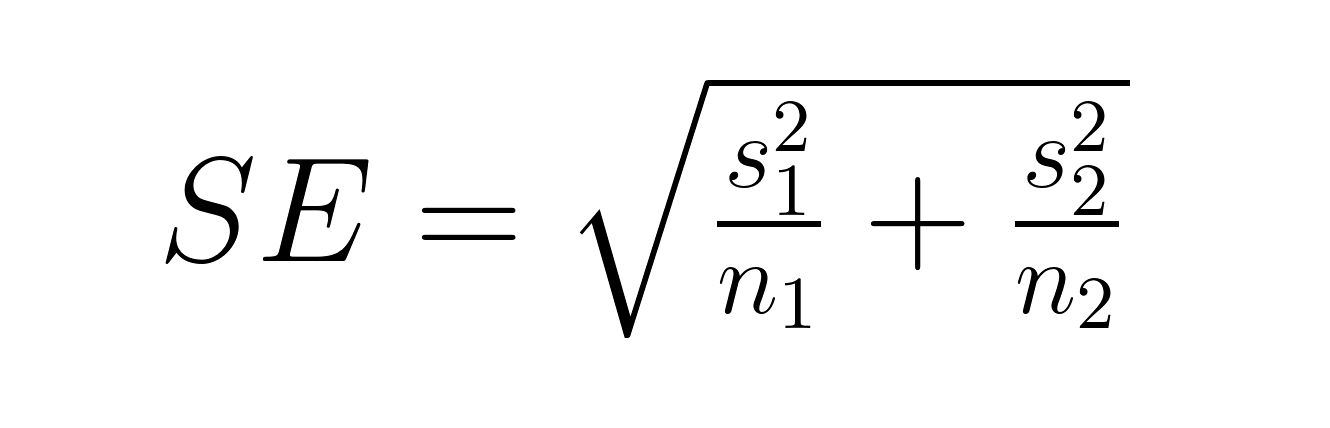
Wo:

• s₁, s₂ = Standardabweichungen der Gruppen 1 und 2
• n₁, n₂ = Stichprobengrößen der Gruppen 1 und 2

Für paarweise Vergleiche wird die Formel echt einfach:

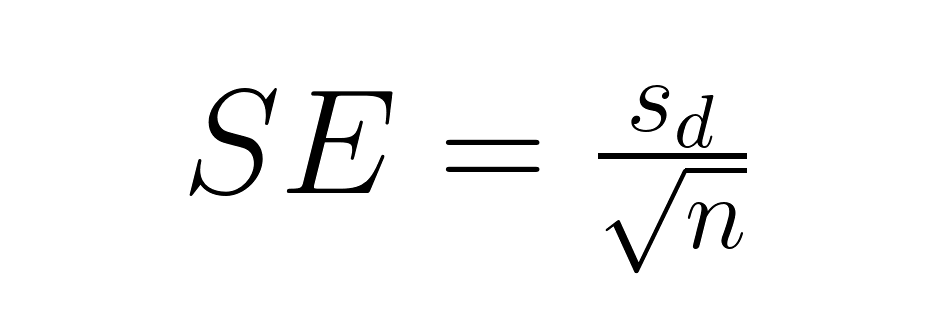
Wo:

• sd = Standardabweichung der gepaarten Differenzen
• n = Anzahl der Paare

Berechnungsverfahren und Szenarien

Die bekannten Populationsparameter zeigen das ideale Szenario, wo man die Normalverteilung für die Schlussfolgerung nutzen kann. Unbekannte Parameter spiegeln typische Forschungssituationen wider, in denen wir anhand von Stichprobendaten in einem dreistufigen Prozess Schätzungen vornehmen:

Schritt 1: Berechne den Stichprobenmittelwert. 

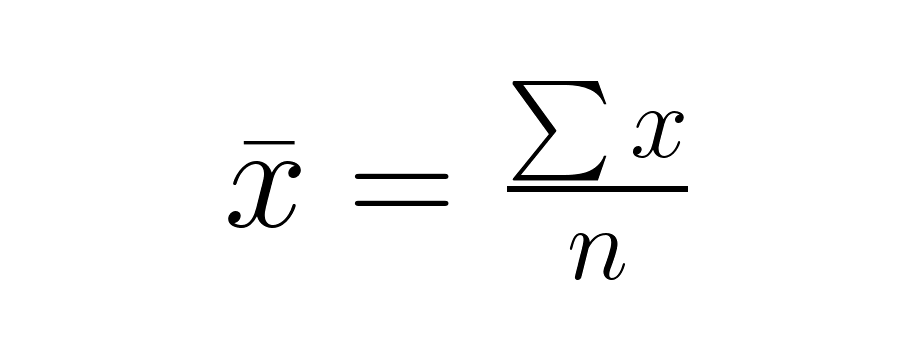
Schritt 2: Berechne die Standardabweichung der Stichprobe. 

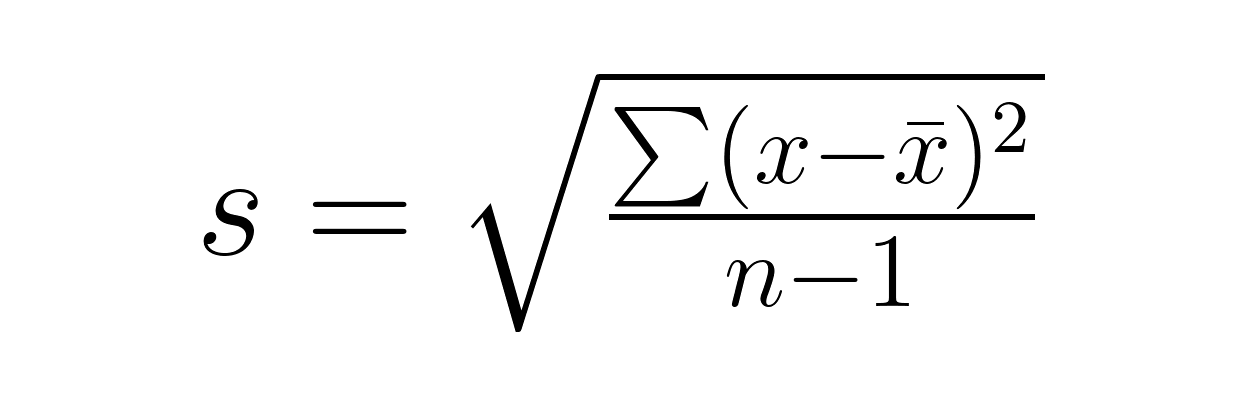
Schritt 3: Wende die passende Standardfehlerformel mit der Stichprobenstandardabweichung an.

Übersetzung: Kleinere Standardfehler bedeuten genauere Schätzungen. Ein Standardfehler von 2,5 für einen Stichprobenmittelwert von 50 deutet darauf hin, dass der wahre Populationsmittelwert wahrscheinlich zwischen 45 und 55 liegt, während ein Standardfehler von 10 eine viel größere Unsicherheit anzeigt. Unter annähernder Normalität liegen etwa 68 % innerhalb von 1 SE und etwa 95 % innerhalb von 1,96 SE vom wahren Mittelwert. Für kleine Stichproben mit s nimmst du die kritischen t-Werte.

Ergänzungen und Korrekturen

Die Korrektur für endliche Populationen (FPC) wird nötig, wenn man mehr als 5 % einer endlichen Grundgesamtheit untersucht:

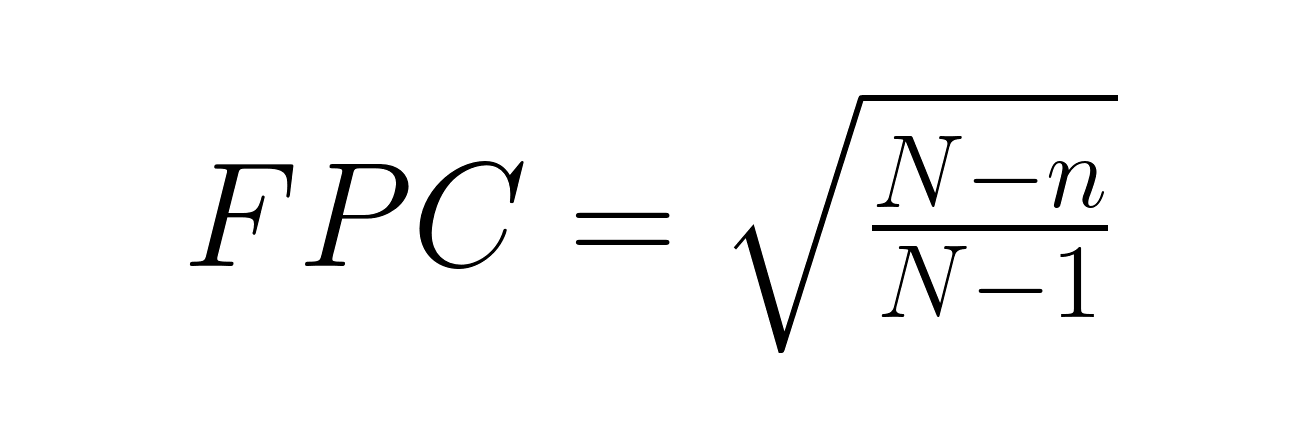
Wo:

• N = Gesamtbevölkerungsgröße
• n = Stichprobengröße

Der korrigierte Standardfehler wird zu:

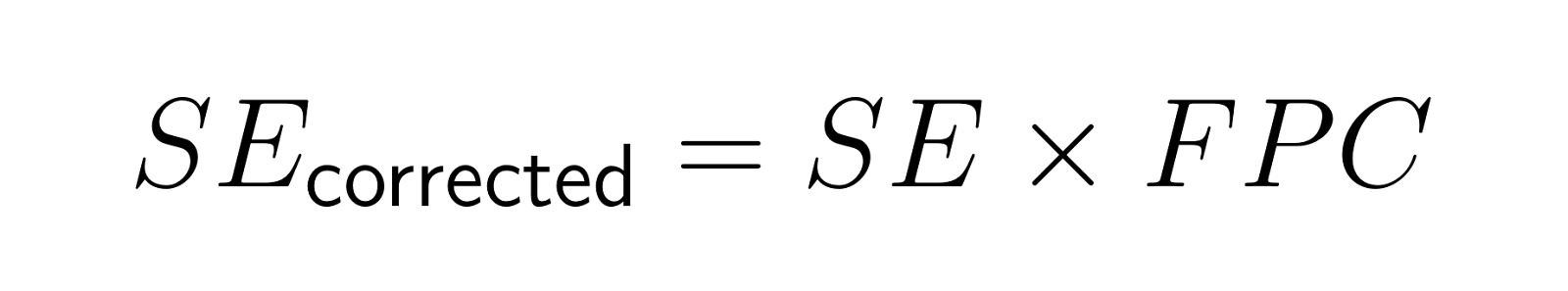
Wenn man zum Beispiel 200 Leute aus einer Stadt mit 2.000 Einwohnern befragt, kriegt man einen Korrekturfaktor von ungefähr 0,95, wodurch der Standardfehler um 5 % kleiner wird.

Gruppierte Proben müssen angepasst werden, weil die effektive Stichprobengröße durch den Designeffekt kleiner wird:

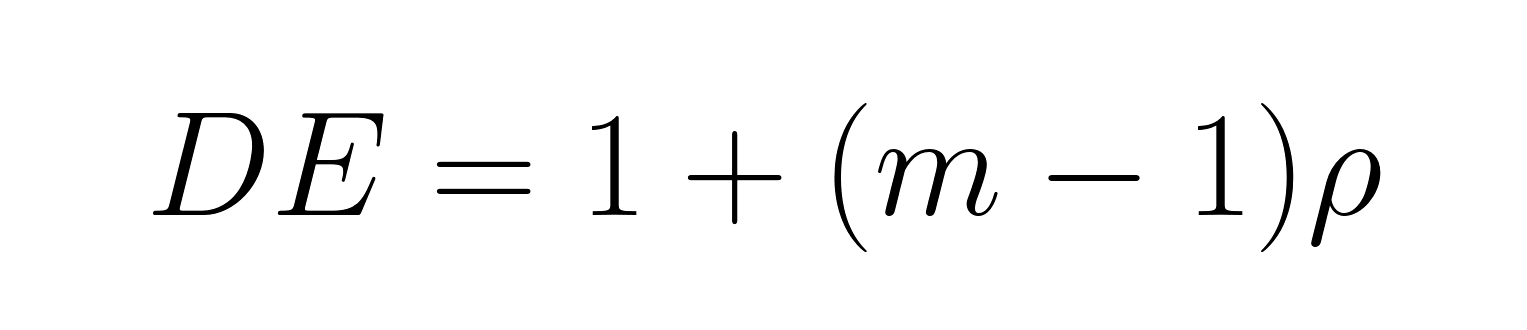
Wo:

• m = durchschnittliche Clustergröße
• ρ = Intracluster-Korrelationskoeffizient (wie ähnlich sich Beobachtungen innerhalb von Clustern sind)

Der angepasste Standardfehler wird zu:

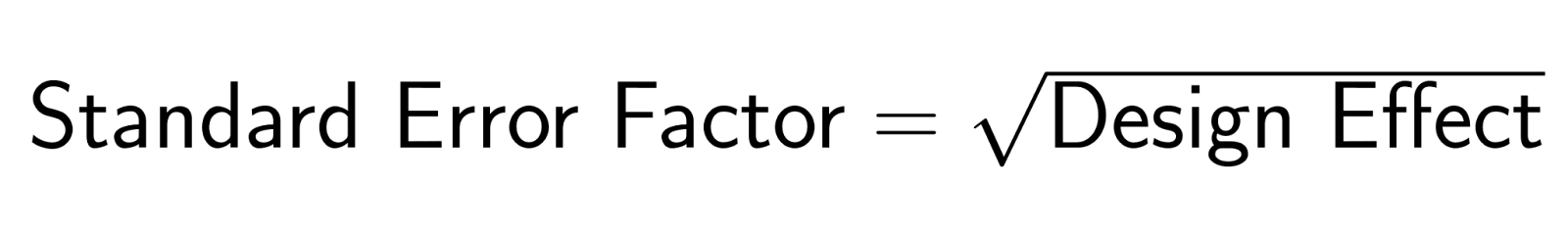
Wenn Familienmitglieder ähnliche Meinungen haben (ρ = 0,3) und die durchschnittliche Haushaltsgröße 3 beträgt, ist der Designeffekt DE = 1 + (3-1)(0,3) = 1,6. Der Standardfehlerfaktor ist √1,6 = 1,27, sodass die Standardfehler um 27 % größer sind als bei einer einfachen Zufallsstichprobe.

Anwendungen in der statistischen Inferenz

Der Standardfehler ist die Basis für einige der wichtigsten Techniken in der statistischen Inferenz, von Konfidenzintervallen bis hin zu Hypothesentests. Hier geht's darum, wie Standardfehler diese grundlegenden Verfahren möglich und zuverlässig machen.

Konfidenzintervallkonstruktion

Der Standardfehler bestimmt direkt das Konfidenzintervall :

Bei großen Stichproben liegt der kritische Wert bei einem Konfidenzniveau von 95 % bei ungefähr 1,96. Bei kleineren Stichproben werden kritische Werte der t-Verteilung verwendet, die ein bisschen größer sind. Diese Beziehung erklärt, warum Forscher oft neben Punktschätzungen auch Standardfehler angeben. Sie geben dir sofort einen Einblick in die Genauigkeit der Ergebnisse.

Enge Intervalle zeigen genaue Schätzungen mit kleinen Standardfehlern an, während breite Intervalle auf erhebliche Unsicherheit hindeuten. Das Konfidenzniveau (95 %, 99 % usw.) zeigt, wie sicher wir sein wollen, aber die Breite des Intervalls hängt stark vom Standardfehler ab.

Rahmen für Hypothesentests

Der Standardfehler macht Teststatistiken einheitlich, indem er die rohen Unterschiede in Einheiten der Stichprobenvariabilität umwandelt:

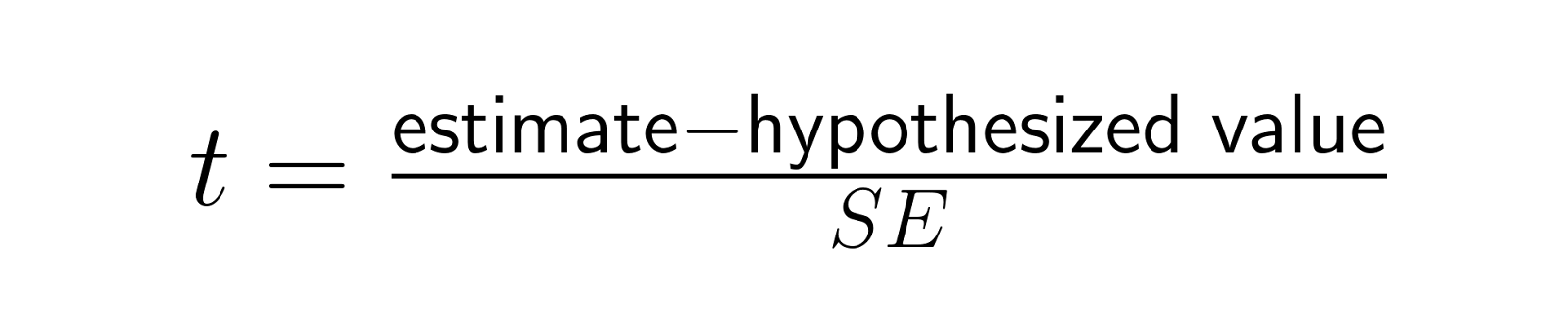
Diese t-Statistik macht es möglich, verschiedene Studien und Effektgrößen sinnvoll zu vergleichen, indem sie die Unterschiede im Verhältnis zu ihrer erwarteten Variabilität unter der Nullhypothese ausdrückt. Ein Unterschied von 5 Punkten kann bei SE = 1 (was t = 5 ergibt) echt wichtig sein, bei SE = 10 (was t = 0,5 ergibt) aber nicht so sehr. Das zeigt, wie der Standardfehler den Rahmen für die Interpretation von Effektgrößen gibt.

Da statistische Tests den beobachteten Effekt durch den Standardfehler teilen, führen kleinere Standardfehler dazu, dass selbst bescheidene reale Effekte statistische Signifikanz erreichen, während größere Standardfehler größere Effekte erfordern, um Signifikanz zu erreichen. Das erklärt, warum große Studien kleine, aber echte Effekte erkennen können, die kleinere Studien übersehen würden.

Meta-analytische Anwendungen

Bei der Metaanalyse bestimmt der Standardfehler, wie viel Gewicht jede Studie durch inverse Varianzgewichtung bekommt:

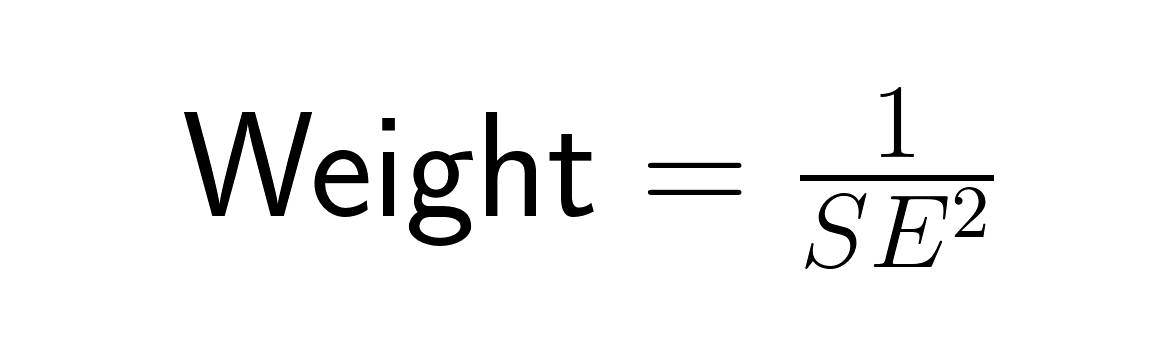
Studien mit kleineren Standardfehlern (genauere Schätzungen) werden stärker gewichtet als Studien mit größeren Standardfehlern, weil genauere Schätzungen mehr zu unserem Gesamtverständnis beitragen sollten. Eine Studie mit einem Standardfehler von 0,5 bekommt viermal so viel Gewicht wie eine Studie mit einem Standardfehler von 1,0. So werden die Infos aus den Studien optimal kombiniert, um den Gesamtstandardfehler der metaanalytischen Schätzung zu minimieren.

Standardfehler melden und interpretieren

Um Standardfehler klar zu erklären, muss man sowohl auf das Format der Darstellung als auch auf den Kontext achten, in dem sie interpretiert wird. Hier sind ein paar praktische Tipps, wie du Standardfehlerergebnisse richtig präsentierst und häufige Interpretationsfehler vermeidest. 

Tipps für die Berichterstattung

Sag immer, welche Art von Standardfehler du meldest, und halte dich dabei an ein einheitliches Format. Benutz Formate wie „Mittelwert (SE)“, z. B. „45,2 (2,8)“ in Tabellen. Bei Grafiken solltest du Fehlerbalken verwenden, die sich um eine Standardabweichung über und unter den Punktschätzungen erstrecken, aber klar sagen, ob die Fehlerbalken die Standardabweichung, die Standardabweichung oder die Konfidenzintervalle darstellen.

Interpretation in Regression und Modellen

Die Regressionsausgabe zeigt Standardfehler neben den Koeffizientenschätzungen an. Ein Koeffizient von 0,75 mit SE = 0,25 deutet darauf hin, dass der wahre Effekt wahrscheinlich zwischen etwa 0,25 und 1,25 liegt, während die t-Statistik von 3,0 starke Hinweise gegen die Nullhypothese liefert.

Überlegungen zu Nicht-Stichprobenfehlern

Der Standardfehler misst nur die Schwankungen in der Stichprobe. Es berücksichtigt keine Messfehler, Verzerrungen durch Nichtbeantwortung oder andere Unsicherheitsfaktoren. Systematische Verzerrungen wie Auswahlverzerrungen oder Störfaktoren können zu ungenauen Schätzungen führen, egal wie klein der Standardfehler ist. Lass dich nicht von kleinen Standardfehlern dazu verleiten, den Ergebnissen zu viel zu trauen, die vielleicht trotzdem systematisch verzerrt sind.

Häufige Missverständnisse und Fallstricke

Um Standardfehler richtig zu verstehen, muss man sich der häufigen Missverständnisse bewusst sein, die zu falschen Schlussfolgerungen führen können. Dieser Abschnitt geht auf die häufigsten Ursachen für Verwirrung ein und gibt Tipps, wie man Interpretationsfehler vermeiden kann.

Standardfehler vs. Standardabweichung

Standardfehler und Standardabweichung messen verschiedene Aspekte der Variabilität und sollten nicht verwechselt werden, auch wenn das in Forschungsberichten und in den Medien oft passiert. Die Standardabweichung zeigt, wie weit die einzelnen Werte vom Mittelwert der Stichprobe entfernt sind, und beantwortet die Frage: „Wie stark weichen die einzelnen Datenpunkte vom Durchschnitt ab?“ Der Standardfehler zeigt, wie genau der Stichprobenmittelwert als Schätzung des Populationsmittelwerts ist, und beantwortet die Frage: „Wie stark würden die Stichprobenmittelwerte variieren, wenn wir die Studie wiederholen würden?“

Die mathematische Beziehung hilft, den Unterschied zu verdeutlichen:

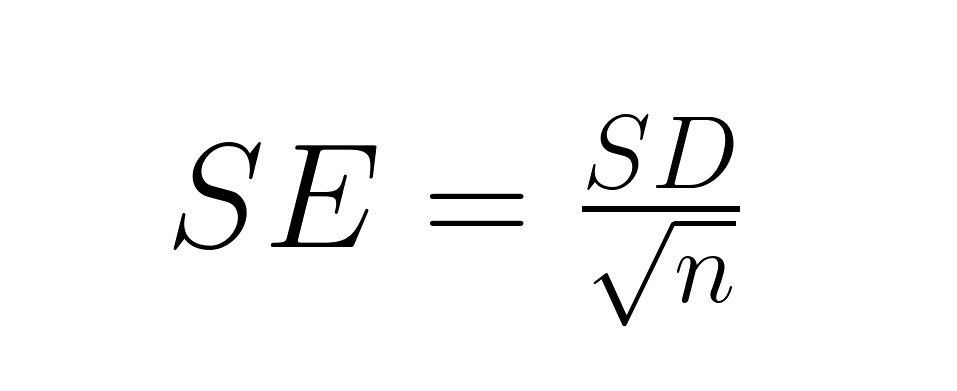
Der Standardfehler ist die Standardabweichung geteilt durch die Quadratwurzel der Stichprobengröße, also ist der Standardfehler immer kleiner als die Standardabweichung (außer wenn n = 1). Ein Datensatz mit Körpergrößen von Erwachsenen könnte eine Standardabweichung von 4 Zoll haben (was bedeutet, dass die Körpergrößen der einzelnen Personen ziemlich unterschiedlich sind), aber einen Standardfehler von 0,1 Zoll für den Stichprobenmittelwert (was auf eine ziemlich genaue Schätzung der durchschnittlichen Körpergröße hindeutet). 

Präzision vs. Genauigkeit – Missverständnisse

Der Standardfehler misst die Präzision, nicht die Genauigkeit. Ein kleiner Standardfehler zeigt, dass die Genauigkeit hoch ist, weil wiederholte Proben ähnliche Schätzungen ergeben würden, aber die Genauigkeit kann durch systematische Verzerrungen beeinträchtigt werden.

Stell dir eine Personenwaage vor, die immer 5 Pfund zu viel anzeigt: Wenn du dich 100 Mal wiegen würdest, bekämst du zwar super genaue Messungen (kleiner Standardfehler), aber immer ungenaue Ergebnisse. Ein niedriger Standardfehler garantiert keine korrekten Ergebnisse.

Nachteile und Einschränkungen

Bei Standardfehlerberechnungen geht man von zufälligen Stichproben, unabhängigen Beobachtungen und oft auch Normalität aus. Bei nicht zufälligen Stichproben ist der Standardfehler nicht richtig, während korrelierte Beobachtungen (wie Schüler innerhalb von Schulen) größere Standardfehler brauchen.

Nimm einen niedrigen Standardfehler nicht als „Beweis“ für ein Ergebnis. Eine randomisierte kontrollierte Studie mit geringem Standardfehler liefert überzeugendere Beweise als eine Beobachtungsstudie mit ebenso geringem Standardfehler, weil das Studiendesign die Validität beeinflusst, unabhängig von der statistischen Genauigkeit. Unser Experimentelles Design in R behandelt die Prinzipien der richtigen Randomisierung, Blockbildung und experimentellen Kontrolle, die sicherstellen, dass Ihre Standardfehlerberechnungen zu validen Schlussfolgerungen führen.

Fortgeschrittene methodische Erweiterungen

Die moderne Statistik hat Alternativen und Erweiterungen zu den klassischen Standardfehleransätzen entwickelt, die Lösungen bieten, wenn traditionelle Methoden nicht ausreichen oder wenn eine komplexere Quantifizierung der Unsicherheit nötig ist.

Bootstrapping-Techniken bieten einen nichtparametrischen Ansatz, der nicht auf Verteilungsannahmen basiert. Durch wiederholtes Resampling der Originaldaten schätzen Bootstrap-Methoden Standardfehler für komplexe Statistiken, für die es keine analytischen Formeln gibt. Unsere Kurs „Sampling in Python” behandelt Bootstrap-Techniken.

Robuste Standardfehler berücksichtigen Annahmenverletzungen. Heteroskedastizitätskonsistente Standardfehler bleiben auch dann gültig, wenn die Restvarianz nicht konstant ist, während gruppierte Standardfehler die Korrelation innerhalb von Gruppen berücksichtigen. Diese Methoden führen normalerweise zu größeren Standardfehlern und liefern konservativere Schlussfolgerungen.

Bayesianische Ansätze quantifizieren Unsicherheit in der Statistik eher über A-posteriori-Verteilungen als über Standardfehler. Bayesianische Glaubwürdigkeitsintervalle liefern direkte Wahrscheinlichkeitsaussagen: „Es ist ziemlich sicher, dass der Wert zwischen 2,1 und 4,7 liegt.“ Schau dir unser Bayesianische Regressionsmodellierung mit rstanarm und lerne, wie Bayes'sche Methoden mit Unsicherheit anders umgehen.

Fazit

Der Standardfehler verbindet Stichprobendaten und Populationsschätzungen, quantifiziert die Genauigkeit unserer Schätzungen und ermöglicht aussagekräftige statistische Schlussfolgerungen. Die wichtigste Erkenntnis: Der Standardfehler misst die Präzision, nicht die Genauigkeit. Es zeigt uns, wie konsistent unsere Schätzungen bei wiederholten Stichproben wären, nicht aber, ob diese Schätzungen richtig sind.

Benutz Standardfehler richtig, indem du die Annahmen überprüfst, den richtigen Typ auswählst und die Ergebnisse im größeren Kontext des Studiendesigns interpretierst. Gib immer Standardfehler zusammen mit Punktschätzungen an, sag, welche Art du benutzt, und sei dir der Einschränkungen bewusst. Schau dir doch mal fortgeschrittene Methoden in unserem Kurs „Statistische Inferenz in R” an. Statistische Inferenz in R, um einen tieferen Lernpfad zu gehen.

Egal, ob du Experimente planst, Umfragedaten analysierst oder Forschungsergebnisse interpretierst – der Standardfehler ist die Basis für eine ehrliche Quantifizierung der Unsicherheit, die Vertrauen in statistische Ergebnisse schafft.