Cours
Si nous prélevons un grand nombre d'échantillons aléatoires à partir d'à peu près n'importe quel type de distribution de données, il se produit quelque chose de surprenant. La moyenne de ces échantillons commence à ressembler à une distribution normale - cette courbe familière en forme de cloche. C'est le théorème de la limite centrale (CLT) en bref.
Il s'agit d'un aspect important des probabilités et des statistiques, car cela signifie que nous pouvons faire des prédictions précises et tirer des conclusions sur des populations entières, même si nous n'examinons que de petits échantillons.
Ce qui rend le CLT particulièrement utile, c'est qu'il fonctionne même si les données originales ne sont pas normalement distribuées. Examinons cela en détail et voyons comment nous pouvons le calculer.
Qu'est-ce que le théorème de la limite centrale ?
Le théorème de la limite centrale, ou CLT, est une idée de statistique selon laquelle si l'on prend un ensemble d'échantillons aléatoires d'une population et que l'on examine les moyennes de ces échantillons, ces moyennes commenceront à former une courbe normale, en forme de cloche, même si la population d'origine ne semble pas normale du tout.
Ceci est lié à la loi des grands nombres, qui nous dit qu'au fur et à mesure que nous collectons des données, la moyenne de notre échantillon se rapproche de plus en plus de la moyenne réelle de l'ensemble de la population. Le CLT va plus loin : il nous dit que la moyenne de l'échantillon devient plus précise et que le modèle de ces moyennes devient prévisible. Notre cours d' introduction aux statistiques propose des exercices pratiques pour vous familiariser avec la relation et les différences entre la CLT et la loi des grands nombres, si vous souhaitez approfondir cette partie.
Un bon moyen d'illustrer ce principe est de lancer un dé. Si nous le lançons une seule fois, nous obtenons un nombre aléatoire compris entre 1 et 6. Mais après un nombre suffisant de lancers, la moyenne s'établira autour de 3,5 (la vraie valeur moyenne d'un dé juste). Faites-le de manière répétée et la distribution de ces moyennes commence à ressembler à une courbe normale.
Formule du théorème de la limite centrale
Voici la formule de base du théorème de la limite centrale :
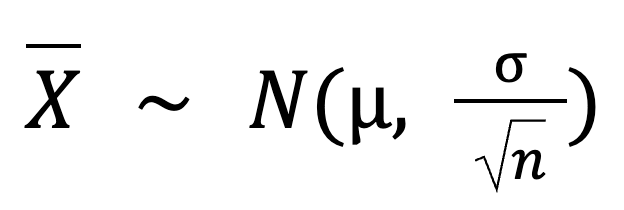
Dans cette formule :
-
Xest la distribution d'échantillonnage de la moyenne de l'échantillon, qui suit une distribution normale. -
Nest la distribution normale. -
𝜇est la moyenne de la population. -
σest l'écart-type de la population. -
nest la taille de l'échantillon.
Plus la taille de l'échantillon est importante, plus l'écart-type de la distribution d'échantillonnage diminue. Plus nous collectons de données, plus les moyennes de nos échantillons seront étroitement groupées autour de la véritable moyenne de la population.
Conditions du théorème de la limite centrale
Pour que le théorème de la limite centrale fonctionne comme nous l'attendons, il y a quelques conditions à prendre en compte :
- Taille de l'échantillon suffisamment importante : La taille de l'échantillon doit être suffisante. Un échantillon de 30 personnes ou plus est généralement considéré comme bon. Mais si la population que nous échantillonnons est asymétrique ou comporte de nombreuses valeurs aberrantes, il se peut que nous ayons besoin d'un échantillon plus important pour voir apparaître cette belle courbe en forme de cloche.
- Échantillons indépendants et identiquement distribués (i.i.d.) : Les échantillons que nous prélevons doivent être indépendants et identiquement distribués (i.i.d.). Cela signifie que chaque échantillon est choisi au hasard et provient de la même population. Si ce n'est pas le cas, les résultats peuvent ne pas être fiables.
- Variance de population finie: La population que nous échantillonnons doit avoir une variance finie. Si les données proviennent d'une distribution à variance infinie, comme la distribution de Cauchy, le CLT ne s'appliquera pas à ces données.
Exemples de théorème de la limite centrale
Supposons que nous voulions savoir combien de tasses de café sont vendues par jour dans un café local. Au fil des ans, le nombre de gobelets vendus chaque jour peut suivre une distribution similaire à celle que j'ai incluse ici. La plupart du temps, ils vendent entre 80 et 120 tasses. Mais les jours de grande affluence, comme les jours fériés ou les événements spéciaux, ils vendent 150, voire 180 gobelets. Dans ce cas, les données sont quelque peu asymétriques (inégales).
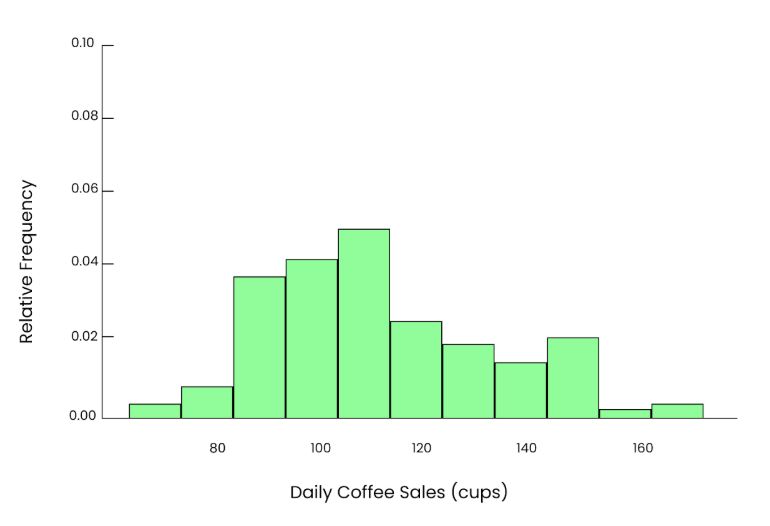
Graphique irrégulier. Image par l'auteur.
Supposons que nous prenions un petit échantillon. Nous choisissons au hasard 5 jours dans l'année et nous regardons combien de gobelets ont été vendus ces jours-là.
95, 102, 85, 110, 120La moyenne obtenue à partir de cet échantillon est la suivante :
Mean = 95+102+85+110+1205 = 102.4 cups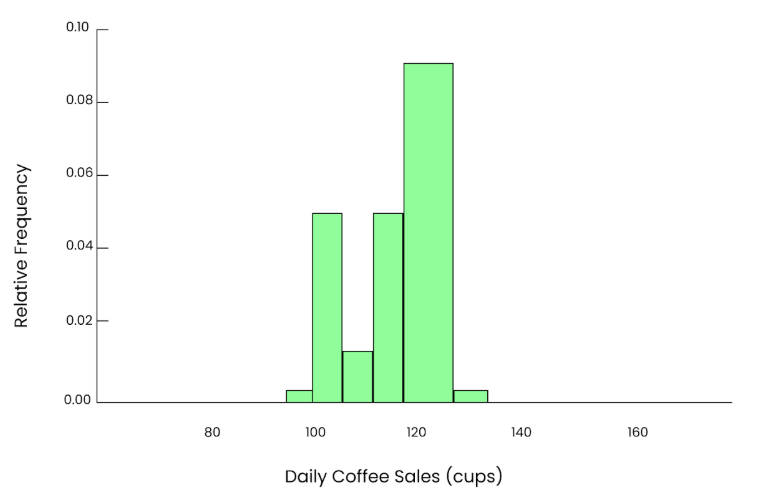
Graphique de 5 tasses. Image par l'auteur.
Cela nous donne une estimation de la moyenne de la population, mais comme l'échantillon est petit, il se peut qu'elle ne soit pas exacte. Si nous répétons ce processus 10 fois, choisissons au hasard 5 jours à chaque fois, calculons la moyenne et notons les résultats. Les moyennes des 10 échantillons seraient les suivantes :
97.6, 105.8, 93.4, 110.2, 99.0, 102.4, 101.2, 107.5, 96.3, 94.1Si nous représentons ces valeurs dans un histogramme, nous verrons une forme de cloche approximative, mais elle peut encore sembler inégale. Et la dispersion de ces moyens est plus faible que la dispersion dans la population.
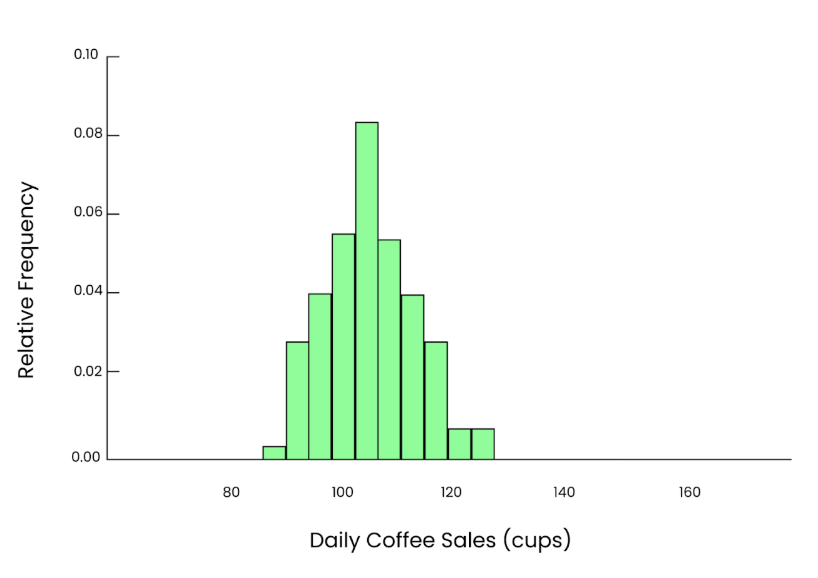
Graphique de 10 tasses. Image par l'auteur.
Prenons maintenant un échantillon plus important. Cette fois, nous choisissons au hasard 50 jours et calculons le nombre moyen de gobelets vendus :
98, 104, 87, 112, 105, 100, 108, 95, 102, 106,
92, 115, 97, 101, 109, 103, 96, 110, 104, 98,
100, 102, 89, 107, 94, 111, 108, 90, 100, 103,
106, 99, 96, 112, 105, 97, 100, 104, 93, 110,
107, 102, 95, 101, 99, 103, 109, 98, 94, 100Lorsque nous calculons la moyenne de cet échantillon, nous obtenons :
Mean = 101.2 cupsCette estimation est beaucoup plus proche de la moyenne de la population (100) et, comme notre échantillon est plus grand, elle est plus précise.
Si nous répétons ce processus plusieurs fois, en choisissant à chaque fois 50 jours au hasard, en calculant la moyenne et en représentant ces moyennes dans un histogramme, même si les données d'origine étaient asymétriques, nous verrons une courbe en forme de cloche apparente et lisse. C'est là toute la puissance du théorème de la limite centrale.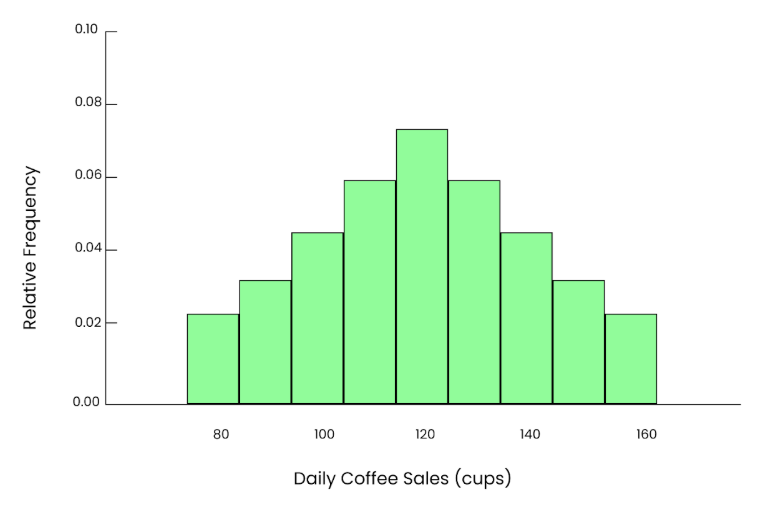
Même graphique. Image par l'auteur.
Nous pouvons même calculer cet écart à l'aide de cette formule :
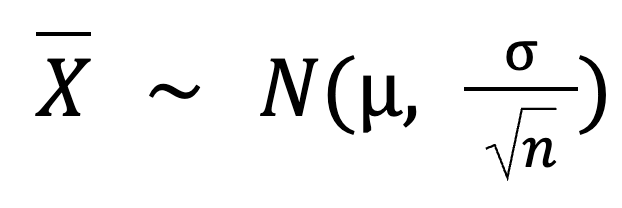 Ici :
Ici :
-
µ(moyenne de la population) = 100 -
σ(écart-type de la population) = 15 -
n(taille de l'échantillon) = 50
Ainsi, l'écart-type des moyennes de notre échantillon est :
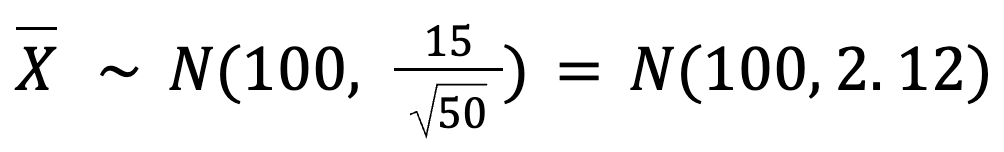
Cela nous indique que les moyennes de l'échantillon seront très proches de 100 tasses avec juste une petite variation (environ 2,12 tasses).
L'importance du théorème de la limite centrale
Nous savons maintenant que les données dans le monde réel peuvent être bizarres et imprévisibles. Mais le théorème central limite nous offre un moyen fiable de comprendre ce qui se passe et de faire de meilleurs choix en conséquence. Comprenons son importance plus en détail.
Inférence statistique
En statistique, le théorème de la limite centrale est la raison pour laquelle les tests paramétriques tels que les tests t, l'ANOVA et la régression fonctionnent comme ils le font. Ces tests reposent sur l'idée que les données d'un échantillon proviennent d'une population aux caractéristiques fixes.
Sans le théorème de la limite centrale, nous ne pourrions pas nous fier à ces tests. En raison de ce théorème, les tests paramétriques sont souvent plus puissants que les tests non paramétriques, qui ne font pas d'hypothèses sur la distribution des données.
Applications industrielles
On le retrouve également dans de nombreuses situations du monde réel. En finance, les analystes l'utilisent pour estimer les rendements moyens des actions sur la base des performances passées. Dans les sondages et les enquêtes, elle permet de faire des prévisions sur l'ensemble de la population en recueillant un échantillon de réponses. Dans le domaine de l'apprentissage automatique et du big data, nous l'utilisons lorsque les modèles sont formés sur des échantillons. Par exemple, une application de cinéma peut utiliser un échantillon de l'activité des utilisateurs pour construire son système de recommandation.
Calculatrice du théorème de la limite centrale
L'écart-type est un chiffre qui nous indique à quel point les valeurs s'écartent de la moyenne. Lorsque nous examinons les moyennes d'un échantillon (les moyennes de différents échantillons), nous voulons savoir dans quelle mesure ces moyennes varient. Pour cela, nous pouvons utiliser la formule suivante :
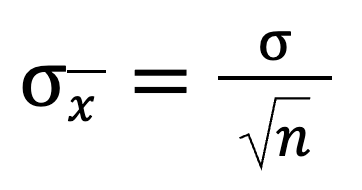
Cela signifie qu'en divisant l'écart-type de la population par la racine carrée de la taille de l'échantillon, on obtient l'écart-type de la distribution d'échantillonnage. Plus la taille de l'échantillon est importante, plus la valeur globale diminue.
Prenons un exemple rapide :
| Taille de l'échantillon (n) | Moyenne de l'échantillon (μₓ̄) | Std. Écart (σₓ̄) |
|---|---|---|
| 5 | 17 | 1.788854 |
| 10 | 17 | 1.264911 |
| 25 | 17 | 0.800000 |
| 50 | 17 | 0.565685 |
| 100 | 17 | 0.400000 |
Vous pouvez constater que la moyenne reste inchangée, mais que l'écart-type continue de diminuer. Cela montre que plus l'échantillon est grand, plus il est précis et cohérent.
Le théorème de la limite centrale dans la science des données
En science des données, nous traitons généralement des échantillons, et non des populations entières. Le CLT nous aide à comprendre le comportement des résultats de ces échantillons et nous indique que si nous prenons suffisamment d'échantillons, leurs moyennes commenceront à ressembler à une distribution normale, même si les données d'origine sont tout sauf normales.
Cela présente également des avantages importants dans le monde réel. Dans le domaine de l'apprentissage automatique, nous utilisons souvent des techniques telles que le bootstrapping pour estimer les valeurs. Grâce au CLT, nous pouvons être sûrs que ces estimations sont exactes.
C'est également un acteur clé des tests A/B. Lorsqu'une entreprise teste deux versions d'une page web ou d'une fonctionnalité, le CLT nous aide à déterminer si les résultats sont significatifs ou s'il s'agit d'un bruit aléatoire.
Même dans le cas de l'apprentissage par renforcement, où les systèmes apprennent par essais et erreurs, la CLT aplanit le chaos. Au fur et à mesure que les données affluent, les moyennes deviennent plus stables, ce qui permet au système d'apprendre plus vite et mieux.
Enfin, vous verrez également le CLT dans les tests d'hypothèse et l'analyse des séries temporelles. Il aide les data scientists à tester des idées et à suivre des tendances avec plus de confiance.
Réflexions finales
Le théorème central limite peut sembler technique si vous ne connaissez pas les statistiques, mais c'est en grande partie grâce à lui que nous pouvons faire des choses intelligentes avec les données. Il transforme le hasard en quelque chose que nous pouvons comprendre et en quoi nous pouvons avoir confiance. En fait, il s'agit de l'un des éléments constitutifs de la modélisation statistique et d'une connaissance indispensable pour quiconque travaille avec des données.
Si vous voulez en savoir plus, lisez la loi des grands nombres et les distributions de probabilités - tout cela est lié.
Je suis un stratège du contenu qui aime simplifier les sujets complexes. J'ai aidé des entreprises comme Splunk, Hackernoon et Tiiny Host à créer un contenu attrayant et informatif pour leur public.
FAQ sur le théorème de la limite centrale
Le théorème de la limite centrale peut-il être utilisé avec des données non numériques ?
Oui, mais pas directement. Le CLT s'applique aux données numériques, en particulier aux moyennes et aux sommes. Cependant, pour les données catégorielles ou ordinales, vous pouvez toujours utiliser des principes similaires en convertissant les données sous forme numérique ou en utilisant d'autres techniques statistiques.
Quelle est la différence entre la distribution d'un échantillon et la distribution d'une population ?
La distribution de la population décrit l'ensemble des données, tandis que la distribution d'échantillonnage fait référence à la distribution des statistiques de l'échantillon (comme les moyennes) à partir d'un échantillonnage répété.
Comment les valeurs aberrantes affectent-elles le théorème de la limite centrale ?
Les valeurs aberrantes augmentent l'asymétrie et la variance, ce qui signifie qu'il peut être nécessaire d'augmenter la taille de l'échantillon pour que la distribution d'échantillonnage se rapproche de la normalité.
