¿Qué es el error estándar? La clave para la precisión y la confianza estadísticas

Cuando un investigador médico afirma que un nuevo medicamento reduce la presión arterial en una media de 15 puntos, ¿qué grado de confianza debemos tener en esa afirmación? La respuesta suele estar en comprender el error estándar, que es una medida estadística que nos indica cuán precisas son realmente nuestras estimaciones muestrales.

William Sealy Gosset, que escribía bajo el seudónimo de «Student» mientras trabajaba en la fábrica de cerveza Guinness, desarrolló la teoría de las muestras pequeñas a partir de retos reales relacionados con la elaboración de cerveza. Su trabajo nos proporcionó las bases matemáticas para realizar inferencias sólidas cuando no conocemos los parámetros reales de la población.

Esta guía presenta los conceptos clave, las fórmulas matemáticas y las aplicaciones prácticas del error estándar en diferentes contextos estadísticos. Nuestro Muestreo en R cubre los principios detrás de estos cálculos con más detalle, y la comprensión de cómo el error estándar se relaciona con desviación estándar muestral te proporciona una base sólida para la inferencia estadística.

¿Qué es el error estándar?

El error estándar proporciona una medida de la incertidumbre en torno a las estadísticas muestrales, lo que nos ayuda a comprender en qué medida podrían variar nuestras estimaciones si repitiéramos el mismo estudio varias veces. Examinamos el concepto básico y exploramos las diferentes formas que adopta el error estándar en diversos análisis estadísticos.

Concepto básico e intuición

El error estándar mide la variabilidad de una estadística muestral en muestras repetidas de la misma población. Piensa en ello como si respondieras: «Si recogiera 100 muestras diferentes del mismo tamaño, ¿cuánto variarían las medias de mis muestras?».

Este concepto surge directamente de la teoría de la distribución muestral. Cuando calculamos la media de una muestra, ese valor representa solo uno de los posibles resultados de muchas muestras potenciales. El error estándar cuantifica la distancia típica entre cualquier estadística muestral individual y el parámetro poblacional real que estamos tratando de estimar.

El error estándar mide la precisión con la que una estadística muestral estima un parámetro poblacional. Un error estándar más pequeño significa que muestras repetidas producirían estimaciones similares, lo que sugiere que nuestra muestra actual proporciona una aproximación fiable. Un error estándar mayor sugiere una variabilidad sustancial entre las muestras potenciales, lo que indica una menor confianza en nuestra estimación.

Múltiples tipos de error estándar

No hay un único error estándar. Las diferentes estadísticas requieren fórmulas especializadas propias en función de lo que estemos midiendo. Los tipos más comunes incluyen:

• Error estándar de la media: Se utiliza para estimar los promedios de población.
• Error estándar de una proporción: Aplicado a estimaciones de porcentajes o tasas
• Error estándar de la diferencia entre medias: Se utiliza cuando se comparan dos grupos.
• Error estándar de los coeficientes de regresión: Aplicado a estimaciones de pendiente en modelos lineales.

Cada tipo tiene fines analíticos específicos y aborda diferentes fuentes de variabilidad. Por ejemplo, el error estándar de una proporción tiene en cuenta la naturaleza binomial de las respuestas sí/no, mientras que el error estándar de una pendiente de regresión considera tanto la variación residual como la dispersión de los valores predictivos.

Es importante elegir el tipo adecuado. El uso de una fórmula incorrecta puede llevar a conclusiones excesivamente optimistas o a pasar por alto efectos importantes.

Fundamentos conceptuales del error estándar

En esta sección se analiza cómo el error estándar se basa en la teoría del muestreo y el razonamiento estadístico, lo que proporciona la base teórica que hace que los cálculos del error estándar sean significativos y fiables.

Teoría de la distribución muestral

El concepto de distribución muestral proporciona la base teórica para el error estándar. Si pudiéramos recopilar todas las muestras posibles de tamaño n de una población y calcular la estadística de interés para cada muestra, crearíamos una distribución muestral. El error estándar es igual a la desviación estándar de esta distribución muestral teórica, lo que explica por qué cuantifica cuánto varían las estadísticas muestrales individuales en torno al parámetro poblacional real.

El tamaño de la muestra tiene una relación inversa con el error estándar. A medida que aumenta el tamaño de la muestra, el error estándar disminuye proporcionalmente a la raíz cuadrada de n. El Teorema del Límite Central añade que las distribuciones muestrales se aproximan a la normalidad a medida que aumenta el tamaño de la muestra, independientemente de la distribución subyacente de la población. Esta suposición de normalidad nos permite construir intervalos de confianza y pruebas de hipótesis utilizando el error estándar, incluso con datos no normales, siempre que el tamaño de la muestra sea lo suficientemente grande.

Factores que influyen en la magnitud

Tres factores determinan la magnitud del error estándar: el tamaño de la muestra, la variabilidad de la población y el diseño del muestreo. La variabilidad de la población afecta directamente al error estándar. Las poblaciones más variables producen errores estándar mayores para cualquier tamaño de muestra dado. Una encuesta sobre los ingresos familiares en zonas urbanas con grandes disparidades económicas producirá errores estándar mayores que en comunidades rurales con ingresos homogéneos, incluso con muestras de idéntico tamaño.

El tamaño de la muestra proporciona la influencia más controlable a través de la relación inversa de la raíz cuadrada. Para reducir el error estándar a la mitad, es necesario cuadruplicar el tamaño de la muestra. El diseño del muestreo también es importante: el muestreo por conglomerados suele aumentar el error estándar, ya que las observaciones dentro de los conglomerados tienden a ser similares, mientras que el muestreo estratificado puede reducir el error estándar al garantizar la representación de los subgrupos importantes.

Error estándar, tamaño de la muestra y ley de los grandes números

La ley de los grandes números explica por qué el error estándar disminuye con muestras más grandes. Las estadísticas muestrales convergen hacia los parámetros poblacionales a medida que aumenta el tamaño de la muestra. El error estándar es proporcional a 1/√n. Por eso se necesitan muestras de gran tamaño para lograr mejoras sustanciales en la precisión. Cuadruplicar el tamaño de la muestra solo reduce a la mitad el error estándar.

Pero hay un inconveniente: aunque las muestras más grandes reducen el error estándar y aumentan la precisión, las muestras extremadamente grandes pueden producir resultados estadísticamente significativos para diferencias triviales que carecen de importancia práctica. Un estudio realizado con 100 000 personas podría detectar una diferencia de 0,1 puntos en la presión arterial que, aunque estadísticamente significativa, sería clínicamente irrelevante. Las muestras pequeñas pueden pasar por alto efectos importantes debido a los grandes errores estándar. Debes equilibrar la importancia estadística con la importancia práctica.

Formulación matemática y cálculo

Pasando de la comprensión conceptual a los procedimientos computacionales, las fórmulas matemáticas y los cálculos paso a paso hacen que el error estándar sea práctico para el análisis de datos.

Ecuaciones fundamentales para diferentes escenarios

La fórmula básica para el error estándar de la media depende de si se conoce la desviación estándar de la población. Cuando se conoce, utilizamos directamente el parámetro poblacional:

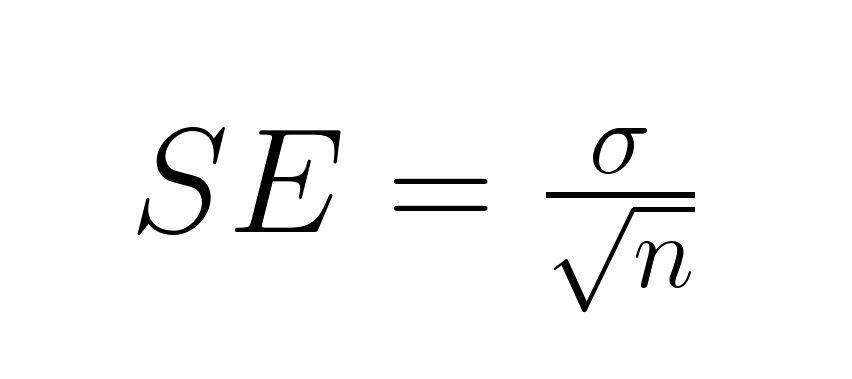
Dónde:

• σ = desviación estándar de la población
• n = tamaño de la muestra

Lo más habitual es que se desconozca la desviación estándar de la población, por lo que sustituimos la desviación estándar de la muestra, lo que introduce una incertidumbre adicional que requiere hacer referencia a la distribución t:

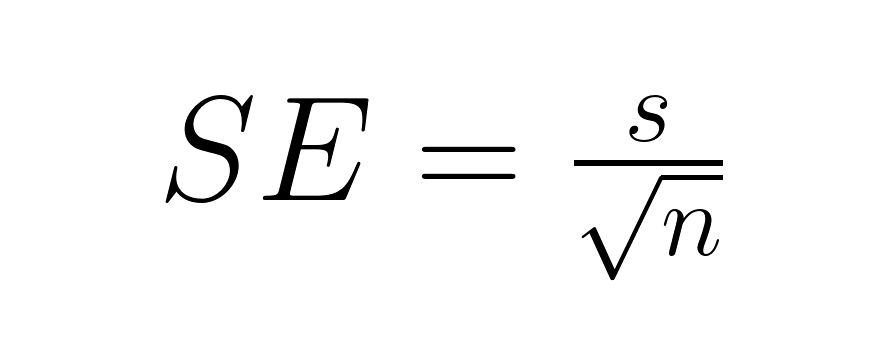
Dónde:

• s = desviación estándar de la muestra
• n = tamaño de la muestra

El error estándar de una proporción aborda los resultados binarios utilizando la fórmula de la distribución binomial:

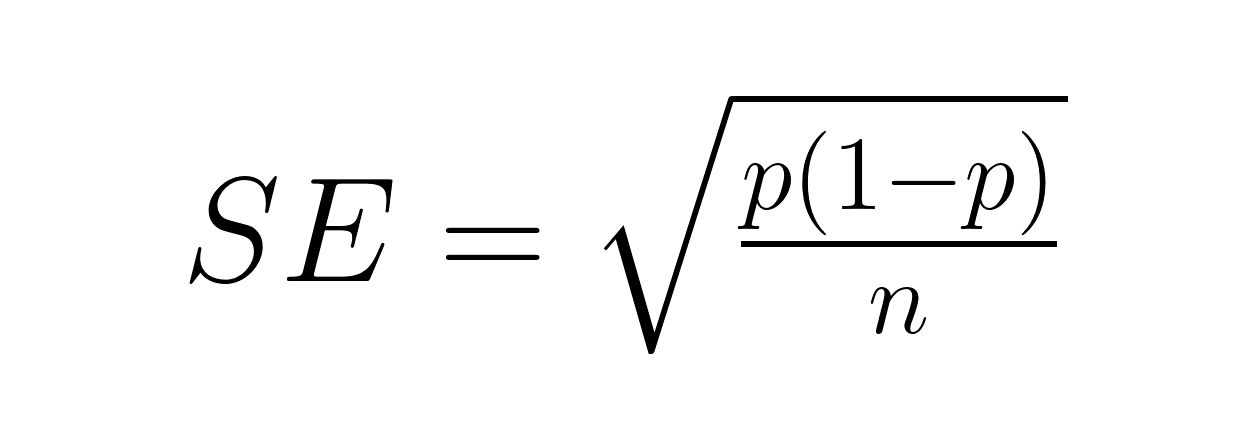
Dónde:

• p = proporción muestral
• n = tamaño de la muestra

El error estándar de una pendiente de regresión implica tanto la variación residual como la dispersión de la variable predictora:

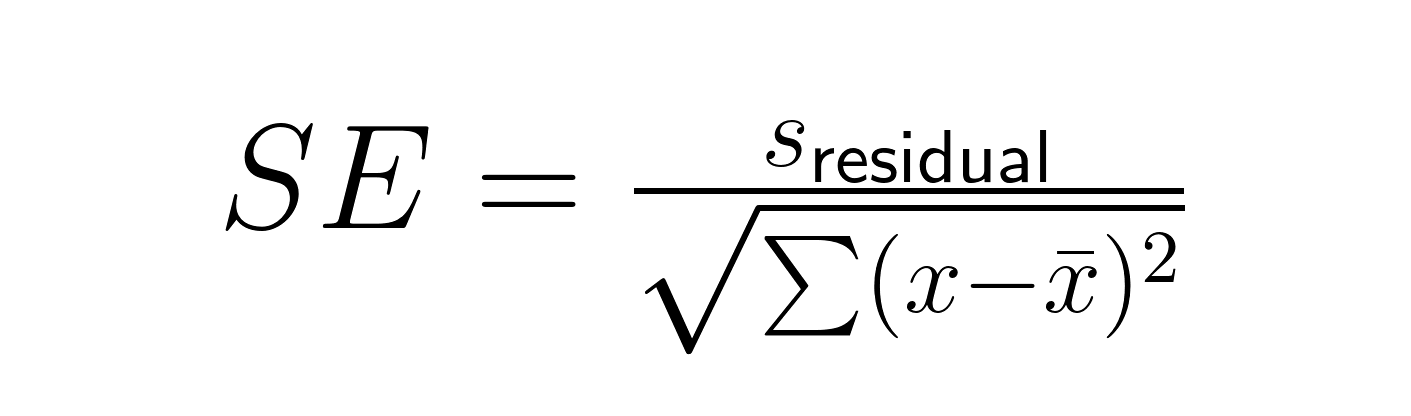
Dónde:

• sresidual = error estándar residual de la regresión
• x = valores predictivos individuales
• x̄ = media de los valores predictores

El error estándar de la diferencia entre medias varía dependiendo de si los grupos son independientes o emparejados. Para grupos independientes:

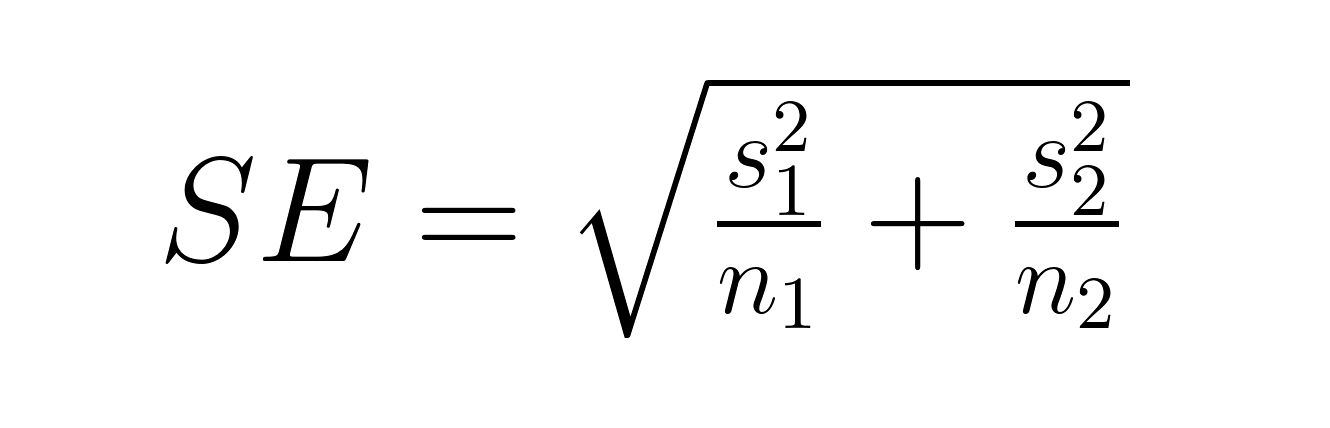
Dónde:

• s₁, s₂ = desviaciones estándar de los grupos 1 y 2
• n₁, n₂ = tamaños de muestra de los grupos 1 y 2

Para comparaciones por pares, la fórmula se simplifica considerablemente:

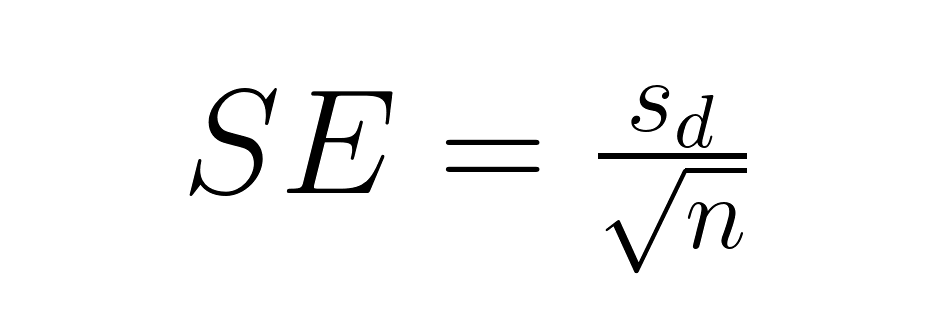
Dónde:

• sd = desviación estándar de las diferencias emparejadas
• n = número de pares

Procedimientos y escenarios de cálculo

Los parámetros poblacionales conocidos representan el escenario ideal que permite utilizar la distribución normal para la inferencia. Los parámetros desconocidos reflejan situaciones típicas de investigación en las que realizamos estimaciones a partir de datos muestrales mediante un proceso de tres pasos:

Paso 1: Calcula la media muestral. 

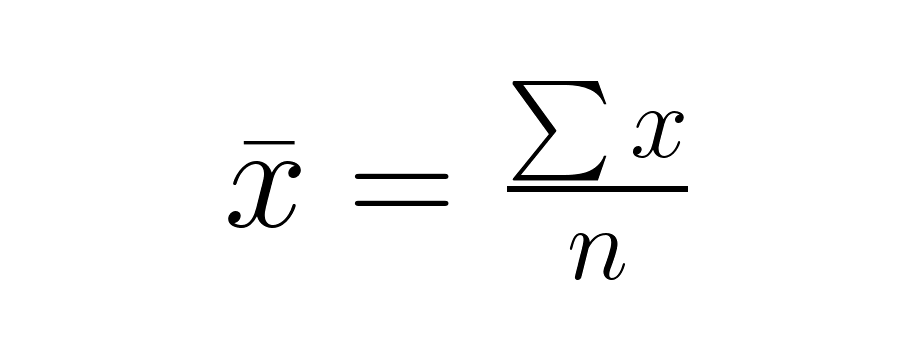
Paso 2: Calcula la desviación estándar de la muestra. 

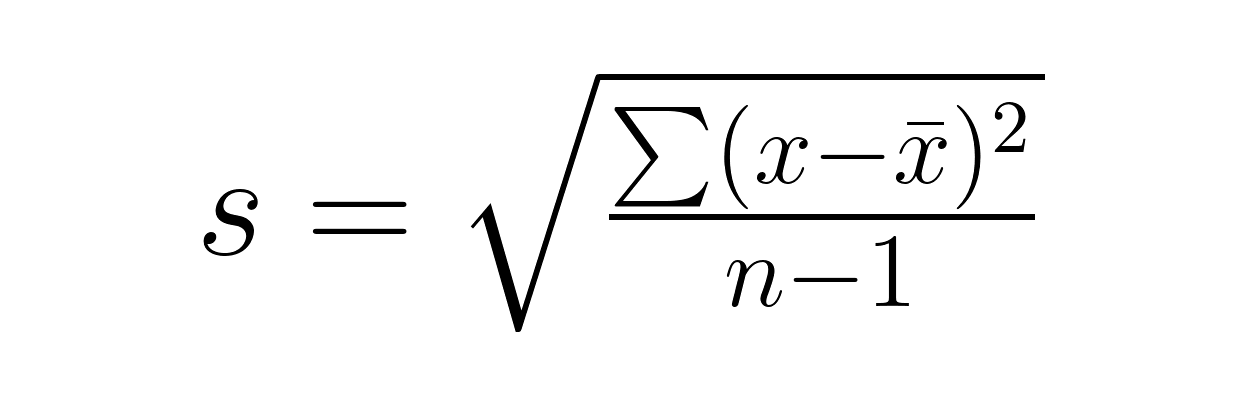
Paso 3: Aplica la fórmula de error estándar adecuada utilizando la desviación estándar de la muestra.

Interpretación: Los errores estándar más pequeños indican estimaciones más precisas. Un error estándar de 2,5 para una media muestral de 50 sugiere que la media real de la población probablemente se sitúe entre 45 y 55 aproximadamente, mientras que un error estándar de 10 indica una incertidumbre mucho mayor. En condiciones de normalidad aproximada, alrededor del 68 % se encuentra dentro de 1 DE y alrededor del 95 % dentro de 1,96 DE de la media real. Para muestras pequeñas que utilizan s, utiliza los valores críticos de t.

Ampliaciones y correcciones

La corrección por población finita (FPC) se hace necesaria cuando se muestrea más del 5 % de una población finita:

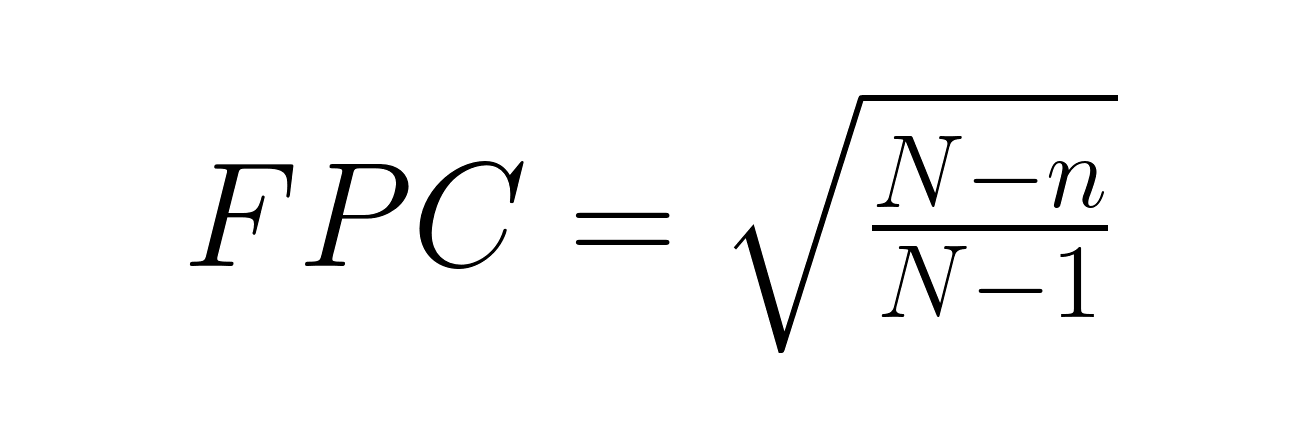
Dónde:

• N = tamaño total de la población
• n = tamaño de la muestra

El error estándar corregido pasa a ser:

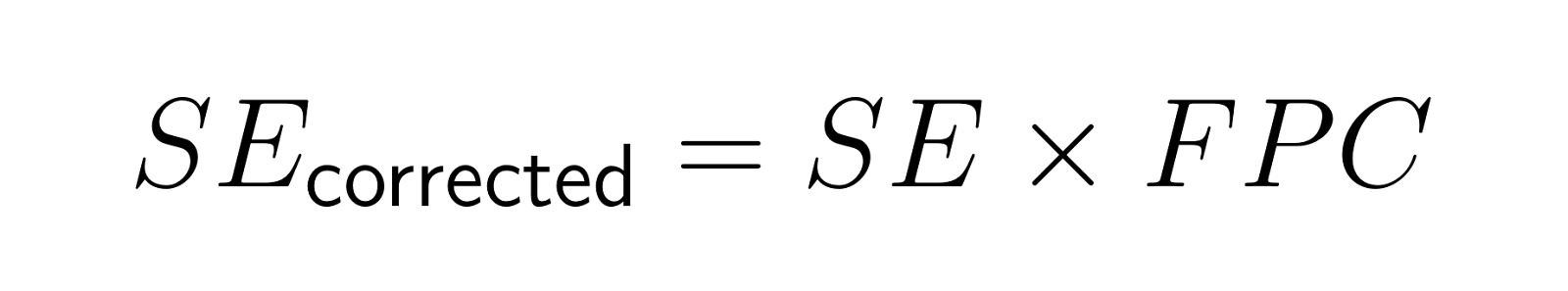
Por ejemplo, encuestar a 200 personas de una ciudad de 2000 habitantes da como resultado un factor de corrección de aproximadamente 0,95, lo que reduce el error estándar en un 5 %.

Las muestras agrupadas requieren ajustes para reducir el tamaño efectivo de la muestra utilizando el efecto del diseño:

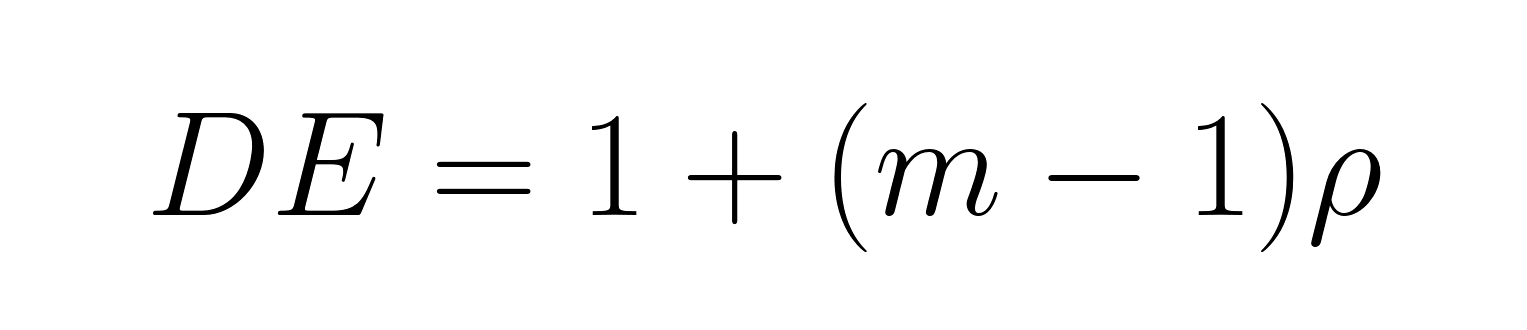
Dónde:

• m = tamaño medio del clúster
• ρ = coeficiente de correlación intraclúster (grado de similitud entre las observaciones dentro de los clústeres)

El error estándar ajustado se convierte en:

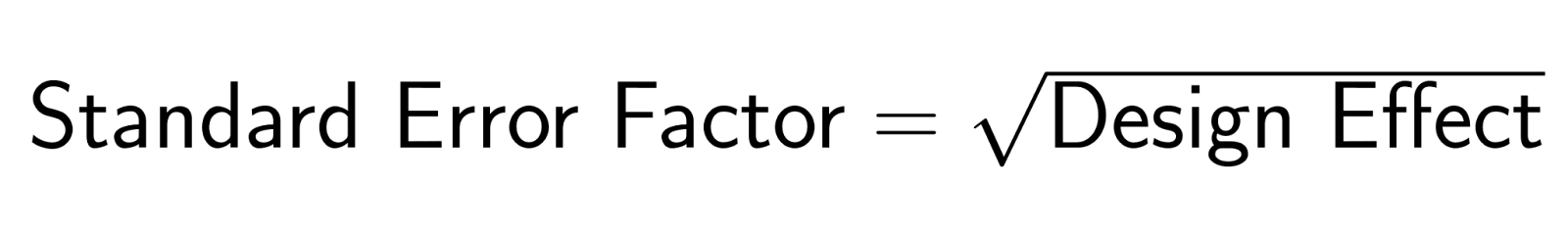
Cuando los miembros de la familia tienen opiniones similares (ρ = 0,3) y el tamaño medio del hogar es de 3, el efecto del diseño es DE = 1 + (3-1)(0,3) = 1,6. El factor de error estándar es √1,6 = 1,27, lo que hace que los errores estándar sean un 27 % mayores que los que se obtendrían con un muestreo aleatorio simple.

Aplicaciones en inferencia estadística

El error estándar sustenta algunas de las técnicas más importantes en la inferencia estadística, desde los intervalos de confianza hasta las pruebas de hipótesis. En esta sección se analiza cómo el error estándar hace que estos procedimientos fundamentales sean posibles y fiables.

Construcción del intervalo de confianza

El error estándar determina directamente el intervalo de confianza :

Para muestras grandes, el valor crítico es aproximadamente 1,96 para un nivel de confianza del 95 %. Las muestras más pequeñas utilizan valores críticos de distribución t ligeramente superiores. Esta relación explica por qué los investigadores suelen informar de los errores estándar junto con las estimaciones puntuales. Proporcionan información inmediata sobre la precisión de los resultados.

Los intervalos estrechos indican estimaciones precisas con pequeños errores estándar, mientras que los intervalos amplios sugieren una incertidumbre considerable. El nivel de confianza (95 %, 99 %, etc.) determina el grado de confianza que deseamos tener, pero la amplitud del intervalo depende fundamentalmente del error estándar.

Marco de prueba de hipótesis

El error estándar estandariza las estadísticas de prueba convirtiendo las diferencias brutas en unidades de variabilidad muestral:

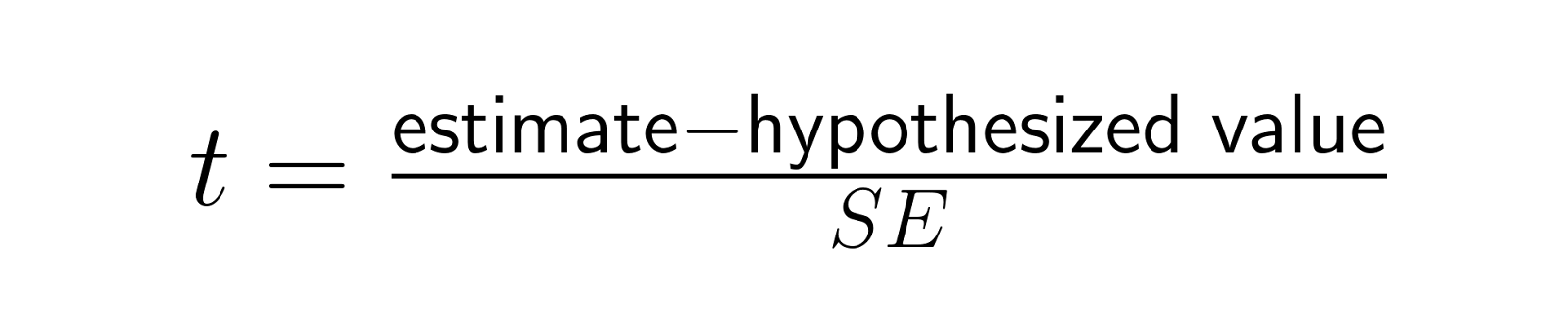
Esta estadística t permite realizar comparaciones significativas entre diferentes estudios y tamaños del efecto, al expresar las diferencias en relación con su variabilidad esperada bajo la hipótesis nula. Una diferencia de 5 puntos puede ser significativa con SE = 1 (lo que da t = 5), pero insignificante con SE = 10 (lo que da t = 0,5), lo que ilustra cómo el error estándar proporciona el contexto para interpretar los tamaños del efecto.

Dado que las pruebas estadísticas dividen el efecto observado por el error estándar, los errores estándar más pequeños hacen que incluso los efectos reales modestos alcancen significación estadística, mientras que los errores estándar más grandes requieren efectos más grandes para alcanzar significación. Esto explica por qué los estudios a gran escala pueden detectar efectos pequeños pero reales que los estudios más pequeños pasarían por alto.

Aplicaciones metaanalíticas

En el metaanálisis, el error estándar determina la ponderación que se asigna a cada estudio mediante la ponderación por varianza inversa:

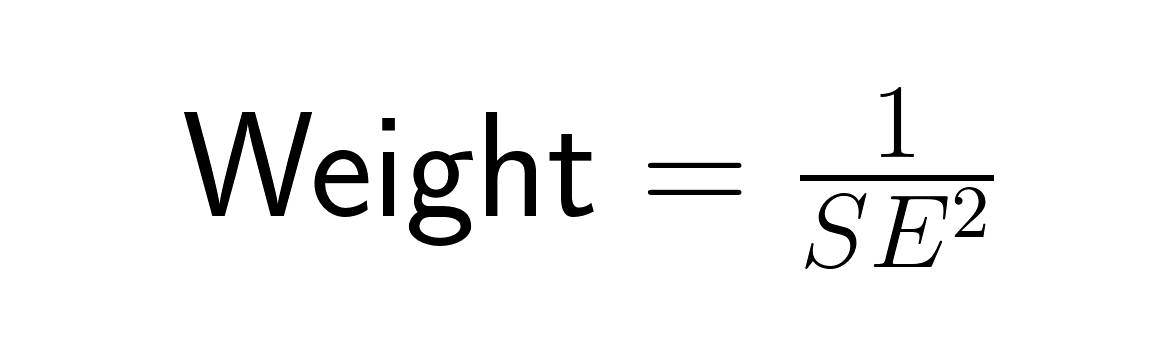
Los estudios con errores estándar más pequeños (estimaciones más precisas) reciben mayor peso que los estudios con errores estándar más grandes, lo que refleja el principio de que las estimaciones más precisas deben contribuir más a nuestra comprensión general. Un estudio con un error estándar de 0,5 recibe cuatro veces más peso que un estudio con un error estándar de 1,0, lo que combina de forma óptima la información de todos los estudios para minimizar el error estándar global de la estimación metaanalítica.

Informes e interpretación del error estándar

Una comunicación clara sobre el error estándar requiere prestar atención tanto al formato de presentación como al contexto interpretativo. A continuación se destacan algunas orientaciones prácticas para presentar los resultados del error estándar y evitar errores de interpretación comunes. 

Mejores prácticas para la presentación de informes

Especifica siempre qué tipo de error estándar estás notificando y utiliza un formato coherente. Utiliza formatos como «Media (SE)», por ejemplo «45,2 (2,8)» en las tablas. Para los gráficos, utiliza barras de error que se extiendan un error estándar por encima y por debajo de las estimaciones puntuales, pero indica claramente si las barras de error representan el error estándar, la desviación estándar o los intervalos de confianza.

Interpretación en regresión y modelos

La salida de la regresión muestra los errores estándar junto con las estimaciones de los coeficientes. Un coeficiente de 0,75 con SE = 0,25 sugiere que el efecto real probablemente se sitúe entre 0,25 y 1,25 aproximadamente, mientras que la estadística t de 3,0 indica una fuerte evidencia en contra de la hipótesis nula.

Consideraciones sobre el error no muestral

El error estándar cuantifica únicamente la variabilidad del muestreo. No incluye errores de medición, sesgos por falta de respuesta u otras fuentes de incertidumbre. Los sesgos sistemáticos, como el sesgo de selección o la confusión, pueden generar estimaciones inexactas, independientemente de lo pequeño que sea el error estándar. No dejes que los pequeños errores estándar generen un exceso de confianza en resultados que aún podrían estar sistemáticamente sesgados.

Interpretaciones erróneas y errores comunes

Una interpretación cuidadosa del error estándar requiere ser consciente de los conceptos erróneos frecuentes que pueden llevar a conclusiones incorrectas. Esta sección aborda las fuentes más comunes de confusión y ofrece orientación para evitar errores de interpretación.

Error estándar frente a desviación estándar

El error estándar y la desviación estándar miden diferentes aspectos de la variabilidad y no deben confundirse, aunque esta confusión aparece con frecuencia tanto en informes de investigación como en la cobertura de los medios de comunicación populares. La desviación estándar describe la dispersión de las observaciones individuales alrededor de la media muestral, respondiendo a la pregunta «¿En qué medida varían los puntos de datos individuales con respecto a la media?». El error estándar describe la precisión de la media muestral como estimación de la media poblacional, respondiendo a la pregunta «¿En qué medida variarían las medias muestrales si repitiéramos el estudio?».

La relación matemática ayuda a aclarar la distinción:

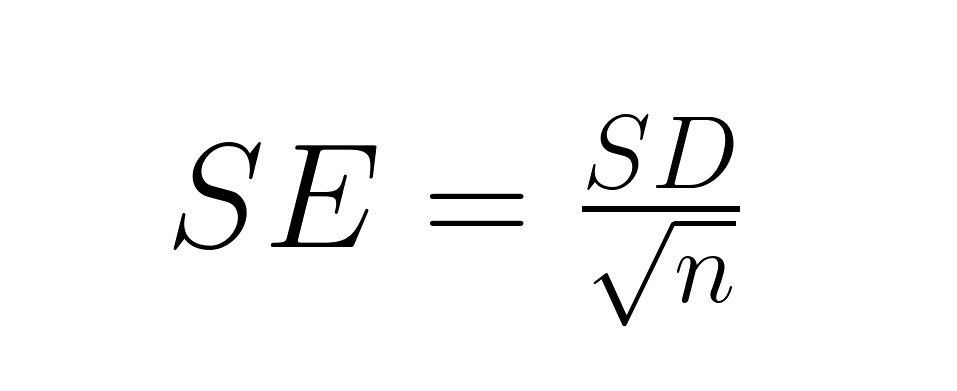
El error estándar es igual a la desviación estándar dividida por la raíz cuadrada del tamaño de la muestra, por lo que el error estándar siempre es menor que la desviación estándar (excepto cuando n = 1). Un conjunto de datos sobre la estatura de adultos podría tener una desviación estándar de 4 pulgadas (lo que indica que la estatura de cada individuo varía considerablemente), pero un error estándar de 0,1 pulgadas para la media muestral (lo que indica una estimación muy precisa de la estatura media). 

Conceptos erróneos sobre precisión y exactitud

El error estándar mide la precisión, no la exactitud. Un error estándar pequeño indica una alta precisión, ya que muestras repetidas producirían estimaciones similares, pero la exactitud puede verse comprometida por sesgos sistemáticos.

Piensa en una báscula de baño que siempre marca 5 libras de más: pesarte 100 veces produciría mediciones muy precisas (pequeño error estándar), pero resultados constantemente inexactos. Un error estándar bajo no garantiza resultados correctos.

Desventajas y limitaciones

Los cálculos del error estándar asumen un muestreo aleatorio, observaciones independientes y, a menudo, normalidad. El muestreo no aleatorio hace que el error estándar sea inadecuado, mientras que las observaciones correlacionadas (como los estudiantes dentro de las escuelas) requieren errores estándar más grandes.

No consideres el bajo error estándar como una «prueba» del resultado. Un ensayo controlado aleatorio con un error estándar pequeño proporciona pruebas más sólidas que un estudio observacional con un error estándar igualmente pequeño, ya que el diseño del estudio afecta a la validez independientemente de la precisión estadística. Nuestro Diseño experimental en R cubre los principios de aleatorización adecuada, bloqueo y control experimental que garantizan que los cálculos de error estándar conduzcan a conclusiones válidas.

Extensiones metodológicas avanzadas

La práctica estadística moderna ha desarrollado alternativas y ampliaciones a los enfoques clásicos del error estándar, ofreciendo soluciones cuando los métodos tradicionales se quedan cortos o cuando se necesita una cuantificación más sofisticada de la incertidumbre.

Las técnicas de bootstrapping ofrecen un enfoque no paramétrico que no se basa en supuestos distributivos. Mediante el remuestreo repetido de los datos originales, los métodos bootstrap estiman los errores estándar para estadísticas complejas en las que no existen fórmulas analíticas. Nuestro muestreo en Python cubre las técnicas de bootstrap.

Los errores estándar robustos ajustan las violaciones de los supuestos. Los errores estándar consistentes con la heteroscedasticidad siguen siendo válidos cuando la varianza residual no es constante, mientras que los errores estándar agrupados tienen en cuenta la correlación dentro de los grupos. Estos métodos suelen producir errores estándar más grandes, lo que proporciona una inferencia más conservadora.

Los enfoques bayesianos cuantifican la incertidumbre mediante distribuciones a posteriori en lugar de errores estándar. Los intervalos de credibilidad bayesianos proporcionan afirmaciones de probabilidad directas: «Hay un 95 % de probabilidad de que el parámetro se encuentre entre 2,1 y 4,7». Explora nuestro Modelo de regresión bayesiano con rstanarm para aprender cómo los métodos bayesianos manejan la incertidumbre de manera diferente.

Conclusión

El error estándar une los datos muestrales y las inferencias poblacionales, cuantificando la precisión de nuestras estimaciones y permitiendo obtener conclusiones estadísticas significativas. La idea clave: el error estándar mide la precisión, no la exactitud. Nos indica cuán consistentes serían nuestras estimaciones en muestras repetidas, no si esas estimaciones son correctas.

Utiliza el error estándar de forma adecuada verificando las hipótesis, eligiendo el tipo correcto e interpretando los resultados en el contexto más amplio del diseño del estudio. Informa siempre de los errores estándar junto con las estimaciones puntuales, especifica qué tipo estás utilizando y reconoce las limitaciones. Considera la posibilidad de explorar métodos avanzados a través de nuestra Inferencia estadística en R para obtener una comprensión más profunda a través de un programa

Ya sea que estés diseñando experimentos, analizando datos de encuestas o interpretando resultados de investigaciones, el error estándar proporciona la base para una cuantificación honesta de la incertidumbre que genera confianza en los hallazgos estadísticos.