Loi des grands nombres : Une clé pour comprendre l'incertitude

Un seul résultat n'est pas très révélateur. Supposons que vous jouiez une fois à pile ou face et que vous obteniez pile. Cela ne prouve rien : il a pu atterrir de cette façon par hasard. Mais si vous jouez à pile ou face 100 fois, vous verrez que le nombre de piles et de faces est à peu près égal. C'est alors que la moyenne prend tout son sens.

C'est ce que prévoit la loi des grands nombres. Plus vous collectez de données, plus votre moyenne devient précise. Il vous aide à avoir une vue d'ensemble.

Dans ce guide, nous verrons ce que signifie la loi des grands nombres, comment elle fonctionne dans la vie réelle et pourquoi elle est si utile lorsque vous essayez de comprendre des modèles ou de prendre de meilleures décisions au fil du temps.

Qu'est-ce que la loi des grands nombres ?

Laloi des grands nombres est un principe de probabilité et de statistique qui explique comment les averages se comportent au fur et à mesure que l'on recueille des données. Au fur et à mesure que la taille de votre échantillon augmente, la moyennede cet échantillon (appelée moyenne de l'échantillon) se rapproche de la véritable moyenne de l'ensemble du groupe (appelée moyenne de la population).

Dans le monde réel, nous n'avons généralement pas accès aux données d'une population entière. Au lieu de cela, nous prenons un échantillon comme une enquête auprès de 1 000 électeurs, au lieu de l'ensemble des 300 millions de personnes. La loi des grands nombres nous permet de croire qu'avec suffisamment de données, la moyenne de l'échantillon sera proche de la réalité.

Au fur et à mesure que l'échantillon s'agrandit, les variations aléatoires commencent à s'annuler. Les valeurs aberrantes ont moins d'impact et la moyenne devient plus stable et prévisible.

Il existe deux versions principales de la loi, qui diffèrent par le degré de garantie de cet effet :

Loi faible (convergence en probabilité)

La loi faible des grands nombres indique que la moyenne de l'échantillon se rapprocheprobablement de la moyenne de la population à mesure que la taille de l'échantillon augmente. Plus vous recueillez de données, moins il est probable que votre moyenne reste éloignée de la réalité.

Par exemple, vous jouez à pile ou face. Au fur et à mesure que vous effectuez des lancers, le rapport entre le pile et le face se rapproche de 50/50. L'atterrissage n'est peut-être pas parfait, mais il s'en rapproche, et c'est là l'objectif de la loi faible.

Loi forte (convergence presque sûre)

La loi des grands nombres va encore plus loin. Cela signifie que la moyenne de l'échantillon se rapprochera de la moyenne de la population et y restera presque certainement, et pas seulement probablement.

En termes simples : si vous continuez à jouer à pile ou face à l'infini, le ratio pile/face ne s'approchera pas de 50/50 ; il s'y stabilisera. Cette loi nous donne donc la certitude quasi-totale que les moyennes à long terme reflètent la vérité, à de rares exceptions près.

Exemples concrets d'application de la loi

Prenons quelques exemples concrets pour comprendre le fonctionnement de cette loi :

Lancer de pièces ou de dés

Imaginez que vous lanciez trois fois un dé ordinaire à six faces. Vous pouvez obtenir des résultats tels que 6, 2 et 5. La moyenne est de 4,3, ce qui est supérieur à la valeur attendue de 3,5. Mais maintenant, vous lancez le dé 100 fois, puis 1 000 fois. Au fur et à mesure que le nombre de jets augmente, votre moyenne se rapproche de 3,5. La loi des grands nombres atténue le caractère aléatoire au fil du temps.

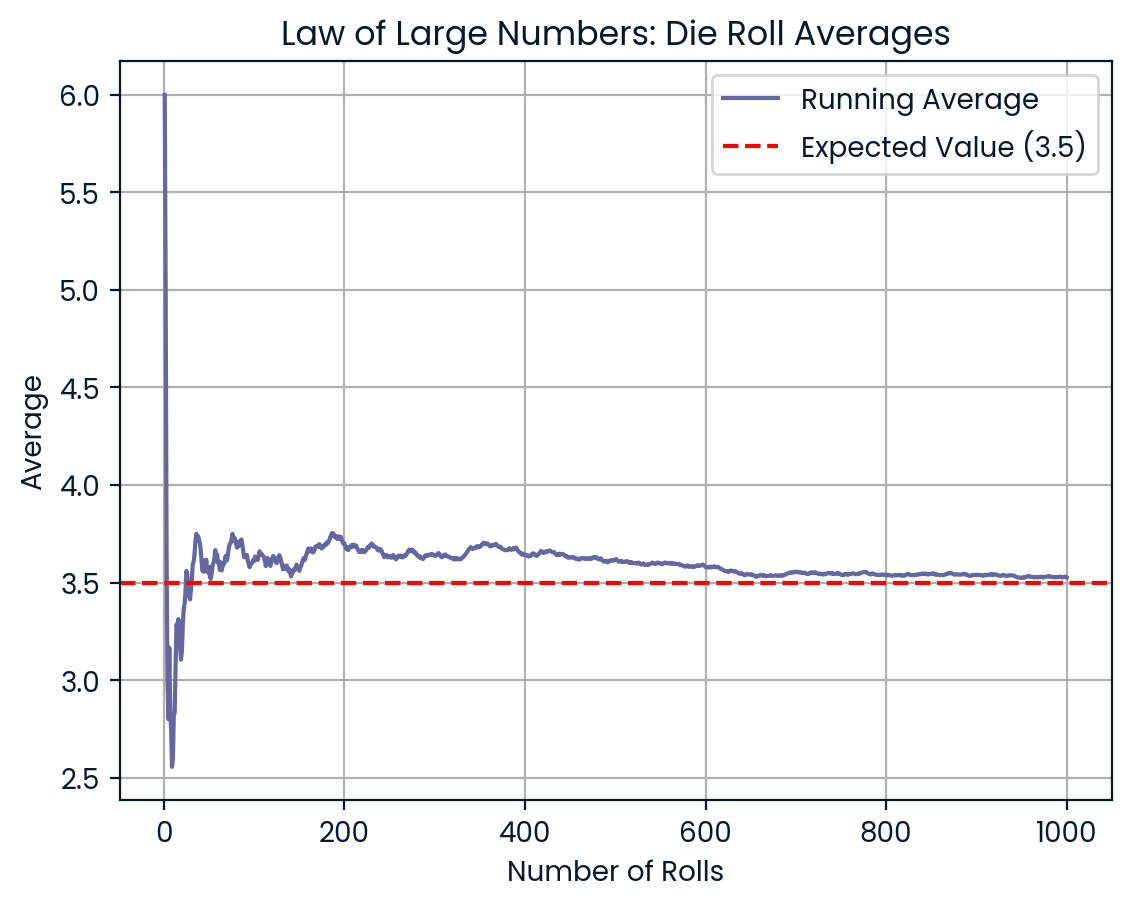
Plus il y a de rouleaux, plus la moyenne se rapproche de 3,5. Image par l'auteur.

Statistiques sportives

Les athlètes peuvent avoir de bons et de mauvais jours. Un quarterback peut réussir 9 passes sur 10 au cours d'un match, soit un taux impressionnant de 90 %. Mais cela ne signifie pas qu'ils jouent toujours à ce niveau.

Sur une saison entière, avec des centaines de lancers, le pourcentage de réussite commence à se stabiliser. Cette statistique sur l'ensemble de la saison donne une bien meilleure idée de la capacité réelle du joueur.

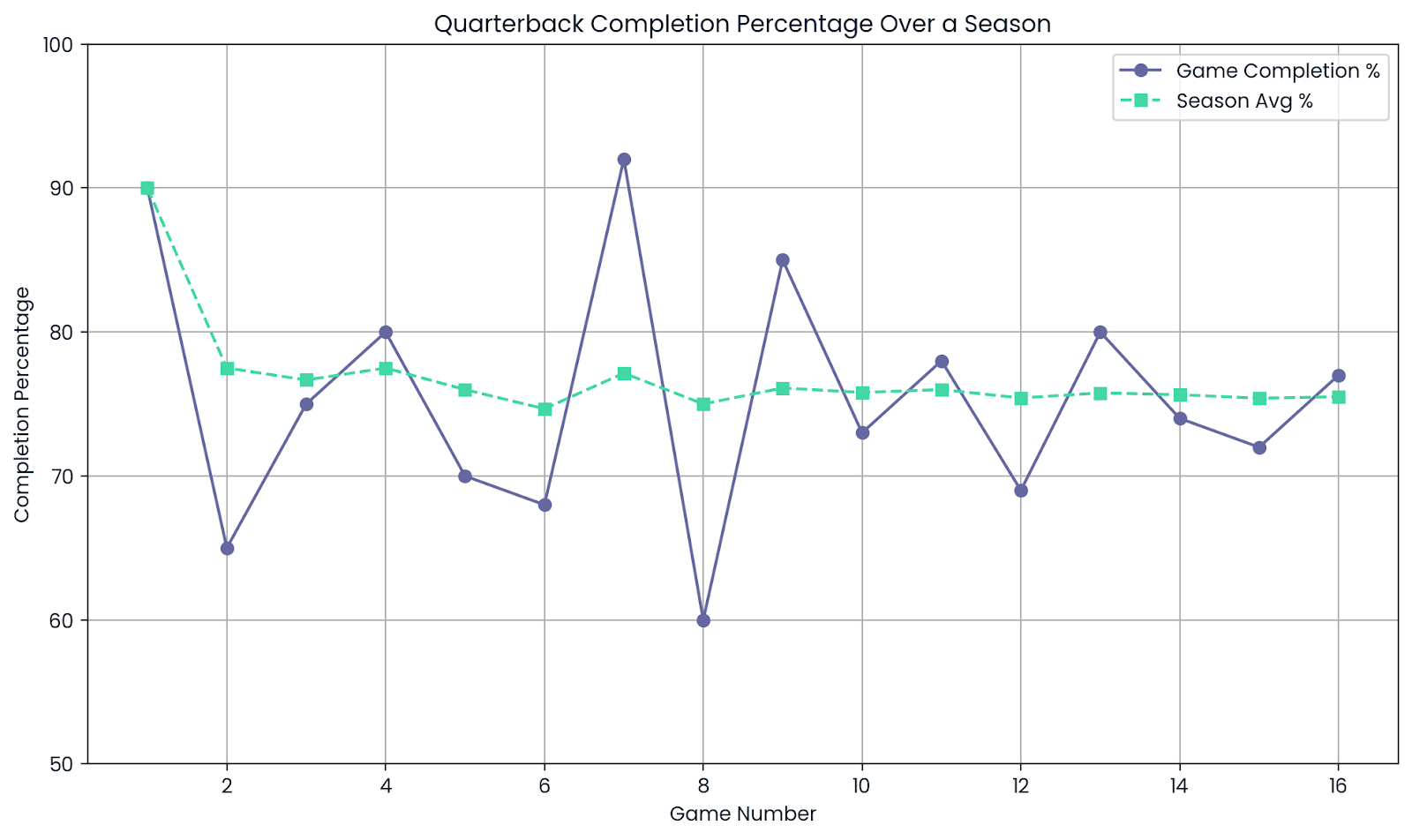
Moyenne. Image par l'auteur.

Mutualisation des risques dans le secteur de l'assurance 

Les compagnies d'assurance ne savent pas exactement combien une personne leur coûtera. Certaines personnes n'ont recours à aucun soin médical, tandis que d'autres le font.

Mais lorsque vous observez un grand groupe de personnes, ces hauts et ces bas s'équilibrent. En regroupant les risques de milliers d'assurés, les assureurs peuvent prévoir le coût moyen avec plus de précision.

Cela leur permet de fixer des prix (primes) équitables tout en restant financièrement stables.

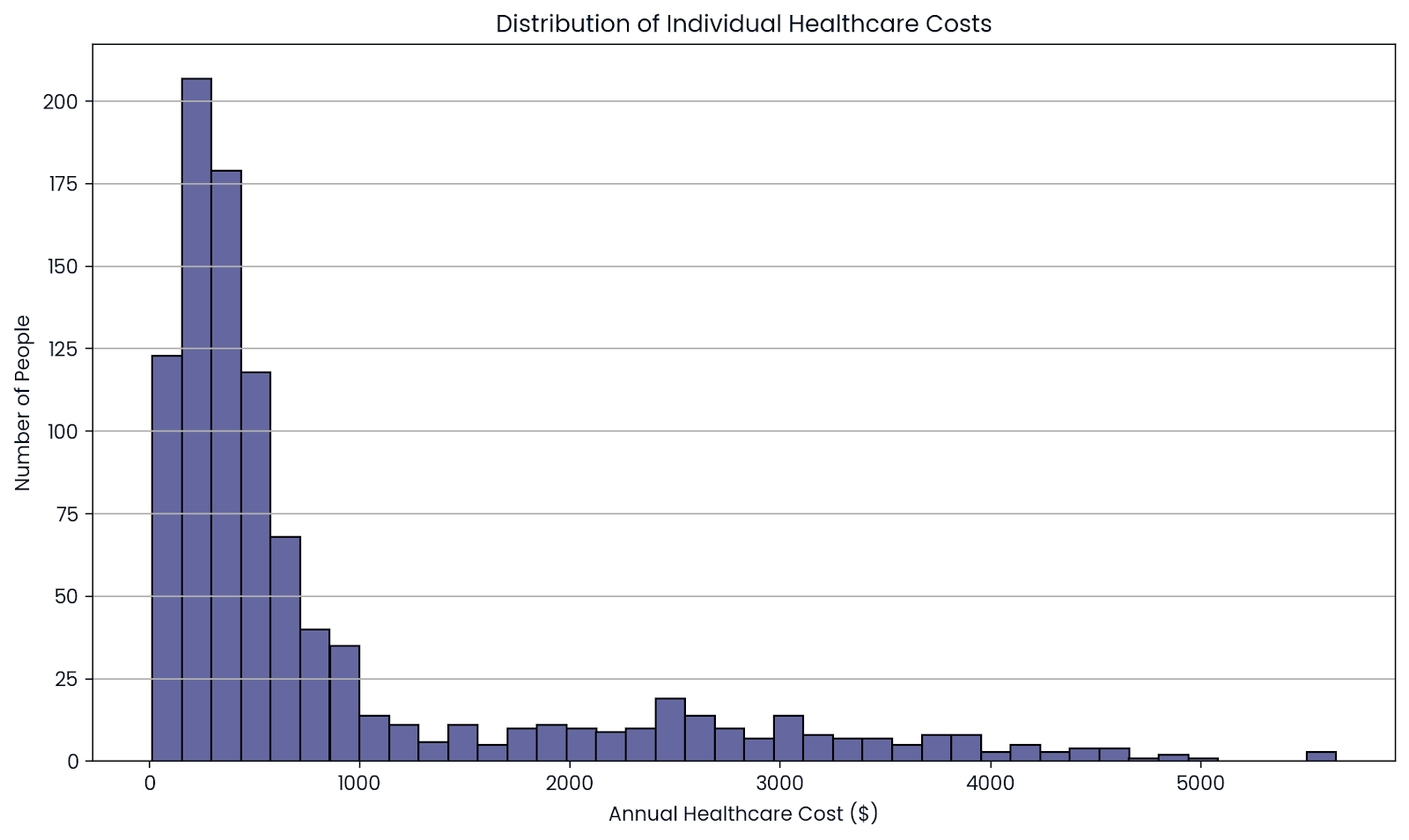
La moyenne sur un grand nombre de personnes montre le coût réel. Image par l'auteur.

Jeux de casino et avantage de la maison

Les casinos ont un léger avantage dans tous les jeux. Si vous jouez au blackjack, vous pouvez gagner cinq mains d'affilée ou en perdre dix. Mais sur des milliers de jeux, le résultat moyen est en faveur du casino.

Par exemple, si l'avantage de la maison est de 0,5 %, le casino s'attend à gagner en moyenne 50 cents par tranche de 100 dollars misés. Ce n'est peut-être pas le cas lors d'une courte session, mais sur des millions de jeux, le résultat est exactement celui escompté.

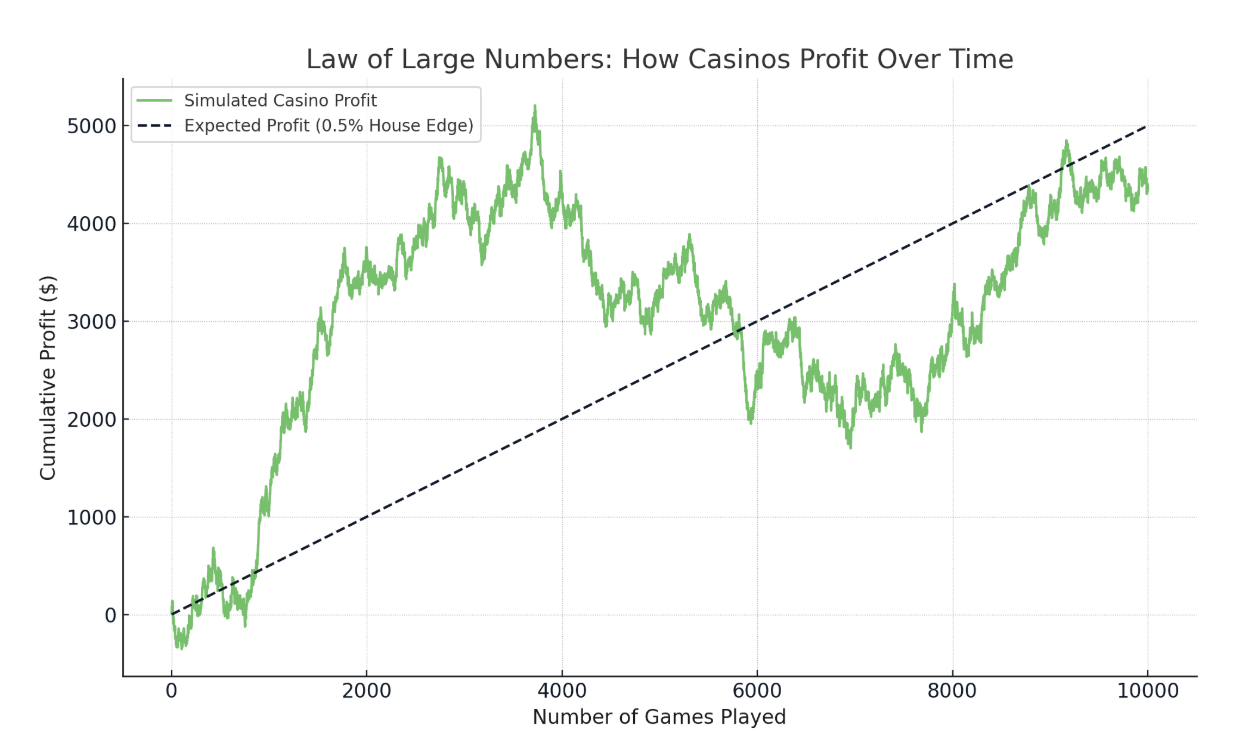
L'avantage du casino l'emporte lorsque les mises sont plus nombreuses. Image par l'auteur.

Les tests A/B dans les entreprises technologiques

Supposons qu'une entreprise souhaite tester deux versions d'un bouton de site web : Bouton A et Bouton B. Après que 20 personnes ont essayé chacun des boutons, le Bouton A semble meilleur. Mais ce ne sont pas des données suffisantes pour se fier au résultat.

Maintenant, laissez 20 000 utilisateurs voir les deux. Au fur et à mesure que la taille de l'échantillon augmente, les taux de clics moyens deviennent plus fiables et le bouton le plus performant devient évident.

C'est pourquoi les entreprises s'appuient sur de larges échantillons pour les tests A/B. La loi des grands nombres les aide à éviter les faux positifs et à faire des choix plus judicieux.

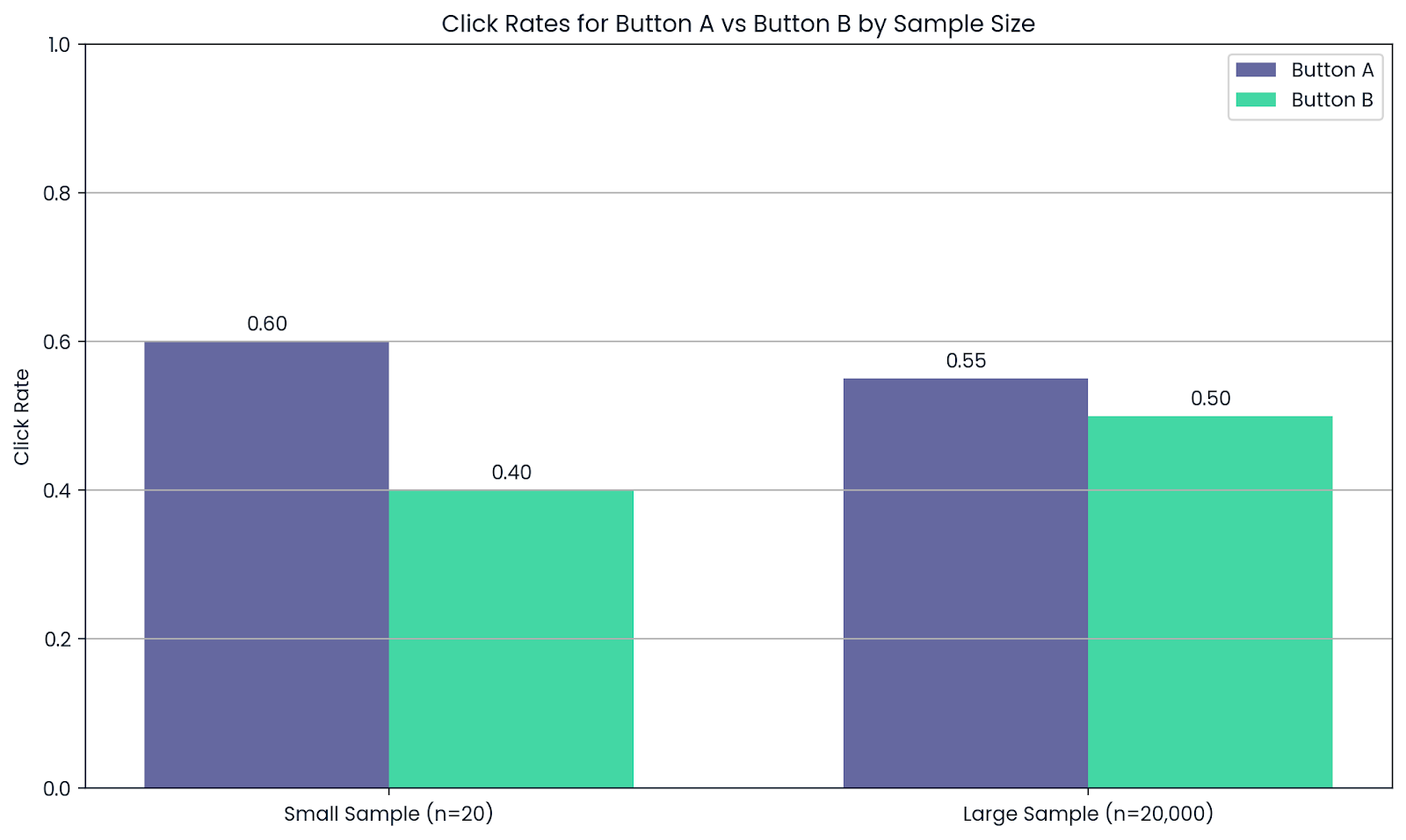
Un plus grand nombre de personnes testées signifie des résultats plus fiables. Image par l'auteur.

L'importance de la loi des grands nombres

En science des données, nous utilisons souvent des données pour former des modèles. Mais si l'ensemble de données est trop petit, quelques valeurs inhabituelles peuvent fausser les résultats.

Par exemple, vous testez un nouvel algorithme de recommandation en utilisant seulement 10 utilisateurs. Si un utilisateur clique sur tout et qu'un autre ne clique sur rien, votre performance moyenne peut sembler bonne ou mauvaise. Cela ne signifie pas que le modèle est bon ou mauvais, mais que votre échantillon est trop petit pour être fiable.

La loi des grands nombres nous dit que plus nous recueillons de données, plus les fluctuations aléatoires s'atténuent et plus le résultat moyen devient fiable. C'est pourquoi les grands ensembles de données permettent de faire de meilleures prédictions et de mieux comprendre les choses.

On le constate également dans les simulations. Prenons l'exemple des méthodes de Monte Carlo. Il s'agit d'exécuter le même scénario des milliers de fois en utilisant des entrées aléatoires. La loi des grands nombres garantit que plus nous effectuons d'essais, plus le résultat moyen se rapproche du véritable résultat attendu.

Dans l'apprentissage automatique, la loi se manifeste de deux manières importantes :

• Modèle de formation : Un modèle formé sur un petit ensemble de données déséquilibré peut apprendre des modèles qui ne reflètent pas le monde réel. Mais avec suffisamment de données diverses, le modèle apprend ce qui fonctionne réellement.
• Modèle de test : Tester un modèle sur seulement 50 utilisateurs peut donner des résultats très différents de ceux obtenus sur 5 000 utilisateurs. Un ensemble de tests plus large donne une image plus claire de la façon dont le modèle fonctionnera une fois déployé.

En bref, plus de données signifie moins de bruit et de meilleures décisions. 

Idées reçues

La loi des grands nombres est souvent mal comprise lorsque les gens s'attendent à ce qu'elle fonctionne instantanément.

Si vous pensez que les résultats s'équilibreront rapidement, c'est une erreur. Par exemple, si vous jouez à pile ou face et que vous obtenez cinq fois de suite le résultat "face", vous pouvez penser que le résultat "pile" est maintenant "dû" pour équilibrer les choses. Mais ce n'est pas ainsi que fonctionnent les probabilités.

Ce raisonnement est connu sous le nom de sophisme du joueur : l'idée fausse que les résultats passés influencent les résultats futurs dans le cadre d'un processus véritablement aléatoire. En réalité, chaque pile ou face est toujours une chance sur deux, peu importe ce qui s'est passé avant.

La loi des grands nombres ne promet pas que le hasard s'atténuera à court terme. Au contraire, il nous indique qu'après de très nombreux essais, le résultat moyen se rapproche de la valeur attendue. Dans le cas d'une pièce de monnaie équitable, cela signifie qu'une moitié de pile et une moitié de face finiront par apparaître, et non immédiatement.

De courtes périodes ou des schémas inhabituels peuvent toujours se produire en cours de route. C'est ainsi que le hasard apparaît dans de petits échantillons. La loi ne prend tout son sens que lorsque vous faites un zoom arrière et que vous avez une vue d'ensemble.

Liens avec d'autres concepts

Si la loi des grands nombres nous dit que la moyenne de l'échantillon se rapproche de la vraie moyenne à mesure que la taille de l'échantillon augmente, le théorème de la limite centrale (CLT) va plus loin. Il explique à quoi ressemble la distribution de ces moyennes.

Selon le CLT, si vous prenez de nombreux échantillons de grande taille et que vous calculez leurs moyennes, ces moyennes formeront une courbe en forme de cloche (une distribution normale), quelle que soit la forme des données initiales. 

Les deux sont importants dans les statistiques, mais ils décrivent des choses différentes : l'un se concentre sur la précision, l'autre sur la forme.

Principaux enseignements

La loi des grands nombres met en évidence un principe fondamental de l'analyse des données : des échantillons plus importants donnent des résultats plus stables et plus précis, mais uniquement lorsque les données sont représentatives. 

Bien que les grands ensembles de données réduisent les effets de la variation aléatoire, il n'est pas toujours préférable d'avoir plus de données. Si les données sont biaisées ou déséquilibrées, même un ensemble massif de données peut produire des résultats trompeurs. Pour tirer des conclusions valables, il faut à la fois du volume et de la qualité.

Si vous souhaitez acquérir des bases plus solides dans ces concepts, le cours de réflexion statistique en Python est un excellent point de départ. À partir de là, explorez la distribution gaussienne pour comprendre comment la loi des grands nombres est liée à d'autres outils clés des statistiques et de l'apprentissage automatique.