ARIMA para previsão de séries temporais: Um guia completo

Vamos dar uma olhada no ARIMA, que é uma das técnicas de previsão de séries temporais mais populares (se não a mais popular). O ARIMA é popular porque modela com eficácia os dados de séries temporais, capturando os componentes autorregressivos (AR) e de média móvel (MA) e, ao mesmo tempo, abordando a não estacionariedade por meio da diferenciação (I). Essa combinação torna os modelos ARIMA especialmente flexíveis e é por isso que eles são usados em diversos setores, como o financeiro e o de previsão do tempo. 

Os modelos ARIMA são altamente técnicos, mas vou detalhar as partes para que você possa desenvolver um bom entendimento. Antes de começar, é uma boa ideia que você se familiarize com algumas ferramentas básicas. O DataCamp oferece muitos recursos bons, como nossos cursos Modelos ARIMA em Python ou Modelos ARIMA em R. Você pode escolher qualquer um deles, dependendo do idioma que preferir. 

Por que usar a previsão ARIMA? 

Em finanças, economia e ciências ambientais etc., o ARIMA tem grande interesse porque pode identificar muitos padrões complexos de nossas observações passadas com necessidades futuras, o que o torna uma técnica de última geração. Desde a previsão do preço das ações, passando pela previsão de padrões climáticos até a obtenção de uma ideia sobre a demanda do consumidor, o ARIMA é uma ótima maneira de fazer análises preditivas precisas e acionáveis.

Com o uso do ARIMA, podemos analisar e prever dados de séries temporais de forma sofisticada, levando em conta padrões, tendências e sazonalidade. Isso facilita uma visão de 360 graus da dinâmica subjacente para que você possa tomar decisões informadas.

Componentes principais dos modelos ARIMA

Para realmente entender o ARIMA, precisamos desconstruir seus blocos de construção. Quando tivermos os componentes definidos, será mais fácil entender como esse método de previsão de séries temporais funciona como um todo. Aqui, darei uma explicação detalhada de cada componente.

Parte autorregressiva (AR)

O componente autorregressivo (AR) cria uma tendência altamente necessária a partir de valores passados na estrutura AR para modelos preditivos. Para esclarecer, a "estrutura de autorregressão" funciona como um modelo de regressão em que você usa as defasagens dos valores passados da própria série temporal como regressores.

Usando uma ampla variedade de dados históricos, a estrutura interroga padrões importantes para poder expor a dinâmica sistêmica. Esses padrões históricos nos ajudam a entender quais tendências futuras poderão surgir e a definir alguns pontos prováveis da trajetória de valor que são essenciais para uma melhor tomada de decisão e uma previsão precisa. 

Parte integrada (I)

A parte Integrada (I) envolve a diferenciação do componente da série temporal, tendo em mente que nossa série temporal deve ser estacionária, o que realmente significa que a média e a variação devem permanecer constantes em um período de tempo. Basicamente, subtraímos uma observação de outra para que as tendências e a sazonalidade sejam eliminadas. Ao realizar a diferenciação, obtemos a estacionariedade. Essa etapa é necessária porque ajuda o modelo a se ajustar aos dados e não ao ruído.

Parte da média móvel (MA) 

O componente de média móvel (MA) concentra-se na relação entre uma observação e um erro residual (falhas nos valores observados-previstos) de observações defasadas. Observando como a observação atual está relacionada aos erros do passado, podemos inferir algumas informações úteis sobre qualquer possível tendência em nossos dados. 

Podemos considerar os resíduos entre um desses erros, e o conceito do modelo de média móvel estima ou considera seu impacto em nossa última observação. Isso é particularmente útil para rastrear e capturar alterações de curto prazo nos dados ou choques aleatórios. Na parte (MA) de uma série temporal, podemos obter informações valiosas sobre seu comportamento, o que, por sua vez, nos permite fazer previsões e prognósticos com maior precisão.

Como criar um modelo ARIMA em Python

Para criar um modelo ARIMA para previsão, como os preços do ouro, você pode seguir estas etapas. Vamos analisar isso juntos.

Coleta de dados 

A primeira etapa é preparar um conjunto de dados adequado e preparar nosso ambiente.

Localizar um conjunto de dados

Colete ou pesquise um conjunto de dados em plataformas de fontes de dados. Você quer um que tenha dados históricos ao longo do tempo. Aqui está um link para o conjunto de dados do Kaggle relacionado aos preços futuros do ouro. 

Instalar pacotes

Instalamos os pacotes de que precisamos, incluindo statsmodels e sklearn. 

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error

Carregar os dados

Em seguida, lemos os dados em nosso ambiente local.

data = pd.read_csv("future-gc00-daily-prices.csv", index_col="Date")

Pré-processamento de dados 

Nosso conjunto de dados é bastante limpo, mas, em outros contextos, teríamos de lidar com problemas de indexação, o que é importante na previsão de séries temporais. Por exemplo, se estivéssemos prevendo o valor de abertura de uma ação em uma determinada bolsa, teríamos de considerar que o mercado de ações não abre nos fins de semana.

Verificar a estacionariedade

Manter as coisas estacionárias facilita muito a tarefa de modelagem, ajuda a melhorar a precisão do nosso modelo e, em troca, nos fornece previsões mais confiáveis. Embora os modelos ARIMA possam lidar com a não estacionariedade até certo ponto, eles não podem considerar efetivamente a variação no tempo. Aqui podemos usar o teste Augmented Dickey-Fuller para saber se nossos dados têm uma média e uma variância constantes.

result = adfuller(data["Price"])
print(f"ADF Statistic: {result[0]}")
print(f"p-value: {result[1]}")

Lidar com valores ausentes

Como parte do pré-processamento de dados, também precisamos considerar como lidar com os valores ausentes usando um método de imputação, como preenchimento direto ou substituição da média.

data.fillna(method='ffill', inplace=True)  # fill missing values

Realizar diferenciação

Para analisar a estacionariedade de nossos dados de série temporal, devemos primeiro calcular as diferenças em nossos dados. Se os dados não forem estacionários, aplique a técnica de diferenciação para transformá-los em uma série estacionária. As etapas a serem seguidas para realizar a diferenciação são as seguintes:

• Subtraia cada observação da seguinte para obter uma nova série temporal de primeiras diferenças. Isso cria uma nova série temporal com um elemento a menos do que a original.
• Teste se a série diferenciada agora é estacionária. Caso contrário, podemos obter a segunda diferença diferenciando a série original novamente.
• Continue diferenciando a série até que ela se torne estacionária. A ordem de diferenciação exigida é o número mínimo de diferenças necessárias para obter uma série sem autocorrelação.

if result[1] > 0.05:  
data["Price"] = data["Price"].diff().dropna()
result = adfuller(data["Price"])
stationarity_interpretation = "Stationary" if result[1] < 0.05 else "Non-Stationary"

print(f"ADF Statistic after differencing: {result[0]}")
print(f"p-value after differencing: {result[1]}")
print(f"Interpretation: The series is {stationarity_interpretation}.")

ADF Statistic: -11.498371141896145
p-value: 4.5550962204394835e-21
Interpretation: The series is Stationary.

Identificação do modelo

Quando criamos um modelo ARIMA, temos que considerar a p, de q que entram em nosso modelo ARIMA.

• O primeiro parâmetro, p, é o número de observações defasadas. Ao considerar p, determinamos efetivamente o quanto retrocedemos no tempo ao tentar prever a observação atual. Fazemos isso observando as autocorrelações de nossas séries temporais, que são as correlações em nossas séries em defasagens anteriores. 
• O segundo parâmetro, d, refere-se à ordem de diferenciação. Diferenciar significa simplesmente encontrar as diferenças entre os intervalos de tempo consecutivos. É uma maneira de tornar nossos dados estacionários, o que significa remover as tendências ou a sazonalidade. d indica a diferenciação em que ordem você obtém um processo estacionário.
• O terceiro parâmetro q refere-se à ordem da parte da média móvel (MA) do modelo. Representa o número de erros de previsão defasados incluídos no modelo. Diferentemente de uma média móvel simples, que suaviza os dados, a média móvel no ARIMA captura a relação entre uma observação e os erros residuais de um modelo de média móvel aplicado a observações defasadas.

Como encontrar os termos ARIMA

Usamos ferramentas como ACF (função de autocorrelação) e PACF (função de autocorrelação parcial) para determinar os valores de p, d e q. O número de defasagens em que a ACF corta é q, e em que a PACF corta é p. Também precisamos escolher o valor adequado para d, criando uma situação em que, após a diferenciação, os dados se assemelhem a ruído branco. Para nossos dados, escolhemos 1 para p e q porque observamos um pico significativo na primeira defasagem para cada um deles.

plot_acf(data["Price"], lags=40)
plot_pacf(data["Price"], lags=40)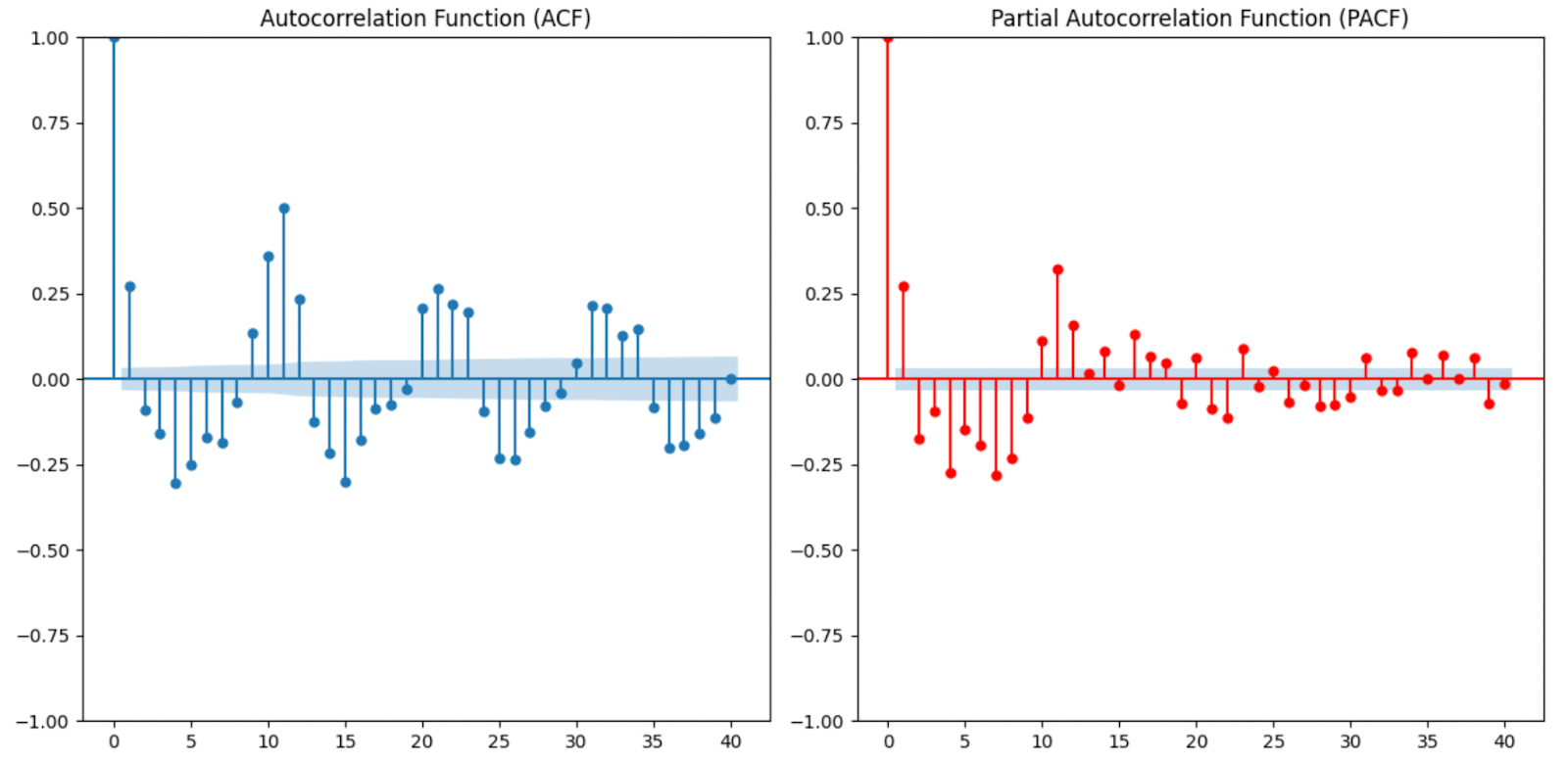

Gráficos ACF e PACF usados para determinar os termos ARIMA. Imagem do autor

Estimativa de parâmetros 

Para deixar claro, os valores p, d e q no ARIMA representam a ordem do modelo (defasagens para autorregressão, diferenciação e termos de média móvel), mas não são os parâmetros reais que estão sendo estimados. Depois que os valores de p, d e q são escolhidos, o modelo estima parâmetros adicionais, como coeficientes para os termos autorregressivos e de média móvel, por meio da estimativa de máxima verossimilhança (MLE).

Ajuste de modelo

# Fit the ARIMA model
# Initial ARIMA Model parameters
p, d, q = 1, 0, 1
model = ARIMA(data["Price"], order=(p, d, q))
model_fit = model.fit()
model_summary = model_fit.summary()
model_summary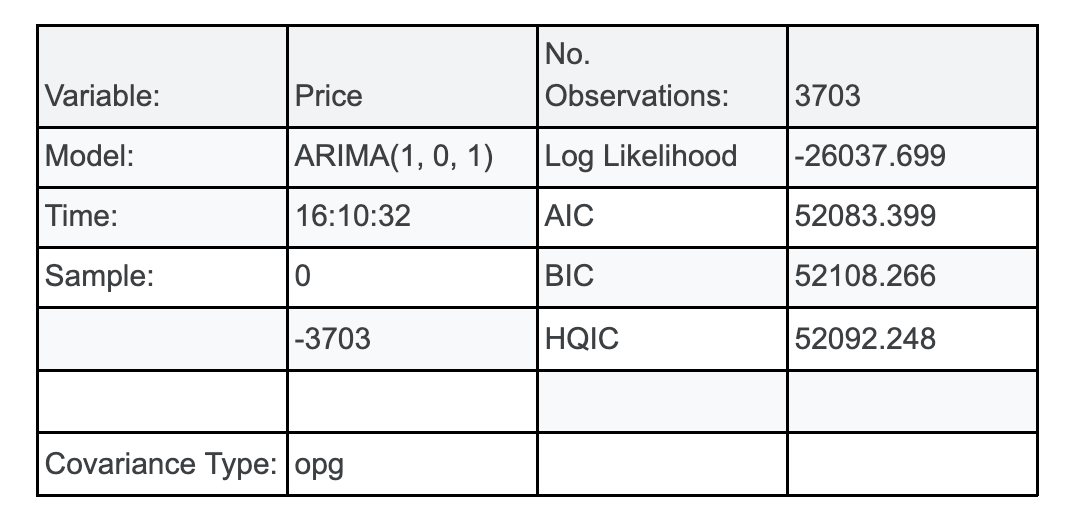

Estatísticas e diagnósticos de modelos

Agora, verificamos os resíduos e nos certificamos de que eles agem como ruído branco, o que significa que não devem ter padrões ou tendências. Uma opção é usar nossos gráficos ACF e PACF novamente, mas dessa vez aplicados aos resíduos. Se não houver grandes picos de defasagem nesses gráficos fora da banda, isso significa que nossos resíduos parecem ser ruído branco. Também podemos verificar os resíduos do modelo geral para garantir que não haja padrões óbvios, como estamos fazendo aqui:

Gráfico residual

# plot residual errors
residuals = model_fit.resid
residuals.plot()
residuals.plot(kind='kde')
plt.show()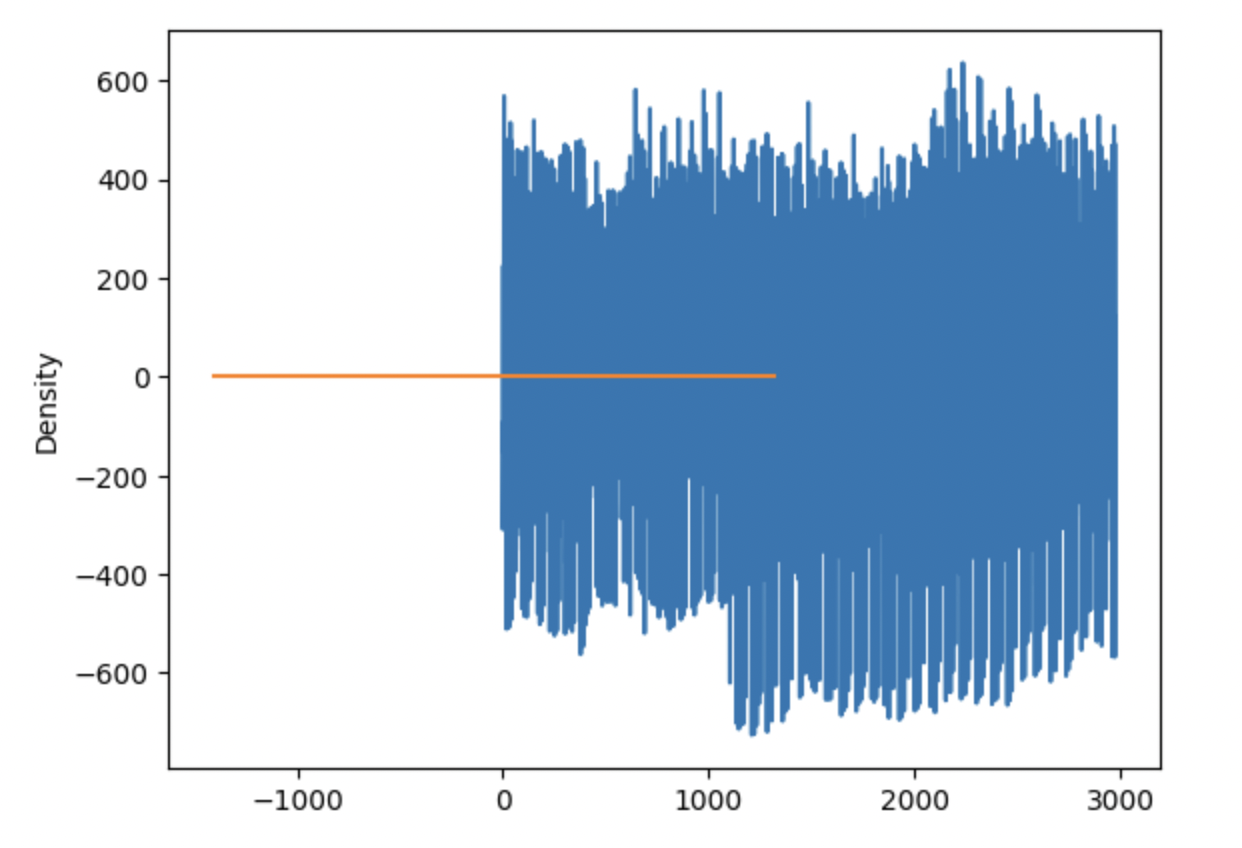

Resíduos do modelo ARIMA. Imagem do autor

AIC e BIC

Verificamos as estatísticas do modelo relevantes para a seleção do modelo. Valores mais baixos significam que o modelo se ajusta melhor, mas também podemos comparar os resultados com os resultados de modelos mais simples para evitar o ajuste excessivo.

print(f"AIC: {model_fit.aic}")
print(f"BIC: {model_fit.bic}")

AIC: 41919.18902176751
BIC: 41937.18705062565

Previsão

Para fazer previsões usando um modelo ARIMA, comece usando o modelo ajustado para prever valores futuros com base nos dados. Depois que as previsões são feitas, é útil visualizá-las plotando os valores previstos junto com os valores reais. Isso é feito porque usamos um fluxo de trabalho de treinamento/teste, em que os dados são divididos em conjuntos de treinamento e teste. Isso nos permite ver o desempenho do modelo em dados não vistos. Nosso curso Model Validation in Python é um ótimo recurso para que você aprenda os meandros da validação de modelos.

1. Use um fluxo de trabalho de treinamento/teste

Nossa primeira etapa é dividir os dados em versões de treinamento e teste. 

data = data[“Price”]train_size = int(len(data) * 0.8)train, test = data[:train_size], data[train_size:]

# Fit the model to training data. Replace p, d, q with our ARIMA parameters
model = ARIMA(train_data["Price"], order=(p, d, q))  

# Forecast
forecast = model_fit.forecast(steps=len(test))

2. Visualize nossa série temporal

Nossa próxima etapa é inspecionar visualmente nossa previsão de série temporal.

# Plotting
plt.figure(figsize=(10, 5))
plt.plot(data.index[:train_size], train, label='Train', color='blue')
plt.plot(data.index[train_size:], test, label='Test', color='green')
plt.plot(data.index[train_size:], forecast, label='Forecast', color='red')
plt.legend()
plt.title('ARIMA Forecast vs Actual')
plt.show()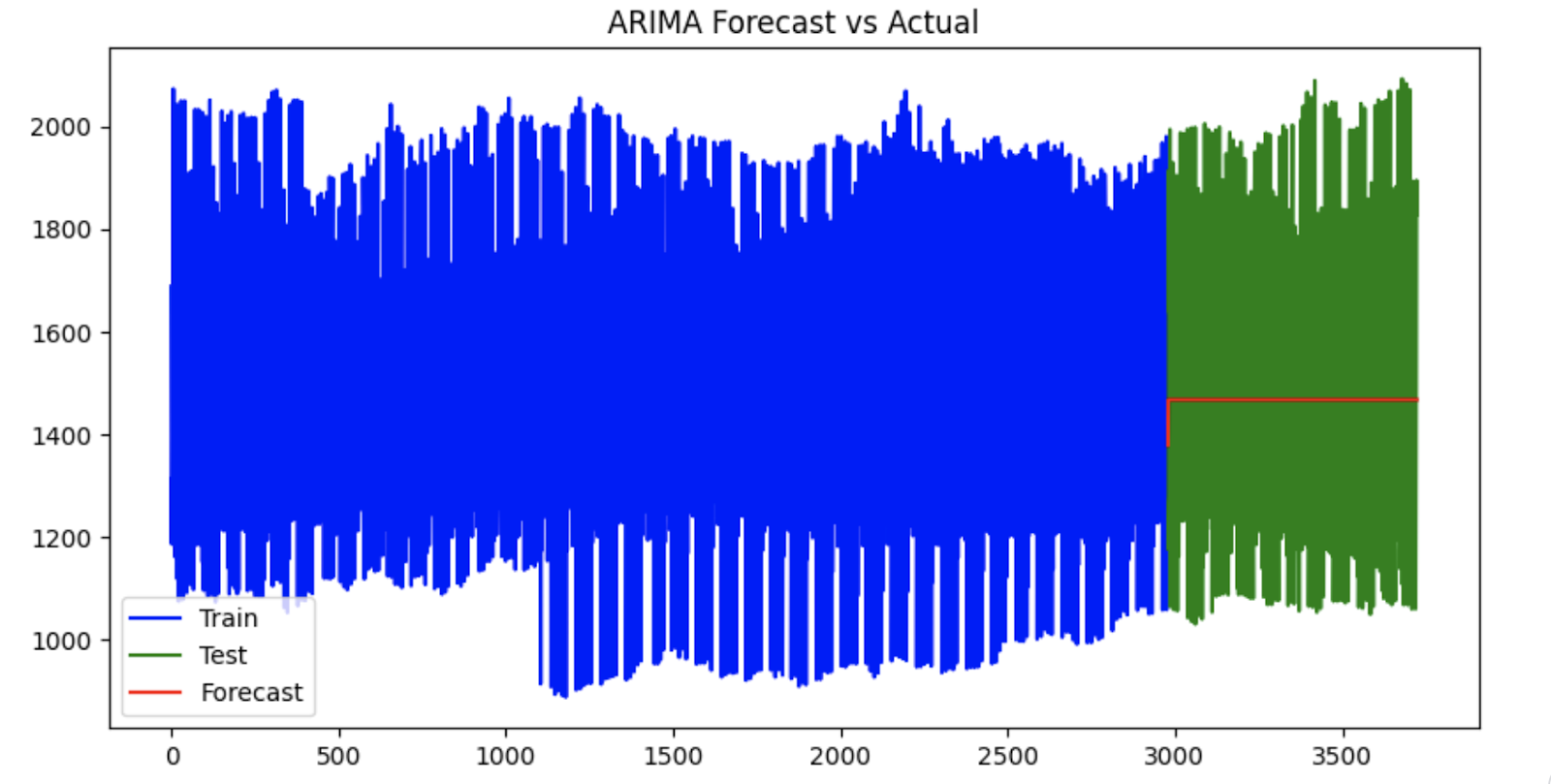

Previsão ARIMA de valores reais vs. valores previstos. Imagem do autor

3. Avaliar as estatísticas do modelo

Avaliamos as estatísticas do modelo, especialmente o erro quadrático médio, para avaliar o ajuste do nosso modelo. Um RMSE menor indica um modelo ARIMA melhor, refletindo diferenças menores entre os valores reais e os previstos.

# Evaluate model performance on the test set
rmse = mean_squared_error(test_data["Price"], predictions, squared=False)
print(f"RMSE: {rmse}")

“RMSE”: 135.87678712210163