ARIMA para la previsión de series temporales: Guía completa

Echemos un vistazo a ARIMA, que es una de las técnicas de previsión de series temporales más populares (si no la más popular). ARIMA es popular porque modela eficazmente los datos de las series temporales captando tanto los componentes autorregresivos (AR) como los de media móvil (MA), al tiempo que aborda la no estacionariedad mediante la diferenciación (I). Esta combinación hace que los modelos ARIMA sean especialmente flexibles, por lo que se utilizan en sectores muy diferentes, como las finanzas y la predicción meteorológica. 

Los modelos ARIMA son muy técnicos, pero voy a desglosarlos para que puedas desarrollar una sólida comprensión. Antes de empezar, conviene que te familiarices con algunas herramientas básicas. DataCamp ofrece un montón de buenos recursos, como nuestros cursos Modelos ARIMA en Python o Modelos ARIMA en R. Puedes elegir una u otra según la lengua que prefieras. 

¿Por qué utilizar la previsión ARIMA? 

En finanzas, economía y ciencias medioambientales, etc., ARIMA tiene un gran interés porque puede identificar muchos patrones complejos de nuestras observaciones pasadas con necesidades futuras, lo que la convierte en una técnica de vanguardia. Desde predecir el precio de las acciones, pronosticar patrones meteorológicos hasta hacerse una idea sobre la demanda de los consumidores, ARIMA es una forma estupenda de hacer análisis predictivos precisos y procesables.

Utilizando ARIMA, podemos analizar y predecir datos de series temporales de una forma sofisticada que tiene en cuenta patrones, tendencias y estacionalidad. Esto facilita una visión de 360 grados de la dinámica subyacente para tomar decisiones informadas.

Componentes clave de los modelos ARIMA

Para entender realmente el ARIMA, tenemos que deconstruir sus componentes básicos. Una vez que tengamos claros los componentes, será más fácil comprender cómo funciona este método de previsión de series temporales en su conjunto. Aquí daré una explicación detallada de cada componente.

Parte autorregresiva (AR)

El componente Autorregresivo (AR) construye una tendencia muy necesaria a partir de valores pasados en el marco AR para modelos predictivos. Para aclararlo, el "marco de autoregresión" funciona como un modelo de regresión en el que utilizas los retardos de los propios valores pasados de la serie temporal como regresores.

Utilizando una amplia variedad de datos históricos, el marco interroga patrones importantes para poder exponer la dinámica sistémica. Estas pautas históricas nos ayudan a comprender qué tendencias futuras podrían avecinarse y establecen algunos puntos probables de la trayectoria del valor que son imprescindibles para tomar mejores decisiones y hacer previsiones precisas. 

Parte integrada (I)

La parte Integrada (I) consiste en diferenciar el componente de la serie temporal teniendo en cuenta que nuestra serie temporal debe ser estacionaria, lo que en realidad significa que la media y la varianza deben permanecer constantes a lo largo de un periodo de tiempo. Básicamente, restamos una observación de otra para eliminar las tendencias y la estacionalidad. Realizando la diferenciación obtenemos la estacionariedad. Este paso es necesario porque ayuda a que el modelo se ajuste a los datos y no al ruido.

Parte de la media móvil (MA) 

El componente de media móvil (MA) se centra en la relación entre una observación y un error residual (fallos en los valores observados-predichos) de observaciones retardadas. Si observamos cómo se relaciona la observación actual con las de los errores pasados, podremos deducir alguna información útil sobre cualquier posible tendencia en nuestros datos. 

Podemos considerar los residuos entre uno de estos errores, y el concepto de modelo de media móvil estima o considera su impacto en nuestra última observación. Esto es especialmente útil para seguir y atrapar cambios a corto plazo en los datos o choques aleatorios. En la parte (MA) de una serie temporal, podemos obtener información valiosa sobre su comportamiento, lo que a su vez nos permite prever y predecir con mayor exactitud.

Cómo construir un modelo ARIMA en Python

Para construir un modelo ARIMA de previsión, como los precios del oro, puedes seguir estos pasos. Vamos a desglosarlo juntos.

Recogida de datos 

El primer paso es crear un conjunto de datos adecuado y preparar nuestro entorno.

Buscar un conjunto de datos

Recoge o busca un conjunto de datos de plataformas de fuentes de datos. Quieres uno que tenga datos históricos a lo largo del tiempo. Aquí tienes un enlace al conjunto de datos de Kaggle relacionados con los precios futuros del oro. 

Instalar paquetes

Instalamos los paquetes que necesitamos, incluidos statsmodels y sklearn. 

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error

Carga los datos

A continuación, leemos los datos en nuestro entorno local.

data = pd.read_csv("future-gc00-daily-prices.csv", index_col="Date")

Preprocesamiento de datos 

Nuestro conjunto de datos está bastante limpio, pero en otros contextos, tendríamos que problemas de indexación, lo que es importante en la previsión de series temporales. Por ejemplo, si tuviéramos que prever el valor de apertura de una acción en una bolsa determinada, tendríamos que tener en cuenta que la bolsa no abre los fines de semana.

Comprueba la estacionariedad

Mantener las cosas estacionarias facilita mucho la tarea de modelado, ayuda a mejorar la precisión de nuestro modelo y, a cambio, nos proporciona predicciones más fiables. Aunque los modelos ARIMA pueden tratar la no estacionariedad hasta cierto punto, no pueden dar cuenta eficazmente de la varianza variable en el tiempo. Aquí podemos utilizar la prueba Dickey-Fuller Aumentada para saber si nuestros datos tienen una media y una varianza constantes.

result = adfuller(data["Price"])
print(f"ADF Statistic: {result[0]}")
print(f"p-value: {result[1]}")

Tratar los valores perdidos

Como parte del preprocesamiento de datos, también tenemos que considerar cómo tratar los valores perdidos utilizando un método de imputación como el relleno hacia delante o el reemplazo de la media.

data.fillna(method='ffill', inplace=True)  # fill missing values

Realiza la diferenciación

Para analizar la estacionariedad de nuestros datos de series temporales, primero debemos calcular las diferencias de nuestros datos. Si los datos no son estacionarios, aplica la técnica de diferenciación para transformarlos en una serie estacionaria. Los pasos a seguir para realizar la diferenciación son:

• Resta cada observación de la siguiente para obtener una nueva serie temporal de primeras diferencias. Esto crea una nueva serie temporal que es un elemento más corta que la original.
• Comprueba si la serie diferenciada es ahora estacionaria. Si no es así, podemos tomar la segunda diferencia volviendo a diferenciar la serie original.
• Continúa diferenciando la serie hasta que sea estacionaria. El orden de diferenciación requerido es el número mínimo de diferencias necesario para obtener una serie sin autocorrelación.

if result[1] > 0.05:  
data["Price"] = data["Price"].diff().dropna()
result = adfuller(data["Price"])
stationarity_interpretation = "Stationary" if result[1] < 0.05 else "Non-Stationary"

print(f"ADF Statistic after differencing: {result[0]}")
print(f"p-value after differencing: {result[1]}")
print(f"Interpretation: The series is {stationarity_interpretation}.")

ADF Statistic: -11.498371141896145
p-value: 4.5550962204394835e-21
Interpretation: The series is Stationary.

Identificación del modelo

Cuando construimos un modelo ARIMA, tenemos que considerar la p, dy q que entran en nuestro modelo ARIMA.

• El primer parámetro, p, es el número de observaciones retardadas. Al considerar p, determinamos efectivamente cuánto nos remontamos en el tiempo al intentar predecir la observación actual. Para ello, nos fijamos en las autocorrelaciones de nuestras series temporales, que son las correlaciones de nuestras series en los retardos temporales anteriores. 
• El segundo parámetro, d, se refiere al orden de diferenciación. Diferenciar significa simplemente encontrar las diferencias entre pasos temporales consecutivos. Es una forma de hacer que nuestros datos sean estacionarios, lo que significa eliminar las tendencias o la estacionalidad. d indica la diferenciación en qué orden se obtiene un proceso estacionario.
• El tercer parámetro q se refiere al orden de la parte de media móvil (MA) del modelo. Representa el número de errores de previsión retardados incluidos en el modelo. A diferencia de una media móvil simple, que suaviza los datos, la media móvil en ARIMA capta la relación entre una observación y los errores residuales de un modelo de media móvil aplicado a observaciones retardadas.

Encontrar los términos ARIMA

Utilizamos herramientas como la ACF (Función de Autocorrelación) y la PACF (Función de Autocorrelación Parcial) para determinar los valores de p, d y q. El número de rezagos en los que corta la ACF es q, y en los que corta la PACF es p. También tenemos que elegir el valor adecuado para dcreando una situación en la que, tras la diferenciación, los datos se parezcan al ruido blanco. Para nuestros datos, elegimos 1 tanto para p como para q porque observamos un pico significativo en el primer retardo de cada uno.

plot_acf(data["Price"], lags=40)
plot_pacf(data["Price"], lags=40)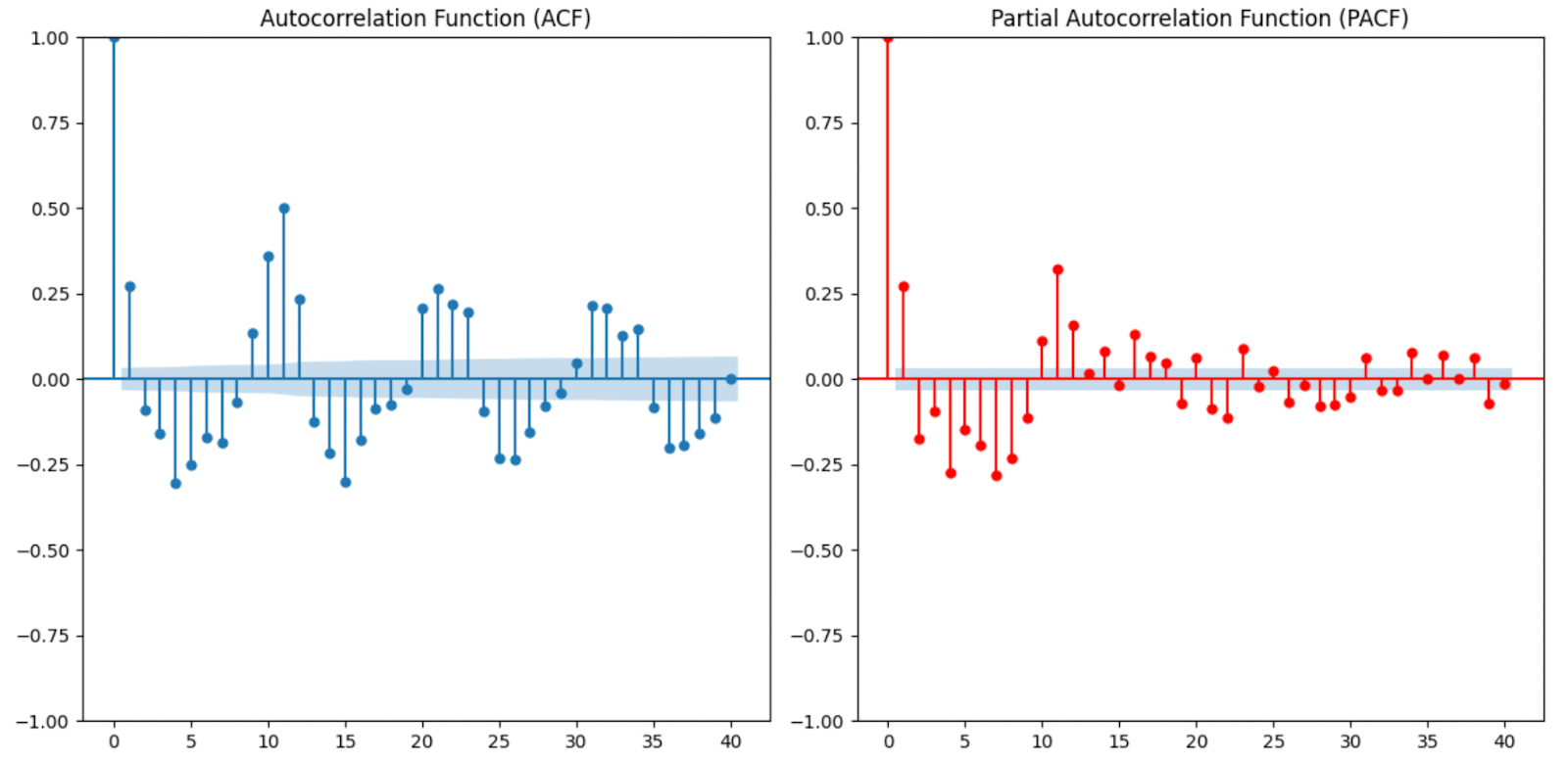

Gráficos ACF y PACF utilizados para determinar los términos ARIMA. Imagen del autor

Estimación de parámetros 

Para que quede claro, los valores p, d y q en ARIMA representan el orden del modelo (retardos para los términos de autorregresión, diferenciación y media móvil), pero no son los parámetros reales que se estiman. Una vez elegidos los valores p, d y q, el modelo estima los parámetros adicionales, como los coeficientes de los términos autorregresivos y de media móvil, mediante la Estimación de Máxima Verosimilitud (MLE).

Ajuste del modelo

# Fit the ARIMA model
# Initial ARIMA Model parameters
p, d, q = 1, 0, 1
model = ARIMA(data["Price"], order=(p, d, q))
model_fit = model.fit()
model_summary = model_fit.summary()
model_summary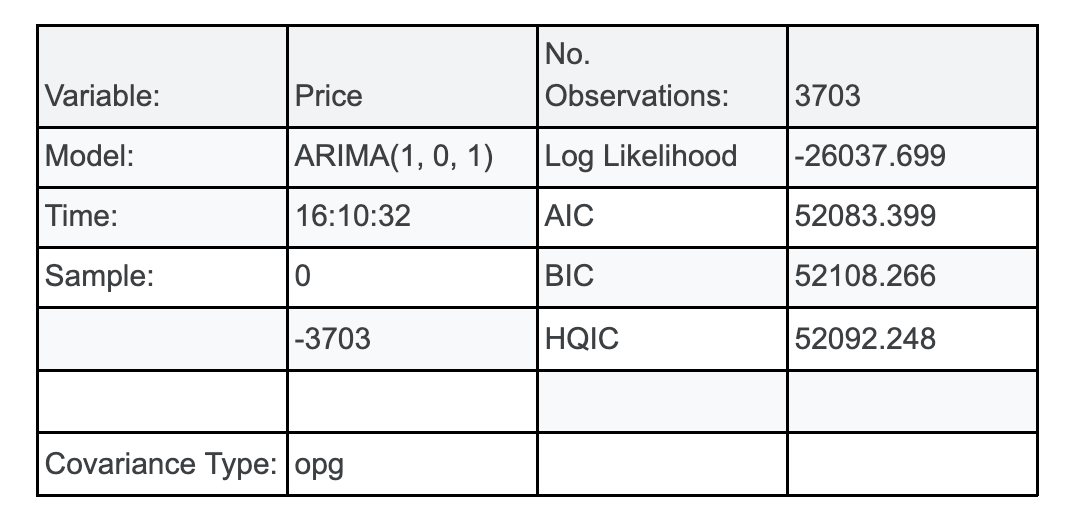

Estadísticas del modelo y diagnóstico del modelo

Ahora comprobamos los residuos y nos aseguramos de que actúan como ruido blanco, lo que significa que no deben tener patrones ni tendencias. Una opción es volver a utilizar nuestros gráficos ACF y PACF, pero esta vez aplicados a los residuos. Si en estos gráficos no hay grandes picos de retraso fuera de la banda, significa que nuestros residuos parecen ser ruido blanco. También podemos comprobar los residuos del modelo global para asegurarnos de que no hay patrones evidentes, como hacemos aquí:

Gráfico de residuos

# plot residual errors
residuals = model_fit.resid
residuals.plot()
residuals.plot(kind='kde')
plt.show()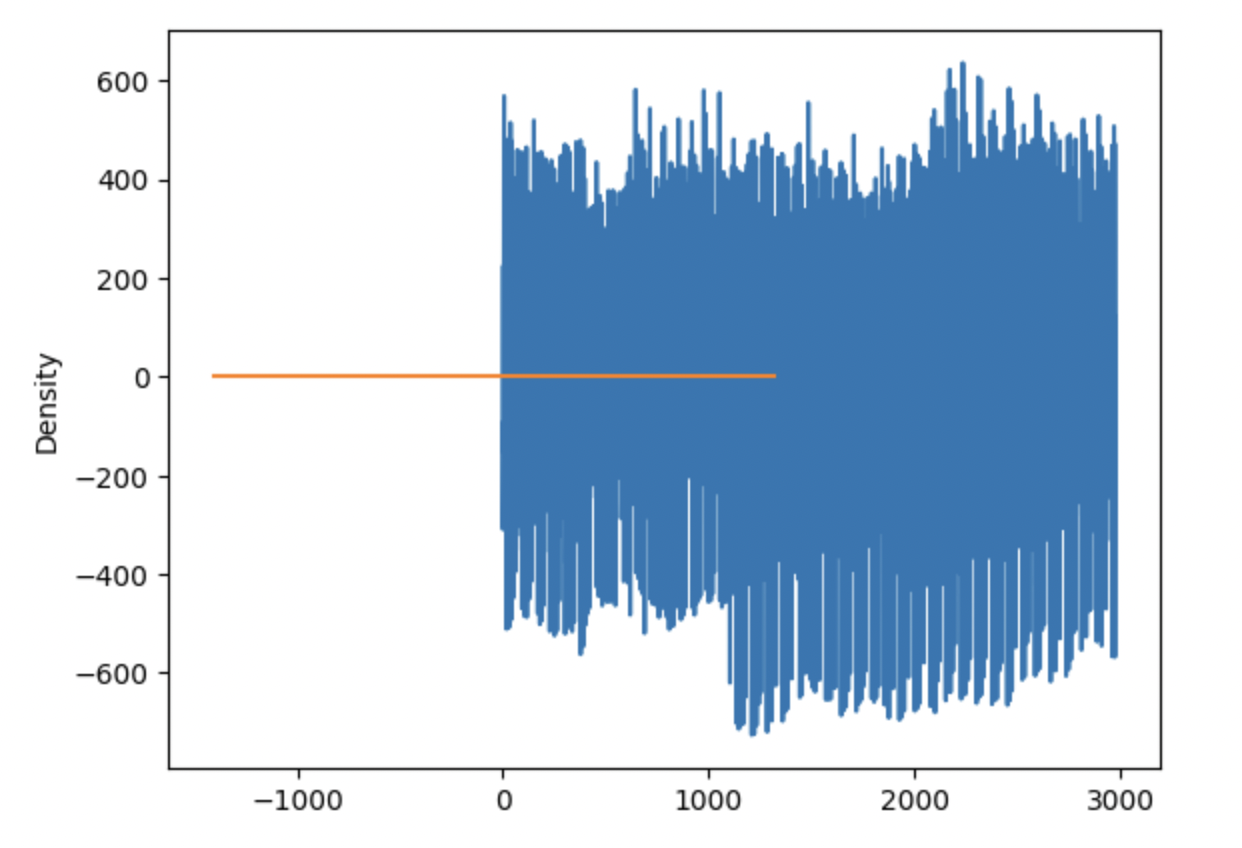

del modelo ARIMAResiduos del modelo ARIMA. Imagen del autor

AIC y BIC

Comprobamos las estadísticas del modelo relevantes para la selección del modelo. Los valores más bajos significan que el modelo se ajusta mejor, pero también podríamos comparar los resultados con los de modelos más sencillos para evitar el sobreajuste.

print(f"AIC: {model_fit.aic}")
print(f"BIC: {model_fit.bic}")

AIC: 41919.18902176751
BIC: 41937.18705062565

Previsión

Para pronosticar utilizando un modelo ARIMA, empieza utilizando el modelo ajustado para predecir los valores futuros basándote en los datos. Una vez hechas las predicciones, es útil visualizarlas trazando los valores predichos junto a los valores reales. Esto se consigue porque utilizamos un flujo de trabajo de entrenamiento/prueba, en el que los datos se dividen en conjuntos de entrenamiento y de prueba. Esto nos permite ver el rendimiento del modelo con datos no vistos. Nuestro curso Validación de Modelos en Python es un gran recurso para aprender los entresijos de la validación de modelos.

1. Utiliza un flujo de trabajo de entrenamiento/prueba

Nuestro primer paso es dividir los datos en versiones de entrenamiento y de prueba. 

data = data[“Price”]train_size = int(len(data) * 0.8)train, test = data[:train_size], data[train_size:]

# Fit the model to training data. Replace p, d, q with our ARIMA parameters
model = ARIMA(train_data["Price"], order=(p, d, q))  

# Forecast
forecast = model_fit.forecast(steps=len(test))

2. Visualizar nuestras series temporales

Nuestro siguiente paso es inspeccionar visualmente nuestra previsión de series temporales.

# Plotting
plt.figure(figsize=(10, 5))
plt.plot(data.index[:train_size], train, label='Train', color='blue')
plt.plot(data.index[train_size:], test, label='Test', color='green')
plt.plot(data.index[train_size:], forecast, label='Forecast', color='red')
plt.legend()
plt.title('ARIMA Forecast vs Actual')
plt.show()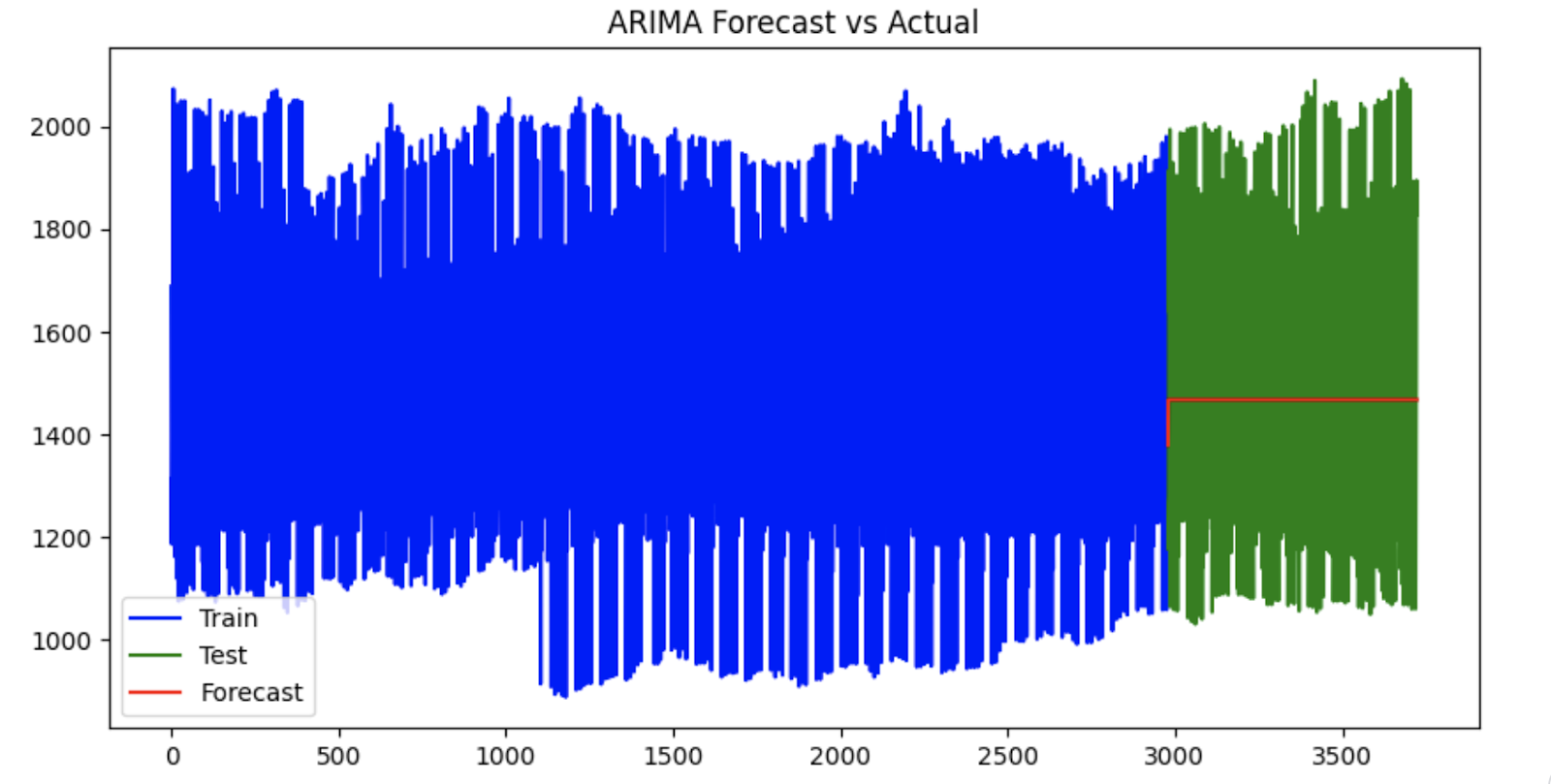

Previsión ARIMA valores reales frente a valores previstos. Imagen del autor

3. Evaluar las estadísticas del modelo

Evaluamos las estadísticas del modelo, en particular el error cuadrático medio, para valorar el ajuste de nuestro modelo. Un RMSE más bajo indica un modelo ARIMA mejor, que refleja menores diferencias entre los valores reales y los predichos.

# Evaluate model performance on the test set
rmse = mean_squared_error(test_data["Price"], predictions, squared=False)
print(f"RMSE: {rmse}")

“RMSE”: 135.87678712210163