Curso
Neste tutorial, você verá como usar um modelo de série temporal conhecido como Long Short-Term Memory. Os modelos LSTM são poderosos, especialmente para reter uma memória de longo prazo, por design, como você verá mais adiante. Você abordará os seguintes tópicos neste tutorial:
- Entenda por que você precisaria ser capaz de prever os movimentos dos preços das ações;
- Faça o download dos dados - Você usará dados do mercado de ações coletados do Yahoo Finance;
- Dividir os dados de treinamento-teste e também realizar alguma normalização dos dados;
- Examine e aplique algumas técnicas de cálculo de média que podem ser usadas para previsões de um passo à frente;
- Motive e discuta brevemente um modelo LSTM, pois ele permite prever com mais de uma etapa de antecedência;
- Prever e visualizar o mercado de ações futuro com dados atuais
Se não estiver familiarizado com a aprendizagem profunda ou com as redes neurais, dê uma olhada em nosso curso Aprendizagem profunda em Python. Ele aborda os conceitos básicos, além de como criar uma rede neural por conta própria no Keras. Esse é um pacote diferente do TensorFlow, que será usado neste tutorial, mas a ideia é a mesma.
Por que você precisa de modelos de séries temporais?
Você gostaria de modelar os preços das ações corretamente, de modo que, como comprador de ações, possa decidir razoavelmente quando comprar ações e quando vendê-las para obter lucro. É aí que entra a modelagem de séries temporais. Você precisa de bons modelos de aprendizado de máquina que possam analisar o histórico de uma sequência de dados e prever corretamente quais serão os elementos futuros da sequência.
Aviso: Os preços do mercado de ações são altamente imprevisíveis e voláteis. Isso significa que não há padrões consistentes nos dados que permitam modelar os preços das ações ao longo do tempo de forma quase perfeita. Não acredite em mim, acredite no economista da Universidade de Princeton, Burton Malkiel, que argumenta em seu livro de 1973, "A Random Walk Down Wall Street", que, se o mercado for realmente eficiente e o preço das ações refletir todos os fatores imediatamente assim que forem divulgados, um macaco de olhos vendados jogando dardos em uma listagem de ações de um jornal deve se sair tão bem quanto qualquer profissional de investimentos.
Entretanto, não vamos acreditar que esse é apenas um processo estocástico ou aleatório e que não há esperança para o aprendizado de máquina. Vamos ver se você consegue pelo menos modelar os dados, de modo que as previsões que você faz se correlacionem com o comportamento real dos dados. Em outras palavras, você não precisa dos valores exatos das ações no futuro, mas dos movimentos dos preços das ações (ou seja, se elas vão subir ou cair no futuro próximo).
# Make sure that you have all these libaries available to run the code successfully
from pandas_datareader import data
import matplotlib.pyplot as plt
import pandas as pd
import datetime as dt
import urllib.request, json
import os
import numpy as np
import tensorflow as tf # This code has been tested with TensorFlow 1.6
from sklearn.preprocessing import MinMaxScalerDownload dos dados
Você usará dados das seguintes fontes:
-
Alpha Vantage Stock API. Antes de começar, no entanto, você precisará primeiro de uma chave de API, que pode ser obtida gratuitamente aqui. Depois disso, você pode atribuir essa chave à variável
api_key. Neste tutorial, recuperaremos 20 anos de dados históricos das ações da American Airlines. Como leitura opcional, você pode consultar este guia inicial da API de ações para conhecer as práticas recomendadas de trabalho com dados históricos de mercado. -
Use os dados desta página. Você precisará copiar a pasta Stocks do arquivo zip para a pasta inicial do seu projeto.
Os preços das ações podem ser de vários tipos diferentes. São elas,
- Aberto: Preço de abertura da ação do dia
- Fechar: Preço de fechamento das ações do dia
- Alta: Preço mais alto das ações dos dados
- Baixo: Menor preço da ação do dia
Obtenção de dados do Alphavantage
Primeiro, você carregará os dados do Alpha Vantage. Como você usará os preços de mercado das ações da American Airlines para fazer suas previsões, defina o ticker como "AAL". Além disso, você também define um url_string, que retornará um arquivo JSON com todos os dados do mercado de ações da American Airlines nos últimos 20 anos, e um file_to_save, que será o arquivo no qual você salvará os dados. Você usará a variável ticker que definiu anteriormente para ajudar a nomear esse arquivo.
Em seguida, você especificará uma condição: se ainda não tiver salvado os dados, você irá em frente e pegará os dados do URL que definiu em url_string; Você armazenará os valores de data, baixa, alta, volume, fechamento e abertura em um DataFrame do pandas df e os salvará em file_to_save. No entanto, se os dados já estiverem lá, você simplesmente os carregará do CSV.
Obtendo dados do Kaggle
Os dados encontrados no Kaggle são uma coleção de arquivos csv e você não precisa fazer nenhum pré-processamento, portanto, pode carregar os dados diretamente em um Pandas DataFrame.
data_source = 'kaggle' # alphavantage or kaggle
if data_source == 'alphavantage':
# ====================== Loading Data from Alpha Vantage ==================================
api_key = '<your API key>'
# American Airlines stock market prices
ticker = "AAL"
# JSON file with all the stock market data for AAL from the last 20 years
url_string = "https://www.alphavantage.co/query?function=TIME_SERIES_DAILY&symbol=%s&outputsize=full&apikey=%s"%(ticker,api_key)
# Save data to this file
file_to_save = 'stock_market_data-%s.csv'%ticker
# If you haven't already saved data,
# Go ahead and grab the data from the url
# And store date, low, high, volume, close, open values to a Pandas DataFrame
if not os.path.exists(file_to_save):
with urllib.request.urlopen(url_string) as url:
data = json.loads(url.read().decode())
# extract stock market data
data = data['Time Series (Daily)']
df = pd.DataFrame(columns=['Date','Low','High','Close','Open'])
for k,v in data.items():
date = dt.datetime.strptime(k, '%Y-%m-%d')
data_row = [date.date(),float(v['3. low']),float(v['2. high']),
float(v['4. close']),float(v['1. open'])]
df.loc[-1,:] = data_row
df.index = df.index + 1
print('Data saved to : %s'%file_to_save)
df.to_csv(file_to_save)
# If the data is already there, just load it from the CSV
else:
print('File already exists. Loading data from CSV')
df = pd.read_csv(file_to_save)
else:
# ====================== Loading Data from Kaggle ==================================
# You will be using HP's data. Feel free to experiment with other data.
# But while doing so, be careful to have a large enough dataset and also pay attention to the data normalization
df = pd.read_csv(os.path.join('Stocks','hpq.us.txt'),delimiter=',',usecols=['Date','Open','High','Low','Close'])
print('Loaded data from the Kaggle repository')
Data saved to : stock_market_data-AAL.csv
Exploração de dados
Aqui você imprimirá os dados coletados no DataFrame. Você também deve se certificar de que os dados estejam classificados por data, pois a ordem dos dados é crucial na modelagem de séries temporais.
# Sort DataFrame by date
df = df.sort_values('Date')
# Double check the result
df.head()
| Data | Aberto | Alta | Baixa | Fechar | |
|---|---|---|---|---|---|
| 0 | 1970-01-02 | 0.30627 | 0.30627 | 0.30627 | 0.30627 |
| 1 | 1970-01-05 | 0.30627 | 0.31768 | 0.30627 | 0.31385 |
| 2 | 1970-01-06 | 0.31385 | 0.31385 | 0.30996 | 0.30996 |
| 3 | 1970-01-07 | 0.31385 | 0.31385 | 0.31385 | 0.31385 |
| 4 | 1970-01-08 | 0.31385 | 0.31768 | 0.31385 | 0.31385 |
Visualização de dados
Agora vamos ver que tipo de dados você tem. Você deseja dados com vários padrões que ocorrem ao longo do tempo.
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),(df['Low']+df['High'])/2.0)
plt.xticks(range(0,df.shape[0],500),df['Date'].loc[::500],rotation=45)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.show()
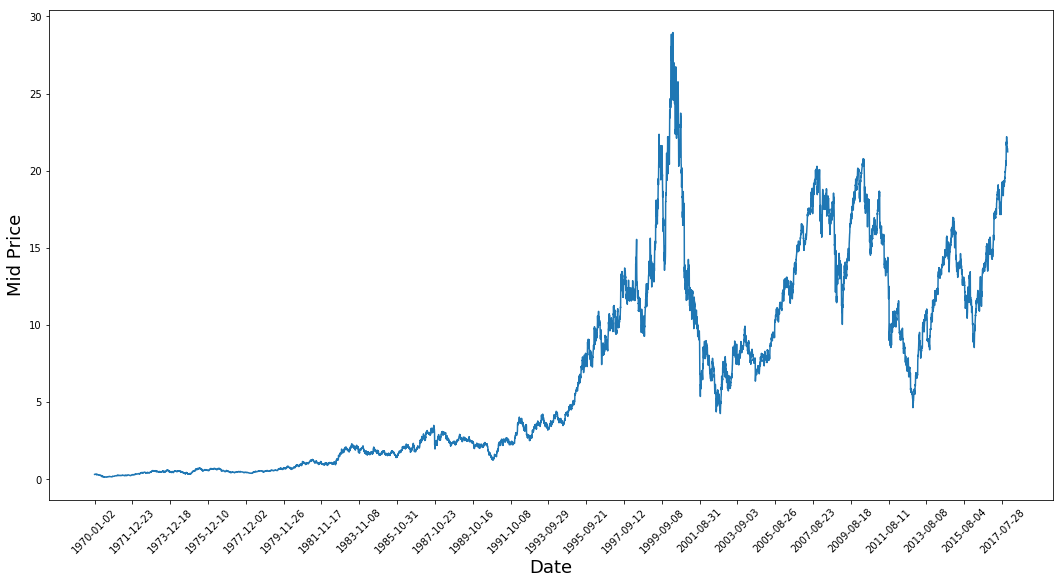
Esse gráfico já diz muitas coisas. O motivo específico pelo qual escolhi essa empresa em vez de outras é que esse gráfico está repleto de comportamentos diferentes dos preços das ações ao longo do tempo. Isso tornará o aprendizado mais robusto e lhe dará a oportunidade de testar a qualidade das previsões em diversas situações.
Outro aspecto a ser observado é que os valores próximos a 2017 são muito mais altos e flutuam mais do que os valores próximos à década de 1970. Portanto, você precisa se certificar de que os dados se comportem em intervalos de valores semelhantes durante todo o período de tempo. Você cuidará disso durante a fase de normalização dos dados.
Divisão de dados em um conjunto de treinamento e um conjunto de teste
Você usará o preço médio calculado pela média dos preços mais altos e mais baixos registrados em um dia.
# First calculate the mid prices from the highest and lowest
high_prices = df.loc[:,'High'].as_matrix()
low_prices = df.loc[:,'Low'].as_matrix()
mid_prices = (high_prices+low_prices)/2.0
Agora você pode dividir os dados de treinamento e os dados de teste. Os dados de treinamento serão os primeiros 11.000 pontos de dados da série temporal e o restante serão dados de teste.
train_data = mid_prices[:11000]
test_data = mid_prices[11000:]
Normalização dos dados
Agora você precisa definir um dimensionador para normalizar os dados. MinMaxScalar dimensiona todos os dados para que fiquem na região de 0 e 1. Você também pode remodelar os dados de treinamento e teste para que tenham a forma [data_size, num_features].
# Scale the data to be between 0 and 1
# When scaling remember! You normalize both test and train data with respect to training data
# Because you are not supposed to have access to test data
scaler = MinMaxScaler()
train_data = train_data.reshape(-1,1)
test_data = test_data.reshape(-1,1)
Devido à observação que você fez anteriormente, ou seja, diferentes períodos de tempo dos dados têm diferentes intervalos de valores, você normaliza os dados dividindo a série completa em janelas. Se você não fizer isso, os dados anteriores ficarão próximos de 0 e não agregarão muito valor ao processo de aprendizado. Aqui você escolhe um tamanho de janela de 2500.
Dica: ao escolher o tamanho da janela, certifique-se de que não seja muito pequeno, pois quando você executa a normalização em janelas, ela pode introduzir uma quebra no final de cada janela, já que cada janela é normalizada independentemente.
Neste exemplo, 4 pontos de dados serão afetados por isso. Mas como você tem 11.000 pontos de dados, 4 pontos não causarão nenhum problema
# Train the Scaler with training data and smooth data
smoothing_window_size = 2500
for di in range(0,10000,smoothing_window_size):
scaler.fit(train_data[di:di+smoothing_window_size,:])
train_data[di:di+smoothing_window_size,:] = scaler.transform(train_data[di:di+smoothing_window_size,:])
# You normalize the last bit of remaining data
scaler.fit(train_data[di+smoothing_window_size:,:])
train_data[di+smoothing_window_size:,:] = scaler.transform(train_data[di+smoothing_window_size:,:])
Remodelar os dados de volta à forma de [data_size]
# Reshape both train and test data
train_data = train_data.reshape(-1)
# Normalize test data
test_data = scaler.transform(test_data).reshape(-1)
Agora você pode suavizar os dados usando a média móvel exponencial. Isso ajuda você a se livrar da irregularidade inerente dos dados nos preços das ações e a produzir uma curva mais suave.
Observe que você só deve suavizar os dados de treinamento.
# Now perform exponential moving average smoothing
# So the data will have a smoother curve than the original ragged data
EMA = 0.0
gamma = 0.1
for ti in range(11000):
EMA = gamma*train_data[ti] + (1-gamma)*EMA
train_data[ti] = EMA
# Used for visualization and test purposes
all_mid_data = np.concatenate([train_data,test_data],axis=0)
Previsão de um passo à frente por meio de cálculo da média
Os mecanismos de média permitem que você faça previsões (geralmente um passo à frente) representando o preço futuro das ações como uma média dos preços das ações observados anteriormente. Fazer isso em mais de uma etapa de tempo pode produzir resultados bastante ruins. Você verá duas técnicas de cálculo de média abaixo: média padrão e média móvel exponencial. Você avaliará qualitativa (inspeção visual) e quantitativamente (erro quadrático médio) os resultados produzidos pelos dois algoritmos.
O erro quadrático médio (MSE) pode ser calculado considerando o erro quadrático entre o valor real em uma etapa anterior e o valor previsto e calculando a média de todas as previsões.
Média padrão
Você pode entender a dificuldade desse problema tentando primeiro modelá-lo como um problema de cálculo médio. Primeiro, você tentará prever os preços futuros do mercado de ações (por exemplo, xt+1 ) como uma média dos preços do mercado de ações observados anteriormente em uma janela de tamanho fixo (por exemplo, xt-N, ..., xt) (digamos, 100 dias anteriores). Depois disso, você tentará um método de "média móvel exponencial" um pouco mais sofisticado e verá como ele se sai. Em seguida, você passará para o "Santo Graal" da previsão de séries temporais: os modelos de memória de longo prazo.
Primeiro, você verá como funciona o cálculo normal da média. Ou seja, você diz,
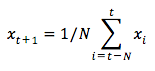
Em outras palavras, você diz que a previsão em $t+1$ é o valor médio de todos os preços de ações que você observou em uma janela de $t$ a $t-N$.
window_size = 100
N = train_data.size
std_avg_predictions = []
std_avg_x = []
mse_errors = []
for pred_idx in range(window_size,N):
if pred_idx >= N:
date = dt.datetime.strptime(k, '%Y-%m-%d').date() + dt.timedelta(days=1)
else:
date = df.loc[pred_idx,'Date']
std_avg_predictions.append(np.mean(train_data[pred_idx-window_size:pred_idx]))
mse_errors.append((std_avg_predictions[-1]-train_data[pred_idx])**2)
std_avg_x.append(date)
print('MSE error for standard averaging: %.5f'%(0.5*np.mean(mse_errors)))
MSE error for standard averaging: 0.00418
Dê uma olhada nos resultados médios abaixo. Ele segue de perto o comportamento real das ações. Em seguida, você verá um método de previsão de uma etapa mais preciso.
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),all_mid_data,color='b',label='True')
plt.plot(range(window_size,N),std_avg_predictions,color='orange',label='Prediction')
#plt.xticks(range(0,df.shape[0],50),df['Date'].loc[::50],rotation=45)
plt.xlabel('Date')
plt.ylabel('Mid Price')
plt.legend(fontsize=18)
plt.show()
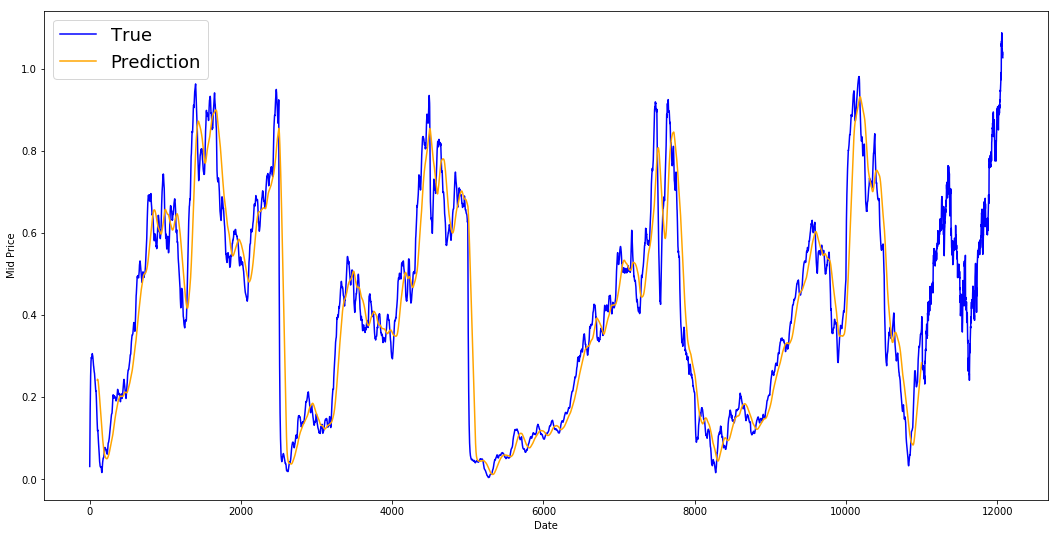
Então, o que dizem os gráficos acima (e o MSE)?
Parece que ele não é um modelo muito ruim para previsões muito curtas (um dia à frente). Considerando que os preços das ações não mudam de 0 para 100 da noite para o dia, esse comportamento é sensato. A seguir, você verá uma técnica de média mais sofisticada conhecida como média móvel exponencial.
Média Móvel Exponencial
Você já deve ter visto alguns artigos na Internet que usam modelos muito complexos e preveem o comportamento quase exato do mercado de ações. Mas cuidado! Essas são apenas ilusões de ótica e não se devem ao fato de aprender algo útil. Você verá abaixo como é possível replicar esse comportamento com um método simples de cálculo de média.
No método da média móvel exponencial, você calcula $x_{t+1}$ como,
- $x\_{t+1} = EMA\_{t} = \gamma \times EMA_{t-1} + (1-\gamma) x_t$ em que $EMA_0 = 0$ e $EMA$ é o valor da média móvel exponencial que você mantém ao longo do tempo.
A equação acima basicamente calcula a média móvel exponencial da etapa de tempo $t+1$ e a utiliza como previsão de uma etapa à frente. O $\gamma$ decide qual é a contribuição da previsão mais recente para a MME. Por exemplo, um $\gamma=0,1$ coloca apenas 10% do valor atual na MME. Como você pega apenas uma fração muito pequena da mais recente, isso permite preservar valores muito mais antigos que você viu muito cedo na média. Veja como isso fica bom quando usado para prever um passo à frente abaixo.
window_size = 100
N = train_data.size
run_avg_predictions = []
run_avg_x = []
mse_errors = []
running_mean = 0.0
run_avg_predictions.append(running_mean)
decay = 0.5
for pred_idx in range(1,N):
running_mean = running_mean*decay + (1.0-decay)*train_data[pred_idx-1]
run_avg_predictions.append(running_mean)
mse_errors.append((run_avg_predictions[-1]-train_data[pred_idx])**2)
run_avg_x.append(date)
print('MSE error for EMA averaging: %.5f'%(0.5*np.mean(mse_errors)))
MSE error for EMA averaging: 0.00003
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),all_mid_data,color='b',label='True')
plt.plot(range(0,N),run_avg_predictions,color='orange', label='Prediction')
#plt.xticks(range(0,df.shape[0],50),df['Date'].loc[::50],rotation=45)
plt.xlabel('Date')
plt.ylabel('Mid Price')
plt.legend(fontsize=18)
plt.show()
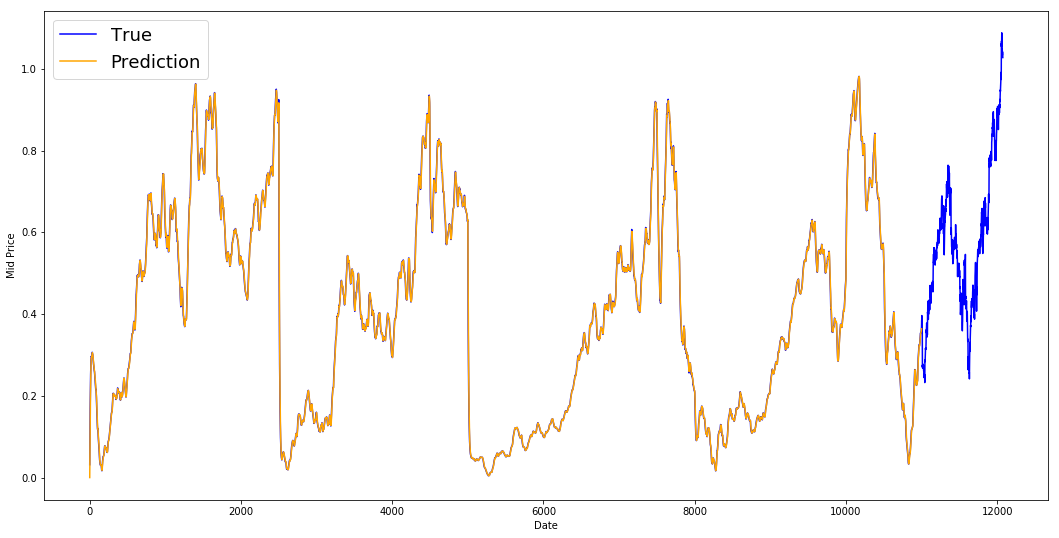
Se a média móvel exponencial é tão boa, por que você precisa de modelos melhores?
Você vê que ela se ajusta a uma linha perfeita que segue a distribuição True (e justificada pelo MSE muito baixo). Em termos práticos, você não pode fazer muita coisa apenas com o valor do mercado de ações do dia seguinte. Pessoalmente, o que eu gostaria de saber não é o preço exato do mercado de ações para o dia seguinte, mas se os preços do mercado de ações subiriam ou desceriam nos próximos 30 dias. Tente fazer isso e você exporá a incapacidade do método EMA.
Agora você tentará fazer previsões em janelas (digamos que você preveja a janela dos próximos 2 dias, em vez de apenas o dia seguinte). Então você perceberá como a EMA pode dar errado. Aqui está um exemplo:
Prever mais do que um passo no futuro
Para tornar as coisas concretas, vamos supor valores, digamos, $x_t=0,4$, $EMA=0,5$ e $\gamma = 0,5$
- Digamos que você obtenha a saída com a seguinte equação
- Xt+1 = EMAt = γ × EMAt-1 + (1 - γ)Xt
- Portanto, você tem xt+1 = 0,5 × 0,5 + (1-0,5) × 0,4 = 0,45
- So Xt+1 = EMAt = 0.45
- Portanto, a próxima previsão Xt+2 se torna,
- Xt+2 = γ × EMAt + (1-γ)Xt+1
- Ou seja, Xt+2 = γ × EMA_t + (1-γ) EMAt = EMAt
- Ou, neste exemplo, Xt+2 = Xt+1 = 0,45
Portanto, não importa quantas etapas você preveja no futuro, você continuará obtendo a mesma resposta para todas as etapas de previsão futura.
Uma solução que você tem e que produzirá informações úteis é examinar os algoritmos baseados em momentum. Eles fazem previsões com base no fato de os valores recentes passados estarem subindo ou descendo (não os valores exatos). Por exemplo, eles dirão que o preço do dia seguinte provavelmente será mais baixo, se os preços estiverem caindo nos últimos dias, o que parece razoável. No entanto, você usará um modelo mais complexo: um modelo LSTM.
Esses modelos tomaram de assalto o campo da previsão de séries temporais, porque são muito bons em modelar dados de séries temporais. Você verá se realmente há padrões ocultos nos dados que podem ser explorados.
Introdução aos LSTMs: Fazendo previsões de movimentação de ações em um futuro distante
Os modelos de memória de longo prazo são modelos de séries temporais extremamente avançados. Eles podem prever um número arbitrário de etapas no futuro. Um módulo (ou célula) LSTM tem 5 componentes essenciais que lhe permitem modelar dados de longo e curto prazo.
- Estado da célula (ct) - Representa a memória interna da célula, que armazena tanto a memória de curto prazo quanto as memórias de longo prazo
- Estado oculto (ht) - É a informação do estado de saída calculada com base na entrada atual, no estado oculto anterior e na entrada atual da célula, que você eventualmente usa para prever os preços futuros do mercado de ações. Além disso, o estado oculto pode decidir recuperar apenas os tipos de memória de curto, longo prazo ou ambos armazenados no estado da célula para fazer a próxima previsão.
- Porta de entrada (it) - Decide a quantidade de informações da entrada atual que flui para o estado da célula
- Porta de esquecimento (ft) - Decide a quantidade de informações da entrada atual e do estado anterior da célula que flui para o estado atual da célula
- Porta de saída (ot) - Decide a quantidade de informações do estado atual da célula que flui para o estado oculto, de modo que, se necessário, o LSTM só pode selecionar as memórias de longo prazo ou as memórias de curto prazo e as memórias de longo prazo.
Uma célula é mostrada na figura abaixo.
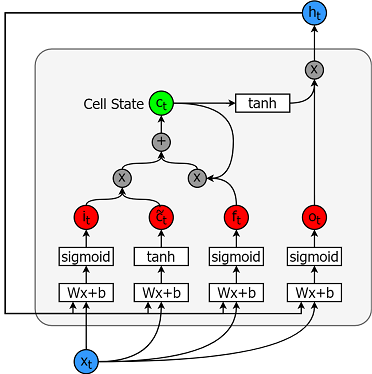
E as equações para calcular cada uma dessas entidades são as seguintes.
- it = σ(WixXt + Wihht-1 + bi)
- $\tilde{c}\_t = \sigma(W\_{cx}x\_t + W\_{ch}h_{t-1} + b_c)$
- $f\_t = \sigma(W\_{fx}x\_t + W\_{fh}h_{t-1}+b_f)$
- $c_t = f\_t c\_{t-1} + i_t \tilde{c}_t$
- $o\_t = \sigma(W\_{ox}x\_t + W\_{oh}h_{t-1}+b_o)$
- $h_t = o_t tanh(c_t)$
Para obter um entendimento melhor (mais técnico) sobre LSTMs, consulte este artigo.
O TensorFlow oferece uma boa subAPI (chamada API RNN) para implementar modelos de séries temporais. Você usará isso para suas implementações.
Gerador de dados
Primeiro, você implementará um gerador de dados para treinar seu modelo. Esse gerador de dados terá um método chamado .unroll_batches(...) que produzirá um conjunto de lotes num_unrollings de dados de entrada obtidos sequencialmente, em que um lote de dados tem o tamanho [batch_size, 1]. Assim, cada lote de dados de entrada terá um lote de dados de saída correspondente.
Por exemplo, se num_unrollings=3 e batch_size=4 um conjunto de lotes não rolados pode ter a seguinte aparência,
- dados de entrada: $[x_0,x_10,x_20,x_30], [x_1,x_11,x_21,x_31], [x_2,x_12,x_22,x_32]$
- dados de saída: $[x_1,x_11,x_21,x_31], [x_2,x_12,x_22,x_32], [x_3,x_13,x_23,x_33]$
Ampliação de dados
Além disso, para tornar seu modelo robusto, você não fará com que a saída para $x\_t$ seja sempre $x\_{t+1}$. Em vez disso, você fará uma amostragem aleatória de uma saída do conjunto $x\_{t+1},x\_{t+2},\ldots,x_{t+N}$, em que $N$ é um tamanho de janela pequeno.
Aqui você está fazendo a seguinte suposição:
- $x\_{t+1},x\_{t+2},\ldots,x_{t+N}$ não estarão muito distantes um do outro
Pessoalmente, acho que essa é uma suposição razoável para previsões de movimentação de ações.
Abaixo você ilustra como um lote de dados é criado visualmente.
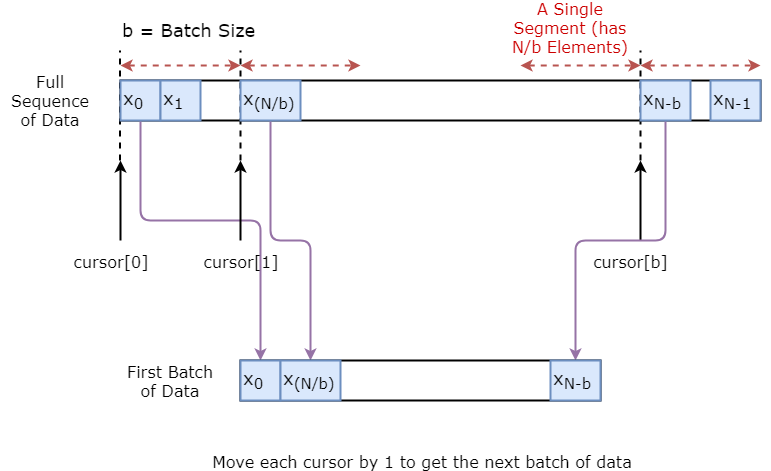
class DataGeneratorSeq(object):
def __init__(self,prices,batch_size,num_unroll):
self._prices = prices
self._prices_length = len(self._prices) - num_unroll
self._batch_size = batch_size
self._num_unroll = num_unroll
self._segments = self._prices_length //self._batch_size
self._cursor = [offset * self._segments for offset in range(self._batch_size)]
def next_batch(self):
batch_data = np.zeros((self._batch_size),dtype=np.float32)
batch_labels = np.zeros((self._batch_size),dtype=np.float32)
for b in range(self._batch_size):
if self._cursor[b]+1>=self._prices_length:
#self._cursor[b] = b * self._segments
self._cursor[b] = np.random.randint(0,(b+1)*self._segments)
batch_data[b] = self._prices[self._cursor[b]]
batch_labels[b]= self._prices[self._cursor[b]+np.random.randint(0,5)]
self._cursor[b] = (self._cursor[b]+1)%self._prices_length
return batch_data,batch_labels
def unroll_batches(self):
unroll_data,unroll_labels = [],[]
init_data, init_label = None,None
for ui in range(self._num_unroll):
data, labels = self.next_batch()
unroll_data.append(data)
unroll_labels.append(labels)
return unroll_data, unroll_labels
def reset_indices(self):
for b in range(self._batch_size):
self._cursor[b] = np.random.randint(0,min((b+1)*self._segments,self._prices_length-1))
dg = DataGeneratorSeq(train_data,5,5)
u_data, u_labels = dg.unroll_batches()
for ui,(dat,lbl) in enumerate(zip(u_data,u_labels)):
print('\n\nUnrolled index %d'%ui)
dat_ind = dat
lbl_ind = lbl
print('\tInputs: ',dat )
print('\n\tOutput:',lbl)
Unrolled index 0
Inputs: [0.03143791 0.6904868 0.82829314 0.32585657 0.11600105]
Output: [0.08698314 0.68685144 0.8329321 0.33355275 0.11785509]
Unrolled index 1
Inputs: [0.06067836 0.6890754 0.8325337 0.32857886 0.11785509]
Output: [0.15261841 0.68685144 0.8325337 0.33421066 0.12106793]
Unrolled index 2
Inputs: [0.08698314 0.68685144 0.8329321 0.33078218 0.11946969]
Output: [0.11098009 0.6848606 0.83387965 0.33421066 0.12106793]
Unrolled index 3
Inputs: [0.11098009 0.6858036 0.83294916 0.33219692 0.12106793]
Output: [0.132895 0.6836884 0.83294916 0.33219692 0.12288672]
Unrolled index 4
Inputs: [0.132895 0.6848606 0.833369 0.33355275 0.12158521]
Output: [0.15261841 0.6836884 0.83383167 0.33355275 0.12230608]
Definição de hiperparâmetros
Nesta seção, você definirá vários hiperparâmetros. D é a dimensionalidade da entrada. É simples, pois você usa o preço anterior da ação como entrada e prevê o próximo, que deve ser 1.
Em seguida, você tem num_unrollings, um hiperparâmetro relacionado à retropropagação através do tempo (BPTT) que é usado para otimizar o modelo LSTM. Isso indica quantas etapas de tempo contínuo você considera para uma única etapa de otimização. Você pode pensar nisso como, em vez de otimizar o modelo observando uma única etapa de tempo, você otimiza a rede observando num_unrollings etapas de tempo. Quanto maior, melhor.
Então você tem o batch_size. O tamanho do lote é o número de amostras de dados que você considera em uma única etapa de tempo.
Em seguida, defina num_nodes, que representa o número de neurônios ocultos em cada célula. Você pode ver que há três camadas de LSTMs neste exemplo.
D = 1 # Dimensionality of the data. Since your data is 1-D this would be 1
num_unrollings = 50 # Number of time steps you look into the future.
batch_size = 500 # Number of samples in a batch
num_nodes = [200,200,150] # Number of hidden nodes in each layer of the deep LSTM stack we're using
n_layers = len(num_nodes) # number of layers
dropout = 0.2 # dropout amount
tf.reset_default_graph() # This is important in case you run this multiple times
Definição de entradas e saídas
Em seguida, você define espaços reservados para entradas e rótulos de treinamento. Isso é muito simples, pois você tem uma lista de espaços reservados de entrada, em que cada espaço reservado contém um único lote de dados. E a lista tem num_unrollings espaços reservados, que serão usados de uma só vez para uma única etapa de otimização.
# Input data.
train_inputs, train_outputs = [],[]
# You unroll the input over time defining placeholders for each time step
for ui in range(num_unrollings):
train_inputs.append(tf.placeholder(tf.float32, shape=[batch_size,D],name='train_inputs_%d'%ui))
train_outputs.append(tf.placeholder(tf.float32, shape=[batch_size,1], name = 'train_outputs_%d'%ui))
Definição de parâmetros da camada LSTM e de regressão
Você terá três camadas de LSTMs e uma camada de regressão linear, denotadas por w e b, que obtêm a saída da última célula de memória de longo prazo e curto prazo e produzem a previsão para a próxima etapa de tempo. Você pode usar o MultiRNNCell no TensorFlow para encapsular os três objetos LSTMCell que você criou. Além disso, você pode ter as células LSTM implementadas com dropout, pois elas melhoram o desempenho e reduzem o excesso de ajuste.
lstm_cells = [
tf.contrib.rnn.LSTMCell(num_units=num_nodes[li],
state_is_tuple=True,
initializer= tf.contrib.layers.xavier_initializer()
)
for li in range(n_layers)]
drop_lstm_cells = [tf.contrib.rnn.DropoutWrapper(
lstm, input_keep_prob=1.0,output_keep_prob=1.0-dropout, state_keep_prob=1.0-dropout
) for lstm in lstm_cells]
drop_multi_cell = tf.contrib.rnn.MultiRNNCell(drop_lstm_cells)
multi_cell = tf.contrib.rnn.MultiRNNCell(lstm_cells)
w = tf.get_variable('w',shape=[num_nodes[-1], 1], initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable('b',initializer=tf.random_uniform([1],-0.1,0.1))
Calcular a saída do LSTM e alimentá-la na camada de regressão para obter a previsão final
Nesta seção, você primeiro cria variáveis do TensorFlow (c e h) que manterão o estado da célula e o estado oculto da célula de memória de longo prazo. Em seguida, você transforma a lista de train_inputs para ter a forma de [num_unrollings, batch_size, D], o que é necessário para calcular as saídas com a função tf.nn.dynamic_rnn. Em seguida, você calcula as saídas do LSTM com a função tf.nn.dynamic_rnn e divide a saída de volta em uma lista de tensores num_unrolling. a perda entre as previsões e os preços reais das ações.
# Create cell state and hidden state variables to maintain the state of the LSTM
c, h = [],[]
initial_state = []
for li in range(n_layers):
c.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
h.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
initial_state.append(tf.contrib.rnn.LSTMStateTuple(c[li], h[li]))
# Do several tensor transofmations, because the function dynamic_rnn requires the output to be of
# a specific format. Read more at: https://www.tensorflow.org/api_docs/python/tf/nn/dynamic_rnn
all_inputs = tf.concat([tf.expand_dims(t,0) for t in train_inputs],axis=0)
# all_outputs is [seq_length, batch_size, num_nodes]
all_lstm_outputs, state = tf.nn.dynamic_rnn(
drop_multi_cell, all_inputs, initial_state=tuple(initial_state),
time_major = True, dtype=tf.float32)
all_lstm_outputs = tf.reshape(all_lstm_outputs, [batch_size*num_unrollings,num_nodes[-1]])
all_outputs = tf.nn.xw_plus_b(all_lstm_outputs,w,b)
split_outputs = tf.split(all_outputs,num_unrollings,axis=0)
Cálculo e otimizador de perdas
Agora, você calculará a perda. No entanto, você deve observar que há uma característica única ao calcular a perda. Para cada lote de previsões e saídas reais, você calcula o erro quadrático médio. E você soma (não calcula a média) todas essas perdas quadráticas médias. Por fim, você define o otimizador que usará para otimizar a rede neural. Nesse caso, você pode usar o Adam, que é um otimizador muito recente e de bom desempenho.
# When calculating the loss you need to be careful about the exact form, because you calculate
# loss of all the unrolled steps at the same time
# Therefore, take the mean error or each batch and get the sum of that over all the unrolled steps
print('Defining training Loss')
loss = 0.0
with tf.control_dependencies([tf.assign(c[li], state[li][0]) for li in range(n_layers)]+
[tf.assign(h[li], state[li][1]) for li in range(n_layers)]):
for ui in range(num_unrollings):
loss += tf.reduce_mean(0.5*(split_outputs[ui]-train_outputs[ui])**2)
print('Learning rate decay operations')
global_step = tf.Variable(0, trainable=False)
inc_gstep = tf.assign(global_step,global_step + 1)
tf_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)
tf_min_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)
learning_rate = tf.maximum(
tf.train.exponential_decay(tf_learning_rate, global_step, decay_steps=1, decay_rate=0.5, staircase=True),
tf_min_learning_rate)
# Optimizer.
print('TF Optimization operations')
optimizer = tf.train.AdamOptimizer(learning_rate)
gradients, v = zip(*optimizer.compute_gradients(loss))
gradients, _ = tf.clip_by_global_norm(gradients, 5.0)
optimizer = optimizer.apply_gradients(
zip(gradients, v))
print('\tAll done')
Defining training Loss
Learning rate decay operations
TF Optimization operations
All done
Cálculos relacionados à previsão
Aqui você define as operações do TensorFlow relacionadas à previsão. Primeiro, defina um espaço reservado para alimentar a entrada (sample_inputs) e, em seguida, de forma semelhante ao estágio de treinamento, defina as variáveis de estado para a previsão (sample_c e sample_h). Por fim, você calcula a previsão com a função tf.nn.dynamic_rnn e, em seguida, envia a saída pela camada de regressão (w e b). Você também deve definir a operação reset_sample_state, que redefine o estado da célula e o estado oculto. Você deve executar essa operação no início, sempre que fizer uma sequência de previsões.
print('Defining prediction related TF functions')
sample_inputs = tf.placeholder(tf.float32, shape=[1,D])
# Maintaining LSTM state for prediction stage
sample_c, sample_h, initial_sample_state = [],[],[]
for li in range(n_layers):
sample_c.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
sample_h.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
initial_sample_state.append(tf.contrib.rnn.LSTMStateTuple(sample_c[li],sample_h[li]))
reset_sample_states = tf.group(*[tf.assign(sample_c[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)],
*[tf.assign(sample_h[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)])
sample_outputs, sample_state = tf.nn.dynamic_rnn(multi_cell, tf.expand_dims(sample_inputs,0),
initial_state=tuple(initial_sample_state),
time_major = True,
dtype=tf.float32)
with tf.control_dependencies([tf.assign(sample_c[li],sample_state[li][0]) for li in range(n_layers)]+
[tf.assign(sample_h[li],sample_state[li][1]) for li in range(n_layers)]):
sample_prediction = tf.nn.xw_plus_b(tf.reshape(sample_outputs,[1,-1]), w, b)
print('\tAll done')
Defining prediction related TF functions
All done
Executando o LSTM
Aqui você treinará e preverá movimentos de preços de ações para várias épocas e verá se as previsões melhoram ou pioram com o tempo. Você deve seguir o seguinte procedimento.
- Defina um conjunto de teste de pontos iniciais (
test_points_seq) na série temporal para avaliar o modelo - Para cada época
- Para o comprimento total da sequência de dados de treinamento
- Desenrole um conjunto de
num_unrollingslotes - Treinar a rede neural com os lotes não rolados
- Desenrole um conjunto de
- Calcular a perda média de treinamento
- Para cada ponto inicial no conjunto de teste
- Atualizar o estado do LSTM por meio da iteração dos pontos de dados anteriores
num_unrollingsencontrados antes do ponto de teste - Faça previsões para
n_predict_onceetapas continuamente, usando a previsão anterior como entrada atual - Calcule a perda de MSE entre os pontos
n_predict_onceprevistos e os preços reais das ações nesses momentos.
- Atualizar o estado do LSTM por meio da iteração dos pontos de dados anteriores
- Para o comprimento total da sequência de dados de treinamento
epochs = 30
valid_summary = 1 # Interval you make test predictions
n_predict_once = 50 # Number of steps you continously predict for
train_seq_length = train_data.size # Full length of the training data
train_mse_ot = [] # Accumulate Train losses
test_mse_ot = [] # Accumulate Test loss
predictions_over_time = [] # Accumulate predictions
session = tf.InteractiveSession()
tf.global_variables_initializer().run()
# Used for decaying learning rate
loss_nondecrease_count = 0
loss_nondecrease_threshold = 2 # If the test error hasn't increased in this many steps, decrease learning rate
print('Initialized')
average_loss = 0
# Define data generator
data_gen = DataGeneratorSeq(train_data,batch_size,num_unrollings)
x_axis_seq = []
# Points you start your test predictions from
test_points_seq = np.arange(11000,12000,50).tolist()
for ep in range(epochs):
# ========================= Training =====================================
for step in range(train_seq_length//batch_size):
u_data, u_labels = data_gen.unroll_batches()
feed_dict = {}
for ui,(dat,lbl) in enumerate(zip(u_data,u_labels)):
feed_dict[train_inputs[ui]] = dat.reshape(-1,1)
feed_dict[train_outputs[ui]] = lbl.reshape(-1,1)
feed_dict.update({tf_learning_rate: 0.0001, tf_min_learning_rate:0.000001})
_, l = session.run([optimizer, loss], feed_dict=feed_dict)
average_loss += l
# ============================ Validation ==============================
if (ep+1) % valid_summary == 0:
average_loss = average_loss/(valid_summary*(train_seq_length//batch_size))
# The average loss
if (ep+1)%valid_summary==0:
print('Average loss at step %d: %f' % (ep+1, average_loss))
train_mse_ot.append(average_loss)
average_loss = 0 # reset loss
predictions_seq = []
mse_test_loss_seq = []
# ===================== Updating State and Making Predicitons ========================
for w_i in test_points_seq:
mse_test_loss = 0.0
our_predictions = []
if (ep+1)-valid_summary==0:
# Only calculate x_axis values in the first validation epoch
x_axis=[]
# Feed in the recent past behavior of stock prices
# to make predictions from that point onwards
for tr_i in range(w_i-num_unrollings+1,w_i-1):
current_price = all_mid_data[tr_i]
feed_dict[sample_inputs] = np.array(current_price).reshape(1,1)
_ = session.run(sample_prediction,feed_dict=feed_dict)
feed_dict = {}
current_price = all_mid_data[w_i-1]
feed_dict[sample_inputs] = np.array(current_price).reshape(1,1)
# Make predictions for this many steps
# Each prediction uses previous prediciton as it's current input
for pred_i in range(n_predict_once):
pred = session.run(sample_prediction,feed_dict=feed_dict)
our_predictions.append(np.asscalar(pred))
feed_dict[sample_inputs] = np.asarray(pred).reshape(-1,1)
if (ep+1)-valid_summary==0:
# Only calculate x_axis values in the first validation epoch
x_axis.append(w_i+pred_i)
mse_test_loss += 0.5*(pred-all_mid_data[w_i+pred_i])**2
session.run(reset_sample_states)
predictions_seq.append(np.array(our_predictions))
mse_test_loss /= n_predict_once
mse_test_loss_seq.append(mse_test_loss)
if (ep+1)-valid_summary==0:
x_axis_seq.append(x_axis)
current_test_mse = np.mean(mse_test_loss_seq)
# Learning rate decay logic
if len(test_mse_ot)>0 and current_test_mse > min(test_mse_ot):
loss_nondecrease_count += 1
else:
loss_nondecrease_count = 0
if loss_nondecrease_count > loss_nondecrease_threshold :
session.run(inc_gstep)
loss_nondecrease_count = 0
print('\tDecreasing learning rate by 0.5')
test_mse_ot.append(current_test_mse)
print('\tTest MSE: %.5f'%np.mean(mse_test_loss_seq))
predictions_over_time.append(predictions_seq)
print('\tFinished Predictions')
Initialized
Average loss at step 1: 1.703350
Test MSE: 0.00318
Finished Predictions
...
...
...
Average loss at step 30: 0.033753
Test MSE: 0.00243
Finished Predictions
Visualizando as previsões
Você pode ver como a perda de MSE está diminuindo com a quantidade de treinamento. Isso é um bom sinal de que o modelo está aprendendo algo útil. Para quantificar suas descobertas, você pode comparar a perda de MSE da rede com a perda de MSE obtida ao fazer a média padrão (0,004). Você pode ver que o LSTM está se saindo melhor do que a média padrão. E você sabe que a média padrão (embora não seja perfeita) acompanhou razoavelmente os movimentos reais dos preços das ações.
best_prediction_epoch = 28 # replace this with the epoch that you got the best results when running the plotting code
plt.figure(figsize = (18,18))
plt.subplot(2,1,1)
plt.plot(range(df.shape[0]),all_mid_data,color='b')
# Plotting how the predictions change over time
# Plot older predictions with low alpha and newer predictions with high alpha
start_alpha = 0.25
alpha = np.arange(start_alpha,1.1,(1.0-start_alpha)/len(predictions_over_time[::3]))
for p_i,p in enumerate(predictions_over_time[::3]):
for xval,yval in zip(x_axis_seq,p):
plt.plot(xval,yval,color='r',alpha=alpha[p_i])
plt.title('Evolution of Test Predictions Over Time',fontsize=18)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.xlim(11000,12500)
plt.subplot(2,1,2)
# Predicting the best test prediction you got
plt.plot(range(df.shape[0]),all_mid_data,color='b')
for xval,yval in zip(x_axis_seq,predictions_over_time[best_prediction_epoch]):
plt.plot(xval,yval,color='r')
plt.title('Best Test Predictions Over Time',fontsize=18)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.xlim(11000,12500)
plt.show()
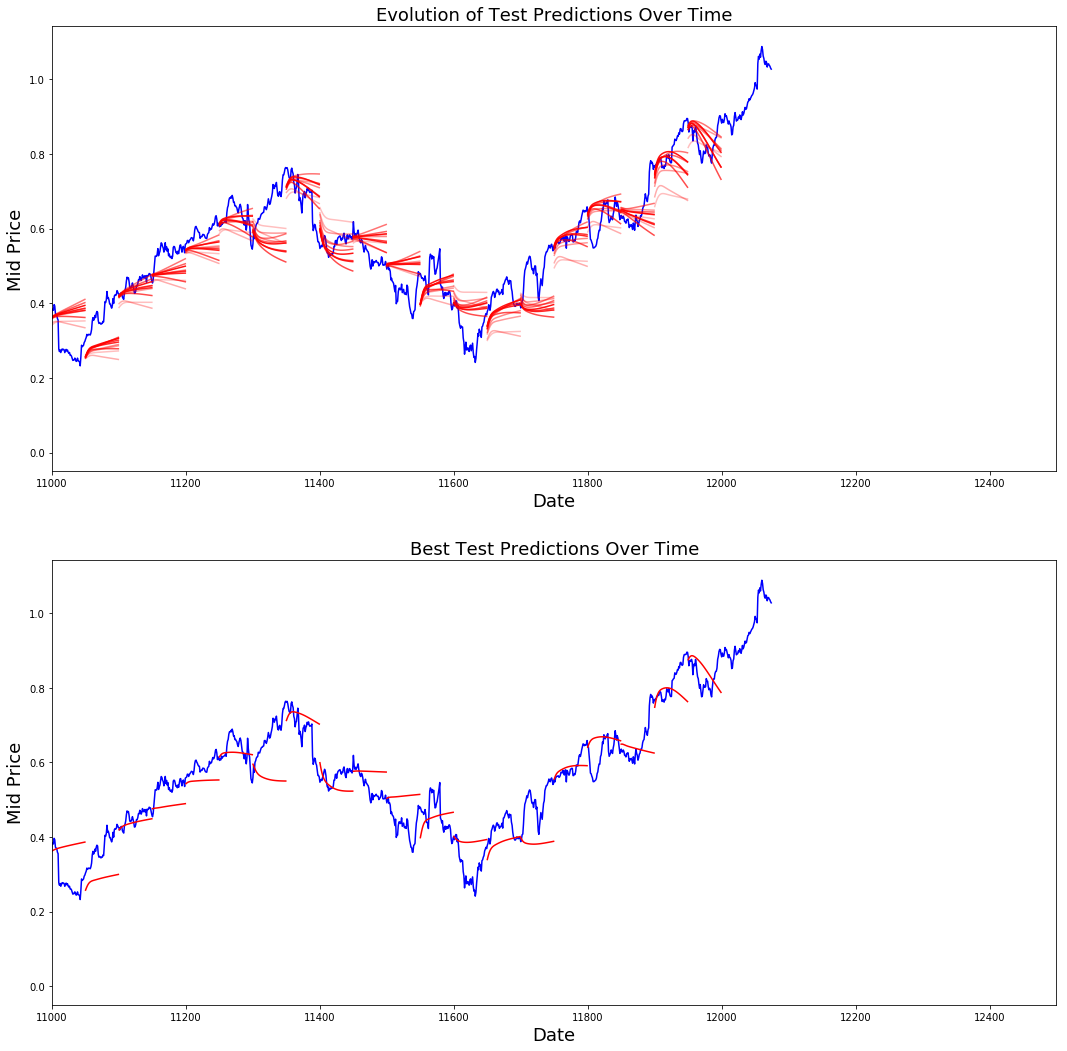
Embora não sejam perfeitos, os LSTMs parecem ser capazes de prever corretamente o comportamento do preço das ações na maior parte do tempo. Observe que você está fazendo previsões aproximadamente no intervalo de 0 e 1,0 (ou seja, não os preços reais das ações). Isso não tem problema, porque você está prevendo o movimento do preço das ações, não os preços em si.
Observações finais
Espero que este tutorial tenha sido útil para você. Devo mencionar que essa foi uma experiência gratificante para mim. Neste tutorial, aprendi como pode ser difícil criar um modelo capaz de prever corretamente os movimentos dos preços das ações. Você começou com uma motivação para a necessidade de modelar os preços das ações. Isso foi seguido por uma explicação e um código para o download de dados. Em seguida, você analisou duas técnicas de cálculo de média que permitem fazer previsões um passo à frente no futuro. Em seguida, você viu que esses métodos são inúteis quando é necessário prever mais de um passo no futuro. Depois disso, você discutiu como pode usar LSTMs para fazer previsões em várias etapas no futuro. Por fim, você visualizou os resultados e viu que seu modelo (embora não seja perfeito) é muito bom para prever corretamente os movimentos dos preços das ações.
Se quiser saber mais sobre aprendizagem profunda, não deixe de dar uma olhada em nosso curso Aprendizagem profunda em Python. Ele aborda os conceitos básicos, além de como criar uma rede neural por conta própria no Keras. Esse é um pacote diferente do TensorFlow, que será usado neste tutorial, mas a ideia é a mesma.
Aqui, estou apresentando várias conclusões deste tutorial.
-
A previsão do preço/movimento das ações é uma tarefa extremamente difícil. Pessoalmente, não acho que nenhum dos modelos de previsão de ações existentes no mercado deva ser considerado garantido e que não se deva confiar cegamente neles. Entretanto, os modelos podem ser capazes de prever corretamente o movimento do preço das ações na maior parte do tempo, mas nem sempre.
-
Não se deixe enganar por artigos que mostram curvas de previsão que se sobrepõem perfeitamente aos preços reais das ações. Isso pode ser replicado com uma técnica simples de cálculo de média e, na prática, é inútil. Uma coisa mais sensata a se fazer é prever os movimentos do preço das ações.
-
Os hiperparâmetros do modelo são extremamente sensíveis aos resultados que você obtém. Portanto, uma coisa muito boa a se fazer seria executar alguma técnica de otimização de hiperparâmetros (por exemplo, pesquisa em grade/pesquisa aleatória) nos hiperparâmetros. Abaixo, listo alguns dos hiperparâmetros mais críticos
- A taxa de aprendizado do otimizador
- Número de camadas e o número de unidades ocultas em cada camada
- O otimizador. Achei que o Adam teve o melhor desempenho
- Tipo de modelo. Você pode experimentar GRU/LSTM padrão/LSTM com Peepholes e avaliar a diferença de desempenho
-
Neste tutorial, você fez algo errado (devido ao tamanho pequeno dos dados)! Ou seja, você usou a perda do teste para decair a taxa de aprendizado. Isso vaza indiretamente informações sobre o conjunto de testes para o procedimento de treinamento. Uma maneira melhor de lidar com isso é ter um conjunto de validação separado (além do conjunto de teste) e diminuir a taxa de aprendizado em relação ao desempenho do conjunto de validação.
Se quiser entrar em contato comigo, envie-me um e-mail para thushv@gmail.com ou conecte-se a mim no LinkedIn.
Referências
Eu me referi a esse repositório para entender como usar LSTMs para previsões de ações. Mas os detalhes podem ser muito diferentes da implementação encontrada na referência.



