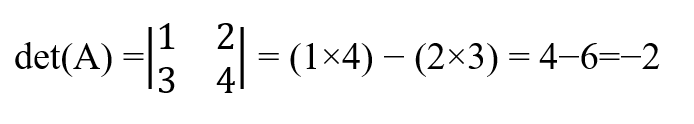O determinante: Como funciona e o que nos diz

As informações e os dados armazenados em uma arquitetura de computação estão na forma de matrizes. Portanto, por trás da maioria dos cálculos científicos e de machine learning estão matrizes de diferentes dimensões.

As matrizes são objetos matemáticos fundamentais na álgebra linear. As próprias matrizes têm algumas propriedades, como dimensão, esparsidade, valores próprios e determinantes.

Um determinante é uma propriedade fundamental de uma matriz quadrada que desempenha funções significativas, diretas e indiretas, em operações de matriz, como invertibilidade, solução de sistemas lineares em engenharia e transformações em geometria e computação gráfica.

Neste artigo, você aprenderá sobre os determinantes de uma matriz quadrada, suas aplicações e alguns métodos para calculá-los manualmente e com programas Python e R.

O que é um determinante?

Um determinante é uma função que mapeia uma matriz quadrada em um escalar real (valor único). Em matemática, o determinante de uma matriz quadrada A é mostrado como det(A) ou |A|.

Assim como a própria matemática, o determinante tem uma longa história que remonta aos matemáticos chineses. Na China antiga, os matemáticos usavam determinantes para resolver sistemas de equações lineares (seu método de resolução de equações lineares é hoje chamado de Regra de Cramer). Mais tarde, na Europa do século XVI, o matemático Cardano trouxe os determinantes à tona, aplicando-os na solução de sistemas de equações lineares. Mais tarde, Takakazu (século XVII), Leibniz (século XVII), Vandermonde e Cauchy (século XVIII) estabeleceram a base teórica dos determinantes na matemática pura.

Propriedades dos determinantes

Embora os determinantes precisem ser calculados para cada matriz quadrada, eles têm algumas propriedades conhecidas em geral e para algumas matrizes específicas. Além disso, os determinantes sujeitos a determinadas operações matemáticas também apresentam alguns padrões e propriedades. Algumas das propriedades conhecidas dos determinantes são as seguintes:

O determinante de uma matriz quadrada de identidade é 1

Uma matriz identidade tem valores de 1 na diagonal e 0 em outras partes.

Se você trocar duas linhas ou colunas, o sinal do determinante será alterado

Por exemplo, na matriz a seguir, o determinante é:

Se trocarmos as linhas, o resultado terá uma mudança de sinal.

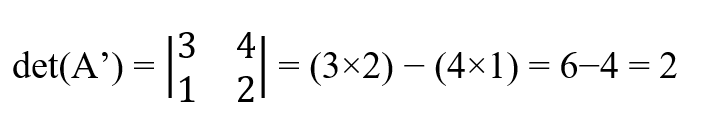
O determinante das matrizes triangulares é igual ao produto dos elementos diagonais

Se uma matriz for triangular inferior ou superior, para calcular o determinante, você só precisará multiplicar os valores diagonais. Por exemplo, na seguinte matriz quadrada triangular superior, o determinante é calculado pela multiplicação dos valores diagonais:

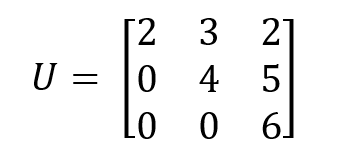
Basta multiplicar os elementos da diagonal para calcular o determinante: det(U)=2×4×6=48

O determinante é invariável sob a similaridade de matrizes

Duas matrizes são semelhantes se forem derivadas de uma transformação linear e tiverem bases diferentes. Se duas matrizes forem semelhantes, elas terão o mesmo determinante (e valores próprios, traços e polinômios característicos).

O determinante de um produto matricial é o produto dos determinantes das matrizes.

Como exemplo, os determinantes individuais das matrizes A e B são mostrados aqui:

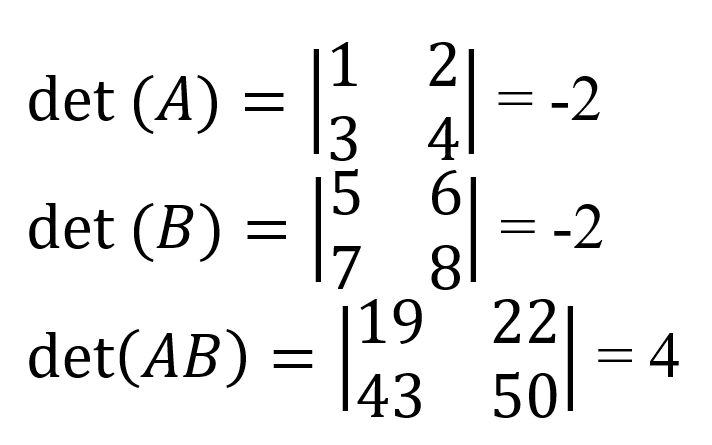
Os determinantes são invariantes sob transposição

Por exemplo, o determinante da matriz A e AT é o mesmo (-9).

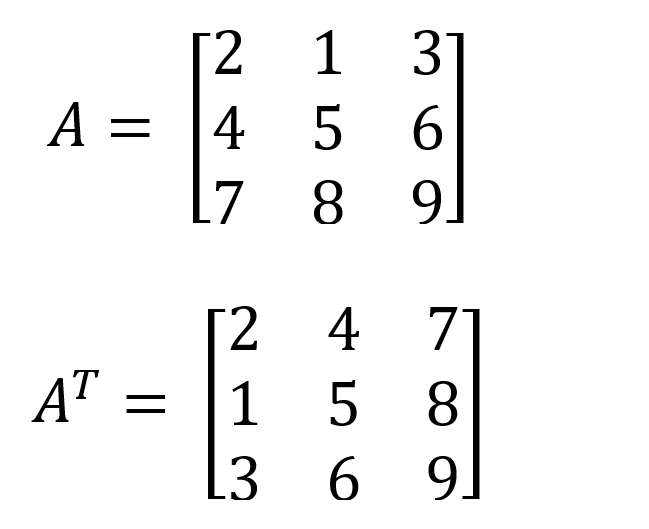
Métodos de cálculo de determinantes

Há diferentes métodos para calcular o determinante de uma matriz quadrada, como a fórmula de Leibniz, a expansão de Laplace e a eliminação gaussiana. A escolha do método está sujeita ao tamanho da matriz e aos custos de computação. A seguir, descrevemos alguns desses métodos:

Fórmula de Leibniz

A fórmula de Leibniz para encontrar o determinante de uma matriz quadrada é mais adequada para matrizes pequenas, especialmente se o cálculo for feito total ou parcialmente à mão. A fórmula de Leibniz para encontrar o determinante de uma matriz é a seguinte:

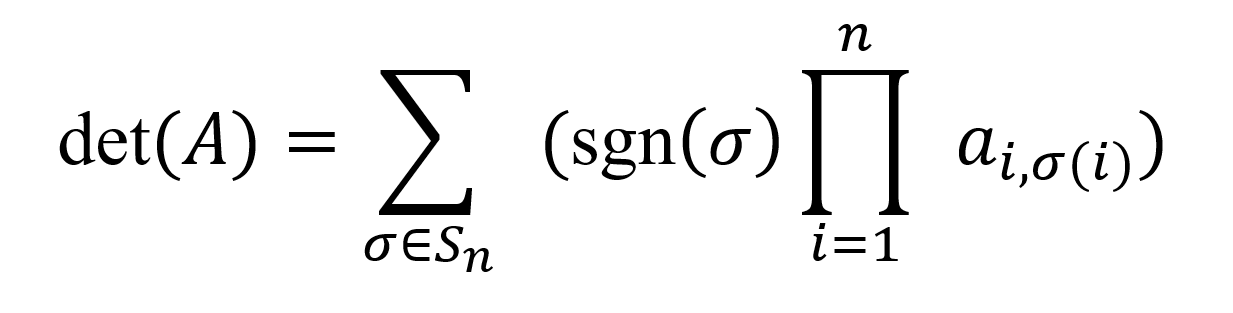
Onde Sn denota o conjunto de todas as permutações dos números 1,2,...,n e sgn(σ)é o sinal da permutação, que é +1 se a permutação for par e -1 se a permutação for ímpar. O termo ai,σ é um elemento da matriz A.

Expansão de Laplace

Expansão de Laplace é ideal para matrizes maiores. Na expansão de Laplace ou de cofator, uma matriz grande é dividida em matrizes menores. Em seguida, um esquema que envolve o determinante (menor) de uma matriz menor e seu cofator é projetado e iterado em linhas ou colunas.

Eliminação gaussiana

Como o determinante de uma matriz triangular é o produto de seus elementos diagonais, a redução de uma matriz a uma matriz diagonal torna o cálculo do determinante mais eficiente. Na eliminação gaussiana, uma série de operações de linha é realizada para reduzir a matriz completa ao escalonamento de linhas ou à forma triangular superior. Em seguida, o determinante é calculado pela multiplicação dos elementos diagonais.

Como encontrar o determinante para matrizes de tamanhos diferentes

Nos exemplos a seguir, aplicamos cada um dos métodos anteriores a matrizes de tamanhos diferentes para encontrar os determinantes.

Como encontrar o determinante de uma matriz 2x2

O determinante de uma matriz quadrada 2x2 é o mais fácil de lembrar e calcular. Se denotarmos uma matriz 2x2 A como: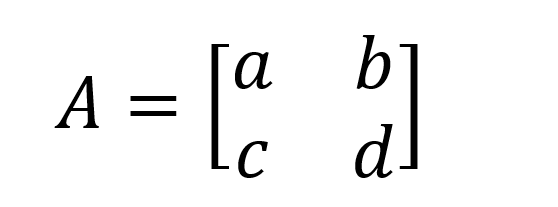 

Então det(A) = (a x d) - (b x c). Por exemplo, para a matriz B abaixo:

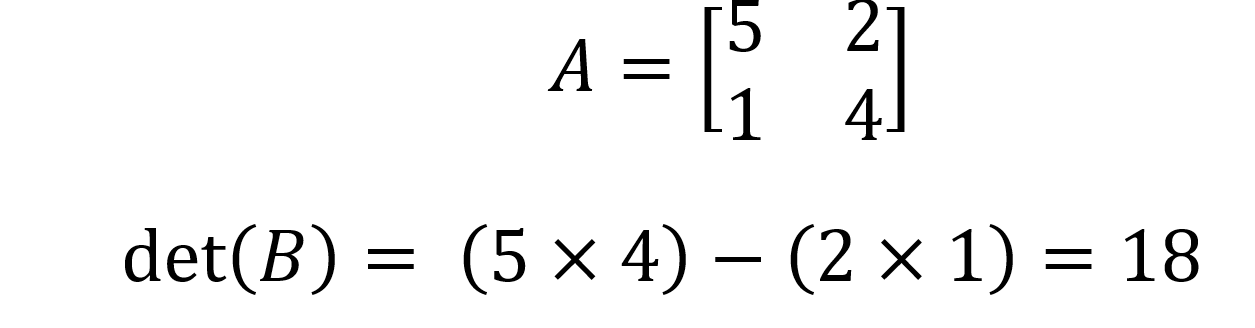
Como encontrar o determinante de uma matriz 3x3

Embora exista uma fórmula para o cálculo de uma matriz quadrada 3x3, por motivos pedagógicos, demonstramos a expansão de Laplace (cofator) neste exemplo. A seguir, calcularemos o determinante da matriz A:

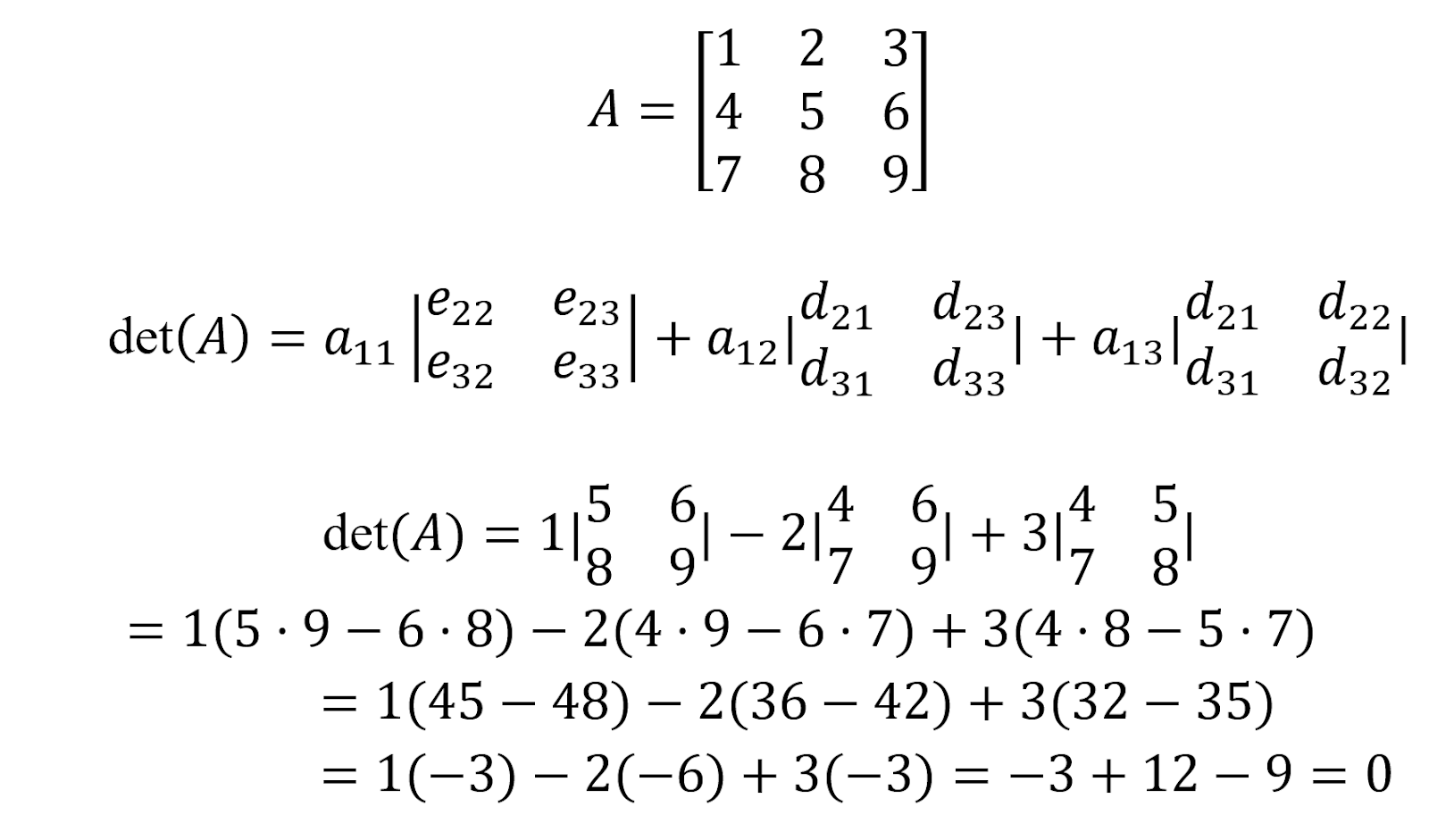
Como encontrar o determinante de uma matriz 4x4

Agora, aproveitamos a oportunidade para mostrar o método de eliminação gaussiana para calcular o determinante de uma matriz 4 x 4 A abaixo: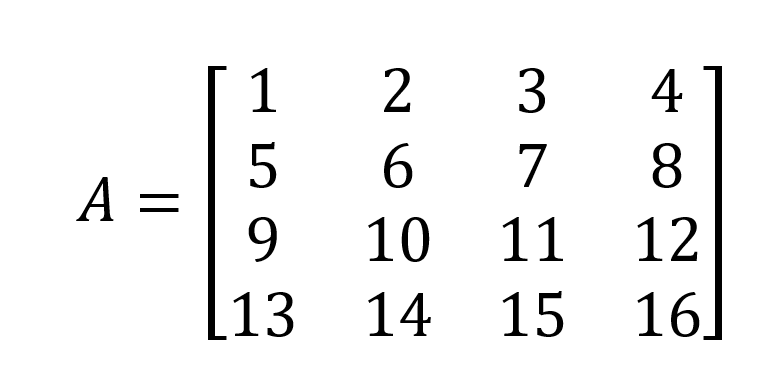

Transformaremos essa matriz em uma matriz triangular superior realizando operações de linha.

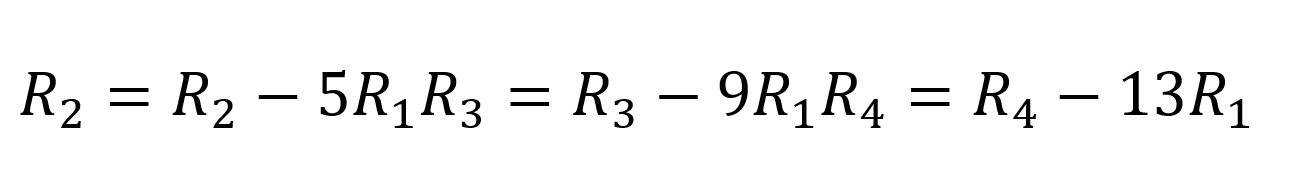
Temos,

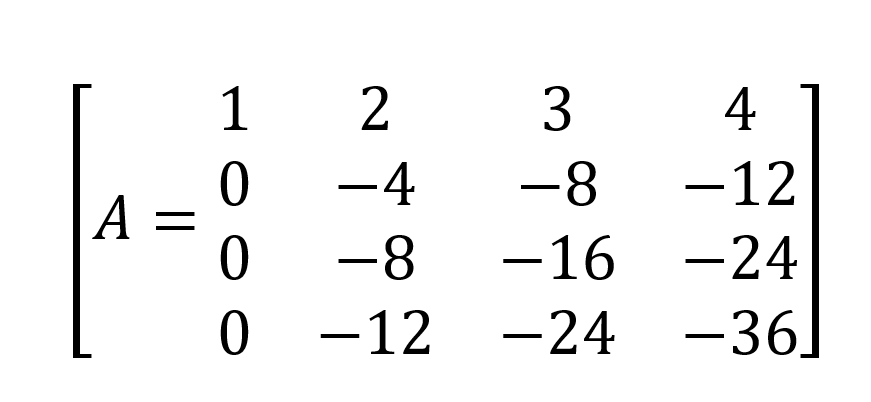
Mais uma operação de linha:

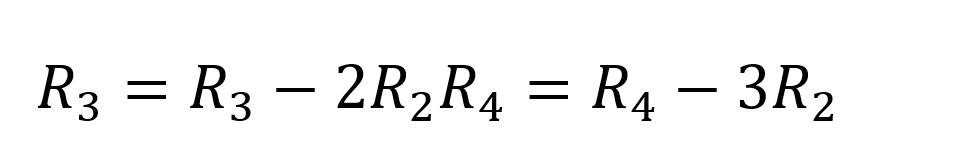
Temos, 

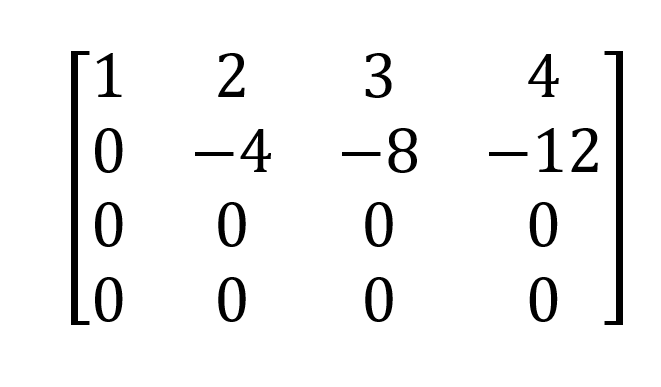
E o determinante é o produto dos elementos diagonais:

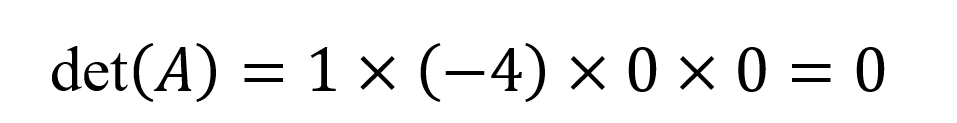
Significado geométrico e algébrico

Como definimos acima, um determinante é uma função que mapeia uma matriz quadrada para um número real.

Na geometria, um quadrado consiste em dois lados, cujo produto é a área da superfície. E se houver três lados, você obterá o volume. O (valor absoluto do) determinante de uma matriz 2 x 2 pode ser interpretado como a área de um paralelogramo formado pelas duas colunas da matriz (como vetores direcionais), e o determinante assinado de uma matriz 3 x 3 pode ser interpretado como o volume de um paralelepípedo (sólido tridimensional).

Em transformações gráficas, como esticar ou encolher uma imagem, o determinante da imagem transformada mostra se a área da imagem original (matriz) foi alterada ou não (princípio de Cavalieri) após a transformação, enquanto os valores próprios mostram se a imagem foi ampliada ou encolhida com ou sem alteração da área.

Os determinantes também podem indicar se as colunas ou linhas de uma matriz são combinações lineares umas das outras (redundância) ou se são linearmente independentes, cada uma com informações exclusivas. Se o determinante de uma matriz for diferente de zero, concluímos que as colunas ou linhas da matriz são linearmente independentes. Se o determinante for zero, isso mostra que as colunas (ou linhas) da matriz são linearmente dependentes.

Por fim, os determinantes também são usados na formulação do polinômio característico para calcular os valores próprios.

O determinante em Python e R

Embora o cálculo manual de determinantes seja uma experiência de aprendizado valiosa para aprimorar nossas habilidades matemáticas e desenvolver sofisticação matemática, eventualmente as restrições de tempo e energia podem nos fazer usar uma calculadora ou uma linguagem de programação, como Python ou R. Tanto o Python quanto o R fornecem bibliotecas, funções ou métodos para calcular o determinante de uma matriz. Nos trechos de código a seguir, demonstramos como você pode calcular o determinante de uma matriz usando Python e R.

Exemplo em Python

Dois pacotes populares do Python para calcular o determinante de uma matriz incluem o Numpy e o Sympy (Symbolic Python). No trecho de código a seguir, mostramos como você pode calcular o determinante usando as bibliotecas Numpy e Sympy em Python.

# Computing determinant using Numpy
import numpy as np
matrix = np.array([[1, 2], [3, 4]])
determinant = np.linalg.det(matrix)
print("Determinant:", determinant)
 
# Computing determinant using Sympy# Import the necessary library
import sympy as sp
matrix = sp.Matrix([[1, 2], [3, 4]])
determinant = matrix.det()
print("Determinant:", determinant)
 

Exemplo de R

Para calcular o determinante de uma matriz no R, você não precisa carregar uma biblioteca. O R básico fornece uma função integrada para calcular o determinante de uma matriz, conforme mostrado no trecho de código do R a seguir:

matrix <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
determinant <- det(matrix)
print(paste("Determinant:", determinant))

Aplicações de determinantes

Sistemas lineares

Os determinantes podem ser usados diretamente na solução de um sistema de equações lineares usando a regra de Cramer. Pela regra de Cramer, primeiro construímos uma matriz que consiste nos coeficientes das incógnitas no sistema de equações e calculamos seu determinante. Em seguida, formamos uma matriz para cada incógnita e calculamos seu determinante. A razão entre o determinante da nova matriz e a matriz principal será o valor da incógnita.

Equações diferenciais

Uma equação diferencial pode ter várias soluções (funções). Para garantir que as soluções sejam linearmente independentes (únicas), são calculados os determinantes do conjunto de soluções da função, chamados de Wronskian. Um Wronskian diferente de zero indica que as funções/soluções são linearmente independentes no intervalo determinado.

Geometria

Na geometria, o determinante de uma matriz 2 x 2 pode ser interpretado como a área de um paralelogramo, e o determinante de uma matriz 3 x 3 pode ser interpretado como o volume de um sólido (paralelepípedo).  Os determinantes no mapeamento de funções multivariáveis podem ajudar você a entender se o mapeamento afetou a área ou o volume das funções usando o determinante da matriz Jacobiana.

Pontos-chave a serem lembrados

Os determinantes desempenham uma função mais indireta em machine learning, estatística e computação científica. No entanto, entender como o sistema de equações lineares, a inversão de matrizes, a computação gráfica e as equações diferenciais usam determinantes no processo pode esclarecer seu significado sutil e a necessidade de entender os determinantes. Da próxima vez que encontrar um erro de matriz invertível, você pode pensar sobre o papel do determinante na forma e na independência linear da matriz.

Conclusão

Espero que você tenha percebido como o determinante é importante para entender o comportamento e as transformações da matriz. Nosso curso Álgebra linear para ciência de dados em R é uma ótima próxima etapa para você continuar aprendendo técnicas de álgebra linear e aplicar as técnicas em fluxos de trabalho de ciência de dados.