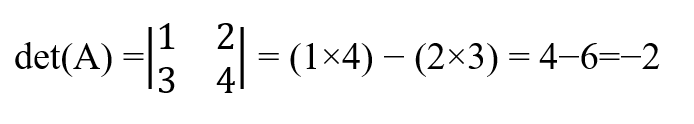Cours
Les informations et les données stockées sur une architecture informatique se présentent sous la forme de matrices. C'est pourquoi, dans la plupart des domaines scientifiques, de l'apprentissage automatique et des calculs, on trouve des matrices de différentes dimensions.
Les matrices sont des objets mathématiques fondamentaux en algèbre linéaire. Les matrices elles-mêmes ont certaines propriétés, telles que la dimension, l'éparpillement, les valeurs propres et les déterminants.
Un déterminant est une propriété fondamentale d'une matrice carrée qui joue un rôle direct et indirect important dans les opérations matricielles, telles que l'inversibilité, la résolution de systèmes linéaires en ingénierie et les transformations en géométrie et en infographie.
Dans cet article, vous découvrirez les déterminants d'une matrice carrée, leurs applications et quelques méthodes pour les calculer à la main et avec des programmes Python et R.
Qu'est-ce qu'un déterminant ?
Un déterminant est une fonction qui fait correspondre une matrice carrée à un scalaire réel (une seule valeur). En mathématiques, le déterminant d'une matrice carrée A est représenté par det(A) ou |A|.
Comme les mathématiques elles-mêmes, le déterminant a une longue histoire qui remonte aux mathématiciens chinois. Dans la Chine ancienne, les mathématiciens utilisaient les déterminants pour résoudre les systèmes d'équations linéaires (leur méthode de résolution des équations linéaires est aujourd'hui appelée règle de Cramer). Plus tard, au XVIe siècle en Europe, le mathématicien Cardano a mis les déterminants à l'honneur en les appliquant à la résolution de systèmes d'équations linéaires. Plus tard, Takakazu (17e siècle), Leibniz (17e siècle), Vandermonde et Cauchy (18e siècle) ont établi les fondements théoriques des déterminants en mathématiques pures.
Propriétés des déterminants
Bien que les déterminants doivent être calculés pour chaque matrice carrée, ils possèdent certaines propriétés connues en général et pour certaines matrices spécifiques. En outre, les déterminants soumis à certaines opérations mathématiques présentent également certaines caractéristiques et propriétés. Voici quelques-unes des propriétés bien connues des déterminants :
Le déterminant d'une matrice identité carrée est 1
Une matrice d'identité a des valeurs de 1 sur la diagonale et de 0 ailleurs.
L'interversion de deux lignes ou colonnes modifie le signe du déterminant.
Par exemple, dans la matrice suivante, le déterminant est :
Si nous intervertissons les lignes, le résultat change de signe.
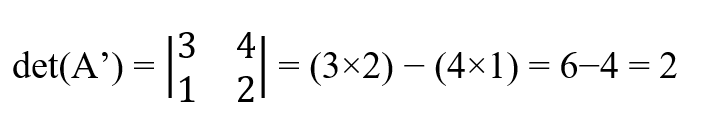
Le déterminant des matrices triangulaires est égal au produit des éléments diagonaux
Si une matrice est triangulaire inférieure ou supérieure, il suffit de multiplier les valeurs diagonales pour calculer le déterminant. Par exemple, dans la matrice carrée triangulaire supérieure suivante, le déterminant est calculé en multipliant les valeurs diagonales :
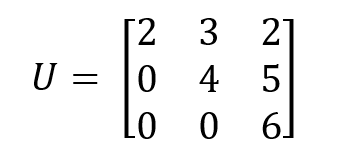
Il suffit de multiplier les éléments diagonaux pour calculer le déterminant : det(U)=2×4×6=48
Le déterminant est invariant sous l'effet de la similarité des matrices
Deux matrices sont similaires si elles sont dérivées d'une transformation linéaire et ont des bases différentes. Si deux matrices sont similaires, elles ont le même déterminant (ainsi que les valeurs propres, les traces et les polynômes caractéristiques).
Le déterminant d'un produit matriciel est le produit des déterminants des matrices.
A titre d'exemple, les déterminants individuels des matrices A et B sont présentés ici :
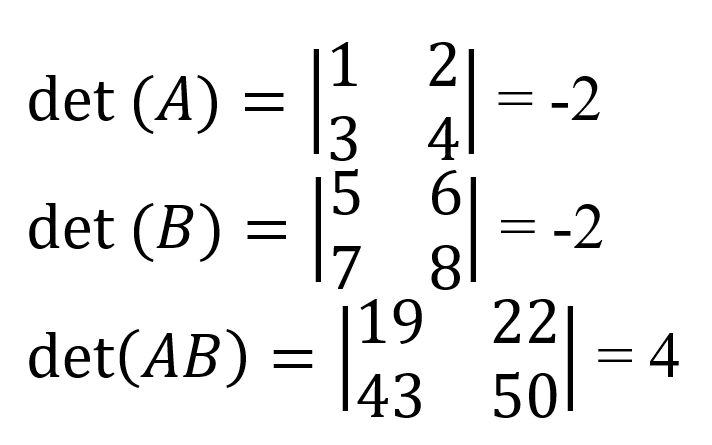
Les déterminants sont invariants par transposition
Par exemple, le déterminant de la matrice A et AT est le même (-9).
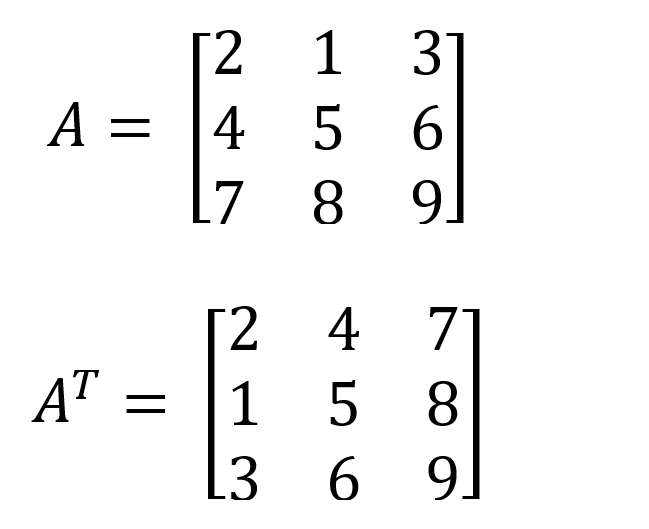
Méthodes de calcul des déterminants
Il existe différentes méthodes pour calculer le déterminant d'une matrice carrée, telles que la formule de Leibniz, le développement de Laplace et l'élimination de Gauss. Le choix de la méthode dépend de la taille de la matrice et des coûts de calcul. Nous décrivons ci-dessous certaines de ces méthodes :
Leibniz formula
La formule de Leibniz pour trouver le déterminant d'une matrice carrée convient mieux aux petites matrices, surtout si le calcul est effectué entièrement ou en partie à la main. La formule de Leibniz pour trouver le déterminant d'une matrice est la suivante :
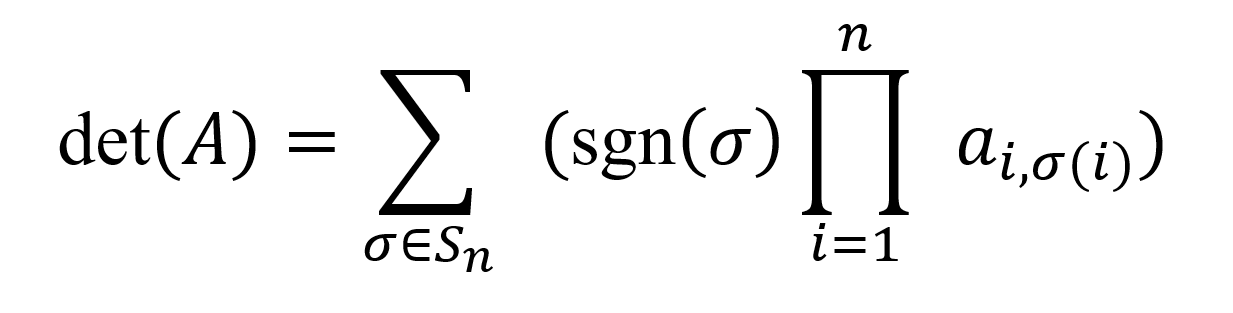
Où Sn désigne l'ensemble de toutes les permutations des nombres 1,2,...,n et sgn(σ)est le signe de la permutation, qui est +1 si la permutation est paire et -1 si la permutation est impaire. Le terme ai,σ est un élément de la matrice A.
Développement de Laplace
L'expansion de Laplace est idéale pour les grandes matrices. Dans l'expansion de Laplace ou cofacteur, une grande matrice est divisée en matrices plus petites. Ensuite, un schéma impliquant le déterminant (mineur) d'une matrice plus petite et son cofacteur est conçu et itéré sur les lignes ou les colonnes.
Élimination de la gaussienne
Le déterminant d'une matrice triangulaire étant le produit de ses éléments diagonaux, la réduction d'une matrice à une matrice diagonale rend le calcul du déterminant plus efficace. Dans l'élimination gaussienne, une série d'opérations sur les lignes est effectuée pour réduire la matrice complète à l'échelon des lignes ou à la forme triangulaire supérieure. Le déterminant est ensuite calculé en multipliant les éléments diagonaux.
Comment trouver le déterminant pour des matrices de tailles différentes ?
Dans les exemples suivants, nous appliquons chacune des méthodes précédentes à des matrices de différentes tailles pour trouver les déterminants.
Comment trouver le déterminant d'une matrice 2x2
Le déterminant d'une matrice carrée 2x2 est le plus facile à retenir et à calculer. Si l'on désigne une matrice 2x2 A par : 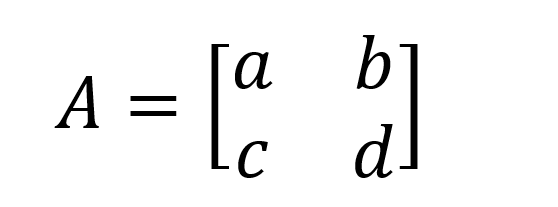
Alors det(A) = (a x d) - (b x c). Par exemple, pour la matrice B ci-dessous :
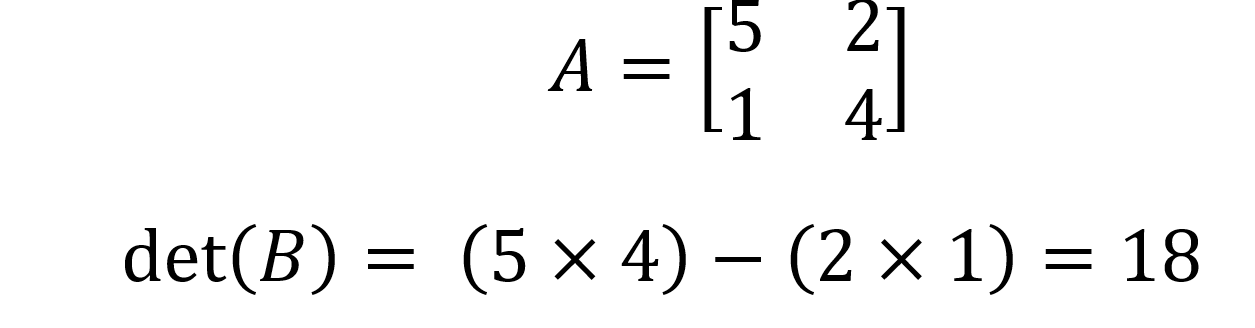
Comment trouver le déterminant d'une matrice 3x3 ?
Bien qu'il existe une formule pour le calcul d'une matrice carrée 3x3, nous démontrons dans cet exemple, pour des raisons pédagogiques, le développement de Laplace (cofacteur). Nous allons calculer le déterminant de la matrice A ci-dessous :
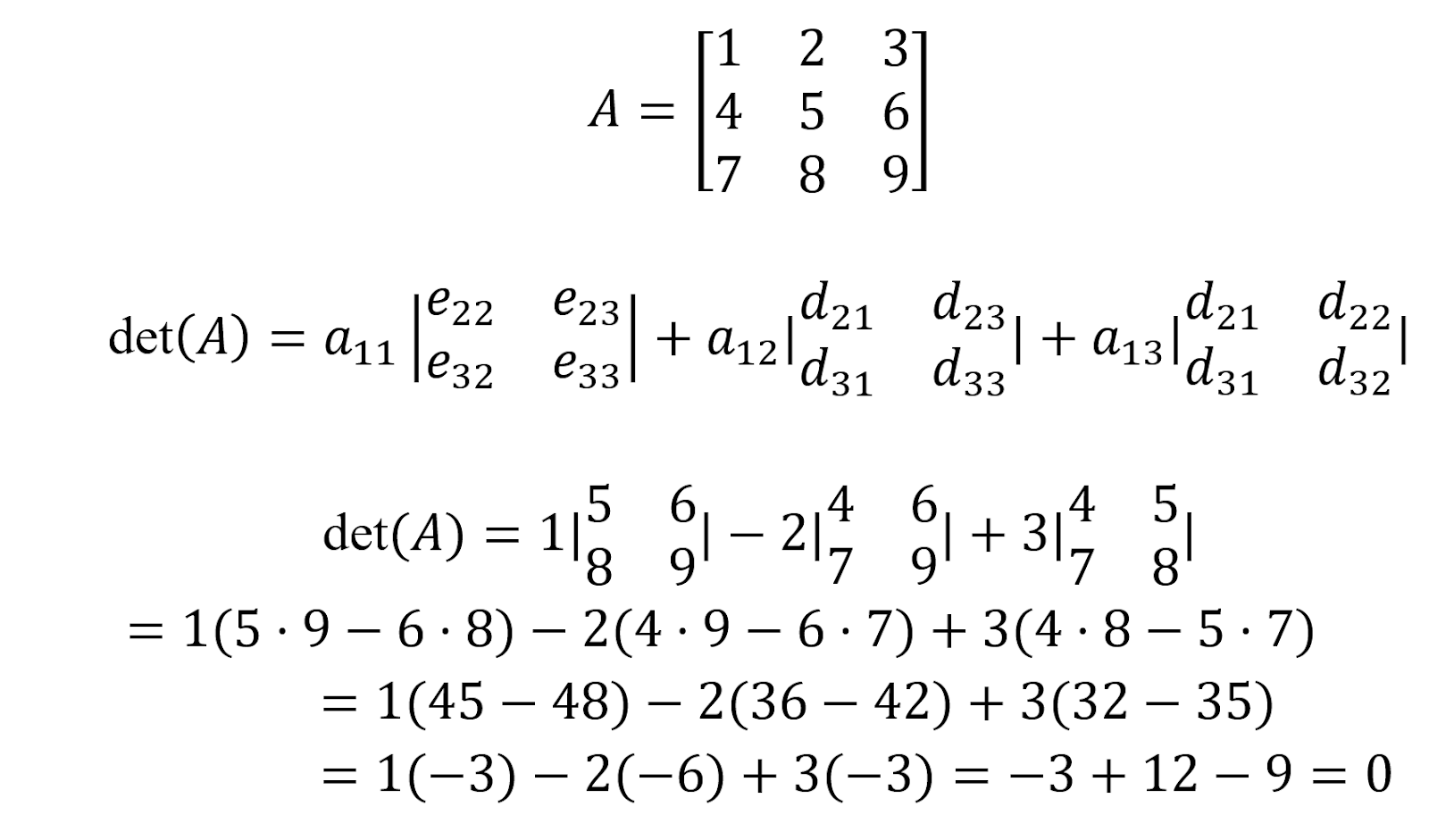
Comment trouver le déterminant d'une matrice 4x4 ?
Nous en profitons maintenant pour montrer la méthode d'élimination gaussienne pour calculer le déterminant d'une matrice 4 x 4 A ci-dessous :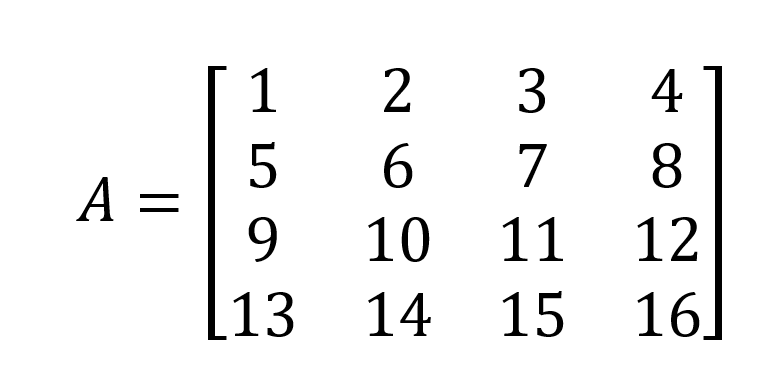
Nous allons transformer cette matrice en une matrice triangulaire supérieure en effectuant des opérations sur les lignes.
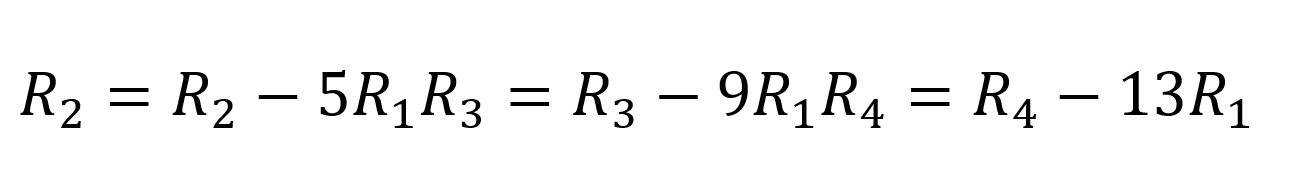
Nous obtenons,
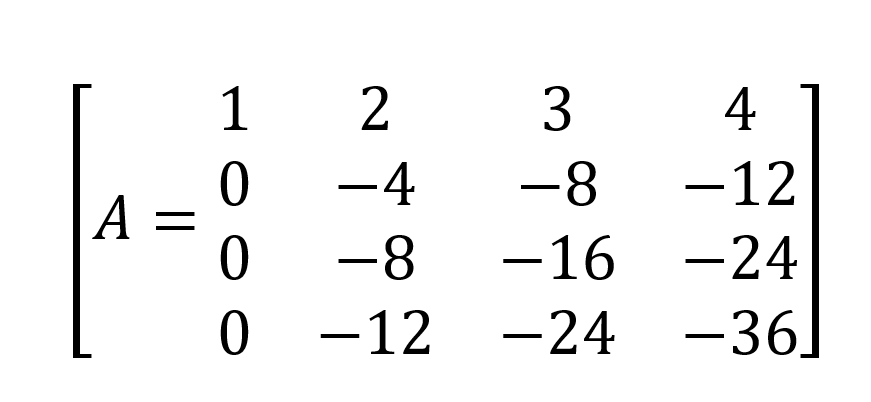
Encore une opération sur les rangs :
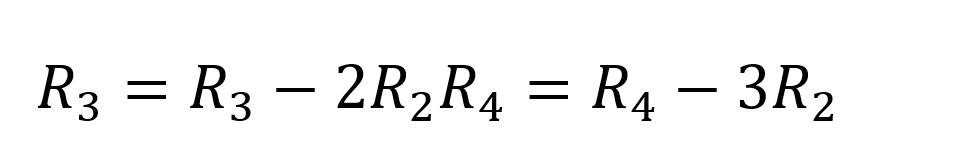
Nous obtenons,
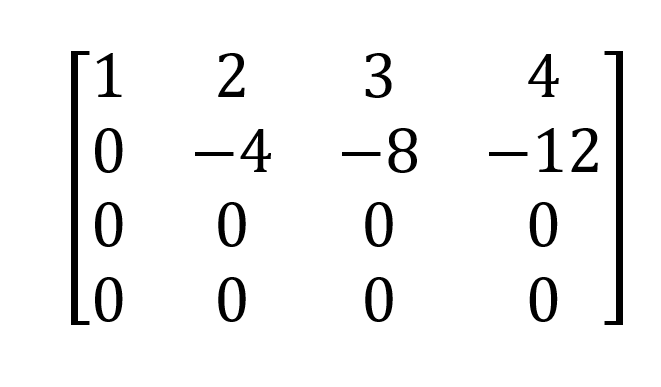
Le déterminant est le produit des éléments diagonaux :
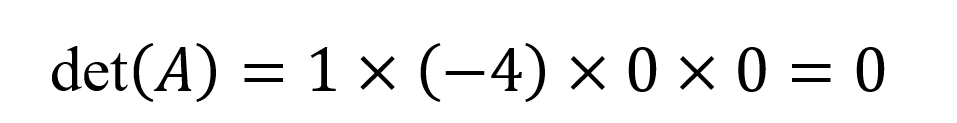
Signification géométrique et algébrique
Comme nous l'avons défini ci-dessus, un déterminant est une fonction qui fait correspondre une matrice carrée à un nombre réel.
En géométrie, un carré est constitué de deux côtés dont le produit est la surface. Et s'il y a trois côtés, on obtient le volume. La (valeur absolue du) déterminant d'une matrice 2 x 2 peut être interprétée comme la surface d'un parallélogramme formé par les deux colonnes de la matrice (en tant que vecteurs directionnels), et le déterminant signé d'une matrice 3 x 3 peut être interprété comme le volume d'un parallélépipède (solide tridimensionnel).
Dans les transformations graphiques, telles que l'étirement ou le rétrécissement d'une image, le déterminant de l'image transformée indique si la surface de l'image originale (matrice) a changé ou non (principe de Cavalieri) après la transformation, tandis que les valeurs propres indiquent si l'image s'est étendue ou rétrécie avec ou sans changement de surface.
Les déterminants peuvent également indiquer si les colonnes ou les lignes d'une matrice sont des combinaisons linéaires les unes des autres (redondance) ou si elles sont linéairement indépendantes, chacune avec une information unique. Si le déterminant d'une matrice n'est pas nul, on en conclut que les colonnes ou les lignes de la matrice sont linéairement indépendantes. Si le déterminant est nul, cela signifie que les colonnes (ou les lignes) de la matrice sont linéairement dépendantes.
Enfin, les déterminants sont également utilisés pour formuler le polynôme caractéristique permettant de calculer les valeurs propres.
Le déterminant en Python et R
Bien que le calcul des déterminants à la main soit une expérience d'apprentissage précieuse pour aiguiser nos compétences mathématiques et développer la sophistication mathématique, un jour ou l'autre, des contraintes de temps et d'énergie peuvent nous obliger à utiliser une calculatrice ou un langage de programmation, tel que Python ou R. Python et R fournissent tous deux des bibliothèques, des fonctions ou des méthodes permettant de calculer le déterminant d'une matrice. Dans les extraits de code suivants, nous démontrons comment calculer le déterminant d'une matrice à l'aide de Python et de R.
Exemple en Python
Deux packages Python populaires pour calculer le déterminant d'une matrice sont Numpy et Sympy (Symbolic Python). Dans l'extrait de code suivant, nous montrons comment calculer le déterminant en utilisant les bibliothèques Numpy et Sympy en Python.
# Computing determinant using Numpy
import numpy as np
matrix = np.array([[1, 2], [3, 4]])
determinant = np.linalg.det(matrix)
print("Determinant:", determinant)
# Computing determinant using Sympy# Import the necessary library
import sympy as sp
matrix = sp.Matrix([[1, 2], [3, 4]])
determinant = matrix.det()
print("Determinant:", determinant)
Exemple R
Le calcul du déterminant d'une matrice dans R ne nécessite pas le chargement d'une bibliothèque. La base R fournit une fonction intégrée pour calculer le déterminant d'une matrice, comme le montre l'extrait de code R suivant :
matrix <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
determinant <- det(matrix)
print(paste("Determinant:", determinant))Applications des déterminants
Systèmes linéaires
Les déterminants peuvent être directement utilisés pour résoudre un système d'équations linéaires à l'aide de la règle de Cramer. Par la règle de Cramer, nous construisons d'abord une matrice composée des coefficients des inconnues du système d'équations et nous calculons son déterminant. Ensuite, nous formons une matrice pour chaque inconnue et calculons son déterminant. Le rapport entre le nouveau déterminant de la matrice et la matrice mère sera la valeur de l'inconnue.
Equations différentielles
Une équation différentielle peut avoir plusieurs solutions (fonctions). Pour s'assurer que les solutions sont linéairement indépendantes (uniques), les déterminants de l'ensemble des solutions de la fonction, appelés Wronskian, sont calculés. Un Wronskien non nul indique que les fonctions / solutions sont linéairement indépendantes dans l'intervalle donné.
Géométrie
En géométrie, le déterminant d'une matrice 2 x 2 peut être interprété comme la surface d'un parallélogramme, et le déterminant d'une matrice 3 x 3 comme le volume d'un solide (parallélépipède). Les déterminants dans la cartographie des fonctions multivariables peuvent aider à comprendre si la cartographie a affecté l'aire ou le volume des fonctions en utilisant le déterminant de la matrice jacobienne.
Points clés à retenir
Les déterminants jouent un rôle plus indirect dans l'apprentissage automatique, les statistiques et le calcul scientifique. Néanmoins, comprendre comment les systèmes d'équations linéaires, l'inversion de matrices, l'infographie et les équations différentielles utilisent les déterminants dans le processus peut mettre en lumière leur signification subtile et la nécessité de comprendre les déterminants. La prochaine fois que vous rencontrerez une erreur de matrice inversible, vous pourrez réfléchir au rôle du déterminant dans la forme et l'indépendance linéaire de la matrice.
Conclusion
J'espère que vous avez pu apprécier l'importance du déterminant pour comprendre le comportement et les transformations des matrices. Notre cours d'algèbre linéaire pour la science des données en R est une excellente étape pour continuer à apprendre les techniques d'algèbre linéaire et les appliquer dans les flux de travail de la science des données.

J'ai suivi une formation en mathématiques et en statistiques. J'ai une grande expérience de la modélisation statistique et des applications d'apprentissage automatique. En outre, j'effectue des recherches sur les mathématiques du ML.