Decomposição de QR para machine learning

A decomposição QR é uma técnica fundamental de fatoração de matriz amplamente usada em vários campos da ciência de dados e do machine learning. Sua capacidade de decompor matrizes complexas em partes mais simples faz com que seja um método muito necessário para resolver problemas de álgebra linear e melhorar a estabilidade dos algoritmos.

Quer você esteja realizando regressão linear por mínimos quadrados ordinários ou criando mecanismos de recomendação em Python ou PySpark, a compreensão da decomposição QR pode aumentar significativamente sua capacidade de trabalhar com grandes conjuntos de dados e modelos matemáticos complexos. 

O que é decomposição QR?

Ao fatorar ou decompor uma matriz, você expressa essa matriz como o produto de duas ou mais matrizes. Em outras palavras, a fatoração de matrizes permite que você decomponha uma matriz em componentes mais simples que, quando multiplicados usando a multiplicação de matrizes, reconstruirão a matriz original. A fatoração de matrizes é importante para nós porque simplifica muitos problemas de álgebra linear, tornando-os mais fáceis de resolver. 

A decomposição QR é um tipo específico de técnica de fatoração de matriz usada para fatorar uma matriz no produto de uma matriz ortogonal Q e uma matriz triangular superior R. A equação que normalmente vemos é A = QR. 

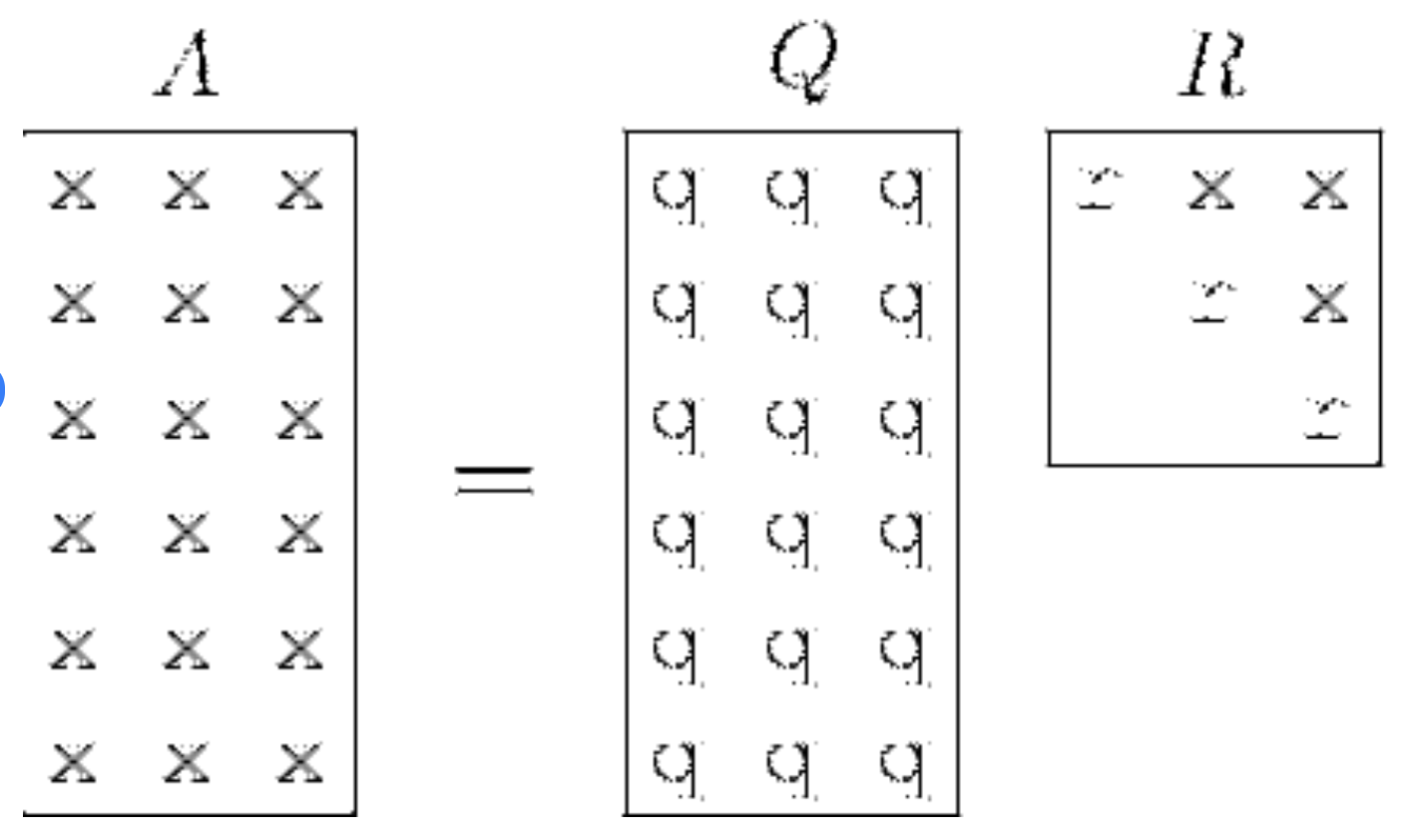
Visualização da decomposição QR. Fonte: ResearchGate

Para entender a decomposição QR, você precisa entender que, na álgebra linear, a multiplicação de matrizes não segue as mesmas regras intuitivas da multiplicação escalar. Para ser mais específico, a multiplicação de matrizes não é comutativa, ou seja, AB ≠ BA em geral e, portanto, a noção de "inverso" é mais complexa.

O que são as matrizes Q e R?

Vamos dar uma olhada nas duas matrizes importantes, Q e R.

Matriz ortogonal Q

Uma matriz ortogonal Q é caracterizada pela propriedade de que sua transposição também é sua inversa, o que é matematicamente representado como ^QTQ= ^QQT = I , em que I é a matriz identidade. Transpor, para fins de contexto, significa virar a matriz sobre sua diagonal.

Uma matriz ortogonal também é caracterizada pelo fato de suas colunas formarem uma base ortonormal. Isso significa duas coisas: Por um lado, as colunas são ortogonais, o que significa que o produto escalar de qualquer par de colunas distintas na matriz é zero. E segundo, cada coluna tem uma magnitude, ou comprimento unitário, de um.

É bom trabalhar com matrizes ortogonais porque elas preservam os comprimentos dos vetores e seus produtos escalares. Portanto, se você tem um vetor e o multiplica por uma matriz ortogonal, o comprimento desse vetor permanece o mesmo. Além disso, se você tiver dois vetores e multiplicar ambos pela mesma matriz ortogonal, o produto escalar entre eles também permanecerá o mesmo. Por fim, como as matrizes ortogonais preservam os comprimentos e os produtos escalares, elas não distorcem as propriedades geométricas dos vetores após nossa transformação. Ou seja, se dois vetores forem perpendiculares antes da transformação, eles permanecerão perpendiculares após a aplicação da matriz ortogonal. 

Matriz triangular superior R

Uma matriz triangular superior R é um tipo de matriz em que todos os elementos abaixo da diagonal principal são zero. Essa forma simplifica as equações de matriz e é particularmente útil na solução de sistemas de equações lineares por meio de substituição posterior ou outro método. Também poderíamos dizer que, na decomposição QR, R representa o componente que captura a magnitude e a orientação da matriz original.

Maneiras de realizar a decomposição QR

Vamos dar uma olhada rápida em algumas das diferentes maneiras de realizar a decomposição QR.

O processo de Gram-Schmidt 

O processo de Gram-Schmidt é um algoritmo usado para converter sistematicamente um conjunto de vetores linearmente independentes em um conjunto ortonormal. Esse processo é usado especificamente para construir a matriz Q em nossa decomposição QR e, depois que tivermos Q, podemos derivar R. 

Rotações Givens

As rotações Givens são outro método para ajudar na decomposição QR. Com as rotações de Givens, uma série de rotações planas é aplicada para introduzir zeros abaixo da diagonal da matriz A. Cada rotação atua em um par de coordenadas, preservando o comprimento do vetor e transformando a matriz em uma forma triangular superior. Esse método é eficiente para matrizes esparsas, pois modifica apenas uma pequena parte da matriz em cada etapa.

Reflexões do proprietário da casa

As reflexões de Householder são uma técnica mais geral que usa matrizes de reflexão, conhecidas como matrizes de Householder, para eliminar sistematicamente os elementos subdiagonais da matriz A. Cada matriz de Householder reflete um vetor em um plano ortogonal ao vetor escolhido para zerar uma coluna abaixo da diagonal. O resultado é uma matriz ortogonal Q e uma matriz triangular superior R. As reflexões de Householder são particularmente boas para matrizes densas devido à sua estabilidade numérica.

Implementação da decomposição QR no R

Nesta seção, praticaremos a decomposição QR no R utilizando a função integrada qr() para uma implementação rápida e, em seguida, percorreremos o processo do zero usando o processo de Gram-Schmidt para desenvolver nossa intuição. Vamos começar criando matrix_A, que usaremos em ambas as seções.  

matrix_A <- matrix(c(21, 21, 22.8, 21.4, 18.7, 18.1, 14.3, 24.4, 22.8, 19.2, 17.8, 16.4, 17.3, 15.2, 10.4, 10.4, 14.7, 32.4, 30.4, 33.9, 21.5, 15.5, 15.2, 13.3, 19.2, 27.3, 26, 30.4, 15.8, 19.7, 15, 21.4, 
              2.62, 2.875, 2.32, 3.215, 3.44, 3.46, 3.57, 3.19, 3.15, 3.44, 3.44, 4.07, 3.73, 3.78, 5.25, 5.424, 5.345, 2.2, 1.615, 1.835, 2.465, 3.52, 3.435, 3.84, 3.845, 1.935, 2.14, 1.513, 3.17, 2.77, 3.57, 2.78, 
              110, 110, 93, 110, 175, 105, 245, 62, 95, 123, 123, 180, 180, 180, 205, 215, 230, 66, 52, 65, 97, 150, 150, 245, 175, 66, 91, 113, 264, 175, 335, 109), 
            nrow = 32, ncol = 3, byrow = FALSE)

# Add column names
colnames(matrix_A) <- c("column_1", "column_2", "column_3")

Decomposição QR usando a função qr()

Podemos fazer essa fatoração em uma única etapa com a função qr(). Atribuímos o resultado a um objeto qr_decomp, que é uma lista que contém a decomposição QR. 

# Perform and Display the QR decomposition
(qr_decomp <- qr(matrix_A))

Quando acessamos o componente de classificação do objeto de decomposição QR, podemos ver o número de colunas linearmente independentes em nossa matriz decomposta. O resultado indica que a matriz tem uma classificação de três, o que significa que há três colunas linearmente independentes, que é o que esperamos. Quando acessamos o componente pivô, podemos ver informações sobre a permutação de colunas usadas durante o processo de decomposição. A saída indica que as colunas da matriz não foram permutadas durante a decomposição, pois os índices de pivô correspondem à ordem original das colunas.

qr_decomp$rank
qr_decomp$pivot

[1] 3
[1] 1 2 3

Como próxima etapa, podemos acessar a matriz Q e a matriz R usando as funções qr.Q() e qr.R(), respectivamente. Podemos ver no resultado que a matriz Q é retangular e a matriz R é quadrada com zeros abaixo da diagonal. 

# Extract and Display the Q and R matrices
(Q_matrix <- qr.Q(qr_decomp))
(R_matrix <- qr.R(qr_decomp))

           [,1]         [,2]         [,3]
 [1,] -0.17721481  0.023462372 -0.015872336
 [2,] -0.17721481 -0.001889138 -0.060272525
 [3,] -0.19240465  0.077625112 -0.019039920
 [4,] -0.18059033 -0.030282834 -0.118470211
 [5,] -0.15780557 -0.089157964  0.064671266
 [6,] -0.15274229 -0.099258795 -0.187022354
 [7,] -0.12067485 -0.161573766  0.277715036
 [8,] -0.20590673  0.012764996 -0.275768785
 [9,] -0.19240465 -0.004891570 -0.156509401
[10,] -0.16202497 -0.082397566 -0.117343880
[11,] -0.15021065 -0.101326680 -0.120852866
[12,] -0.13839633 -0.182888939 -0.033166125
[13,] -0.14599125 -0.136918208  0.028289904
[14,] -0.12826977 -0.170282764  0.014320506
[15,] -0.08776353 -0.381326588 -0.165554550
[16,] -0.08776353 -0.398625266 -0.160607236
[17,] -0.12405037 -0.332631845 -0.083208412
[18,] -0.27341714  0.219354877 -0.069242665
[19,] -0.25653954  0.250472633 -0.021737724
[20,] -0.28607534  0.275923528 -0.005454217
[21,] -0.18143421  0.045632512 -0.033447865
[22,] -0.13080141 -0.140377926 -0.045388530
[23,] -0.12826977 -0.135983661 -0.031340393
[24,] -0.11223605 -0.201937338  0.228196652
[25,] -0.16202497 -0.122661730 -0.004593473
[26,] -0.23037925  0.176744505 -0.035884026
[27,] -0.21940881  0.138786843  0.013273146
[28,] -0.25653954  0.260613237  0.211010230
[29,] -0.13333305 -0.101525496  0.418085457
[30,] -0.16624437 -0.009027316  0.183837006
[31,] -0.12658201 -0.152109209  0.596664759
[32,] -0.18059033  0.012963861 -0.046253102

      column_1  column_2  column_3
[1,] -118.5003 -16.11602 -711.9200
[2,]    0.0000 -10.05857 -496.9319
[3,]    0.0000   0.00000  283.7369

Como etapa final, por curiosidade, podemos verificar qual método a função qr() usa para a decomposição. 

?qr

Você pode ver o seguinte como parte do resultado:  

The function computes the QR decomposition of a matrix using the LINPACK or LAPACK routine dgeqrf.

Se você consultasse a documentação do FORTRAN, veria que dgeqrf é uma rotina do LAPACK que usa as transformações de Householder. 

Decomposição QR do zero

Vamos tentar entender o que está acontecendo com a função qr() recriando não a mesma implementação, mas uma ideia semelhante, seguindo o processo e o raciocínio de Graham-Schmidt. O objetivo deste exercício não é recriar um método exato, mas sim desenvolver nosso entendimento.

Construindo a matriz Q

Para começar a criar nossa matriz Q usando o processo de Graham-Schmidt, precisamos normalizar a primeira coluna dos dados do subconjunto para obter a primeira coluna de Q. O objetivo aqui é transformar nosso conjunto de vetores na matriz A em um novo conjunto de vetores com comprimento unitário de um e garantir que esses vetores sejam ortogonais entre si.

Para encontrar a primeira coluna de Q, extraímos a primeira coluna de A, calculamos a norma euclidiana e, em seguida, realizamos a normalização.

Para revisar, a norma euclidiana é uma medida do comprimento ou da magnitude de um vetor no espaço euclidiano. Consideramos a distância da origem até a extremidade do vetor ao considerar cada elemento do vetor como uma coordenada no espaço multidimensional. Para um vetor v = [v1,v2,...,vn], sua norma euclidiana é calculada da seguinte forma:

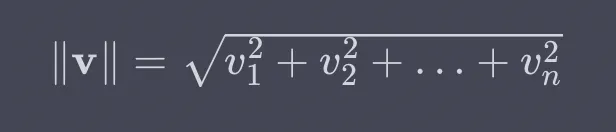
Portanto, para implementar no R, elevamos cada coluna ao quadrado, obtemos a soma, depois a raiz quadrada e, por fim, normalizamos.

# Extract the first column of the subset data
col_1 <- matrix_A[, 1]

# Calculate the Euclidean norm of the first column
norm_col_1 <- sqrt(sum(col_1^2))

# Normalize and display the first column to get the first column of Q
(q1 <- col_1 / norm_col_1)

A segunda coisa que precisamos revisar da álgebra linear é o conceito de projeção. Uma projeção refere-se a uma operação matemática que projeta um vetor em um subespaço. O subespaço pode ser considerado um espaço de dimensão inferior dentro de um espaço vetorial maior. A projeção resultante é um vetor que está dentro do subespaço e é o mais próximo do vetor original que está sendo projetado, que também é ortogonal ao subespaço. 

Vamos tentar visualizar com o gráfico a seguir, em que a projeção p é o ponto mais próximo de a a partir de b, que deve ser perpendicular a b.

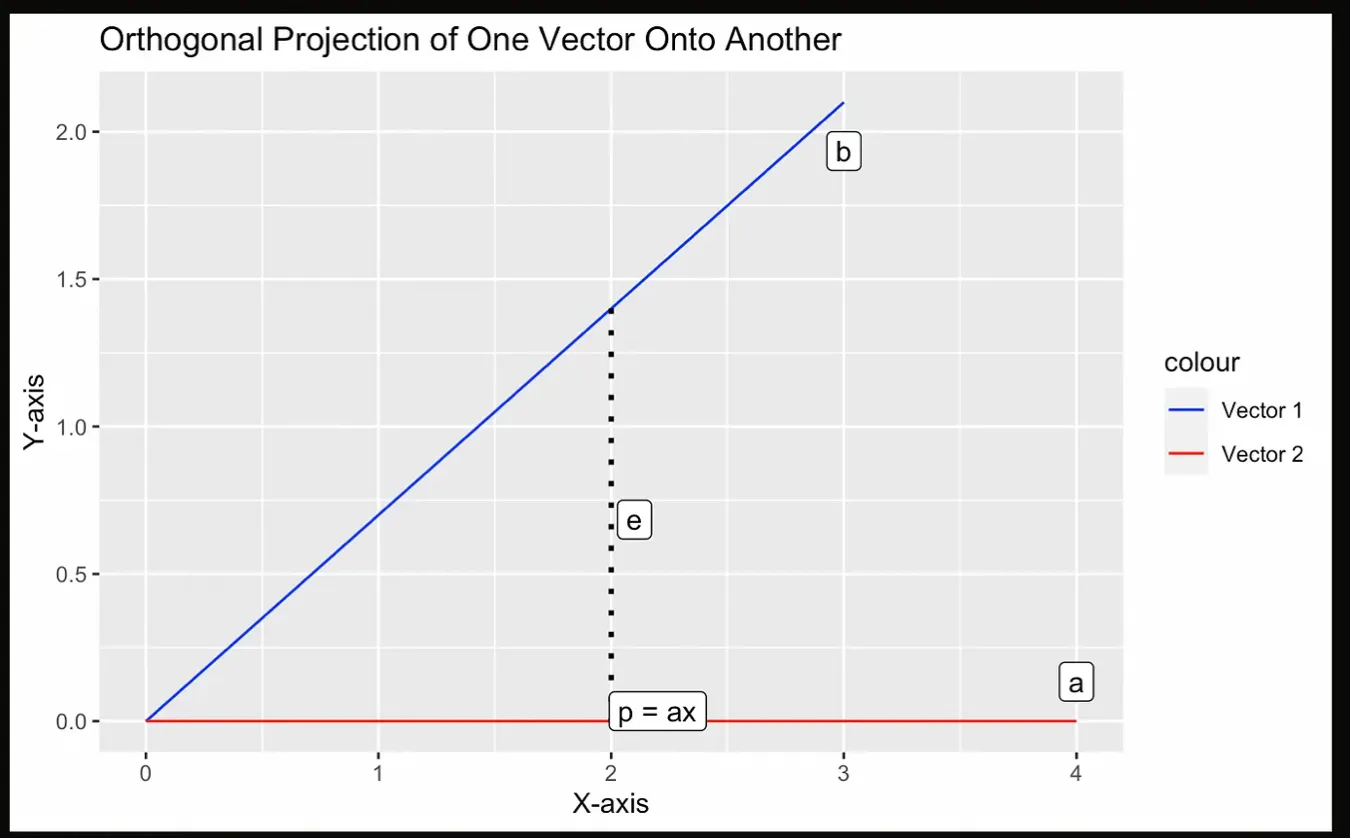
Ilustração de uma projeção. Imagem do autor.

Na próxima etapa da fatoração QR, calculamos o segundo vetor ortogonal calculando primeiro a projeção da segunda coluna de A sobre a primeira coluna de Q e, em seguida, subtraindo esse resultado da segunda coluna de A. O vetor resultante será ortogonal ao primeiro vetor. Como etapa final, normalizamos esse vetor para obter a segunda coluna de Q.

Vamos analisar a equação para uma projeção. A projeção é a matriz que é a vezes a-transposição sobre o valor escalar que é a-transposição vezes a, multiplicado por b.

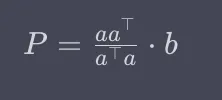
Ou, alternativamente:

Você pode estar se perguntando: Como esses dois métodos são iguais? Bem, quando analisamos a primeira equação acima, a parte à esquerda de b calcula uma matriz que essencialmente captura a direção definida pelo vetor a e o fator de escala para essa direção. Isso é semelhante ao cálculo do vetor unitário de a no método do produto escalar. 

O código R a seguir calcula a projeção do vetor col_2 no vetor q1 usando o método do produto escalar.

# Extract the second column of the subset data
col_2 <- matrix_A[, 2]

# Calculate the projection of col_2 onto q1
projection_col_2_q1 <- sum(col_2 * q1) * q1

# Calculate the second orthogonal vector
v2 <- col_2 - projection_col_2_q1

# Calculate the Euclidean norm of the second orthogonal vector
norm_v2 <- sqrt(sum(v2^2))

# Normalize the second orthogonal vector to get the second column of Q
q2 <- v2 / norm_v2

Como podemos ver no código acima, a construção do segundo vetor ortogonal e da coluna correspondente da matriz Q envolve um processo de projeção, subtração e normalização. As etapas básicas são semelhantes às da criação da primeira coluna de Q, mas são um pouco diferentes e um pouco mais complexas: Primeiro, extraímos a segunda coluna de A; depois, criamos uma projeção no primeiro vetor de Q; em seguida, subtraímos a projeção da segunda coluna de A; depois, realizamos a normalização; por fim, criamos a segunda coluna de Q.

Você pode repetir essa segunda etapa para q3 até a última coluna. No nosso caso, os vetores ortogonais q1, q2, e q3 ​formam a base da matriz ortogonal Q. Esses vetores são essenciais porque fornecem a base para expressar os dados originais em um novo sistema de coordenadas.

Aqui, vemos que o processo de Gram-Schmidt é um processo iterativo que garante que cada vetor sucessivo seja ortogonal aos anteriores. Lembramos também que a ortogonalidade significa que o produto escalar de dois vetores é zero, indicando que eles são perpendiculares entre si no espaço vetorial. Vamos confirmar a ortogonalidade de q1 e q2 usando seu produto escalar:

# Calculate the dot product of q1 and q2
dot_product_q1_q2 <- sum(q1 * q2)

# Print the dot product to confirm orthogonality
print(dot_product_q1_q2)

[1] 2.43295e-16

Construindo a matriz R

Agora que temos nossa matriz Q, precisamos construir a matriz R. A matriz R na decomposição QR contém informações sobre as relações entre as colunas da matriz ortogonal Q e o conjunto de dados original. É uma matriz triangular superior, e cada elemento da parte triangular superior de R é obtido pelo cálculo do produto escalar das colunas correspondentes de Q e dos dados originais.

Para construir a matriz triangular superior R, precisamos calcular os produtos de pontos de cada coluna de Q com cada coluna do conjunto de dados original. Isso resultará em uma matriz que tem o mesmo número de linhas que o número de colunas em Q, e será triangular superior devido ao nosso processo anterior.

matrix_A <- matrix_A %>% as.matrix()

# Calculate and display the R matrix by multiplying Q^T and the subset data
R_matrix <- t(Q_matrix) %*% matrix_A

Vemos que a saída da nossa matriz R parece um pouco diferente desta vez. O motivo é que a função qr() usa reflexões de Householder com mais estabilidade numérica do que o processo inspirado em Graham-Schmidt que nós mesmos criamos.

         column_1      column_2  column_3
[1,] -1.185003e+02 -1.611602e+01 -711.9200
[2,]  5.814446e-16 -1.005857e+01 -496.9319
[3,]  7.633287e-15  1.338669e-15  283.7369

Podemos verificar a reconstrução multiplicando Q e R e vendo que você obtém matrix_A. Aqui, %*% é para multiplicação de matriz em R.  

Q_matrix %*% R_matrix

   column_1 column_2 column_3
 [1,]     21.0    2.620      110
 [2,]     21.0    2.875      110
 [3,]     22.8    2.320       93
 [4,]     21.4    3.215      110
 [5,]     18.7    3.440      175
 [6,]     18.1    3.460      105
 [7,]     14.3    3.570      245
 [8,]     24.4    3.190       62
 [9,]     22.8    3.150       95
[10,]     19.2    3.440      123
[11,]     17.8    3.440      123
[12,]     16.4    4.070      180
[13,]     17.3    3.730      180
[14,]     15.2    3.780      180
[15,]     10.4    5.250      205
[16,]     10.4    5.424      215
[17,]     14.7    5.345      230
[18,]     32.4    2.200       66
[19,]     30.4    1.615       52
[20,]     33.9    1.835       65
[21,]     21.5    2.465       97
[22,]     15.5    3.520      150
[23,]     15.2    3.435      150
[24,]     13.3    3.840      245
[25,]     19.2    3.845      175
[26,]     27.3    1.935       66
[27,]     26.0    2.140       91
[28,]     30.4    1.513      113
[29,]     15.8    3.170      264
[30,]     19.7    2.770      175
[31,]     15.0    3.570      335
[32,]     21.4    2.780      109