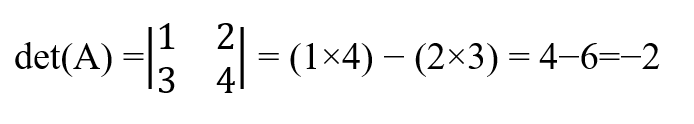The Determinant: How It Works and What It Tells Us

Information and data stored on a computing architecture are in the form of matrices. Therefore, underneath most scientific, machine learning, and computations lie matrices of different dimensions.

Matrices are fundamental mathematical objects in linear algebra. Matrices themselves have some properties, such as dimension, sparsity, eigenvalues, and determinants.

A determinant is a fundamental property of a square matrix that plays significant direct and indirect roles in matrix operations, such as invertibility, solving linear systems in engineering, and transformations in geometry and computer graphics.

In this article, you will learn about the determinants of a square matrix, their applications, and some methods to calculate them by hand and with Python and R programs.

What Is a Determinant?

A determinant is a function that maps a square matrix onto a real scalar (single value). In mathematics, the determinant of a square matrix A is shown as det(A) or |A|.

Like mathematics itself, the determinant has a long history dating back to Chinese mathematicians. In ancient China, mathematicians used determinants to solve systems of linear equations (their method of solving linear equations is now called Cramer’s Rule). Later in 16th century Europe, mathematician Cardano brought determinants to the fore by applying them in the solution of systems of linear equations. Later, Takakazu (17th century), Leibniz (17th century), Vandermonde , and Cauchy (18th century) established the theoretical foundation of determinants in pure mathematics.

Properties of Determinants

Although determinants need to be computed for each square matrix, they have some known properties in general and for some specific matrices. In addition, determinants subject to certain mathematical operations show some patterns and properties as well. Some of the well-known properties of determinants are as follows:

The determinant of a square identity matrix is 1

An identity matrix has values of 1 on the diagonal and 0 elsewhere.

Swapping two rows or columns will change the sign of the determinant

For example, in the following matrix, the determinant is:

If we swap the rows, the result has a sign change.

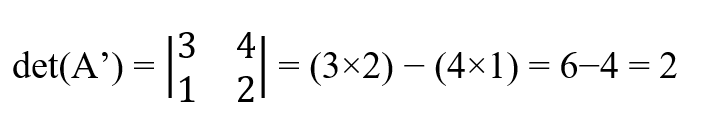
The determinant of triangular matrices equals the product of the diagonal elements

If a matrix is lower or upper triangular, then to compute the determinant, we only need to multiply the diagonal values together. For example, in the following upper triangular square matrix, the determinant is calculated by multiplying the diagonal values:

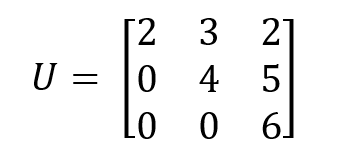
We simply multiply the diagonal elements to compute the determinant: det(U)=2×4×6=48

The determinant is invariant under matrix similarity

Two matrices are similar if they are derived from one linear transformation and have different bases. If two matrices are similar, then they have the same determinant (and eigenvalues, traces, and characteristic polynomials).

The determinant of a matrix product is the product of the matrices' determinants.

As an example, the individual determinants of matrices A and B are shown here:

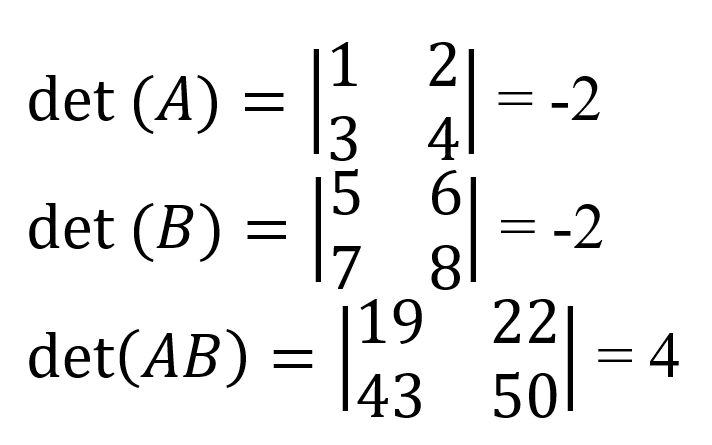
Determinants are invariant under transposition

For example, the determinant of matrix A and AT is the same (-9).

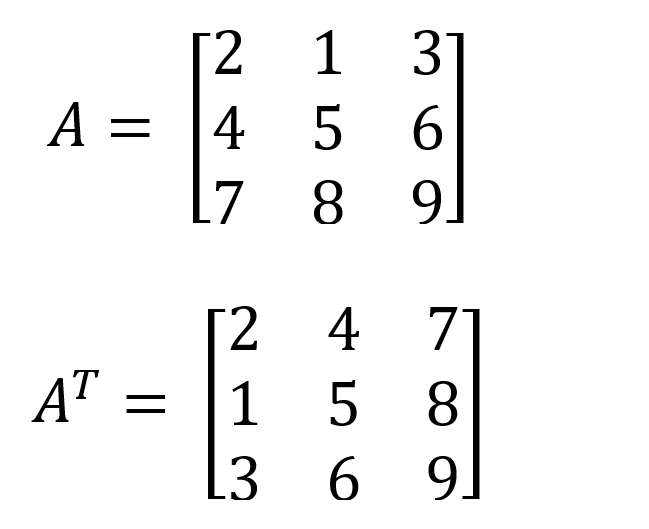
Methods to Calculate Determinants

There are different methods to calculate the determinant of a square matrix, such as the Leibniz formula, Laplace expansion, and Gaussian elimination. The choice of the method is subject to the size of the matrix and computational costs. We describe some of these methods below:

Leibniz formula

Leibniz formula for finding the determinant of a square matrix is best suitable for small matrices, especially if computation is conducted totally or in part by hand. Leibniz formula for finding the determinant of a matrix is as follows:

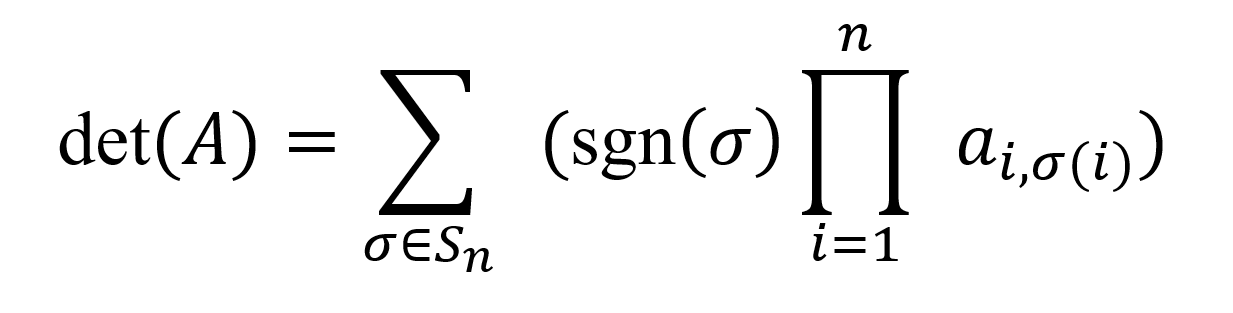
Where Sn denotes the set of all permutations of the numbers 1,2,…,n and sgn(σ)is the sign of the permutation, which is +1 if the permutation is even and −1 if the permutation is odd. The term ai,σ is an element of the matrix A.

Laplace expansion

Laplace expansion is ideal for larger matrices. In Laplace or cofactor expansion, a large matrix is divided into smaller matrices. Then, a scheme involving the determinant (minor) of a smaller matrix and its cofactor is designed and iterated across rows or columns.

Gaussian elimination

Because the determinant of a triangular matrix is the product of its diagonal elements, reducing a matrix to a diagonal matrix makes the calculation of the determinant more efficient. In Gaussian elimination, a series of row operations are performed to reduce the full matrix to the row echelon or upper triangular form. Then, the determinant is calculated by multiplying the diagonal elements.

How to Find the Determinant for Different Size Matrices

In the following examples, we apply each of the foregoing methods to matrices of different sizes to find the determinants.

How to find the determinant for a 2x2 matrix

The determinant of a 2x2 square matrix is the easiest to remember and calculate. If we denote a 2x2 matrix A as: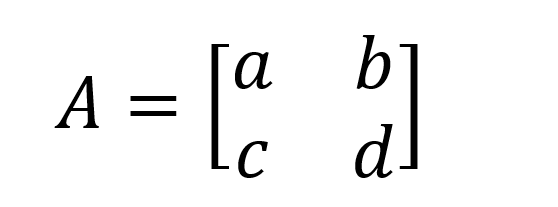 

Then det(A) = (a x d) - (b x c). For example, for matrix B below:

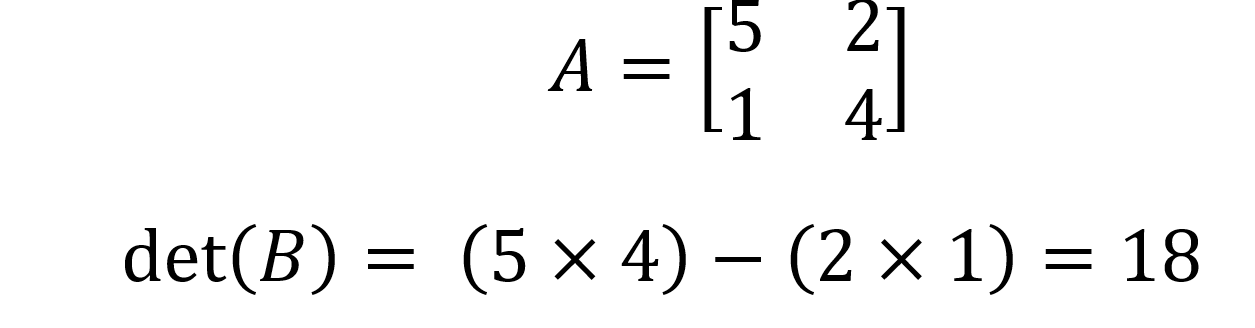
How to find the determinant for a 3x3 matrix

Although there is a formula for the calculation of a 3x3 square matrix, for pedagogical reasons we demonstrate the Laplace (co-factor) expansion in this example. We will calculate the determinant of matrix A below:

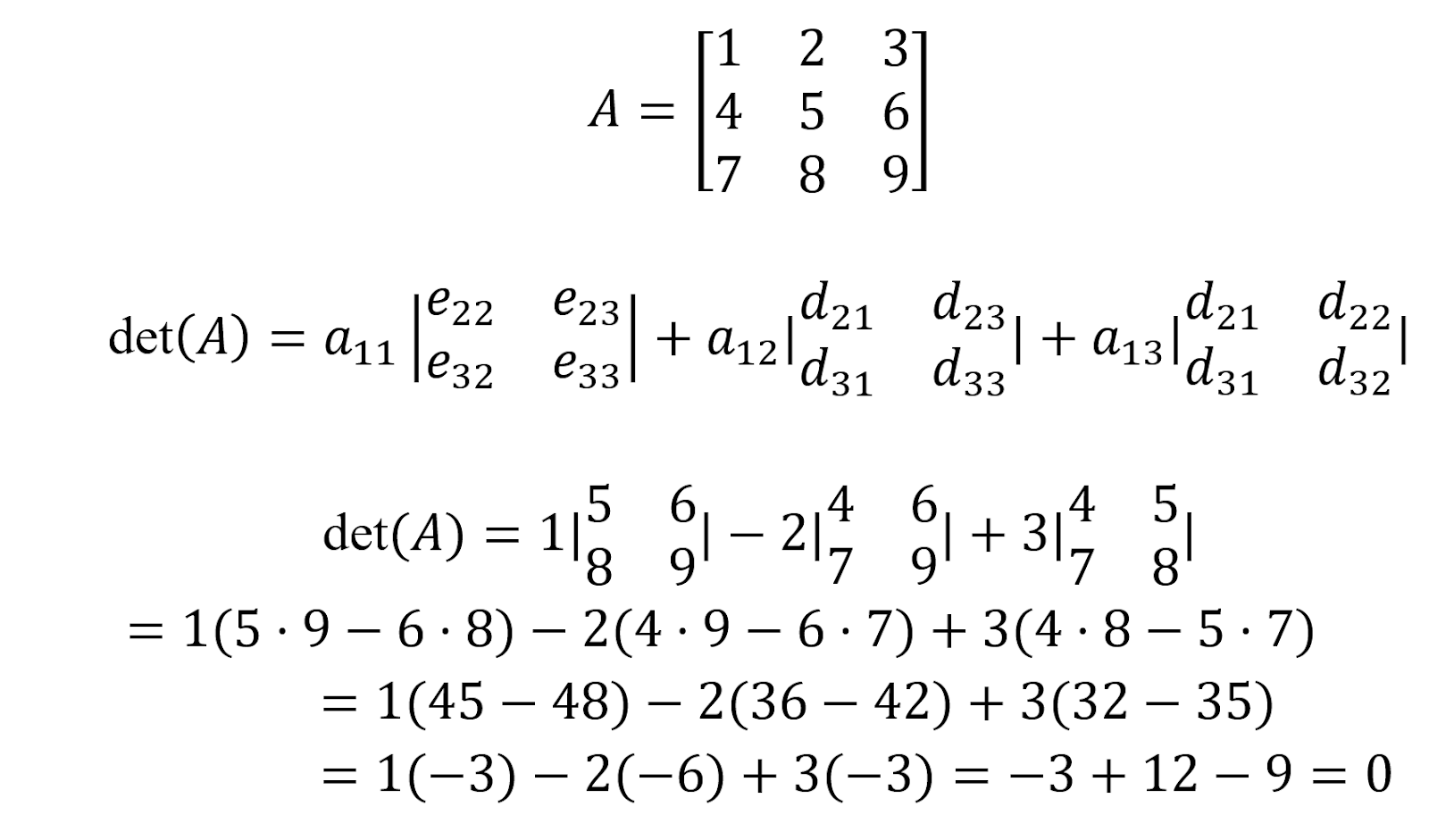
How to find the determinant for a 4x4 matrix

We now use the opportunity to show the Gaussian elimination method to calculate the determinant of a 4 x 4 matrix A below: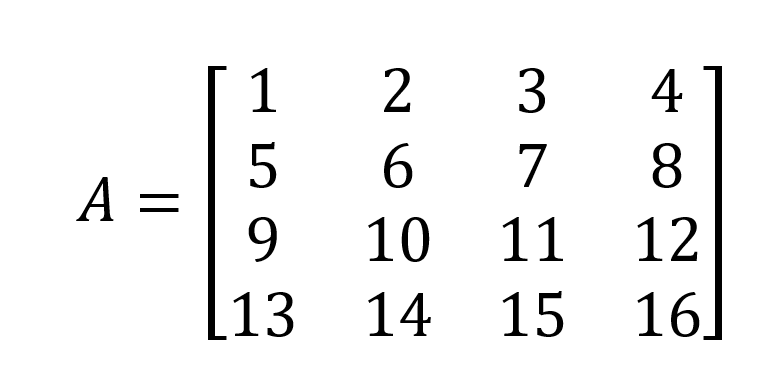

We will transform this matrix into an upper triangular matrix by performing row operations.

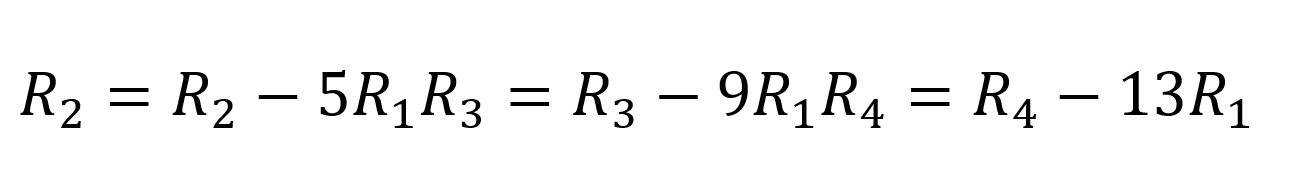
We get,

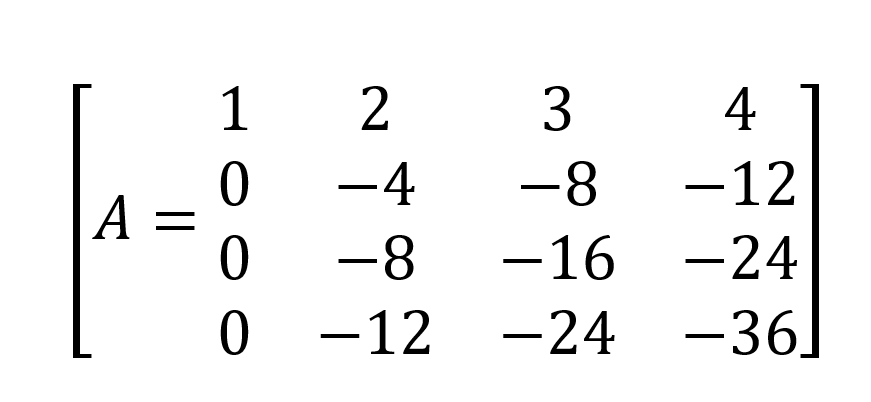
One more row operation:

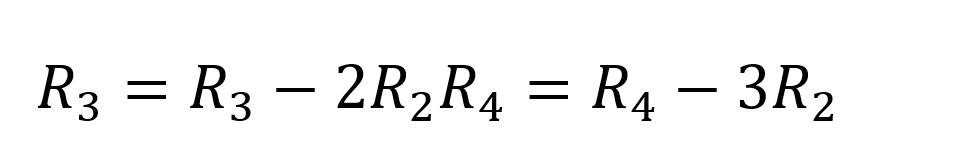
We get, 

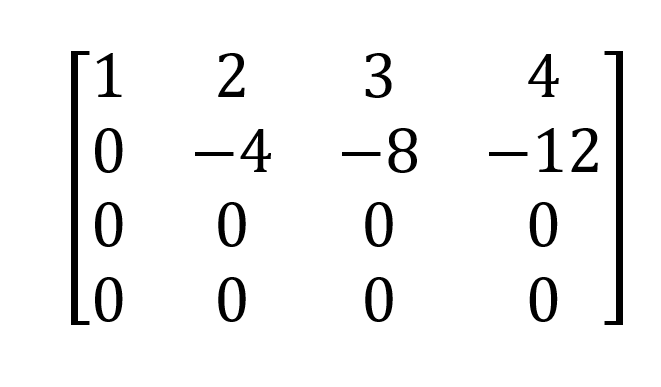
And the determinant is the product of the diagonal elements:

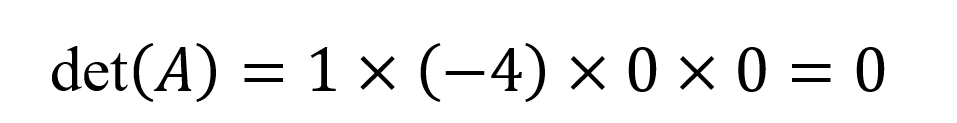
Geometric and Algebraic Significance

As we defined above, a determinant is a function that maps a square matrix to a real number.

In geometry, a square consists of two sides, the product of which is the surface area. And if there are three sides, we get the volume. The (absolute value of) the determinant of a 2 x 2 matrix can be interpreted as the area of a parallelogram formed by the two columns of the matrix (as directional vectors), and the signed determinant of a 3 x 3 matrix can be interpreted as the volume of a parallelepiped (three-dimensional solid).

In graphical transformations, such as stretching or shrinking an image, the determinant of the transformed image shows if the area of the original image (matrix) has changed or not (Cavalieri’s principle) after transformation, while the eigenvalues show if the image has extended or shrunk with or without changing the area.

Determinants can also indicate if columns or rows of a matrix are linear combination of each other (redundancy) or they are linearly independent each with unique information. If the determinant of a matrix is non-zero, we conclude that the columns or rows of the matrix are linearly independent. If the determinant is zero, it shows that the columns (or rows) of the matrix are linearly dependent.

Finally, determinants are also used in formulating the characteristic polynomial for computing the eigenvalues.

The Determinant in Python and R

Although calculating determinants by hand is a valuable learning experience for sharpening our mathematical skills and developing mathematical sophistication, eventually time and energy constraints may have us use a calculator or a programming language, such as Python or R. Both Python and R provide libraries, functions, or methods to calculate the determinant of a matrix. In the following code snippets, we demonstrate how to calculate the determinant of a matrix using Python and R.

Python example

Two popular Python packages for computing the determinant of a matrix include Numpy and Sympy (Symbolic Python). In the following code snippet, we show how to compute the determinant using Numpy and Sympy libraries in Python.

# Computing determinant using Numpy
import numpy as np
matrix = np.array([[1, 2], [3, 4]])
determinant = np.linalg.det(matrix)
print("Determinant:", determinant)
 
# Computing determinant using Sympy# Import the necessary library
import sympy as sp
matrix = sp.Matrix([[1, 2], [3, 4]])
determinant = matrix.det()
print("Determinant:", determinant)
 

R example

Computing the determinant of a matrix in R does not require loading a library. The base R provides a built-in function to compute the determinant of a matrix, as shown in the following R code snippet:

matrix <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
determinant <- det(matrix)
print(paste("Determinant:", determinant))

Applications of Determinants

Linear systems

Determinants can be directly used in solving a system of linear equations using Cramer’s Rule. By Cramer’s rule, first we construct a matrix consisting of the coefficients of the unknowns in the system of equations and compute its determinant. Next, we form a matrix for each unknown and compute its determinant. The ratio of the new matrix determinant to the parent matrix will be the value of the unknown.

Differential equations

A differential equation may have several solutions (functions). To make sure the solutions are linearly independent (unique), the determinants of the set of function solutions, called the Wronskian, are computed. A non-zero Wronskian indicates that the functions / solutions are linearly independent in the given interval.

Geometry

In geometry, the determinant of a 2 x 2 matrix can be interpreted as the area of a parallelogram, and the determinant of a 3 x 3 matrix can be interpreted as the volume of a solid (parallelepiped).  Determinants in multivariable function mapping can help use understand if the mapping has affected the area or the volume of the functions using the determinant of the Jacobian matrix.

Key Points to Remember

Determinants play a more indirect role in machine learning, statistics, and scientific computing. Nevertheless, understanding how system of linear equations, matrix inversion, computer graphics, and differential equations use determinants in the process can shed light on their subtle significance and the need to understand determinants. Next time you encounter an invertible matrix error, you might think about the role of determinant in the shape and linear independence of the matrix.

Conclusion

I hope you have come to appreciate how the determinant is important in understanding matrix behavior and transformations. Our Linear Algebra for Data Science in R course is a great next step to keep learning linear algebra techniques and apply the techniques in data science workflows.