Equação característica: Tudo o que você precisa saber sobre ciência de dados

Com o crescimento exponencial da disponibilidade de dados e técnicas de aprendizado de máquina, a álgebra linear encontrou um lugar fundamental na matemática do aprendizado de máquina e da ciência de dados. Assim, os aspirantes a cientistas de dados e de aprendizado de máquina se beneficiarão muito com o aprendizado de conceitos fundamentais de álgebra linear, incluindo vetores e matrizes, suas propriedades e operações comuns aplicadas a eles.

Incentivo você a fazer o curso Álgebra linear para ciência de dados em R para desenvolver uma base matemática sólida para ciência de dados e aprendizado de máquina. Ao fazer o curso, você passará a apreciar a álgebra linear como uma disciplina bonita e interessante que envolve a síntese da álgebra e da geometria (por meio de linhas, planos e volumes). Em particular, você verá como os dados de alta dimensão são adequados para serem representados na forma de objetos vetoriais (por exemplo, texto, imagens, áudio e recursos) e verá como esses objetos matemáticos como vetores têm amplas aplicações em ciência e engenharia, como física, estatística e ciência da computação.

Neste artigo, examinaremos de perto um dos objetos fundamentais da álgebra linear chamado matriz. Como outros objetos matemáticos, as matrizes têm alguns atributos que as caracterizam. Em particular, em , analisarei e apresentarei um atributo característico de uma matriz quadrada: o polinômio característico ou equação característica. Vamos dar uma olhada.

Definição da equação característica

Um polinômio é uma função com incógnitas de potência n. O desconhecido é geralmente indicado pela letra x, mas em casos especiais, uma notação diferente é usada, como a letra grega 𝝀 (lambda), que usaremos em nossa notação. O polinômio característico de uma matriz quadrada A ∈Rn× n e a incógnita 𝝀 são definidos como:

Onde det(.) é o determinante de uma matriz quadrada e I é a matriz identidade.

Quando definimos esse polinômio característico igual a zero (para resolver para 𝝀), chamamos isso de equação característica. As raízes dessa equação polinomial são chamadas de valores próprios, que são conceitos importantes na transformação de matrizes e no aprendizado de máquina (por exemplo, redução de dimensionalidade). Se você não tiver certeza sobre vetores e valores próprios, temos um tutorial sobre o assunto: Vetores e valores próprios: Principais percepções para a ciência de dados.

Derivação e cálculo da equação característica

Mostramos como um polinômio característico é formulado para uma matriz quadrada 2x2 quadrada A, onde:

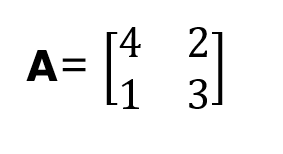
A partir da definição de um polinômio característico, temos:

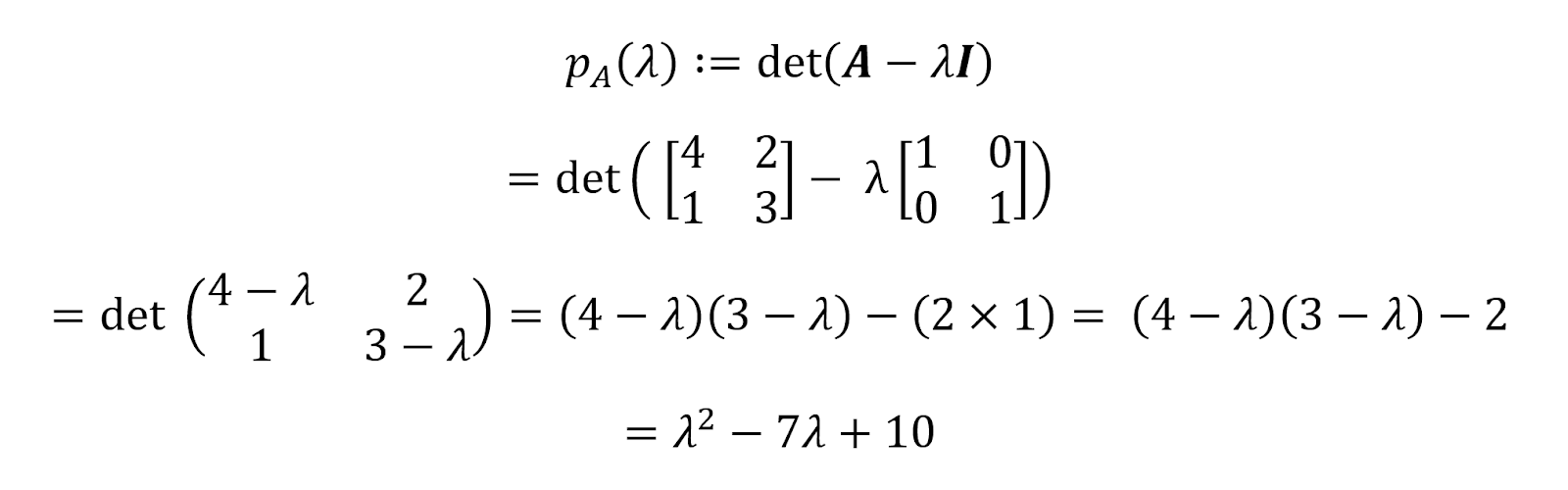
Portanto, o polinômio característico da matriz A acima é p_A(𝝀)=𝝀2-7𝝀+10. Podemos encontrar as raízes desse polinômio igualando-o a zero.

Usando a equação característica para encontrar valores e vetores próprios

Um polinômio característico de uma matriz quadrada contém características importantes sobre sua matriz associada, incluindo os valores próprios e o determinante. Portanto, é possível extrair os valores próprios de um polinômio característico resolvendo a questão do desconhecido. Ilustramos acima o processo de encontrar valores próprios do polinômio característico de uma matriz quadrada A 2x2. Como mostramos, o polinômio característico dessa matriz é:

Agora, para encontrar o(s) valor(es) próprio(s), igualamos esse polinômio a zero e encontramos as raízes usando métodos algébricos (ou computacionais):

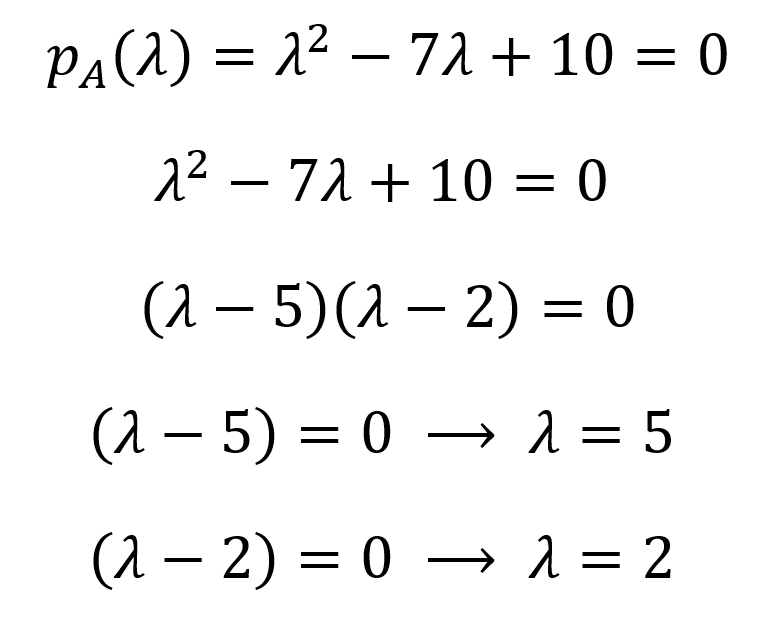
Portanto, os valores próprios são 𝝀₁=5 e 𝝀₂=2 (os valores próprios são convencionalmente listados em ordem decrescente, pois implicam a quantidade de informações em determinadas matrizes de dados). O conjunto de todos os valores próprios de uma matriz é chamado de espectro próprio ou espectro dessa matriz. A partir dos valores próprios, podemos derivar os vetores próprios de uma matriz no espaço nulo usando (A-𝝀I)x=0 para cada valor próprio:

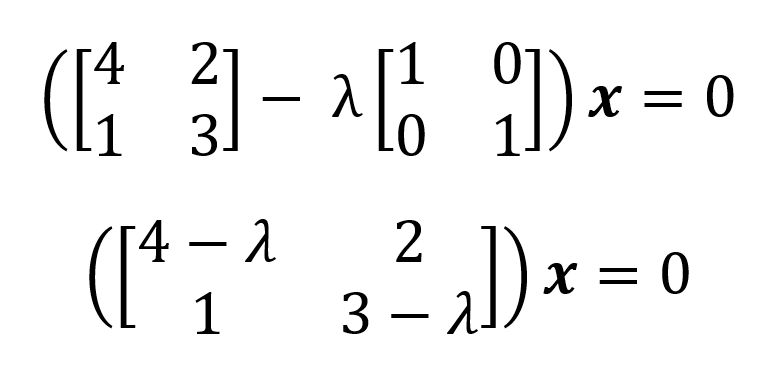
Para𝝀₁=5 inserimos 5 e resolvemos o sistema homogêneo de equações:

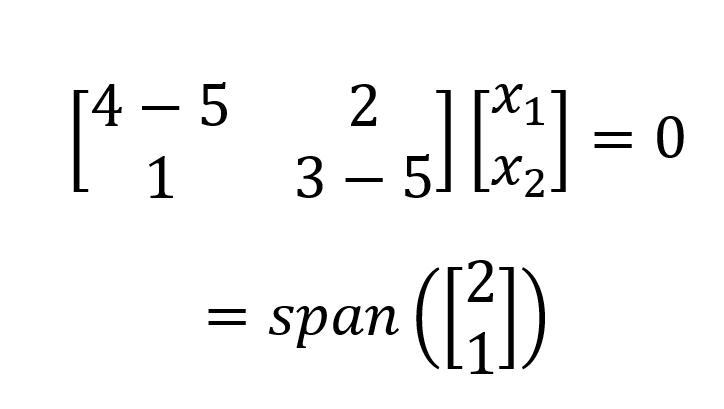
O que resulta em um eigenspace unidimensional (ou seja, um vetor de base). Realizamos o mesmo processo para 𝝀₂=2 e obtemos:

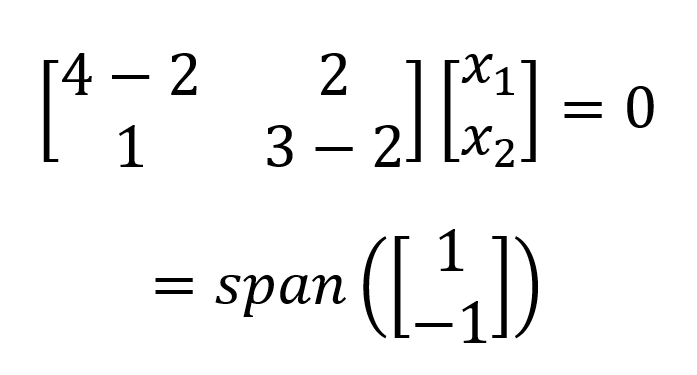
Neste exemplo, temos dois valores próprios distintos. Uma matriz também pode ter vários valores próprios idênticos repetidos, o que resulta em um espaço próprio multidimensional (ou seja, vários vetores de base). Nesse caso, a dimensionalidade do espaço eletrônico abrangido por vetores próprios distintos é chamada de multiplicidade geométrica do valor próprio i.

Por outro lado, o número de vezes que um valor próprio de uma matriz é repetido é chamado de multiplicidade algébrica. Provavelmente, uma das aplicações mais interessantes de autovalores e autovetores é o algoritmo PageRank que o Google usa para classificar a importância dos resultados de pesquisa. Se você estiver interessado, nosso curso Predictive Analytics using Networked Data in R tem um capítulo interessante sobre o algoritmo PageRank. 

Técnicas computacionais

Um polinômio característico é, na verdade, um polinômio matemático com propriedades especiais (por exemplo, inclui o traço, o determinante e os valores próprios de uma matriz quadrada). Dessa forma, encontrar as raízes da equação característica se torna complicado com graus mais altos de n. 

Além disso, a derivação do polinômio característico exige que você calcule o determinante da matriz quadrada. Embora, por motivos pedagógicos, tenhamos fornecido um exemplo e um método para derivar e resolver o polinômio característico no papel e à mão, em aplicativos reais de ciência de dados, métodos numéricos (computacionais) são usados para calcular ou aproximar as raízes de um polinômio característico. A expansão de Laplace, a eliminação Gaussiana e as decomposições QR são alguns métodos que podem encontrar numericamente os determinantes. 

Para encontrar as raízes do polinômio característico, os algoritmos comuns incluem o método de Newton-Raphson, a bissecção, o método secante e o método de Muller.

Aplicações da equação característica

Os valores e vetores próprios são características matemáticas fundamentais das matrizes que podem ser derivadas de uma equação característica de uma matriz quadrada. Na estatística e no aprendizado de máquina, as equações características são usadas para diferentes algoritmos que se baseiam em valores próprios e que são usados para redução de dados e algoritmos de extração de informações, como:

• Análise de componentes principais (PCA) e redução de dimensionalidade, em que um conjunto de dados é reduzido a um número menor de vetores com base nos valores dos autovalores extraídos.
• Agrupamento espectralque é uma técnica baseada no espectro de eigens da matriz de similaridade de um conjunto de dados para reduzir a dimensionalidade dos dados como uma etapa antes de executar algoritmos de agrupamento, como o agrupamento k-means.
• Teoria dos gráficos e análise de rede, em que os valores e vetores próprios são usados para particionar um gráfico em comunidades (componentes principais), incorporando o gráfico em um espaço de dimensão inferior para visualização e esparsificação espectral para aproximar um gráfico com espectro próprio semelhante.
• Séries temporaisA análise de espectro singular é usada para descobrir padrões subjacentes na série, como tendências, ciclos e anomalias.

Propriedades do polinômio característico

Como objeto matemático, um polinômio característico tem algumas propriedades interessantes, inclusive:

• Monic: O coeficiente principal de um polinômio característico é sempre um (mônico).
• Grau: O grau n de um polinômio característico é sempre igual ao tamanho damatriz nx n associada.
• Invariância sob similaridade de matriz: Se transformarmos uma matriz e o resultado for uma matriz semelhante, ambas terão um polinômio característico idêntico (ou seja, a matriz semelhante transformada mantém o polinômio característico original).
• Coeficientes: O primeiro termo principal do polinômio característico é o determinante da matriz associada, e o penúltimo coeficiente é o traço sem sinal da matriz associada c₀=det(A) e c_n-1=-1^n-1tr(A)
• No polinômio característico, se substituirmos cada incógnita pela matriz quadrada original, o resultado será uma matriz zero (Teorema de Cayley-Hamilton). Em outras palavras, o polinômio característico é um polinômio aniquilador para a matriz quadrada. Nessa forma, os valores próprios podem ser derivados diretamente da matriz quadrada. Dessa forma, pode-se afirmar que toda matriz quadrada satisfaz sua própria equação característica.

Tópicos avançados

Por fim, quero oferecer alguns detalhes mais avançados relacionados aos polinômios característicos e às propriedades da matriz como uma visão mais aprofundada da matemática, mas sem muitos detalhes.

• Polinômio mínimo: Um polinômio mônico intimamente relacionado ao polinômio característico é o polinômio mínimo, que é um polinômio de grau mínimo positivo que aniquila a matriz quadrada A. Como um polinômio característico também pode aniquilar sua matriz quadrada, o polinômio mínimo pode ser derivado desse polinômio característico.
• Similaridade e diagonalização: Duas matrizes são semelhantes se estiverem relacionadas entre si por meio de uma transformação linear comum. Se duas matrizes forem semelhantes, elas também terão a mesma classificação, traço, determinante, valores próprios, polinômio característico e polinômios mínimos. 
• Equação característica de potências e funções de matriz: Em uma potência de matriz, os valores próprios são elevados à kª potência da matriz^Ak e o polinômio característico correspondente é derivado como det(A^k-λI). Para uma função de matriz f(x), o polinômio característico pode ser derivado avaliando-se f() nos valores próprios de A.

Conclusão

Neste artigo, aprendemos sobre o polinômio característico e como ele contém propriedades importantes de uma matriz quadrada, como os valores próprios, o traço e o determinante. Dada a importante função dos valores próprios na ciência de dados e no aprendizado de máquina, a compreensão da equação característica nos ajuda muito a entender como o aprendizado de máquina e os algoritmos estatísticos extraem os principais componentes de uma matriz de dados para encontrar padrões e melhorar a eficiência da computação.

Se você estiver interessado em ler sobre outras equações importantes e conhecidas na ciência de dados e no aprendizado de máquina, confira nosso tutorial Equação normal para regressão linear. O DataCamp também oferece ótimos cursos para que você tenha um caminho de aprendizado abrangente e estruturado, como o curso Álgebra linear para ciência de dados em R, que mencionei anteriormente e recomendo com certeza.