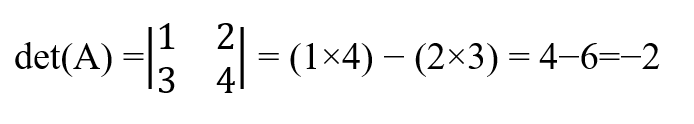El Determinante: Cómo funciona y qué nos dice

La información y los datos almacenados en una arquitectura informática están en forma de matrices. Por tanto, bajo la mayoría de los cálculos científicos y de aprendizaje automático subyacen matrices de diferentes dimensiones.

Las matrices son objetos matemáticos fundamentales en álgebra lineal. Las propias matrices tienen algunas propiedades, como la dimensión, la dispersión, los valores propios y los determinantes.

Un determinante es una propiedad fundamental de una matriz cuadrada que desempeña importantes funciones directas e indirectas en las operaciones matriciales, como la invertibilidad, la resolución de sistemas lineales en ingeniería y las transformaciones en geometría y gráficos por ordenador.

En este artículo, conocerás los determinantes de una matriz cuadrada, sus aplicaciones y algunos métodos para calcularlos a mano y con programas Python y R.

¿Qué es un determinante?

Un determinante es una función que mapea una matriz cuadrada en un escalar real (valor único). En matemáticas, el determinante de una matriz cuadrada A se indica como det(A) o |A|.

Como las propias matemáticas, el determinante tiene una larga historia que se remonta a los matemáticos chinos. En la antigua China, los matemáticos utilizaban determinantes para resolver sistemas de ecuaciones lineales (su método de resolución de ecuaciones lineales se denomina ahora Regla de Cramer). Más tarde, en la Europa del siglo XVI, el matemático Cardano puso de relieve los determinantes al aplicarlos en la solución de sistemas de ecuaciones lineales. Más tarde, Takakazu (siglo XVII), Leibniz (siglo XVII), Vandermonde , y Cauchy (siglo XVIII) establecieron el fundamento teórico de los determinantes en las matemáticas puras.

Propiedades de los determinantes

Aunque los determinantes deben calcularse para cada matriz cuadrada, tienen algunas propiedades conocidas en general y para algunas matrices concretas. Además, los determinantes sometidos a ciertas operaciones matemáticas también muestran algunos patrones y propiedades. Algunas de las propiedades conocidas de los determinantes son las siguientes:

El determinante de una matriz cuadrada idéntica es 1

Una matriz identidad tiene valores 1 en la diagonal y 0 en el resto.

Intercambiando dos filas o columnas cambiará el signo del determinante

Por ejemplo, en la matriz siguiente, el determinante es:

Si intercambiamos las filas, el resultado tiene un cambio de signo.

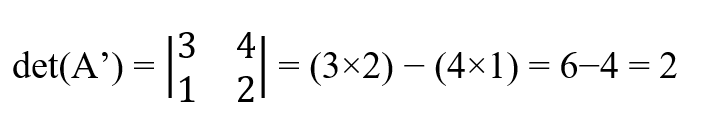
El determinante de las matrices triangulares es igual al producto de los elementos diagonales

Si una matriz es triangular inferior o superior, para calcular el determinante sólo tenemos que multiplicar los valores diagonales entre sí. Por ejemplo, en la siguiente matriz cuadrada triangular superior, el determinante se calcula multiplicando los valores diagonales:

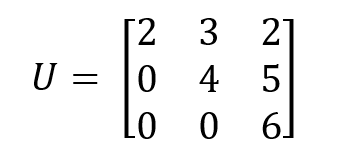
Basta con multiplicar los elementos diagonales para calcular el determinante: det(U)=2×4×6=48

El determinante es invariante por similitud matricial

Dos matrices son similares si se derivan de una transformación lineal y tienen bases diferentes. Si dos matrices son similares, entonces tienen el mismo determinante (y valores propios, trazas y polinomios característicos).

El determinante de un producto de matrices es el producto de los determinantes de las matrices.

A modo de ejemplo, aquí se muestran los determinantes individuales de las matrices A y B:

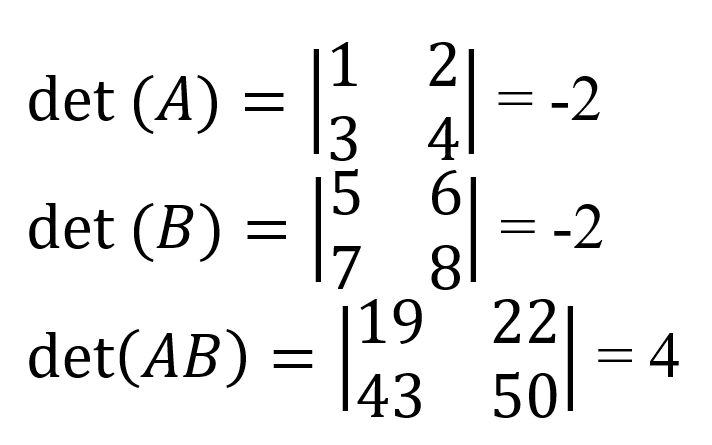
Los determinantes son invariantes por transposición

Por ejemplo, el determinante de la matriz A y AT es el mismo (-9).

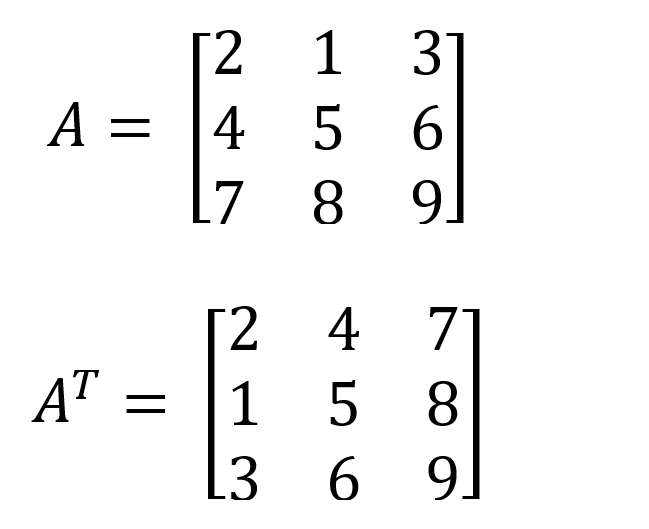
Métodos para calcular determinantes

Existen distintos métodos para calcular el determinante de una matriz cuadrada, como la fórmula de Leibniz, la expansión de Laplace y la eliminación de Gauss. La elección del método está sujeta al tamaño de la matriz y a los costes computacionales. A continuación describimos algunos de estos métodos:

Fórmula de Leibniz

La fórmula de Leibniz para hallar el determinante de una matriz cuadrada es la más adecuada para matrices pequeñas, sobre todo si el cálculo se realiza total o parcialmente a mano. La fórmula de Leibniz para hallar el determinante de una matriz es la siguiente:

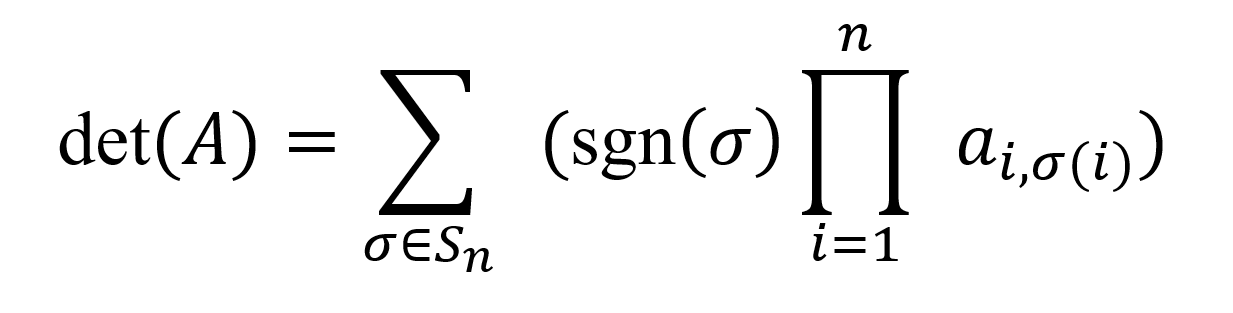
Donde Sn denota el conjunto de todas las permutaciones de los números 1,2,...,n y sgn(σ)es el signo de la permutación, que es +1 si la permutación es par y -1 si la permutación es impar. El término ai,σ es un elemento de la matriz A.

Expansión de Laplace

La expansión de Laplace es ideal para matrices grandes. En la expansión de Laplace o cofactorial, una matriz grande se divide en matrices más pequeñas. A continuación, se diseña un esquema en el que intervienen el determinante (menor) de una matriz más pequeña y su cofactor, y se itera sobre las filas o columnas.

Eliminación gaussiana

Como el determinante de una matriz triangular es el producto de sus elementos diagonales, reducir una matriz a una matriz diagonal hace que el cálculo del determinante sea más eficaz. En la eliminación gaussiana, se realizan una serie de operaciones de fila para reducir la matriz completa a la forma escalonada de fila o triangular superior. A continuación, se calcula el determinante multiplicando los elementos diagonales.

Cómo hallar el determinante de matrices de distintos tamaños

En los ejemplos siguientes, aplicamos cada uno de los métodos anteriores a matrices de distintos tamaños para hallar los determinantes.

Cómo hallar el determinante de una matriz de 2x2

El determinante de una matriz cuadrada de 2x2 es el más fácil de recordar y calcular. Si denotamos una matriz A de 2x2 como: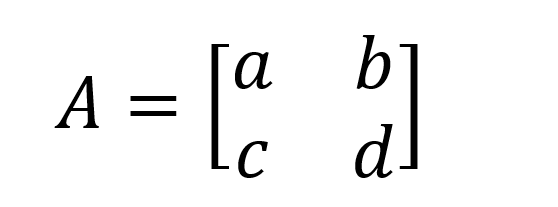 

Entonces det(A) = (a x d) - (b x c). Por ejemplo, para la matriz B

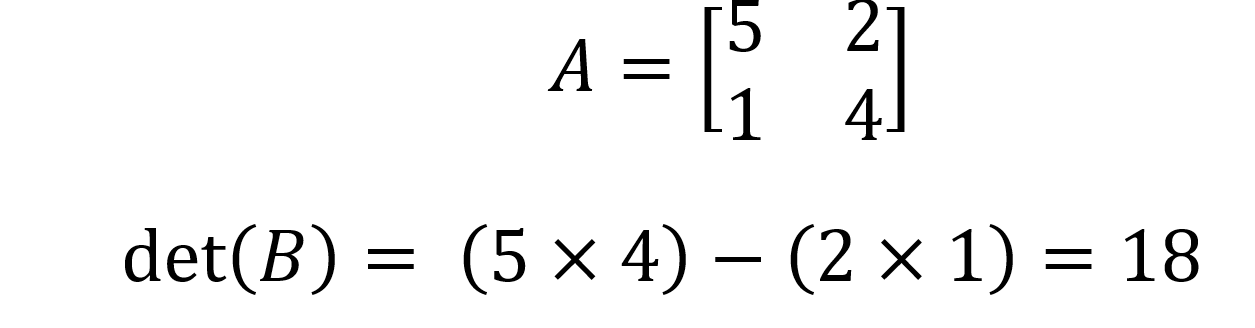
Cómo hallar el determinante de una matriz 3x3

Aunque existe una fórmula para el cálculo de una matriz cuadrada de 3x3, por razones pedagógicas demostramos la expansión de Laplace (cofactor) en este ejemplo. A continuación calcularemos el determinante de la matriz A:

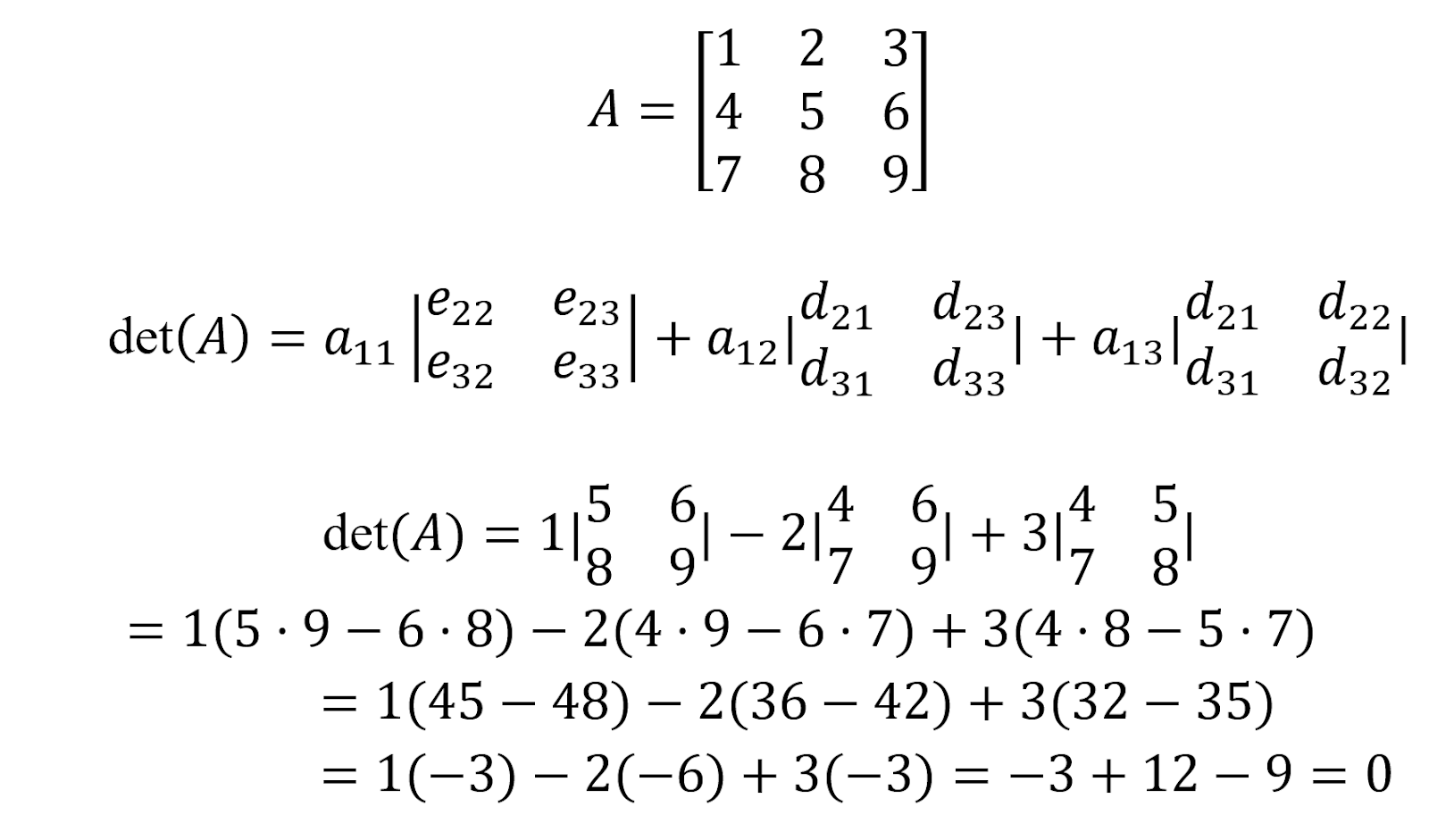
Cómo hallar el determinante de una matriz 4x4

Aprovechamos ahora la ocasión para mostrar el método de eliminación de Gauss para calcular el determinante de una matriz A de 4 x 4 a continuación: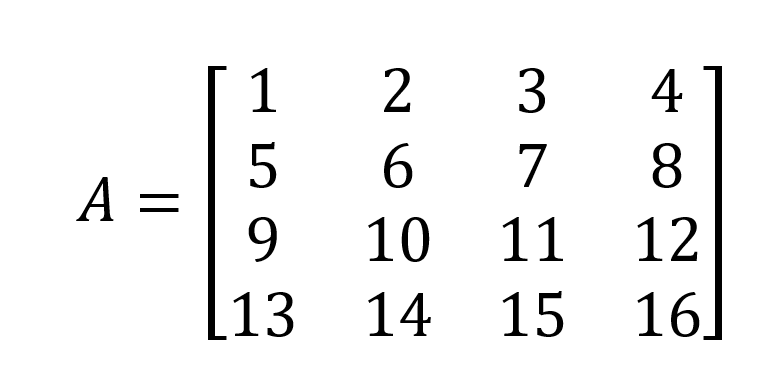

Transformaremos esta matriz en una matriz triangular superior realizando operaciones de fila.

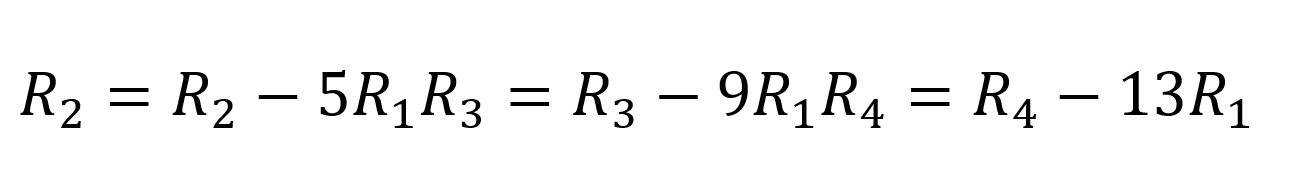
Obtenemos,

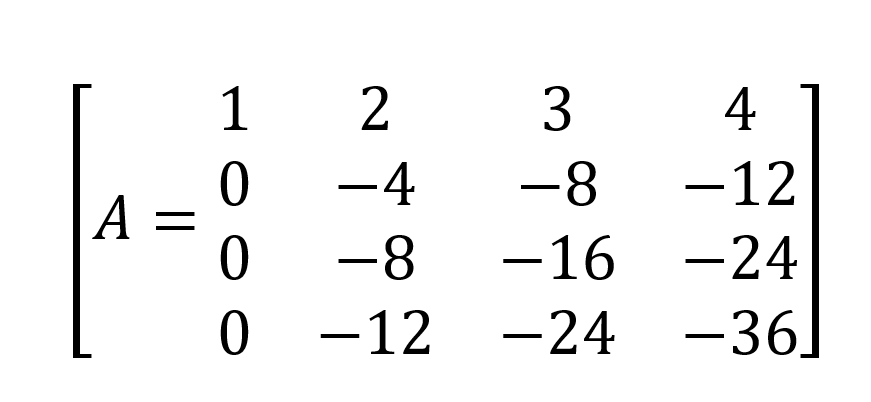
Una operación de fila más:

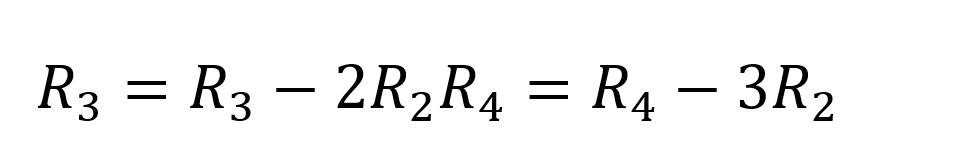
Obtenemos, 

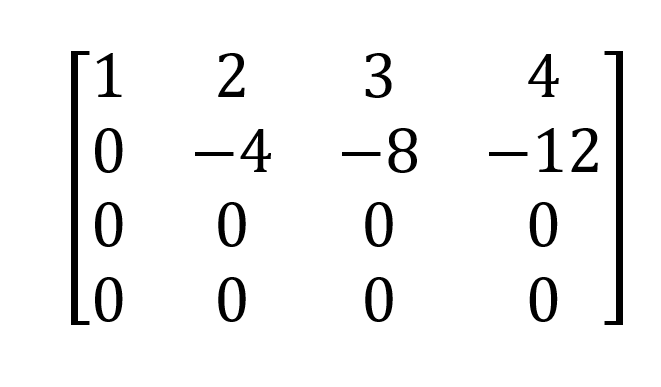
Y el determinante es el producto de los elementos diagonales:

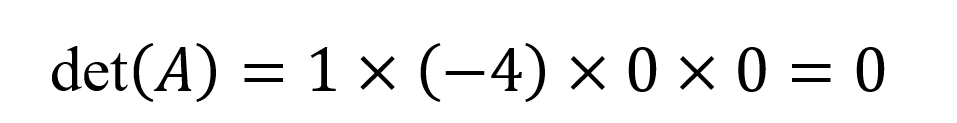
Significado geométrico y algebraico

Como hemos definido anteriormente, un determinante es una función que asigna una matriz cuadrada a un número real.

En geometría, un cuadrado consta de dos lados, cuyo producto es la superficie. Y si hay tres lados, obtenemos el volumen. El (valor absoluto del) determinante de una matriz de 2 x 2 puede interpretarse como el área de un paralelogramo formado por las dos columnas de la matriz (como vectores direccionales), y el determinante con signo de una matriz de 3 x 3 puede interpretarse como el volumen de un paralelepípedo (sólido tridimensional).

En las transformaciones gráficas, como estirar o encoger una imagen, el determinante de la imagen transformada muestra si el área de la imagen original (matriz) ha cambiado o no (principio de Cavalieri) tras la transformación, mientras que los valores propios muestran si la imagen se ha extendido o encogido con o sin cambio de área.

Los determinantes también pueden indicar si las columnas o filas de una matriz son combinaciones lineales entre sí (redundancia) o son linealmente independientes, cada una con información única. Si el determinante de una matriz es distinto de cero, concluimos que las columnas o filas de la matriz son linealmente independientes. Si el determinante es cero, muestra que las columnas (o filas) de la matriz son linealmente dependientes.

Por último, los determinantes también se utilizan en la formulación del polinomio característico para calcular los valores propios.

El Determinante en Python y R

Aunque calcular determinantes a mano es una valiosa experiencia de aprendizaje para afinar nuestras habilidades matemáticas y desarrollar la sofisticación matemática, con el tiempo las limitaciones de tiempo y energía pueden hacer que utilicemos una calculadora o un lenguaje de programación, como Python o R. Tanto Python como R proporcionan bibliotecas, funciones o métodos para calcular el determinante de una matriz. En los siguientes fragmentos de código, demostramos cómo calcular el determinante de una matriz utilizando Python y R.

Ejemplo en Python

Dos paquetes populares de Python para calcular el determinante de una matriz son Numpy y Sympy (Symbolic Python). En el siguiente fragmento de código, mostramos cómo calcular el determinante utilizando las bibliotecas Numpy y Sympy en Python.

# Computing determinant using Numpy
import numpy as np
matrix = np.array([[1, 2], [3, 4]])
determinant = np.linalg.det(matrix)
print("Determinant:", determinant)
 
# Computing determinant using Sympy# Import the necessary library
import sympy as sp
matrix = sp.Matrix([[1, 2], [3, 4]])
determinant = matrix.det()
print("Determinant:", determinant)
 

R ejemplo

Calcular el determinante de una matriz en R no requiere cargar una biblioteca. La base R proporciona una función incorporada para calcular el determinante de una matriz, como se muestra en el siguiente fragmento de código R:

matrix <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
determinant <- det(matrix)
print(paste("Determinant:", determinant))

Aplicaciones de los Determinantes

Sistemas lineales

Los determinantes pueden utilizarse directamente para resolver un sistema de ecuaciones lineales mediante la regla de Cramer. Por la regla de Cramer, primero construimos una matriz formada por los coeficientes de las incógnitas del sistema de ecuaciones y calculamos su determinante. A continuación, formamos una matriz para cada incógnita y calculamos su determinante. El cociente entre el determinante de la nueva matriz y la matriz matriz será el valor de la incógnita.

Ecuaciones diferenciales

Una ecuación diferencial puede tener varias soluciones (funciones). Para asegurarnos de que las soluciones son linealmente independientes (únicas), se calculan los determinantes del conjunto de soluciones de la función, llamado Wronskiano. Un Wronskiano distinto de cero indica que las funciones / soluciones son linealmente independientes en el intervalo dado.

Geometría

En geometría, el determinante de una matriz de 2 x 2 puede interpretarse como el área de un paralelogramo, y el determinante de una matriz de 3 x 3 puede interpretarse como el volumen de un sólido (paralelepípedo).  Los determinantes en el mapeo de funciones multivariables pueden ayudar a comprender si el mapeo ha afectado al área o al volumen de las funciones utilizando el determinante de la matriz jacobiana.

Puntos clave que debes recordar

Los determinantes desempeñan un papel más indirecto en el aprendizaje automático, la estadística y la informática científica. Sin embargo, comprender cómo utilizan los determinantes los sistemas de ecuaciones lineales, la inversión de matrices, la infografía y las ecuaciones diferenciales puede arrojar luz sobre su sutil significado y la necesidad de comprender los determinantes. La próxima vez que te encuentres con un error de matriz invertible, podrías pensar en el papel del determinante en la forma y la independencia lineal de la matriz.

Conclusión

Espero que hayas llegado a apreciar la importancia del determinante para comprender el comportamiento y las transformaciones de las matrices. Nuestro curso de Álgebra Lineal para la Ciencia de Datos en R es un gran paso para seguir aprendiendo técnicas de álgebra lineal y aplicarlas en los flujos de trabajo de la ciencia de datos.