Die Determinante: Wie es funktioniert und was es uns sagt

Informationen und Daten, die in einer Computerarchitektur gespeichert werden, liegen in Form von Matrizen vor. Daher liegen den meisten wissenschaftlichen, maschinellen Lern- und Berechnungsprozessen Matrizen unterschiedlicher Dimensionen zugrunde.

Matrizen sind grundlegende mathematische Objekte in der linearen Algebra. Matrizen selbst haben einige Eigenschaften, wie Dimension, Sparsamkeit, Eigenwerte und Determinanten.

Die Determinante ist eine grundlegende Eigenschaft einer quadratischen Matrix, die eine wichtige direkte und indirekte Rolle bei Matrixoperationen spielt, z. B. bei der Invertierbarkeit, beim Lösen linearer Systeme in der Technik und bei Transformationen in der Geometrie und Computergrafik.

In diesem Artikel lernst du die Determinanten einer quadratischen Matrix, ihre Anwendungen und einige Methoden kennen, um sie von Hand und mit Python und R-Programmen zu berechnen.

Was ist eine Determinante?

Eine Determinante ist eine Funktion, die eine quadratische Matrix auf einen reellen Skalar (Einzelwert) abbildet. In der Mathematik wird die Determinante einer quadratischen Matrix A als det(A) oder |A| dargestellt.

Wie die Mathematik selbst hat auch die Determinante eine lange Geschichte, die bis zu den chinesischen Mathematikern zurückreicht. Im alten China benutzten Mathematiker Determinanten, um lineare Gleichungssysteme zu lösen (ihre Methode zum Lösen linearer Gleichungen wird heute Cramer's Rule genannt). Später in Europa, im 16. Jahrhundert, brachte der Mathematiker Cardano die Determinanten in den Vordergrund, indem er sie bei der Lösung von linearen Gleichungssystemen einsetzte. Später legten Takakazu (17. Jahrhundert), Leibniz (17. Jahrhundert), Vandermonde und Cauchy (18. Jahrhundert) die theoretischen Grundlagen der Determinanten in der reinen Mathematik.

Eigenschaften von Determinanten

Obwohl die Determinanten für jede quadratische Matrix berechnet werden müssen, haben sie einige bekannte Eigenschaften im Allgemeinen und für einige spezielle Matrizen. Außerdem zeigen Determinanten, die bestimmten mathematischen Operationen unterliegen, auch einige Muster und Eigenschaften. Einige der bekannten Eigenschaften von Determinanten sind die folgenden:

Die Determinante einer quadratischen Identitätsmatrix ist 1

Eine Identitätsmatrix hat auf der Diagonalen den Wert 1 und sonst 0.

Das Vertauschen zweier Zeilen oder Spalten ändert das Vorzeichen der Determinante

In der folgenden Matrix ist die Determinante zum Beispiel:

Wenn wir die Zeilen vertauschen, ändert sich das Vorzeichen des Ergebnisses.

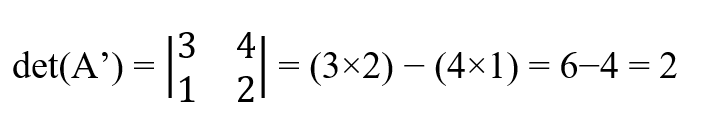
Die Determinante von Dreiecksmatrizen ist gleich dem Produkt der Diagonalelemente

Wenn eine Matrix unter- oder oberdreieckig ist, müssen wir zur Berechnung der Determinante nur die Diagonalwerte miteinander multiplizieren. In der folgenden oberen dreieckigen Quadratmatrix wird die Determinante zum Beispiel durch Multiplikation der Diagonalwerte berechnet:

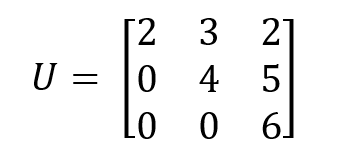
Wir multiplizieren einfach die Diagonalelemente, um die Determinante zu berechnen: det(U)=2×4×6=48

Die Determinante ist invariant unter Matrixähnlichkeit

Zwei Matrizen sind ähnlich, wenn sie von einer linearen Transformation abgeleitet sind und unterschiedliche Basen haben. Wenn zwei Matrizen ähnlich sind, dann haben sie die gleiche Determinante (und Eigenwerte, Spuren und charakteristische Polynome).

Die Determinante eines Matrixprodukts ist das Produkt der Determinanten der Matrizen.

Als Beispiel werden hier die einzelnen Determinanten der Matrizen A und B gezeigt:

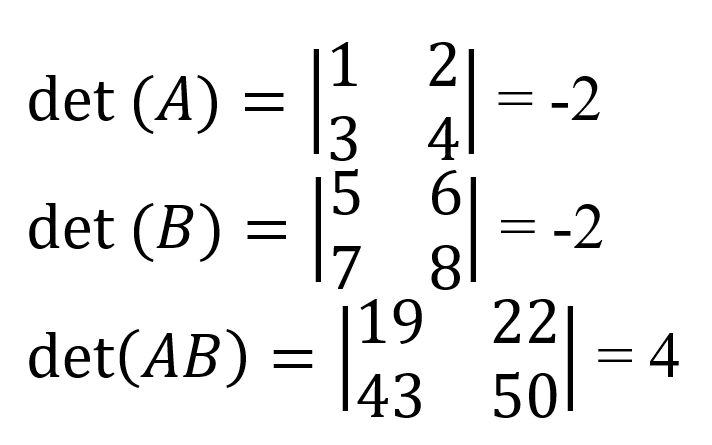
Determinanten sind invariant unter Transposition

Zum Beispiel ist die Determinante der Matrix A und AT ist die gleiche (-9).

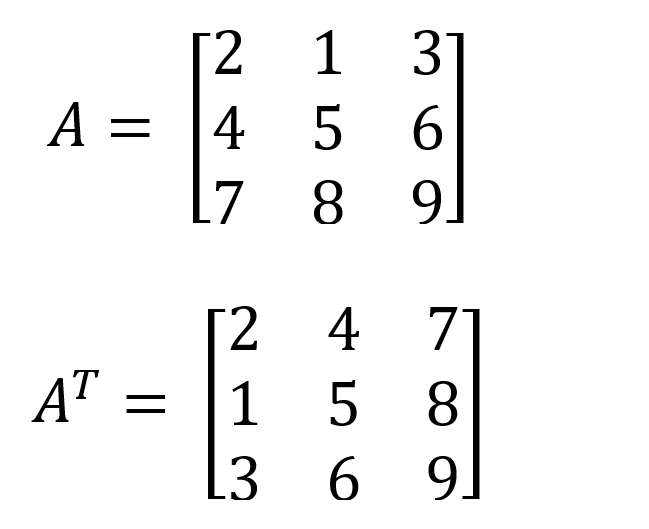
Methoden zur Berechnung der Determinanten

Es gibt verschiedene Methoden, um die Determinante einer quadratischen Matrix zu berechnen, z. B. die Leibniz-Formel, die Laplace-Erweiterung und die Gaußsche Elimination. Die Wahl der Methode ist abhängig von der Größe der Matrix und den Rechenkosten. Im Folgenden beschreiben wir einige dieser Methoden:

Leibniz formula

Die Leibniz-Formel zur Bestimmung der Determinante einer quadratischen Matrix eignet sich am besten für kleine Matrizen, vor allem, wenn die Berechnung ganz oder teilweise von Hand durchgeführt wird. Die Leibniz-Formel zur Ermittlung der Determinante einer Matrix lautet wie folgt:

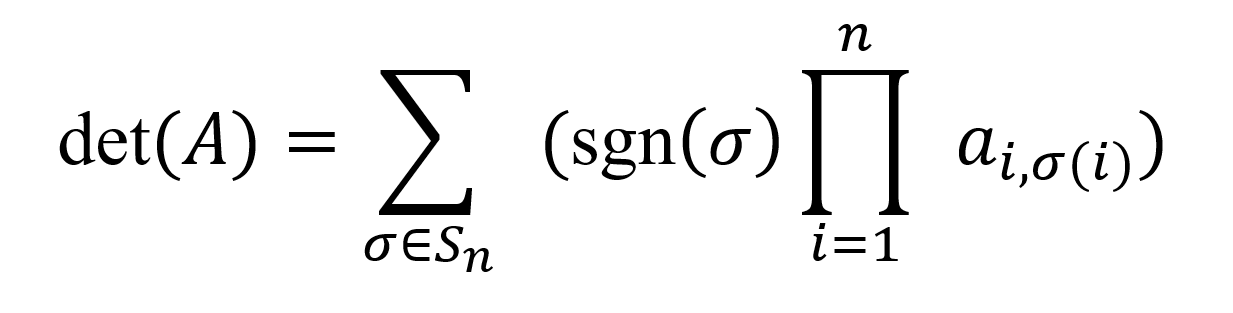
Wobei Sn die Menge aller Permutationen der Zahlen 1,2,...,n bezeichnet und sgn(σ) das Vorzeichen der Permutation ist, das +1 ist, wenn die Permutation gerade ist, und -1, wenn die Permutation ungerade ist. Der Term ai,σ ist ein Element der Matrix A.

Laplace-Erweiterung

Die Laplace-Erweiterung ist ideal für größere Matrizen. Bei der Laplace- oder Kofaktor-Erweiterung wird eine große Matrix in kleinere Matrizen unterteilt. Dann wird ein Schema mit der Determinante (Minor) einer kleineren Matrix und ihrem Kofaktor entworfen und über Zeilen oder Spalten hinweg iteriert.

Gaußsche Eliminierung

Da die Determinante einer Dreiecksmatrix das Produkt ihrer Diagonalelemente ist, macht die Reduzierung einer Matrix auf eine Diagonalmatrix die Berechnung der Determinante effizienter. Bei der Gauß'schen Eliminierung wird eine Reihe von Zeilenoperationen durchgeführt, um die vollständige Matrix auf die Zeilen-Echelon- oder obere Dreiecksform zu reduzieren. Dann wird die Determinante durch Multiplikation der Diagonalelemente berechnet.

So findest du die Determinante für Matrizen unterschiedlicher Größe

In den folgenden Beispielen wenden wir jede der oben genannten Methoden auf unterschiedlich große Matrizen an, um die Determinanten zu bestimmen.

Wie man die Determinante einer 2x2-Matrix findet

Die Determinante einer quadratischen 2x2-Matrix ist am einfachsten zu merken und zu berechnen. Wenn wir eine 2x2-Matrix A wie folgt bezeichnen: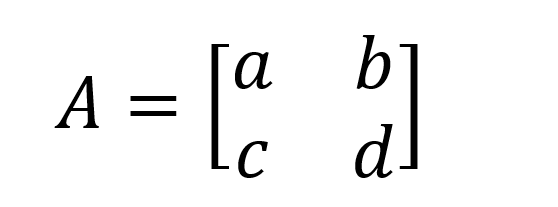 

Dann ist det(A) = (a x d) - (b x c). Zum Beispiel für Matrix B unten:

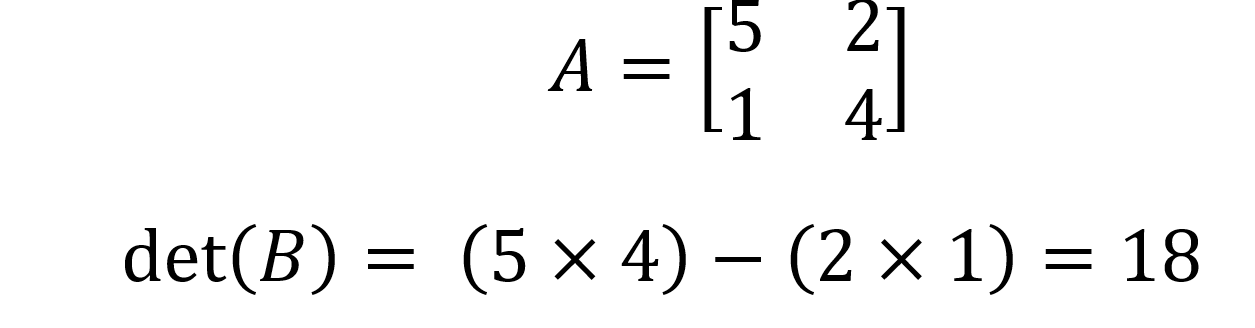
Wie man die Determinante einer 3x3-Matrix findet

Obwohl es eine Formel für die Berechnung einer 3x3-Quadratmatrix gibt, zeigen wir in diesem Beispiel aus pädagogischen Gründen die Laplace-Erweiterung (Kofaktor). Im Folgenden werden wir die Determinante der Matrix A berechnen:

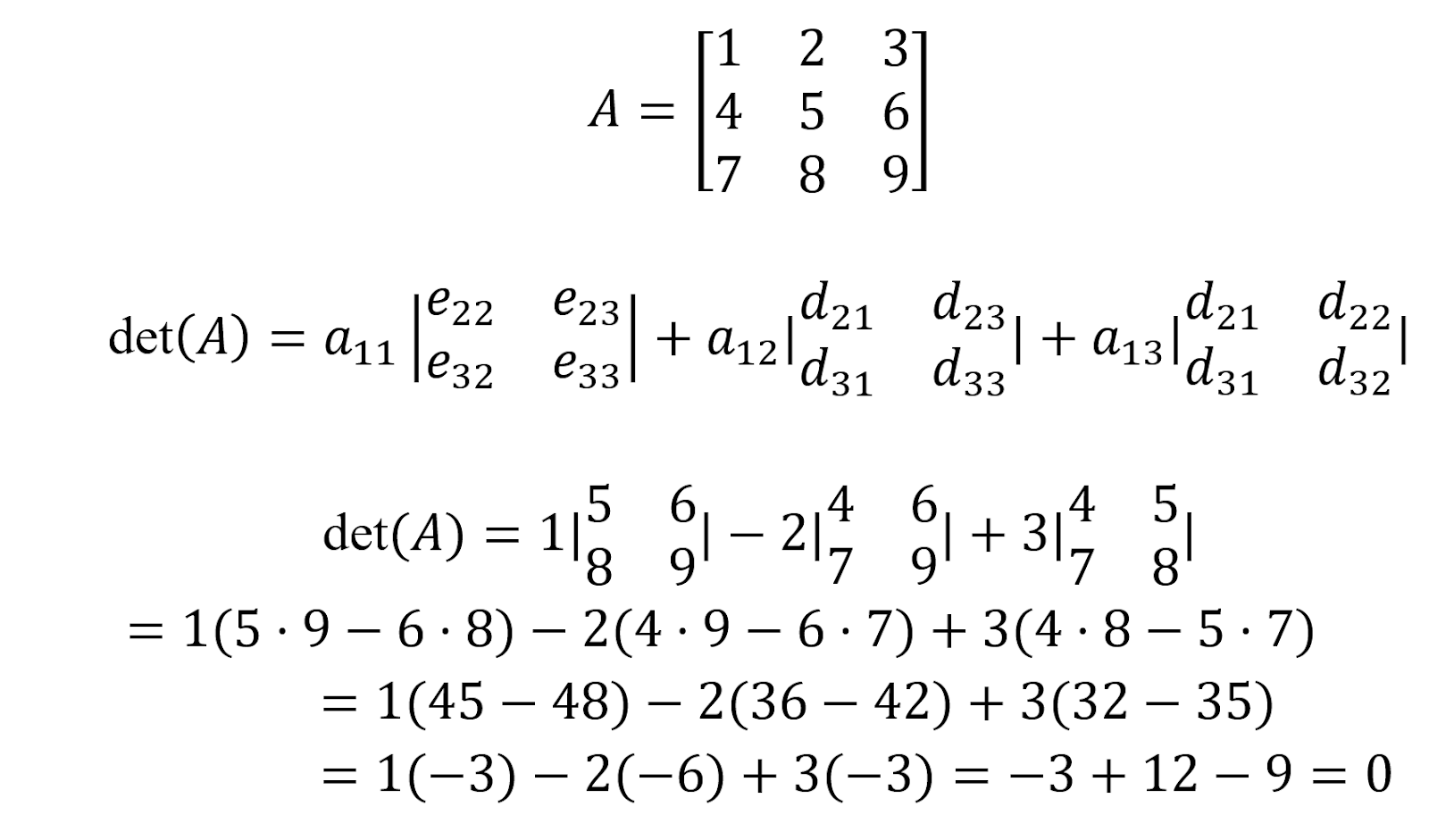
Wie man die Determinante einer 4x4-Matrix findet

Wir nutzen nun die Gelegenheit, um die Gaußsche Eliminierungsmethode zur Berechnung der Determinante einer 4 x 4 Matrix A zu zeigen: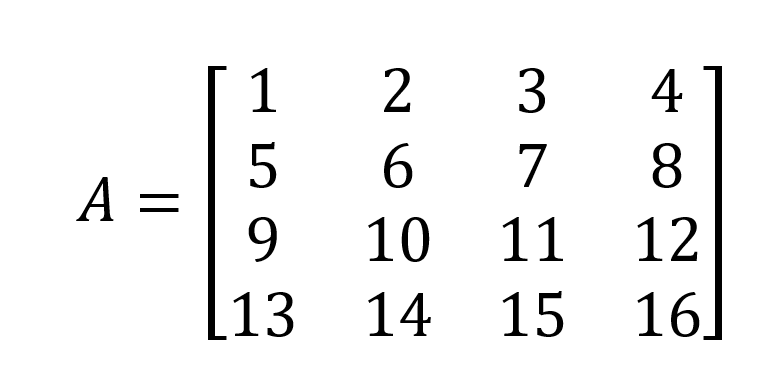

Wir werden diese Matrix in eine obere Dreiecksmatrix umwandeln, indem wir Zeilenoperationen durchführen.

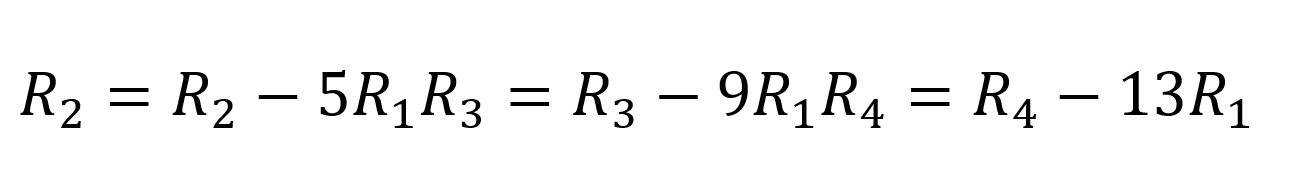
Wir bekommen,

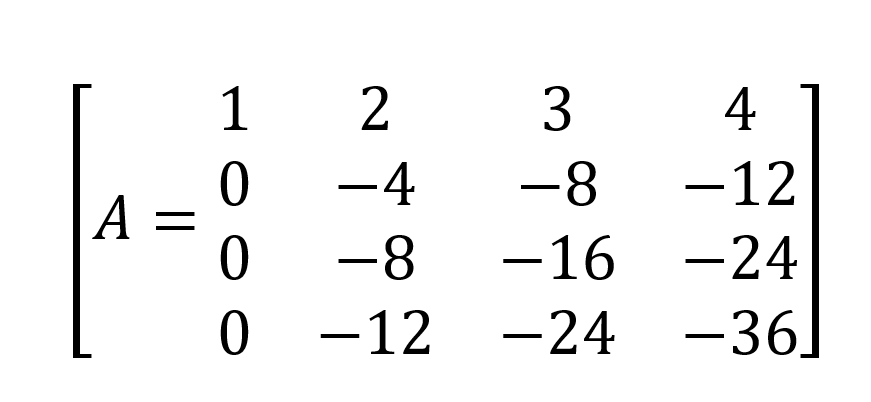
Eine weitere Reihenoperation:

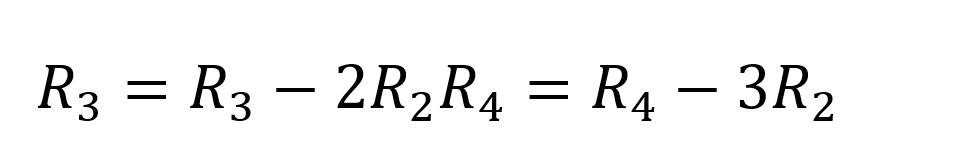
Wir bekommen, 

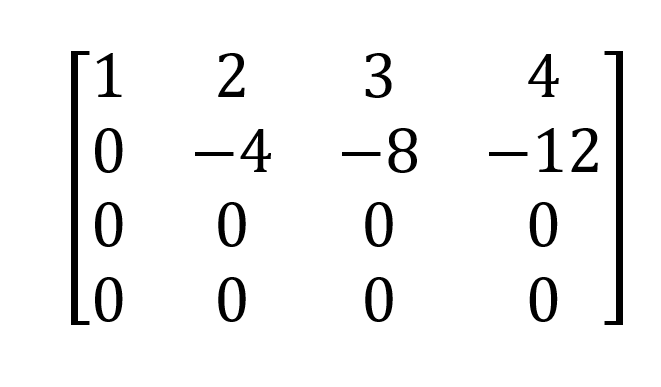
Und die Determinante ist das Produkt der Diagonalelemente:

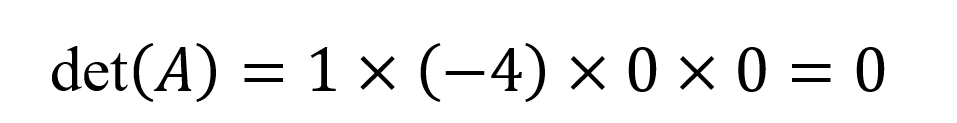
Geometrische und algebraische Signifikanz

Wie wir oben definiert haben, ist eine Determinante eine Funktion, die eine quadratische Matrix auf eine reelle Zahl abbildet.

In der Geometrie besteht ein Quadrat aus zwei Seiten, deren Produkt die Fläche ist. Und wenn es drei Seiten gibt, erhalten wir das Volumen. Der (absolute Wert) der Determinante einer 2 x 2-Matrix kann als Fläche eines Parallelogramms interpretiert werden, das durch die beiden Spalten der Matrix (als Richtungsvektoren) gebildet wird, und die vorzeichenbehaftete Determinante einer 3 x 3-Matrix kann als Volumen eines Parallelepipeds (dreidimensionaler Körper) interpretiert werden.

Bei grafischen Transformationen, wie z. B. dem Dehnen oder Schrumpfen eines Bildes, zeigt die Determinante des transformierten Bildes, ob sich die Fläche des ursprünglichen Bildes (Matrix) nach der Transformation verändert hat oder nicht (Cavalieri-Prinzip), während die Eigenwerte zeigen, ob sich das Bild mit oder ohne Veränderung der Fläche vergrößert oder verkleinert hat.

Determinanten können auch angeben, ob die Spalten oder Zeilen einer Matrix linear miteinander kombiniert sind (Redundanz) oder ob sie linear unabhängig sind und jeweils eine eindeutige Information enthalten. Wenn die Determinante einer Matrix ungleich Null ist, schließen wir daraus, dass die Spalten oder Zeilen der Matrix linear unabhängig sind. Wenn die Determinante Null ist, zeigt das, dass die Spalten (oder Zeilen) der Matrix linear abhängig sind.

Schließlich werden Determinanten auch bei der Formulierung des charakteristischen Polynoms zur Berechnung der Eigenwerte verwendet.

Die Determinante in Python und R

Obwohl das Berechnen von Determinanten von Hand eine wertvolle Lernerfahrung ist, um unsere mathematischen Fähigkeiten zu schärfen und mathematische Raffinesse zu entwickeln, kann es sein, dass wir aus Zeit- und Energiegründen einen Taschenrechner oder eine Programmiersprache wie Python oder R verwenden müssen. Sowohl Python als auch R bieten Bibliotheken, Funktionen oder Methoden zur Berechnung der Determinante einer Matrix. In den folgenden Codeschnipseln zeigen wir, wie man die Determinante einer Matrix mit Python und R berechnet.

Python Beispiel

Zwei beliebte Python-Pakete zum Berechnen der Determinante einer Matrix sind Numpy und Sympy (Symbolic Python). Im folgenden Codeschnipsel zeigen wir, wie du die Determinante mit den Bibliotheken Numpy und Sympy in Python berechnest.

# Computing determinant using Numpy
import numpy as np
matrix = np.array([[1, 2], [3, 4]])
determinant = np.linalg.det(matrix)
print("Determinant:", determinant)
 
# Computing determinant using Sympy# Import the necessary library
import sympy as sp
matrix = sp.Matrix([[1, 2], [3, 4]])
determinant = matrix.det()
print("Determinant:", determinant)
 

R Beispiel

Um die Determinante einer Matrix in R zu berechnen, muss keine Bibliothek geladen werden. R bietet eine eingebaute Funktion, um die Determinante einer Matrix zu berechnen, wie im folgenden R-Codeausschnitt gezeigt wird:

matrix <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
determinant <- det(matrix)
print(paste("Determinant:", determinant))

Anwendungen von Determinanten

Lineare Systeme

Determinanten können direkt verwendet werden, um ein lineares Gleichungssystem mit der Cramerschen Regel zu lösen. Nach der Cramerschen Regel konstruieren wir zunächst eine Matrix, die aus den Koeffizienten der Unbekannten im Gleichungssystem besteht, und berechnen ihre Determinante. Als Nächstes bilden wir für jede Unbekannte eine Matrix und berechnen ihre Determinante. Das Verhältnis der Determinante der neuen Matrix zur Muttermatrix ist der Wert der Unbekannten.

Differentialgleichungen

Eine Differentialgleichung kann mehrere Lösungen (Funktionen) haben. Um sicherzustellen, dass die Lösungen linear unabhängig (eindeutig) sind, werden die Determinanten der Menge der Funktionslösungen, die sogenannte Wronskian, berechnet. Ein Wronskianer ungleich Null bedeutet, dass die Funktionen/Lösungen in dem gegebenen Intervall linear unabhängig sind.

Geometrie

In der Geometrie kann die Determinante einer 2 x 2-Matrix als Fläche eines Parallelogramms und die Determinante einer 3 x 3-Matrix als Volumen eines Körpers (Parallelepipedes) interpretiert werden.  Determinanten bei der Abbildung multivariabler Funktionen können helfen zu verstehen, ob die Abbildung die Fläche oder das Volumen der Funktionen beeinflusst hat, indem die Determinante der Jacobimatrix verwendet wird.

Wichtige Punkte zur Erinnerung

Beim maschinellen Lernen, in der Statistik und im wissenschaftlichen Rechnen spielen Determinanten eine eher indirekte Rolle. Wenn du jedoch verstehst, wie lineare Gleichungssysteme, Matrixinversion, Computergrafik und Differentialgleichungen Determinanten verwenden, kannst du ihre subtile Bedeutung und die Notwendigkeit, Determinanten zu verstehen, besser einschätzen. Wenn du das nächste Mal auf einen invertierbaren Matrixfehler stößt, solltest du über die Rolle der Determinante für die Form und die lineare Unabhängigkeit der Matrix nachdenken.

Fazit

Ich hoffe, du hast verstanden, wie wichtig die Determinante für das Verständnis von Matrixverhalten und -umwandlungen ist. Unser Kurs Lineare Algebra für Data Science in R ist ein großartiger nächster Schritt, um die Techniken der linearen Algebra weiter zu erlernen und sie in Data Science Workflows anzuwenden.