Guia do cientista de dados para processamento de sinais

Introdução ao processamento de sinais

O processamento de sinais é uma disciplina fundamental da ciência de dados que lida com a extração, a análise e a manipulação de sinais e dados de séries temporais. É um campo amplo que pode se tornar complexo. Este guia apresentará os conceitos básicos e as ideias necessárias para ajudá-lo a navegar pelos sinais de processamento, sejam eles dados de sensores de pressão ou tendências do mercado de ações.

O que são sinais e dados de séries temporais?

No contexto do processamento de sinais, um sinal refere-se a qualquer forma de informação que varia ao longo do tempo ou do espaço. Os sinais podem assumir várias formas, desde formas de onda de áudio e leituras de temperatura até dados do mercado financeiro e medições de sensores.

Os dados de séries temporais são um subconjunto de sinais em que as medições são registradas em pontos sucessivos no tempo. Os sinais podem ser analógicos (contínuos) ou digitais (discretos).

Sinais de tempo contínuo vs. sinais de tempo discreto

Os dados de sinais podem ser classificados em dois tipos principais: contínuos e discretos.

Sinais contínuos são aqueles medidos e registrados em uma faixa contínua, incluindo sinais analógicos, como ondas sonoras e medições de temperatura (de termômetros analógicos).

Os sinais discretos são registrados em pontos específicos e distintos. Esse tipo de dados é mais comum em aplicações práticas devido à natureza discreta da aquisição e do armazenamento de dados atuais.

Medições de sensores digitais e dados do mercado financeiro amostrados em intervalos fixos são exemplos de sinais de tempo discreto.

A importância do processamento de sinais na ciência de dados

Muitas vezes, os dados brutos do sinal são difíceis de interpretar.

Imagine ver os dados de ondas sonoras de um podcast, por exemplo. O processamento de sinais nos permite extrair percepções valiosas desses dados brutos que podem não ser aparentes à primeira vista. Essas informações podem ser usadas para tomar decisões informadas, identificar oportunidades ou resolver problemas complexos em vários domínios.

O processamento de sinais também é útil durante o pré-processamento de dados.

Os dados do mundo real costumam ser ruidosos, e as técnicas de processamento de sinais permitem que os cientistas de dados removam perturbações indesejadas, outliers e artefatos, resultando em conjuntos de dados mais limpos e confiáveis. Esses dados limpos são essenciais para modelagem precisa, previsões e outras tarefas avançadas de análise de dados. Além disso, o processamento de sinais está no centro de muitos algoritmos e modelos avançados usados na ciência de dados, como previsão de séries temporais, detecção de anomalias e reconhecimento de imagem e fala.

Figura 1: Imagem artística que representa o audiograma (frequências de som) de um podcaster. Esse tipo de audiograma é um exemplo de sinal. Crédito da foto: DALL-E.

Dados de séries temporais

Os dados de séries temporais são um tipo de sinal ordenado temporalmente, em que cada ponto de dados está associado a um registro de data e hora específico. Essa estrutura temporal permite a análise de tendências, sazonalidade e padrões cíclicos. Há vários recursos disponíveis para análise de dados de séries temporais em Python e séries temporais com R.

Previsão de séries temporais e extração de recursos para aprendizado de máquina

A previsão de séries temporais é um subcampo do processamento de sinais que visa prever valores futuros com base em pontos de dados históricos. A previsão desempenha um papel crucial em vários setores, permitindo que as empresas tomem decisões informadas, otimizem a alocação de recursos e antecipem as tendências do mercado. Envolve a análise de padrões e tendências em dados de séries temporais para tentar prever etapas futuras.

Para obter uma visão detalhada da previsão de séries temporais, consulte o Tutorial de previsão de séries temporais.

Técnicas de visualização de dados de sinais

Os sinais geralmente são mais bem compreendidos por meio de recursos visuais. Há alguns gráficos que geralmente são usados para diferentes tipos de dados de sinal.

Os gráficos de linha são uma maneira simples, porém eficiente, de visualizar dados de sinal, em que o eixo y representa o valor do sinal e o eixo x corresponde a alguma métrica sequencial, como tempo, metros ou número de amostra. Esses gráficos podem fornecer uma compreensão imediata das tendências e flutuações.

Uma forma de onda de áudio é uma maneira comum de visualizar o som. Você pode ter visto esses tipos de gráficos ao reproduzir música ou ouvir um podcast, pois vários aplicativos de música os exibem em tempo real.

Outra visualização comum é um espectrograma ou um audiograma. E os dados de ações geralmente são exibidos como uma série de boxplots, chamados de candlesticks, para exibir tendências ao longo do tempo.

Figura 3: Um exemplo de uma forma de onda de áudio que descreve o som. Crédito da imagem: DALL-E.

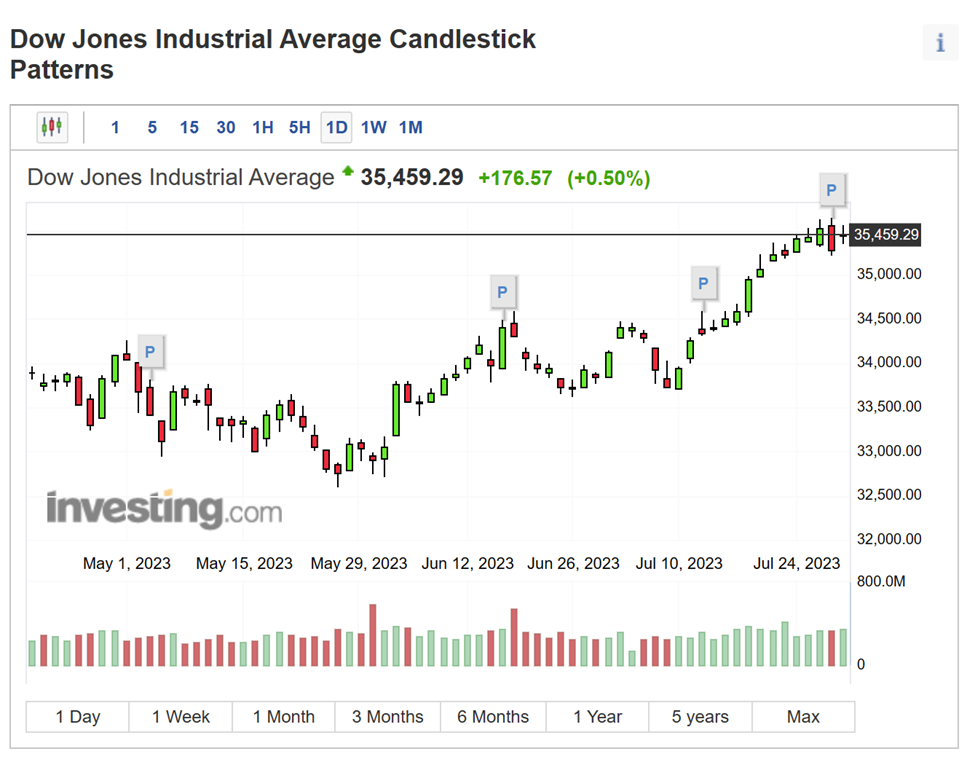
Figura 4: Um exemplo de gráfico de velas usado para análise do mercado de ações. Fonte da imagem

Ferramentas para processamento de sinais

Introdução ao MATLAB e Python para processamento de sinais

No âmbito do processamento de sinais e da análise de séries temporais, duas ferramentas de programação comumente usadas são o MATLAB e o Python.

O MATLAB, desenvolvido pela MathWorks, é uma ferramenta poderosa e versátil amplamente utilizada em engenharia, matemática e pesquisa científica. Sua extensa documentação, funções integradas para processamento de sinais, interface amigável e recursos de visualização fazem dele uma excelente opção. A principal desvantagem é o preço da ferramenta.

Se você estiver interessado em usar o MATLAB para processamento de sinais, consulte a Signal Processing Toolbox e a Audio Toolbox, ambas com ampla documentação e exemplos interativos.

O Python é uma alternativa gratuita usada por muitos cientistas de dados para tarefas de processamento de sinais. Se estiver interessado em mudar do Matlab para o Python, confira este curso Python para usuários do MATLAB da DataCamp!

Bibliotecas como NumPy, Pandas e SciPy oferecem suporte para análise de dados de séries temporais. Embora haja uma grande quantidade de documentação sobre Python, sua natureza de código aberto pode tornar difícil encontrar a documentação necessária para sua tarefa específica.

Para tarefas de processamento de sinais, eu recomendaria este repositório do Github.

Técnicas de pré-processamento e filtragem no processamento de sinais

O pré-processamento de dados é uma etapa crucial no processamento de sinais que estabelece a base para uma análise precisa e significativa. Dependendo dos seus dados e da sua análise, isso pode significar lidar com dados irregulares ou ausentes por meio de métodos de reamostragem e interpolação ou suavizar os dados usando vários filtros.

Como lidar com dados irregulares ou ausentes: reamostragem e interpolação

Ao trabalhar com dados de sinal, você pode encontrar intervalos de amostragem irregulares ou pontos de dados ausentes, o que pode frustrar seus esforços de análise e modelagem.

A reamostragem é uma técnica que você pode usar para padronizar os intervalos dos dados. Isso pode envolver o aumento da amostragem (aumentando a frequência dos pontos de dados) ou a redução da amostragem (diminuindo a frequência dos pontos de dados) para obter uma série temporal regular.

Os métodos de interpolação entram em ação quando faltam pontos de dados ou precisam ser estimados. As técnicas comuns de interpolação incluem interpolação linear, interpolação spline e interpolação baseada em tempo.

Esses métodos preenchem as lacunas nos dados estimando os valores com base nos pontos de dados adjacentes, permitindo a obtenção de dados de sinal contínuos e suaves.

Em sua essência, a reamostragem e a interpolação usam essencialmente o mesmo conceito para obter resultados diferentes. Ambos estão interpretando um padrão nos dados e "adivinhando" como os dados seriam ao longo desse padrão, embora usem meios diferentes para fazer isso.

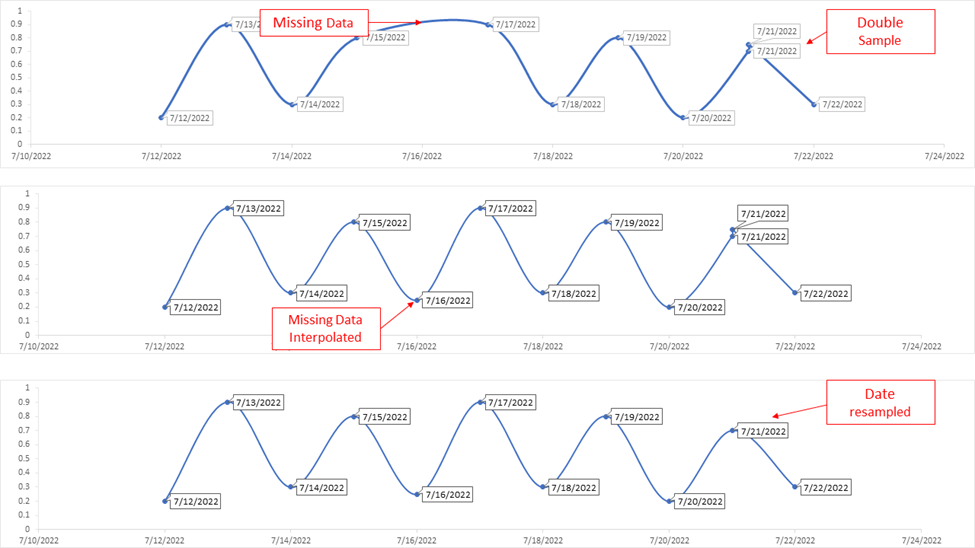
Figura 5: Esta figura mostra um exemplo muito simplificado de como a interpolação e a reamostragem podem limpar dados confusos.

Manuseio de ruídos e outliers

Ruído e outliers são ocorrências comuns em dados de sinais e podem dificultar a obtenção de insights.

Os outliers são pontos de dados que se desviam significativamente do padrão geral, enquanto o ruído se refere a flutuações aleatórias nos dados que podem obscurecer os padrões subjacentes.

Os valores atípicos podem ser gerenciados por meio de técnicas como truncamento de dados ou winsorização, que envolvem limitar os valores extremos a um determinado limite.

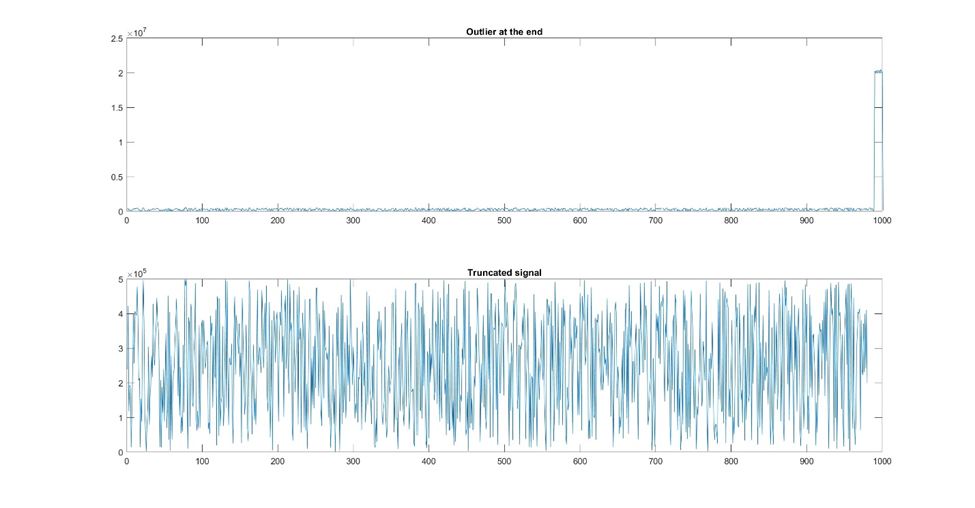
Figura 6: Às vezes, há ruído ou valores discrepantes na frente ou no final do sinal e você pode resolver isso truncando o conjunto de dados.

Como alternativa, os outliers podem ser tratados separadamente na análise, dependendo de sua importância e impacto nos resultados gerais.

Em última análise, sua abordagem ao ruído e aos outliers dependerá de seu conjunto de dados específico.

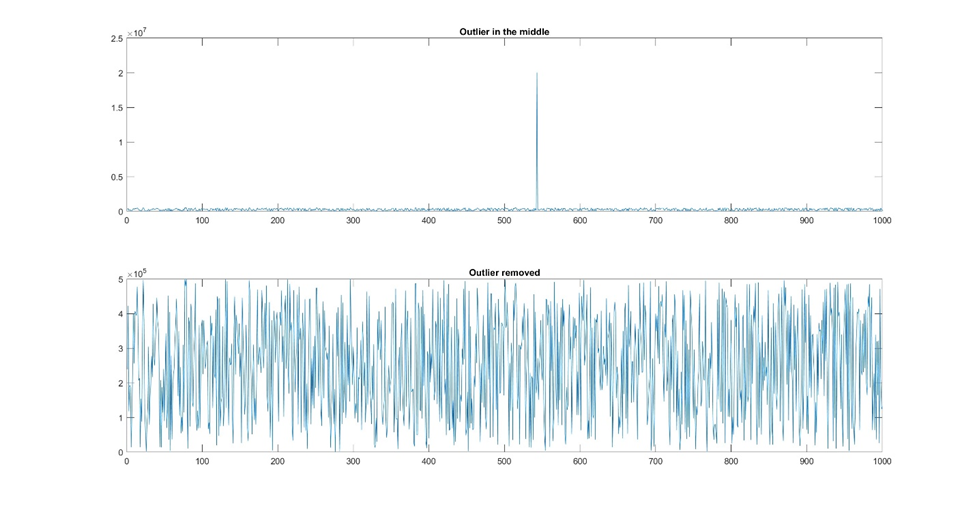
Figura 7: Se houver apenas alguns valores discrepantes, você poderá removê-los manualmente. Como alternativa, você poderia remover qualquer valor fora de uma determinada faixa de amplitude.

Uma abordagem para lidar com o ruído é a suavização para reduzir o impacto das flutuações aleatórias.

Essa técnica ajuda a revelar tendências de longo prazo e a suprimir o ruído de curto prazo. A suavização muitas vezes pode ser mais uma arte, pois é importante suavizar os dados o suficiente para reduzir o ruído de fundo sem suavizar tanto a ponto de remover o sinal também. Como a filtragem é uma etapa crucial, vamos discuti-la mais detalhadamente mais adiante.

Janelas de rolagem e médias móveis

As médias móveis e as janelas móveis são técnicas de filtragem simples, mas eficazes, usadas para suavizar dados de séries temporais e reduzir o impacto do ruído. As janelas móveis envolvem o cálculo de uma estatística específica (por exemplo, média ou desvio padrão) em uma janela móvel de pontos de dados. Essa abordagem ajuda a capturar padrões e variações localizadas nos dados.

A média móvel é uma das aplicações mais comuns das janelas móveis, em que a estatística que está sendo calculada é a média. Isso suaviza as flutuações de curto prazo, facilitando a identificação de tendências e padrões de longo prazo. As médias móveis são particularmente úteis na análise de dados financeiros, onde são empregadas para estudar as tendências de preços ao longo do tempo.

Figura 8: Um exemplo de como uma média móvel pode ser usada para suavizar um sinal. Essa média móvel foi obtida com um tamanho de janela de 3, o que significa que cada ponto de dados no gráfico da direita é uma média de três pontos de dados correspondentes no gráfico da esquerda.

Filtros passa-baixa, passa-alta e passa-banda

Os filtros passa-baixa, passa-alta e passa-banda são técnicas de filtragem baseadas em frequência usadas para passar ou bloquear determinados componentes de frequência de um sinal.

Um filtro passa-baixa permite a passagem de sinais de baixa frequência enquanto atenua os componentes de frequência mais alta, o que o torna útil para remover ruídos e reter tendências de mudanças lentas.

Por outro lado, um filtro passa-altas permite a passagem de sinais de frequência mais alta, filtrando os componentes de baixa frequência. Os filtros passa-altas são frequentemente empregados para destacar eventos de curta duração ou mudanças repentinas na série temporal.

Um filtro passa-banda permite a passagem de sinais dentro de uma faixa de frequência específica e bloqueia outros. Esse tipo de filtro é útil em aplicações em que faixas de frequência específicas contêm informações relevantes. Por exemplo, no processamento de áudio, um filtro passa-banda pode ser usado para extrair determinadas frequências correspondentes à fala humana.

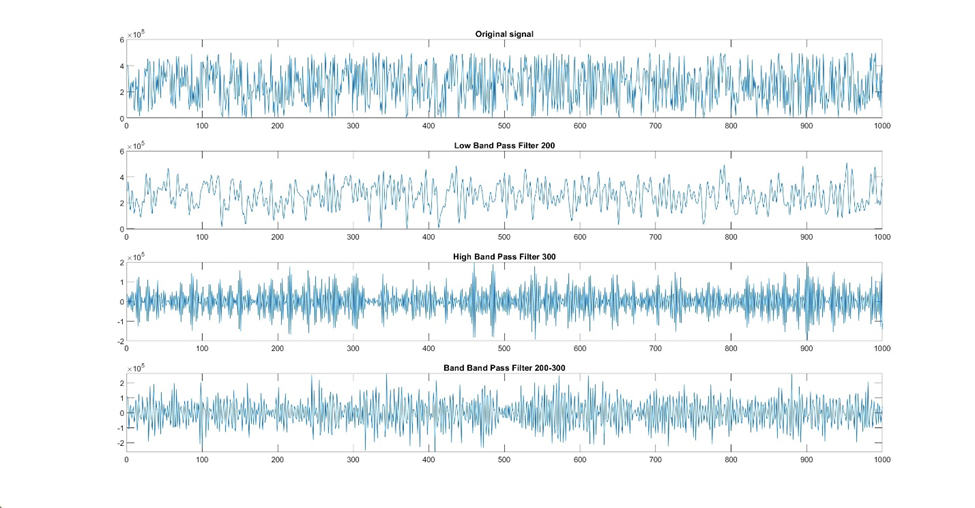
Figura 9: Uma demonstração de como diferentes tipos de filtros afetam um sinal.

Outros filtros e técnicas de suavização

A escolha do filtro ou da técnica de suavização correta para seu conjunto de dados específico pode ser demorada.

Um bom método é começar com uma passagem de banda alta ou baixa (dependendo do que você está tentando isolar) e iterar a partir daí.

Aqui está uma lista de várias técnicas de filtragem mais complexas que você pode tentar se uma técnica mais simples não isolar suficientemente o padrão desejado:

• Regressão de processo gaussiano (documentação em Matlab e Python)
• Transformada Wavelet(Matlab, Python)
• Filtros de Kalman(Matlab, Python)
• Filtro Butterworth IIR(Matlab, Python)
• Filtro FIR Savitzky-Golay(Matlab, Python.

Análise no domínio do tempo

As duas principais formas de pensar sobre sinais são no domínio do tempo e no domínio da frequência. Vamos começar com o domínio do tempo.

A análise no domínio do tempo envolve o exame do comportamento de sinais e pontos de dados em relação ao tempo. Nesta seção, exploraremos três aspectos importantes da análise no domínio do tempo: autocorrelação e correlação cruzada, recursos no domínio do tempo (média, variância, assimetria, curtose etc.) e análise de tendências com métodos de detrendência.

Recursos no domínio do tempo: média, variância, assimetria e curtose

O cálculo de vários recursos estatísticos no domínio do tempo fornece informações valiosas sobre o comportamento de uma série temporal.

A média fornece a tendência central dos dados, dando uma ideia geral do nível dos dados.

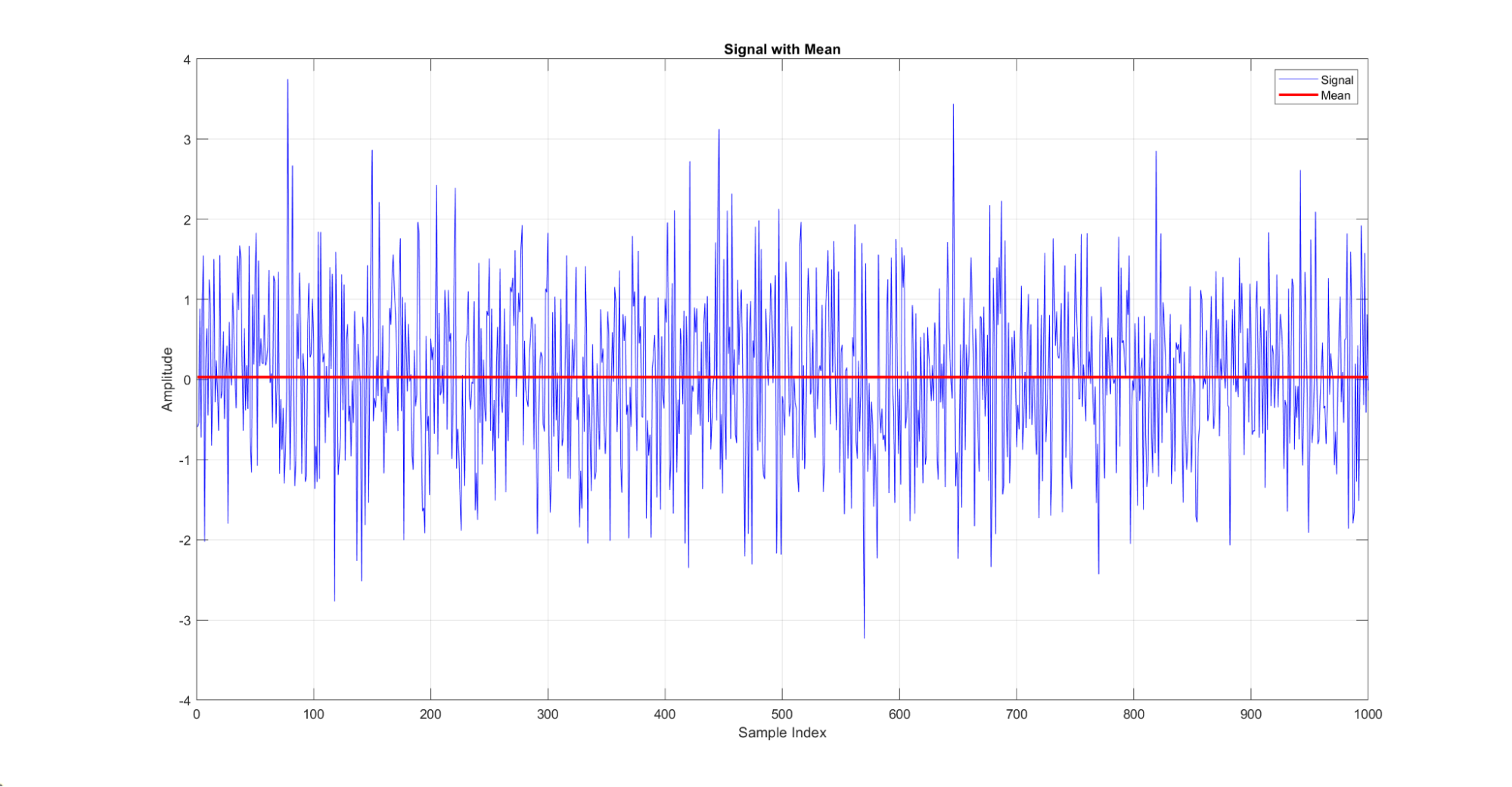
Figura 10: Uma demonstração da média de um sinal. Aqui, a linha vermelha indica a média da distribuição do sinal azul.

A variância mede a dispersão dos pontos de dados em torno da média.

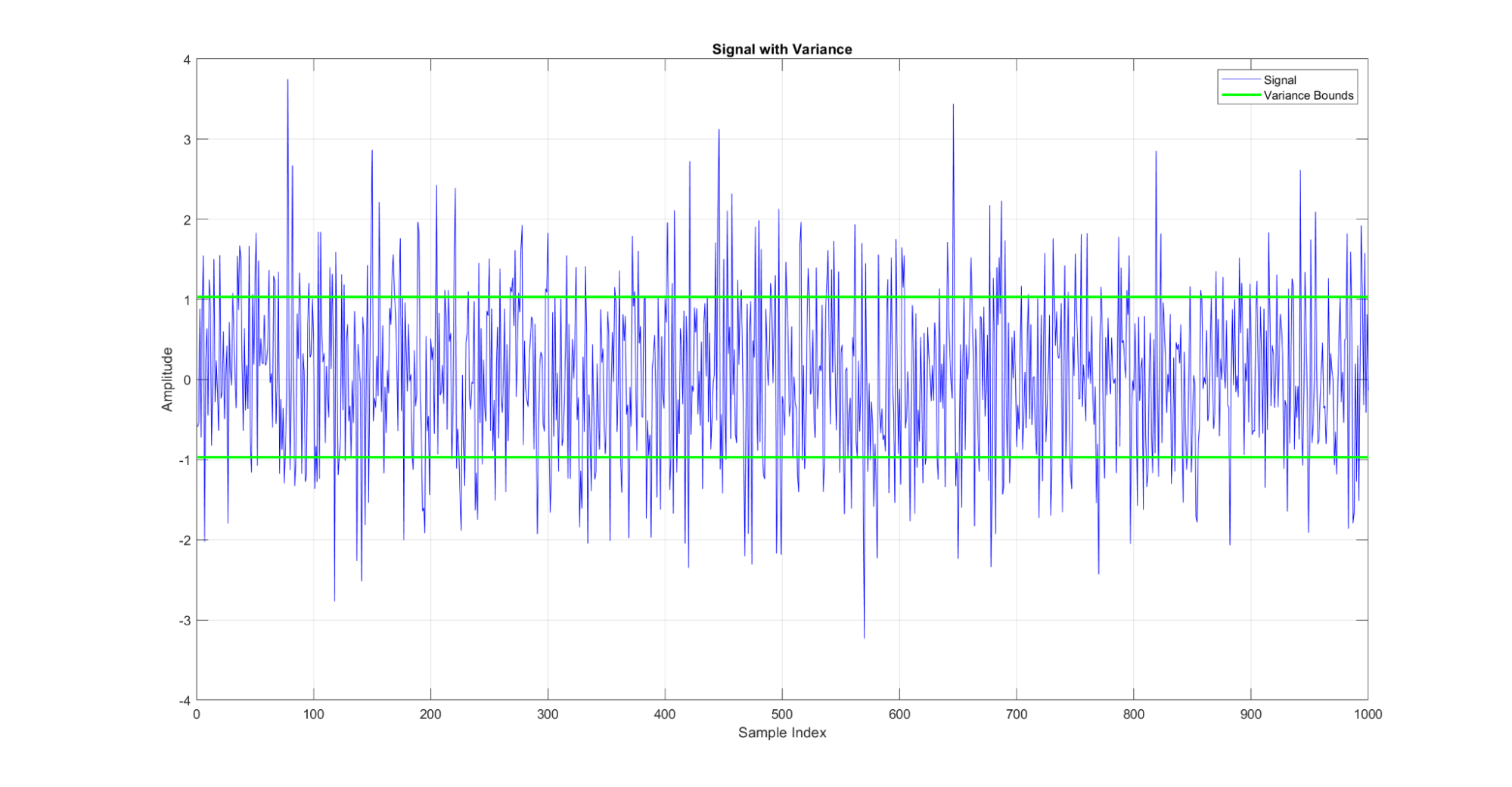
Figura 11: Uma demonstração da métrica de variância para um sinal. As linhas verdes nesse gráfico mostram a variação em torno da média do sinal.

A assimetria quantifica a assimetria da distribuição, indicando se os dados estão predominantemente espalhados em um lado.

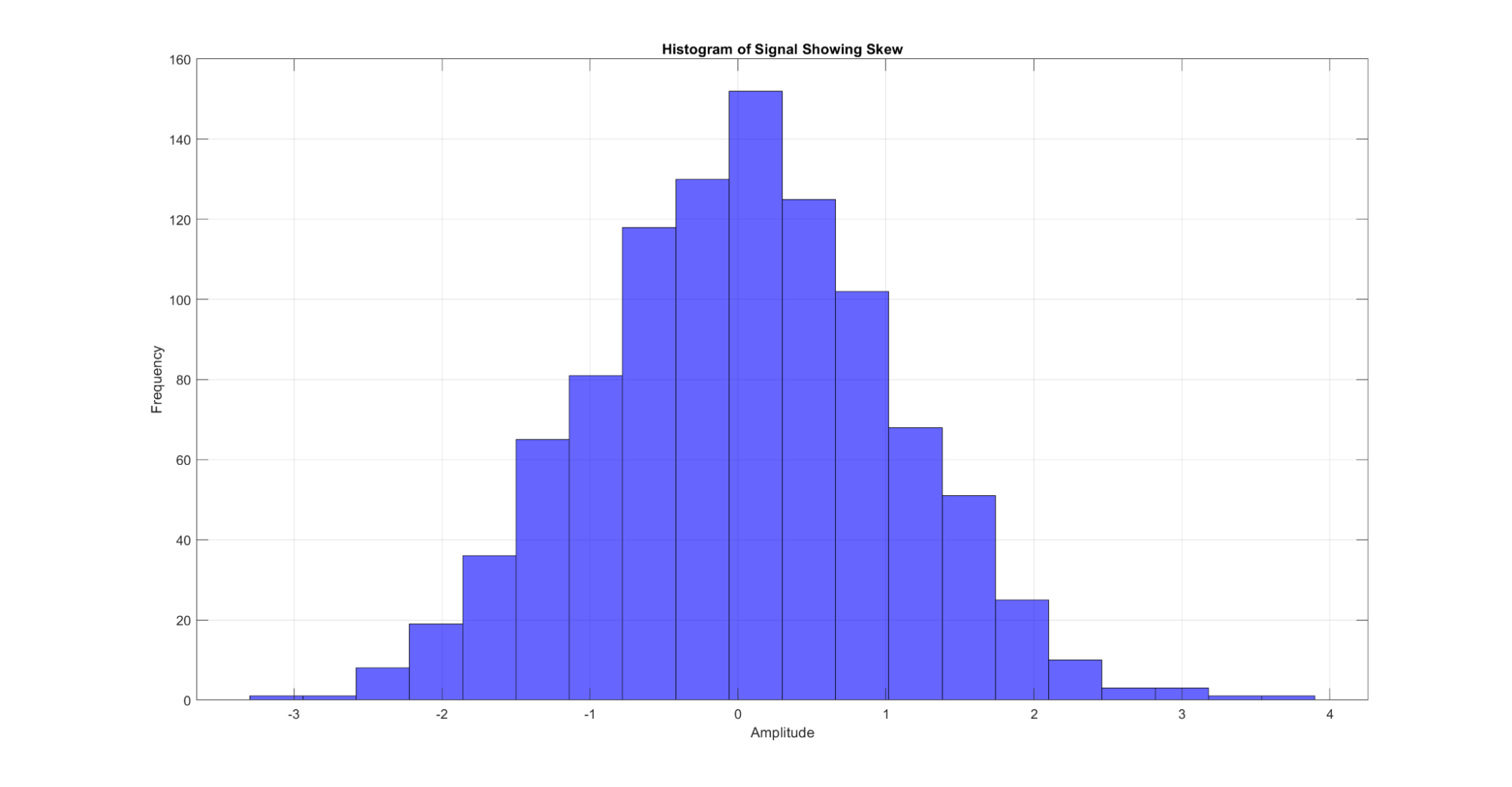
Figura 12: Uma demonstração da métrica de skew para um sinal. Quando o sinal é plotado como um histograma de frequências por amplitude, a inclinação pode ser visualizada pela assimetria nas extremidades do histograma.

A curtose mede a espessura das caudas da distribuição, caracterizando a presença de valores extremos.

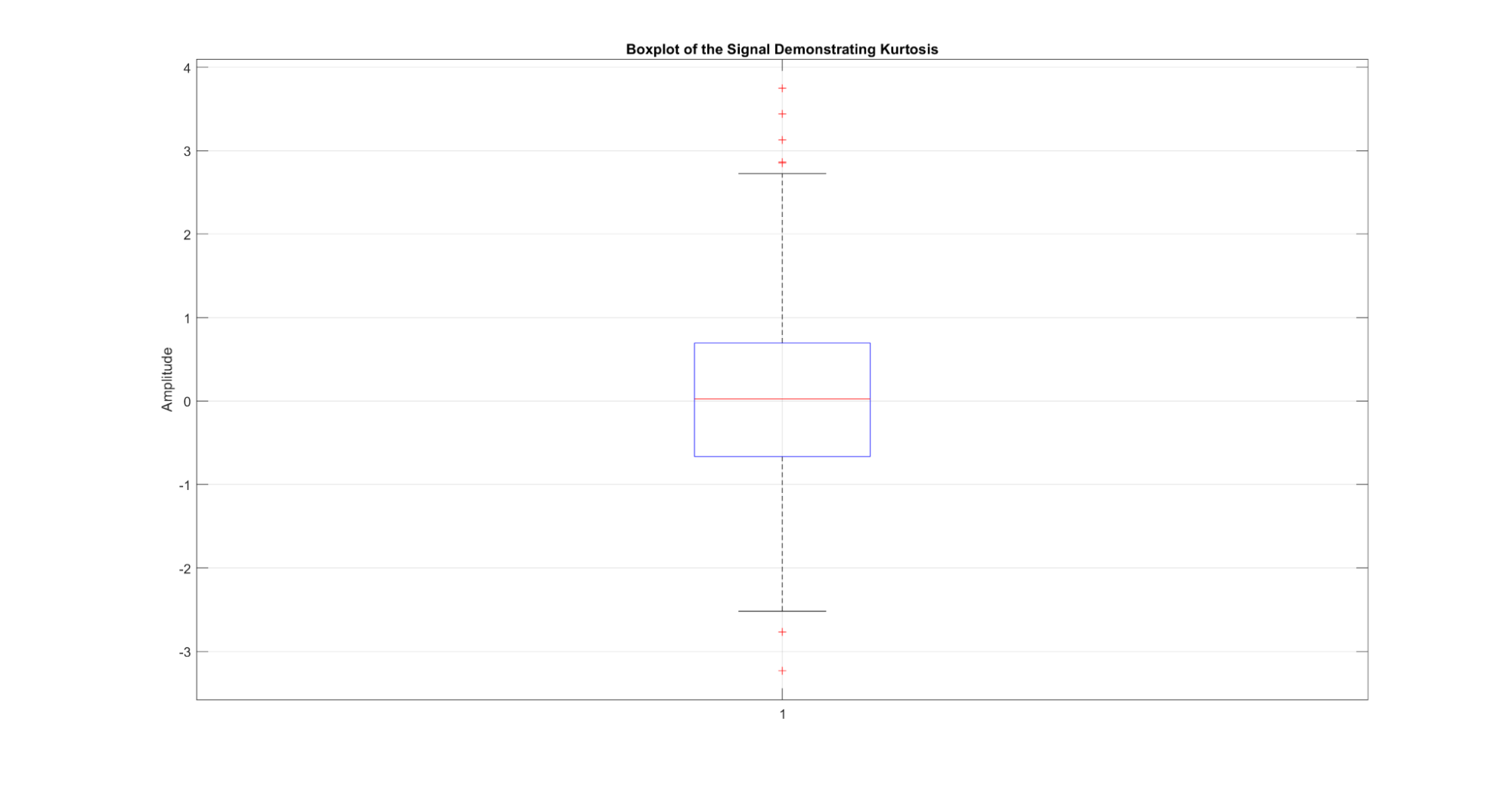
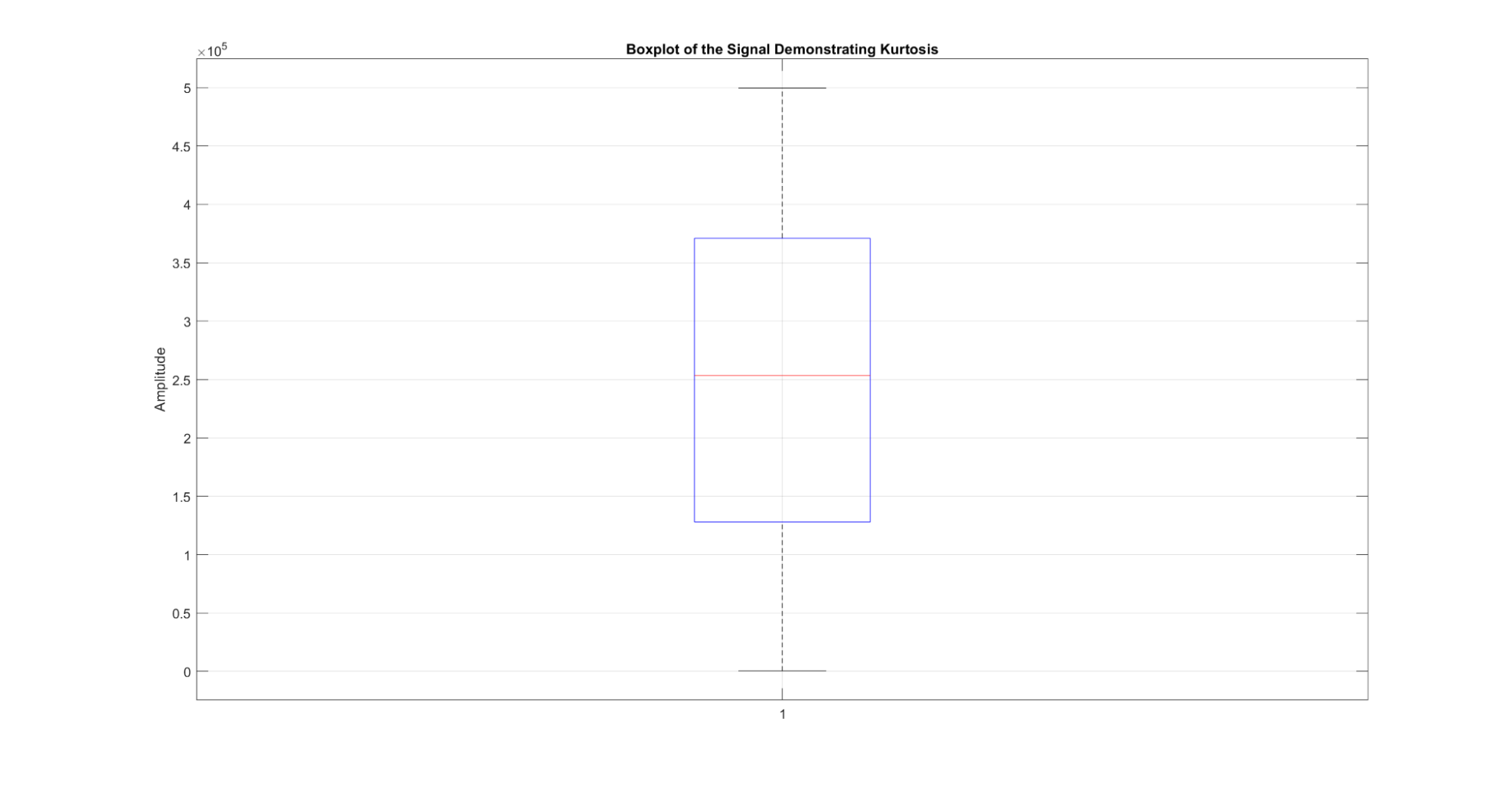
Figura 13: Uma demonstração da métrica de curtose para um sinal. Quando o sinal é plotado como um boxplot de amplitudes, a curtose pode ser visualizada pela altura da caixa.

Essas estatísticas podem parecer familiares se você já trabalhou com distribuições de dados. Essas métricas são as mesmas para dados de sinal e para distribuições.

Autocorrelação e correlação cruzada

A autocorrelação mede a similaridade entre uma série temporal e uma versão defasada dela mesma. Ele ajuda a identificar padrões repetitivos ou comportamento cíclico nos dados.

Uma forte autocorrelação em uma defasagem específica indica um padrão repetitivo com essa periodicidade. Por exemplo, em dados de infecções virais, a autocorrelação pode revelar uma sazonalidade associada a surtos.

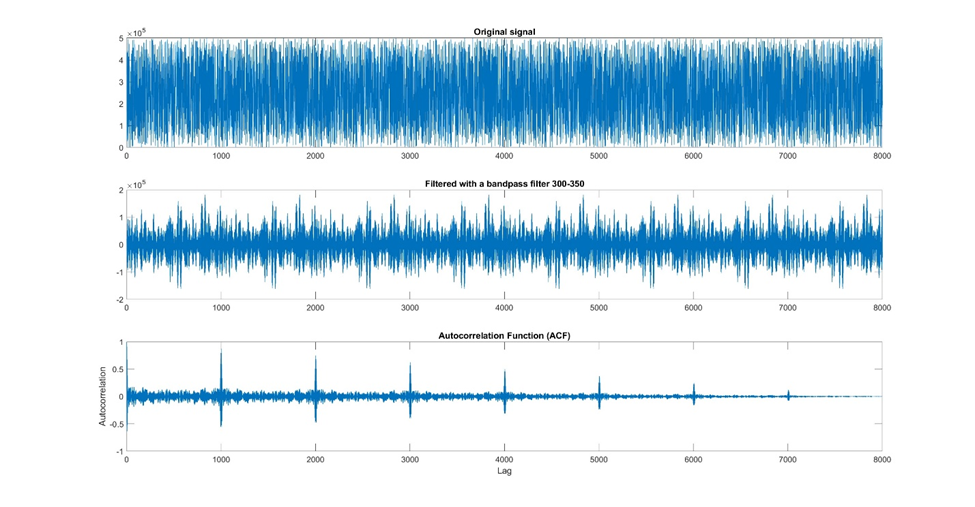
Figura 14: Um exemplo de uso da autocorrelação para identificar a periodicidade em seu sinal. Neste exemplo, peguei um sinal muito ruidoso, usei um filtro passa-banda para reduzir o ruído e, em seguida, usei uma autocorrelação para avaliar o grau de correlação do sinal com ele mesmo em diferentes defasagens de tempo. Nesse gráfico de autocorrelação, você pode ver que o sinal se repete com um período de aproximadamente 1000.

A correlação cruzada explora a relação entre dois sinais diferentes. É útil para encontrar correlações e associações defasadas entre duas variáveis. Por exemplo, a correlação cruzada pode ser usada para estudar a relação entre a temperatura e o consumo de energia ao longo do tempo.

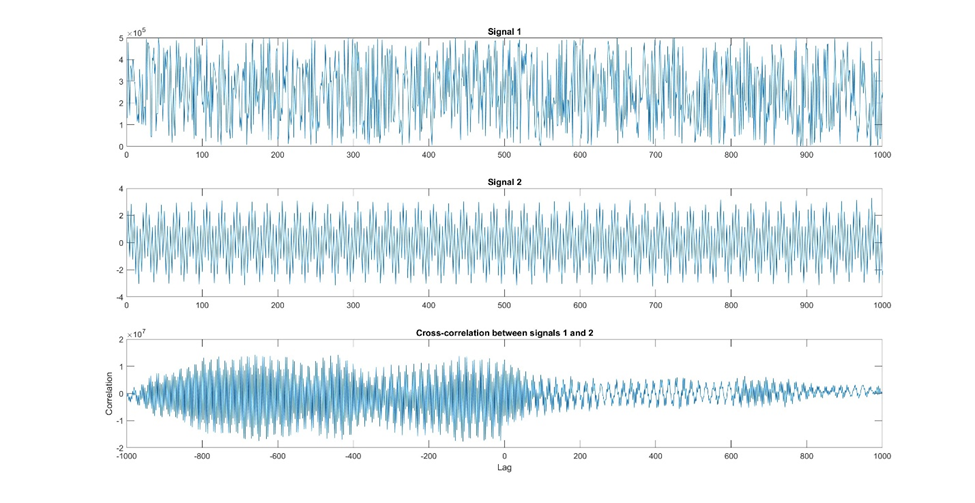
Figura 15: Aqui está um exemplo de correlação cruzada. Neste exemplo, temos dois sinais, um que pode ter alguma periodicidade e outro que tem uma periodicidade mais forte. Usando uma correlação cruzada, queremos ver se esses dois sinais estão correlacionados entre si em várias defasagens de tempo. Podemos ver no gráfico inferior que há uma correlação mais forte em defasagens negativas e quase nenhuma correlação em defasagens positivas.

Análise de tendências e métodos de detrendência

A análise de tendências é útil para entender o comportamento subjacente de longo prazo de um sinal. Uma tendência representa a direção geral na qual os dados estão se movendo durante um longo período. As tendências podem ser ascendentes (crescentes), descendentes (decrescentes) ou planas (estáveis).

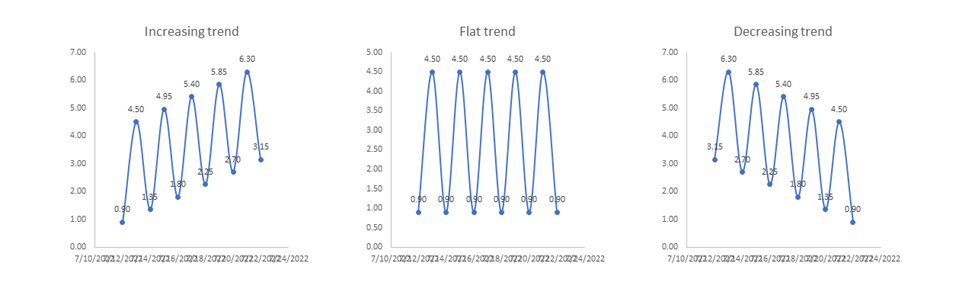
Figura 12: Exemplo de três tipos de tendências: uma tendência crescente, uma tendência plana ou estável e uma tendência decrescente.

Os métodos de detenção são aplicados para separar a tendência subjacente do sinal, o que pode ajudar a concentrar a análise nos componentes restantes, como sazonalidade e flutuações irregulares.

Um método comum de detrendência é a média móvel, em que a média de uma janela móvel é subtraída do sinal original. Outros métodos envolvem o ajuste de um polinômio ou o uso de técnicas como o filtro Hodrick-Prescott.

Em sua superfície, a detrendência parece muito com a suavização, mas as técnicas executam tarefas diferentes. A suavização reduz o ruído, o que permite que as tendências de longo prazo sejam mais claras. Por outro lado, a detrending remove as tendências de longo prazo, permitindo que a periodicidade ou a sazonalidade sejam mais óbvias. Dependendo de seus objetivos de análise, você pode usar ambos.

A visualização do sinal original junto com o sinal detrendido pode ajudá-lo a entender melhor o comportamento dos dados. Os gráficos de linha ou de haste podem exibir com eficácia tendências e dados detrendidos lado a lado.

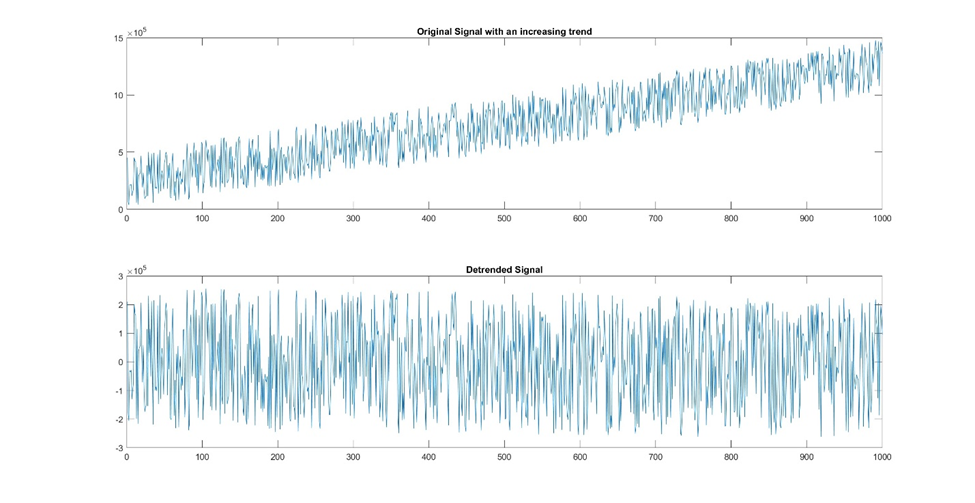
Figura 16: Esse exemplo demonstra o poder da detrendência. O sinal original tinha uma tendência de aumento positivo. Após a detrendência, o padrão resultante não mantém mais essa trajetória ascendente. Agora que a tendência foi removida, um filtro de suavização pode ser aplicado para visualizar melhor o padrão subjacente.

Análise no domínio da frequência

A análise do domínio da frequência é uma técnica poderosa que permite obter insights valiosos sobre os componentes de frequência dos dados.

Transformada de Fourier e densidade espectral de potência (PSD)

A Transformada de Fourier é uma técnica matemática usada para converter um sinal no domínio do tempo em sua representação correspondente no domínio da frequência. Ele decompõe o sinal original em uma soma de funções senoidais de diferentes frequências. O espectro de frequência resultante fornece uma imagem clara dos componentes de frequência presentes nos dados da série temporal.

A visualização do espectro de frequência geralmente é feita com um gráfico chamado PSD (Power Spectral Density, densidade espectral de potência). O gráfico PSD exibe a potência (ou magnitude ao quadrado) de cada componente de frequência. Os picos no gráfico PSD indicam as frequências dominantes nos dados, que podem revelar padrões subjacentes ou comportamento periódico.

A densidade espectral de potência é uma ferramenta fundamental na análise do domínio da frequência que mostra a distribuição da potência em relação à frequência. Ele fornece informações sobre a intensidade de diferentes componentes de frequência presentes nos dados do sinal.

Os picos altos no gráfico PSD indicam componentes de frequência fortes, enquanto os picos baixos representam os mais fracos.

Normalmente, os gráficos PSD são visualizados usando uma escala logarítmica para aumentar a visibilidade das frequências mais fracas. Esses gráficos ajudam a identificar frequências significativas que podem corresponder a padrões ou fenômenos específicos nos dados.

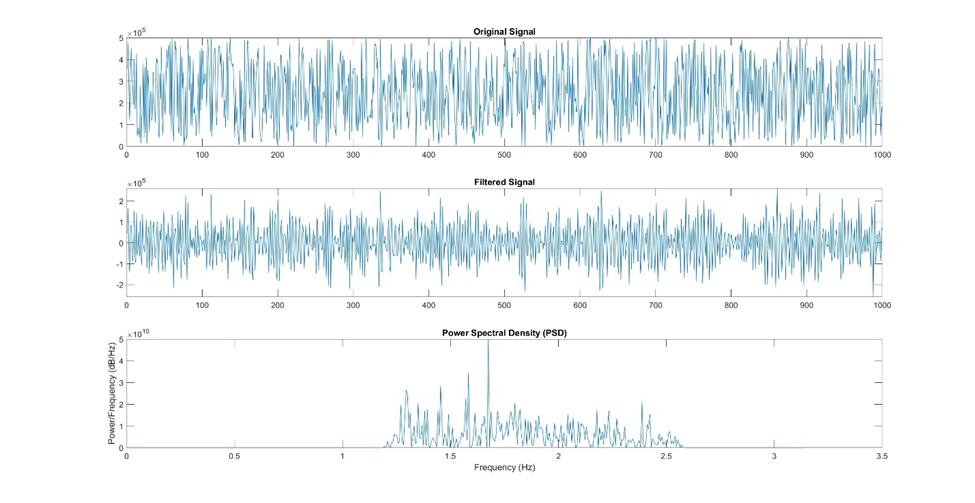
Figura 17: Aqui está um exemplo de uso de um gráfico de densidade espectral de potência (PSD) para examinar a intensidade de diferentes componentes de frequência no sinal. O sinal original foi primeiro filtrado usando um filtro passa-banda e, em seguida, um gráfico de densidade espectral de potência foi criado usando uma função integrada no Matlab.

Espectrograma e análise de tempo-frequência

O espectrograma é uma técnica de visualização valiosa usada para examinar como o conteúdo de frequência de um sinal muda ao longo do tempo. Ele fornece uma representação tempo-frequência dos dados, dividindo o sinal em pequenos segmentos e calculando a transformada de Fourier para cada segmento.

Ao usar um mapa de cores para representar a potência ou a magnitude de cada componente de frequência, o espectrograma exibe uma visão tridimensional dos dados. As regiões de cores mais quentes no espectrograma indicam componentes de frequência mais fortes em intervalos de tempo específicos, enquanto as regiões de cores mais frias sugerem frequências mais fracas ou inexistentes.

A análise de tempo-frequência ajuda a detectar eventos transitórios ou alterações nas características de frequência que não são facilmente observáveis apenas no domínio do tempo ou da frequência. Isso é particularmente útil em aplicativos como processamento de fala e áudio, em que diferentes fonemas ou sons podem ter componentes de frequência variáveis ao longo do tempo.

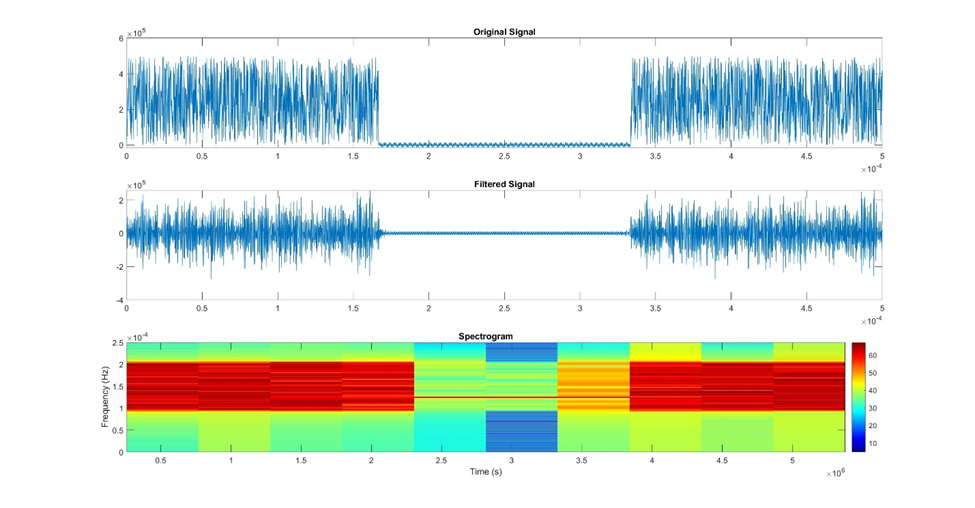
Figura 18: Este é um exemplo de como visualizar seu sinal como um espectrograma. O sinal original foi filtrado usando um filtro de banda e, em seguida, plotado como um espectrograma usando uma função padrão do Matlab.

Aplicações do processamento de sinais

As aplicações do processamento de sinais são diversas e abrangem vários campos. Vamos explorar algumas aplicações importantes do processamento de sinais na ciência de dados:

Finanças e previsão do mercado de ações

O processamento de sinais é altamente influente no setor financeiro, permitindo uma análise aprofundada dos dados financeiros de séries temporais.

Ao aplicar técnicas de filtragem, análise de tendências e recursos de domínio do tempo, os cientistas de dados podem identificar padrões, tendências e anomalias nos dados do mercado de ações.

Os modelos de previsão são utilizados para prever tendências de mercado, preços de ações e avaliações de risco. Essas previsões são fundamentais para que investidores, traders e instituições financeiras tomem decisões bem informadas e gerenciem portfólios de forma eficaz.

Para obter uma visão mais aprofundada da análise de dados financeiros, confira o catálogo de cursos de dados financeiros do DataCamp ou este curso Introdução aos conceitos financeiros em Python.

Dados de sensores da Internet das Coisas (IoT)

A Internet das Coisas (IoT) gera grandes volumes de dados de séries temporais de vários sensores e dispositivos.

O processamento de sinais ajuda a extrair informações valiosas desses dados, levando a percepções acionáveis. Ao analisar os dados do sensor de IoT, os cientistas de dados podem monitorar a integridade do equipamento, detectar anomalias e otimizar o desempenho.

Por exemplo, na manufatura inteligente, as técnicas de processamento de sinais são empregadas para prever falhas nas máquinas e evitar o tempo de inatividade, aumentando a produtividade e reduzindo os custos de manutenção.

O DataCamp tem um ótimo curso sobre análise de dados de IoT. Dê uma olhada!

Processamento de sinais biomédicos e de saúde

O processamento de sinais é usado em aplicações biomédicas e de saúde, em que o monitoramento contínuo de sinais fisiológicos é vital para o atendimento ao paciente.

Por exemplo, em eletrocardiogramas (ECGs) e eletroencefalogramas (EEGs), as técnicas de processamento de sinais ajudam a detectar anormalidades, avaliar as condições do paciente e auxiliar no diagnóstico e no planejamento do tratamento.

Além disso, a análise no domínio do tempo e no domínio da frequência ajuda a descobrir padrões ocultos em sinais médicos, levando a avanços na detecção de doenças e na compreensão da fisiologia humana.

Além das aplicações na área da saúde, o processamento de sinais é amplamente utilizado na pesquisa biomédica. É útil na análise de dados genômicos e outros sinais biológicos, fornecendo informações valiosas sobre mecanismos de doenças, descoberta de medicamentos e medicina personalizada.

Confira este curso do DataCamp sobre análise de imagens biomédicas em Python que usa algumas dessas técnicas.

Processamento de fala e áudio

No processamento de fala e áudio, as técnicas de processamento de sinais são empregadas para analisar e interpretar a linguagem falada e os sinais de áudio.

Os sistemas de reconhecimento automático de fala (ASR), assistentes de voz e reconhecimento de emoção de fala dependem de algoritmos de processamento de sinais para extrair recursos relevantes e reconhecer padrões de fala.

Os aplicativos de processamento de áudio, como redução de ruído, aprimoramento de áudio e síntese de fala, também aproveitam bastante os métodos de processamento de sinais.

Se você estiver interessado em saber mais, o DataCamp tem um excelente curso sobre Processamento de linguagem falada em Python.

Processamento de imagens e vídeos

O processamento de sinais é usado até mesmo na análise de imagens e vídeos, permitindo aplicações como reconhecimento de imagens, detecção de objetos e vigilância por vídeo.

Técnicas como a Transformada de Fourier são usadas para compactação de imagens e extração de recursos. As análises de tempo-frequência, como os espectrogramas, desempenham um papel fundamental na sincronização de sinais de vídeo e áudio, permitindo tecnologias de leitura labial e reconhecimento de gestos.

Para obter mais informações sobre processamento de imagens, recomendo este curso de processamento de imagens no DataCamp.

Análise de dados do sensor

O processamento de sinais está no centro da análise de dados de sensores, que é usada em áreas como monitoramento ambiental, previsão do tempo e automação industrial. Ele ajuda a identificar padrões e tendências nos dados do sensor, permitindo a manutenção preditiva, a detecção de anomalias e a otimização de sistemas e processos.

Aplicações científicas e de pesquisa

O processamento de sinais é usado em muitos estudos científicos para examinar tudo, desde sinais de pressão a tremores sísmicos e tensões. Essas técnicas foram usadas até mesmo para identificar os sons emitidos pelas asas dos beija-flores!

Práticas recomendadas e dicas para processamento de sinais em ciência de dados

O processamento de sinais é uma metodologia poderosa, mas, para produzir resultados precisos e significativos, requer a adesão a práticas recomendadas e considerações cuidadosas. Aqui estão algumas dicas essenciais para garantir o sucesso do processamento de sinais.

Pré-processamento e limpeza de dados

Antes de mergulhar nas técnicas de processamento de sinais, é fundamental realizar um pré-processamento e uma limpeza completos dos dados! Isso envolve o manuseio de valores ausentes, o tratamento de valores discrepantes e a normalização dos dados para garantir a consistência e a confiabilidade. As técnicas de redução de ruído, como a filtragem, são úteis para remover distúrbios indesejados que podem afetar a análise do sinal.

Visualizações para insight

As visualizações são uma ferramenta superpoderosa no processamento de sinais. Eles fornecem uma compreensão clara dos padrões de dados e da eficácia das técnicas aplicadas.

É altamente recomendável que você visualize seus dados em cada etapa do pré-processamento e da análise.

Gráficos no domínio do tempo, espectros de frequência e espectrogramas são visualizações comuns para sinais.

Escolha das técnicas corretas de processamento de sinais para problemas específicos

O processamento de sinais inclui uma ampla variedade de técnicas, cada uma adaptada a tipos específicos de dados e problemas. Compreender a natureza dos dados e os objetivos da análise é essencial para selecionar as técnicas adequadas. Para dados de séries temporais, técnicas como a Transformada de Fourier e a autocorrelação são úteis para a análise de frequência e padrão. Os dados de imagem exigem técnicas de processamento de imagem, como detecção de bordas e extração de recursos.

Conclusão

O processamento de sinais é um componente fundamental da ciência de dados, capacitando os profissionais a extrair insights valiosos de dados complexos em vários setores. De finanças a saúde, de fala a processamento de imagens, a análise de sinais desempenha um papel importante na transformação de dados brutos em percepções acionáveis.

Os recentes avanços no aprendizado de máquina e nos recursos computacionais impulsionaram o desenvolvimento de técnicas inovadoras de processamento de sinais. Confira como usar o aprendizado de máquina com seus dados de sinal em um artigo separado.

A primeira vez que você recebe a tarefa de processar dados de sinal pode ser assustadora. Esperamos que este tutorial tenha lhe dado as ferramentas para isolar um padrão de voz, detectar um terremoto ou prever um aumento no preço das ações.

Se este artigo o interessou, o DataCamp tem vários code-alongs que você pode querer conferir. Aqui está um para Análise de tempo em Python e um estudo de caso Analisando uma série temporal do rio Tâmisa em Python. Há também tutoriais sobre séries temporais em Python e planilhas eletrônicas.