Course
R is one of the main languages used for data science today. As such, it is natural that any beginner may want to know how to get started with this powerful language regardless of the operating system running on a computer. Thus, this tutorial will address this by covering the installation process of R on Windows 10, Mac OSX, and Ubuntu Linux.
Furthermore, it will also go over the installation of RStudio, which is an IDE (Integrated Development Environment) that makes R easier to use as well as how to install R packages such as dplyr or ggplot2.
Installing R on Windows 10
Installing R on Windows 10 is very straightforward. The easiest way is to install it through CRAN, which stands for The Comprehensive R Archive Network. Just visit the CRAN downloads page and follow the links as shown in the video below:
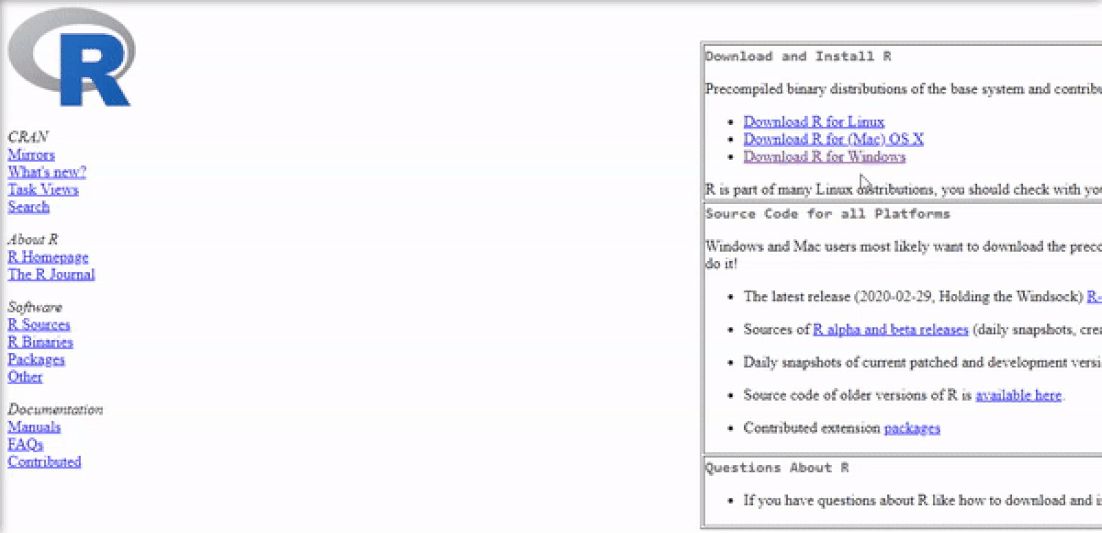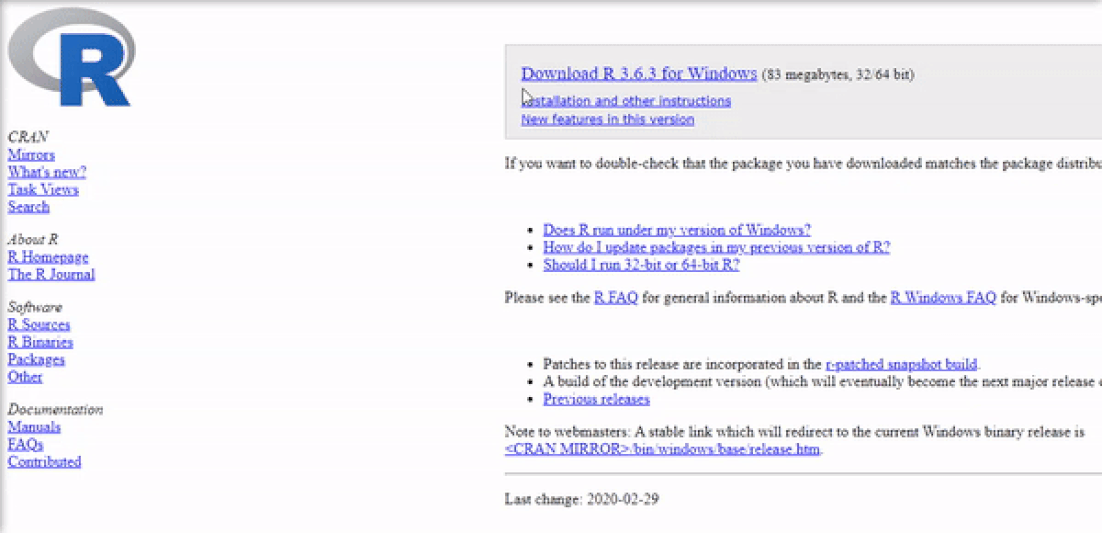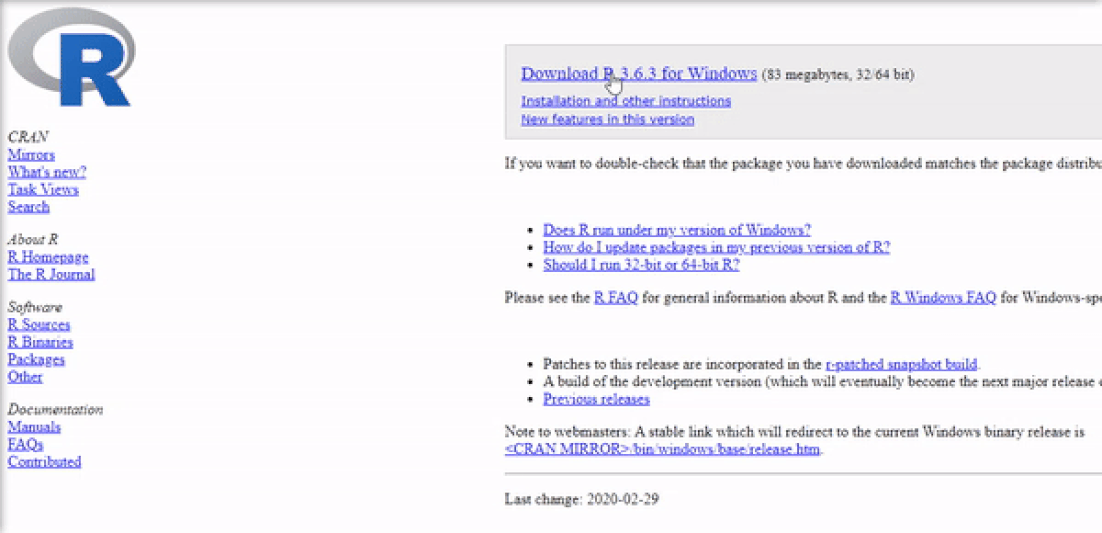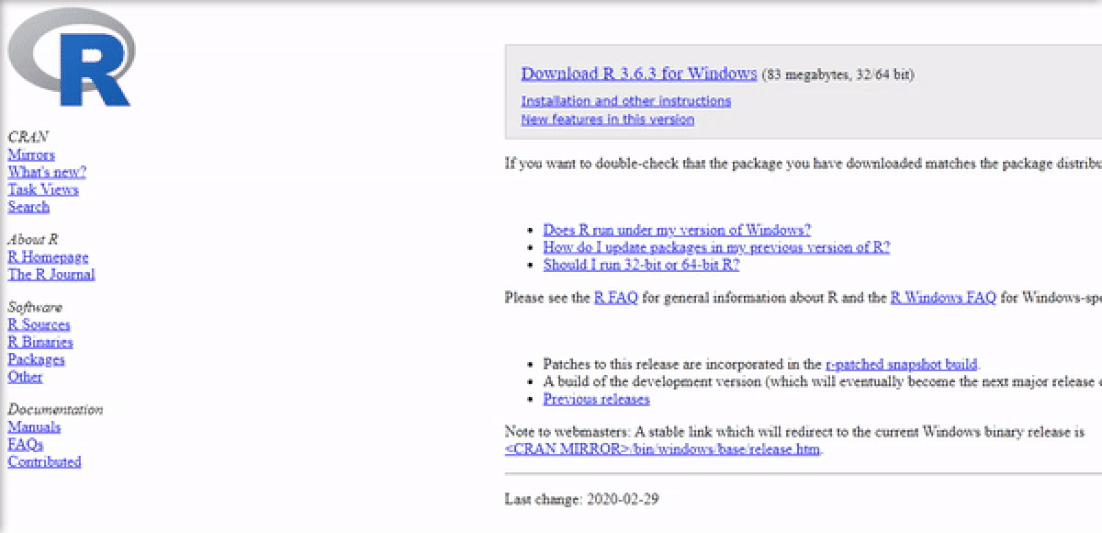
Once the download is finished, you will obtain a file named "R-3.6.3-win.exe" or similar depending on the version of R that you download. The links shown in the video above will take you to the most recent version. To finish installing R on your computer, all that is left to do is to run the .exe file. Most of the time, you will likely want to go with the defaults, so click the button 'Next' until the process is complete, as shown in the video below. Note that, even though I do not do so, you can add desktop or quick start shortcuts during the process.

Installing RStudio
Once R is installed, you can proceed to install the RStudio IDE to have a much-improved environment to work in your R scripts. It includes a console that supports direct code execution and tools for plotting and keeping track of your variables in the workspace, among other features. The installation process is very straightforward, as well. Simply go to the RStudio downloads page and follow the video below:
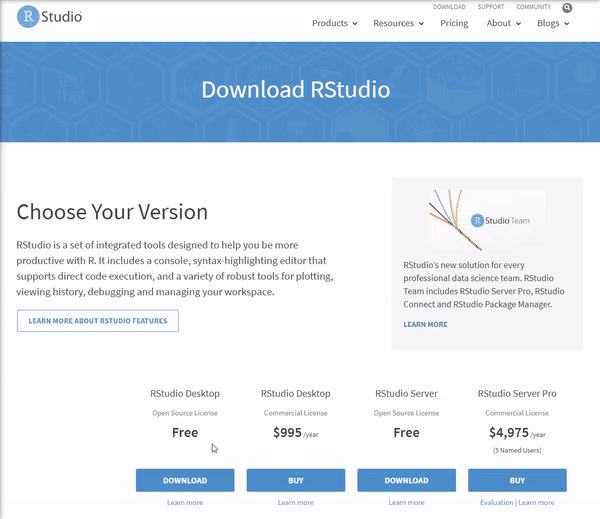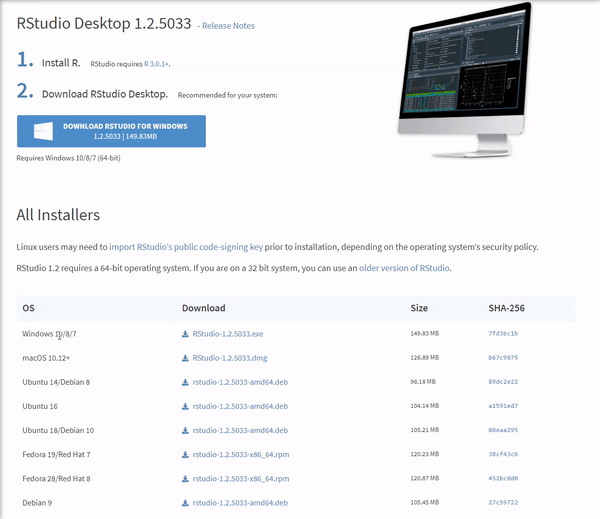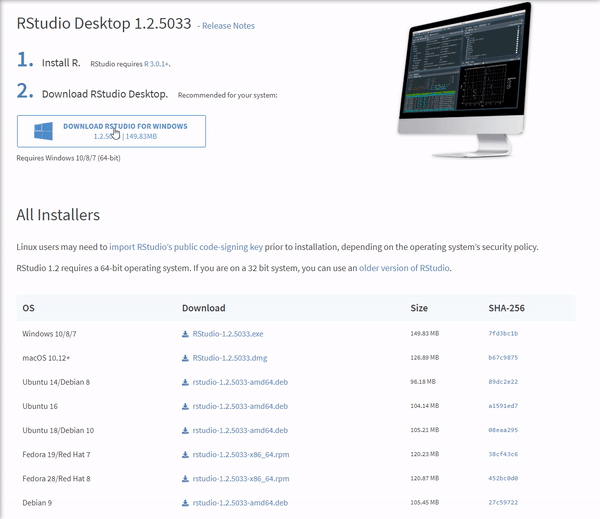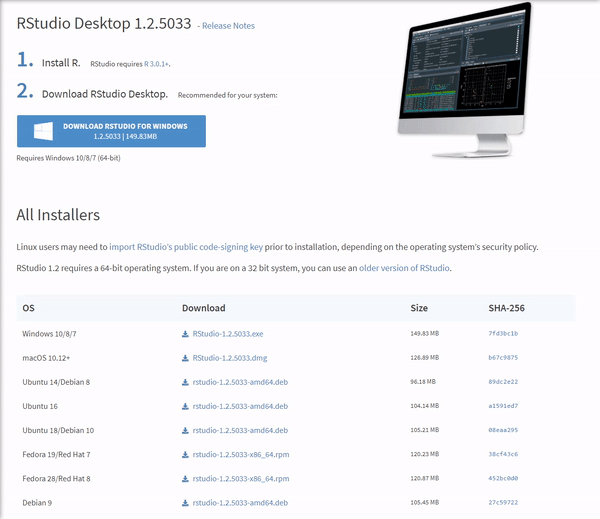
Once the download is complete, you will get a file named "RStudio-1.2.5033.exe" or similar. Again this will be dependent on the version. To complete the installation, it is as easy as before. Just run the previously mentioned .exe file with the default settings by clicking 'Next', and wait until the installation finishes. Bear in mind that RStudio requires that R is installed beforehand.
Installing Packages in R
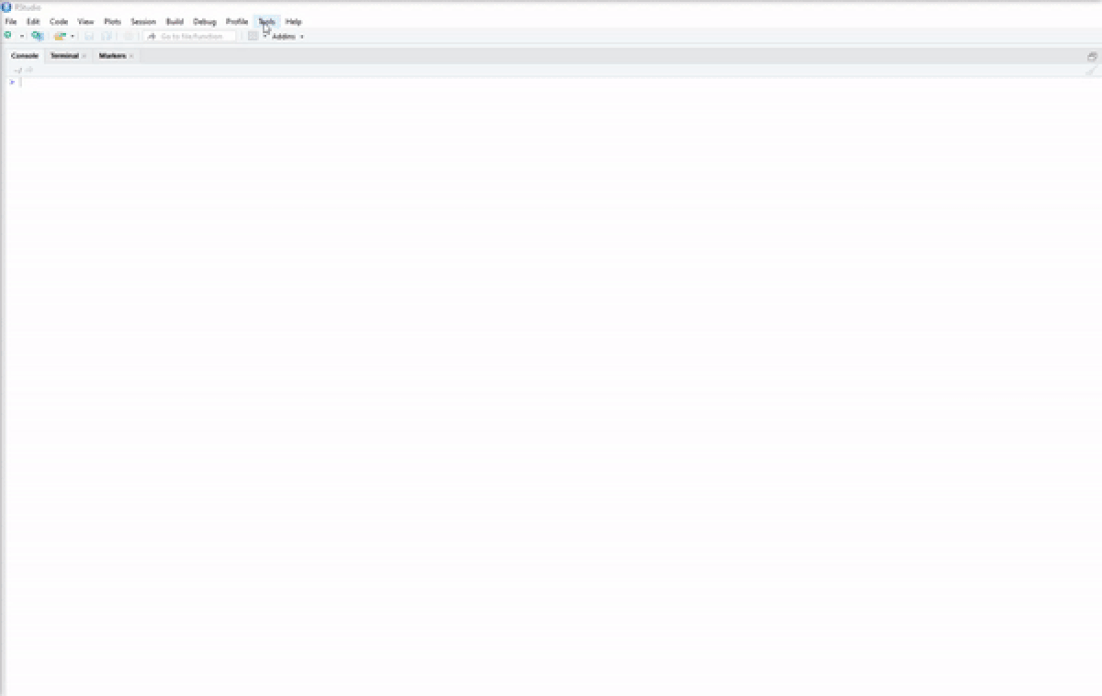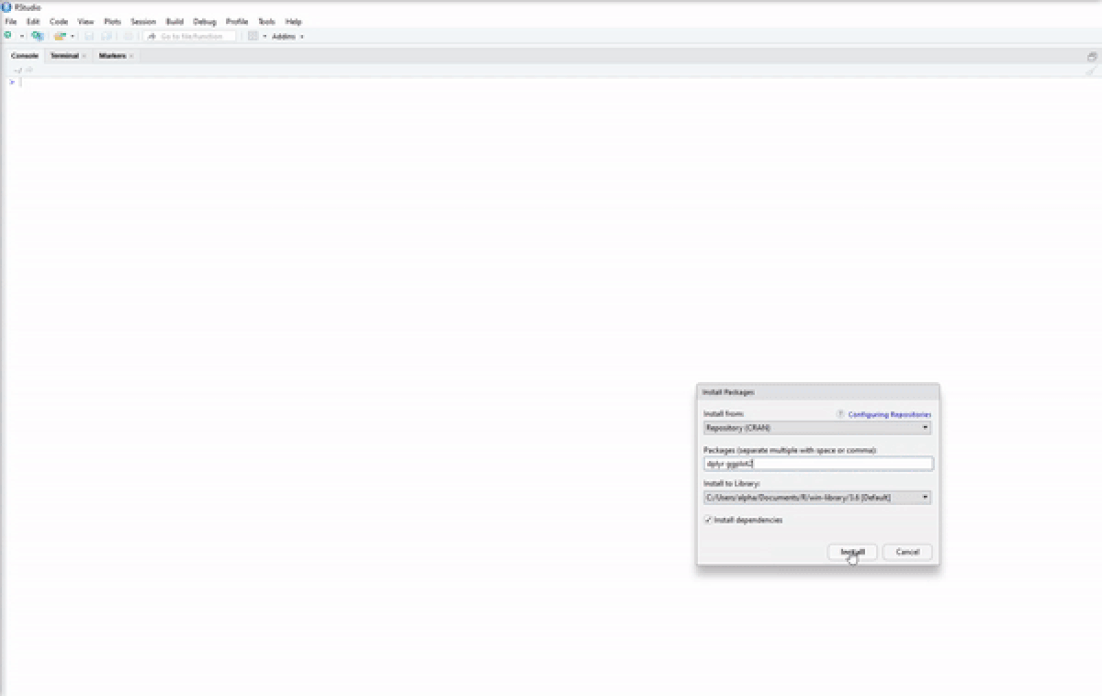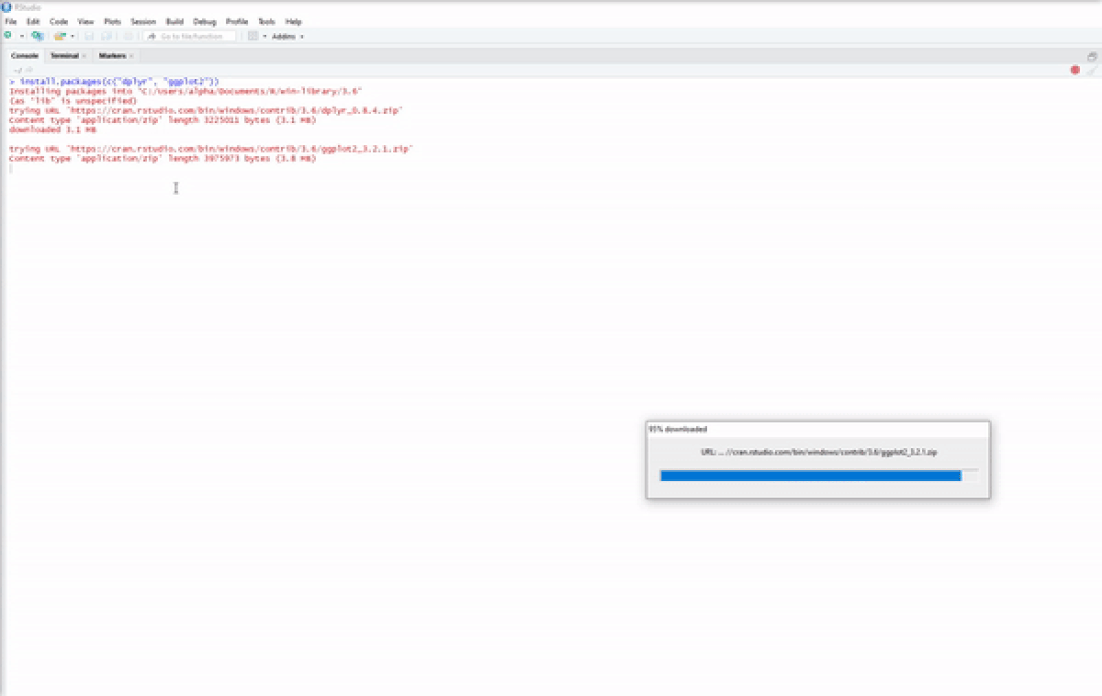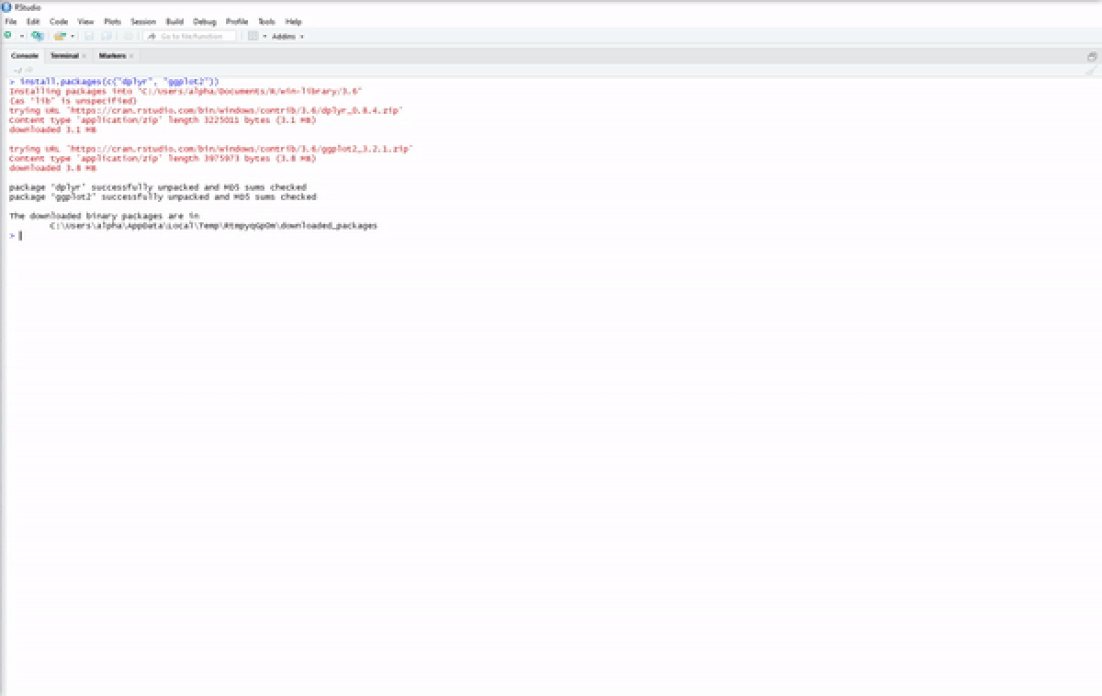
Now you have base R installed on your system and a nice IDE to begin your R programming journey. However, base R is rather limited in the things that it can do, which is why we have R packages such as dplyr for enhanced data-wrangling capabilities or ggplot2 for improved data visualizations. There are two simple ways to install R packages using RStudio. The first is to execute the following line of code in the console:
install.packages(c("dplyr","ggplot2"))
The second is shown in the video below. It is an easy-to-use graphical interface built into RStudio from which you can search and download any R package available on CRAN.
Installing R on Mac OSX
Installing R on Mac OS is similar to Windows. Once again, The easiest way is to install it through CRAN by going to the CRAN downloads page and following the links as shown in the video below:
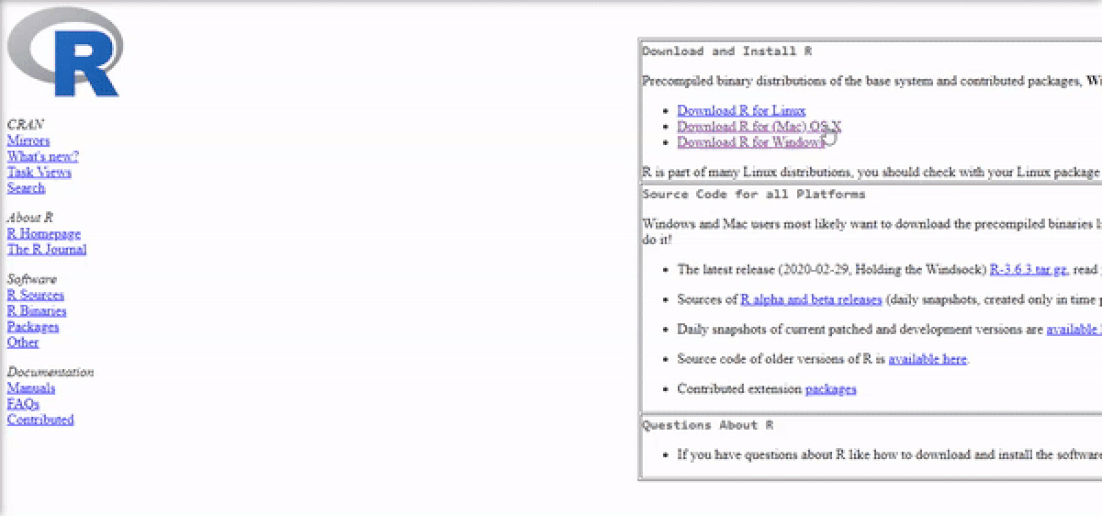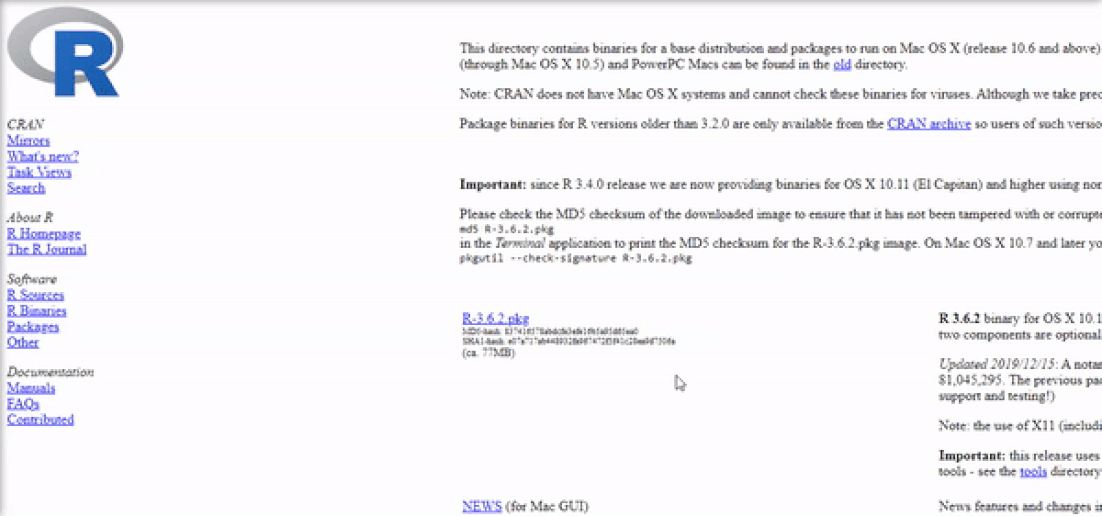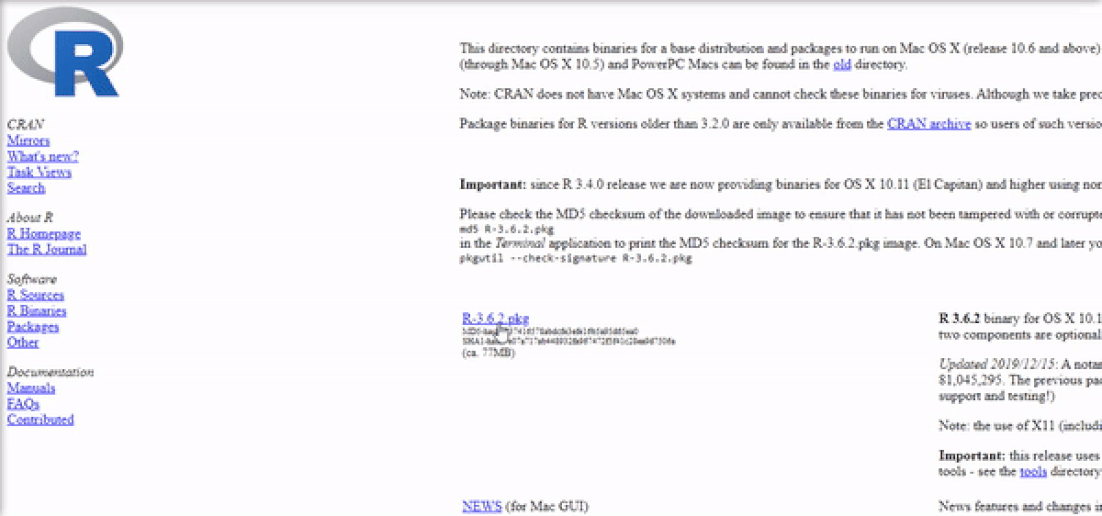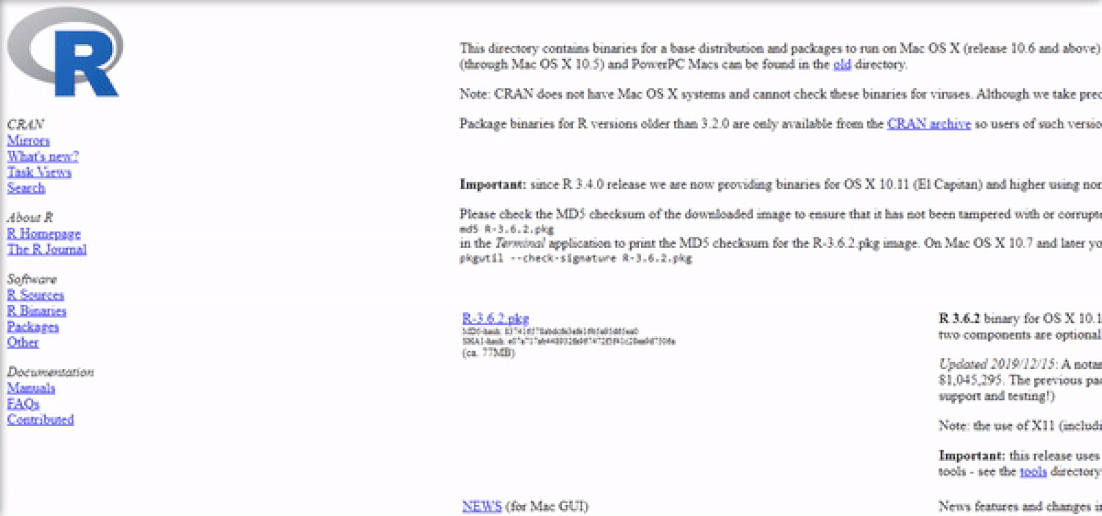
The next step is to click on the "R-3.6.2.pkg" (or newer version) file to begin the installation. You can leave the default options as is just like for Windows.
Installing RStudio and R packages
This process is essentially the same as in Windows. To download RStudio, go to the RStudio downloads page and get the .dmg for Mac OS, as shown in the image below. Remember to keep default installation options.

Once you open RStudio, installing packages is the same as with Windows. You can use either install.packages(c("dplyr","ggplot2")) in the console or go ahead and use the graphical interface shown in the video under the installing packages in R subsection of this tutorial.
Installing R on Ubuntu 19.04/18.04/16.04
Installing R on Ubuntu maybe a little bit more tricky for those unused to working in the command line. However, it is perhaps just as easy as with Windows or Mac OS. Before you start, make sure to have root access in order to use sudo.
As it is common, prior to installing R, let us update the system package index and upgrade all our installed packages using the following two commands:
sudo apt update
sudo apt -y upgrade
After that, all that you have to do is run the following in the command line to install base R.
sudo apt -y install r-base
Installing RStudio and R Packages
Once base R is installed, you can go ahead and install RStudio. For that we are going to head over again to the RStudio downloads page and download the .deb file for our Ubuntu version as shown in the image below:
Once you have the .deb file, all that is left is to navigate to your downloads folder using cd Downloads in the command line and then run the following command to begin the installation process:
sudo dpkg -i rstudio-1.2.5033-amd64.deb
You may encounter some dependency problems that may cause your first try to install RStudio to fail, but this has an easy fix. Just run the following command and try again:
sudo apt -f install
When the process finishes, you will have an RStudio shortcut in your Ubuntu app list, but you will also be able to start RStudio by typing rstudio in the command line.
Once you open RStudio, installing packages can be done in the exact same manner as with Windows or Mac OS. Either by typing install.packages(c("dplyr","ggplot2")) in the console or using the graphical interface shown in the video under the installing packages in R subsection of this tutorial
Conclusion
I hope that this tutorial will help those of you eager to dive into the world of R programming regardless of your operating system choice. If you are looking to start learning R as such after installing it, please refer to the Introduction to R course, which will guide you through the basics of R programming. Keep learning; the sky is the limit.
Check out the following DataCamp tracks:
