Charakteristische Gleichung: Alles, was du für Data Science wissen musst

Mit der exponentiellen Zunahme der Verfügbarkeit von Daten und maschinellen Lernverfahren hat die lineare Algebra einen grundlegenden Platz in der Mathematik des maschinellen Lernens und der Datenwissenschaft gefunden. Daher werden angehende Wissenschaftler/innen für maschinelles Lernen und Datenwissenschaftler/innen sehr davon profitieren, grundlegende Konzepte der linearen Algebra zu erlernen, einschließlich Vektoren und Matrizen, deren Eigenschaften und gängige Operationen, die auf sie angewendet werden.

Ich empfehle dir, unseren Kurs Lineare Algebra für Data Science in R zu belegen, um eine solide mathematische Grundlage für Data Science und maschinelles Lernen zu entwickeln. Wenn du den Kurs belegst, wirst du die lineare Algebra als ein schönes und interessantes Fach schätzen lernen, das die Synthese von Algebra und Geometrie (durch Linien, Ebenen und Volumen) beinhaltet. Insbesondere wirst du sehen, dass sich hochdimensionale Daten gut für die Darstellung in Form von Vektorobjekten eignen (z. B. Text, Bilder, Audio und Funktionen) und dass diese mathematischen Objekte als Vektoren umfangreiche Anwendungen in Wissenschaft und Technik haben, z. B. in der Physik, Statistik und Informatik.

In diesem Artikel werden wir uns eines der grundlegenden Objekte der linearen Algebra, die Matrix, genauer ansehen. Wie andere mathematische Objekte haben auch Matrizen einige Eigenschaften, die sie charakterisieren. Auf werde ich insbesondere eine charakteristische Eigenschaft einer quadratischen Matrix vorstellen: das charakteristische Polynom oder die charakteristische Gleichung. Schauen wir uns das mal an.

Definition der charakteristischen Gleichung

Ein Polynom ist eine Funktion mit Unbekannten der Potenz n. Die Unbekannte wird in der Regel durch den Buchstaben x dargestellt, aber in besonderen Anwendungsfällen wird eine andere Schreibweise verwendet, wie zum Beispiel der griechische Buchstabe 𝝀 (lambda), den wir in unserer Notation verwenden werden. Das charakteristische Polynom einer quadratischen Matrix A ∈Rn× n und der Unbekannten 𝝀 ist definiert als:

Dabei ist det(.) die Determinante einer quadratischen Matrix und I ist die Identitätsmatrix.

Wenn wir dieses charakteristische Polynom gleich Null setzen (um zu lösen 𝝀), nennen wir es die charakteristische Gleichung. Die Wurzeln dieser Polynomgleichung werden als Eigenwerte bezeichnet. Sie sind wichtige Konzepte bei der Matrixtransformation und beim maschinellen Lernen (z. B. bei der Dimensionalitätsreduktion). Wenn du dir über Eigenvektoren und Eigenwerte unsicher bist, findest du hier ein Tutorial zu diesem Thema: Eigenvektoren und Eigenwerte: Wichtige Einblicke für Data Science.

Ableiten und Berechnen der charakteristischen Gleichung

Wir zeigen, wie man ein charakteristisches Polynom für eine 2x2 quadratische Matrix A formuliert, wobei:

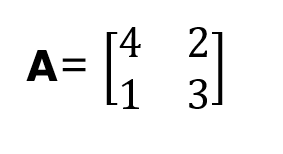
Aus der Definition eines charakteristischen Polynoms ergibt sich, dass:

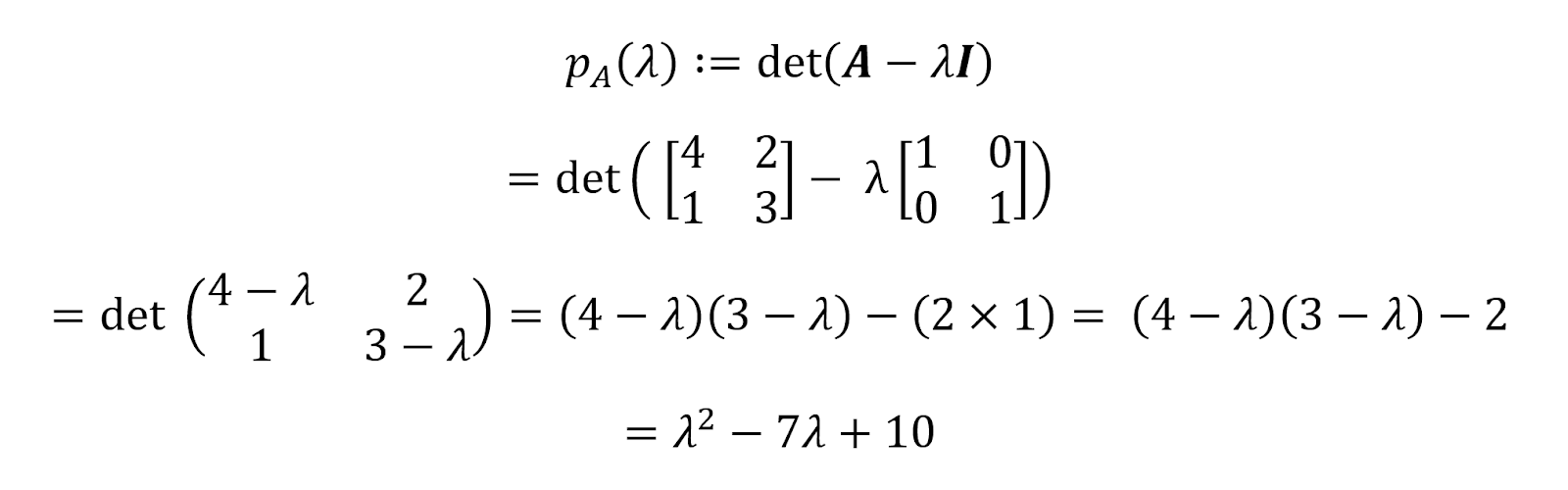
Daher istdas charakteristische Polynom für die Matrix A oben p_A(𝝀)=𝝀2-7𝝀+10. Wir können die Wurzeln dieses Polynoms finden, indem wir es mit Null gleichsetzen.

Mit der charakteristischen Gleichung Eigenwerte und Eigenvektoren finden

Ein charakteristisches Polynom einer quadratischen Matrix enthält wichtige Eigenschaften der zugehörigen Matrix, darunter die Eigenwerte und die Determinante. Daher ist es möglich, Eigenwerte aus einem charakteristischen Polynom zu extrahieren, indem man die Unbekannte löst. Oben haben wir gezeigt, wie man Eigenwerte aus dem charakteristischen Polynom für eine quadratische 2x2-Matrix A findet. Wie wir gezeigt haben, ist das charakteristische Polynom für diese Matrix:

Um den/die Eigenwert(e) zu finden, setzen wir dieses Polynom mit Null gleich und finden die Wurzeln mit algebraischen (oder rechnerischen) Methoden:

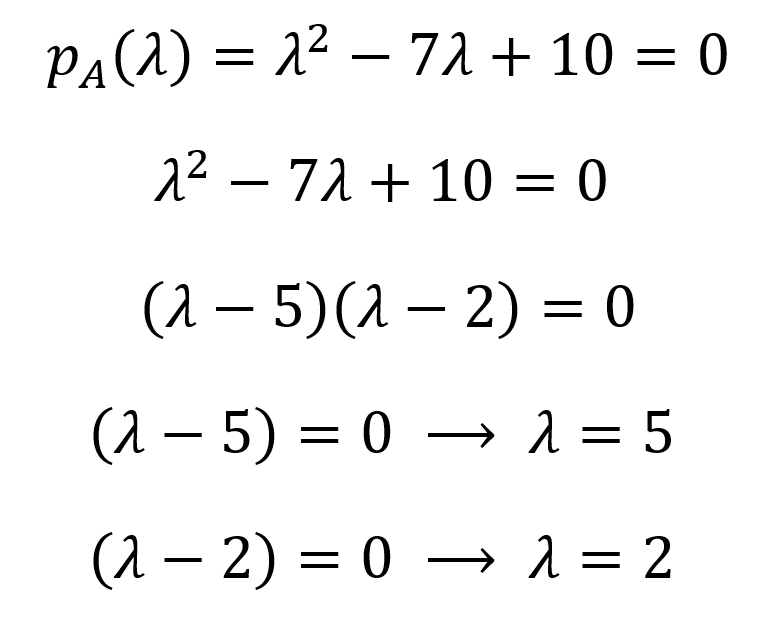
Die Eigenwerte sind also 𝝀₁=5 und 𝝀₂=2 (Eigenwerte werden üblicherweise in absteigender Reihenfolge aufgelistet, da sie die Menge an Informationen in bestimmten Datenmatrizen angeben). Die Menge aller Eigenwerte einer Matrix nennt man das Eigenspektrum oder das Spektrum dieser Matrix. Aus den Eigenwerten können wir die Eigenvektoren einer Matrix im Nullraum ableiten, indem wir (A-𝝀I)x=0 für jeden Eigenwert verwenden:

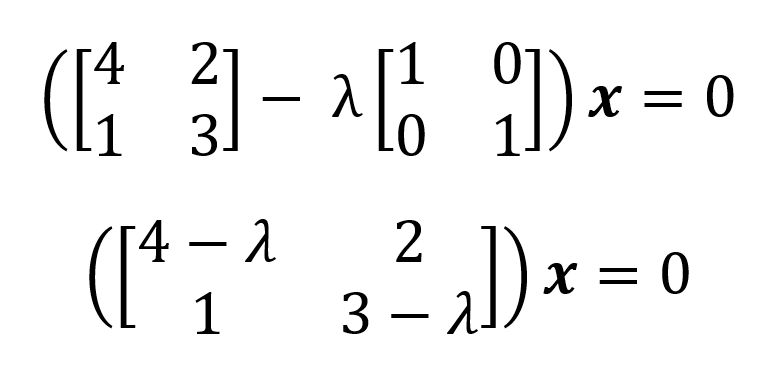
Für𝝀₁=5 setzen wir 5 ein und lösen das homogene Gleichungssystem:

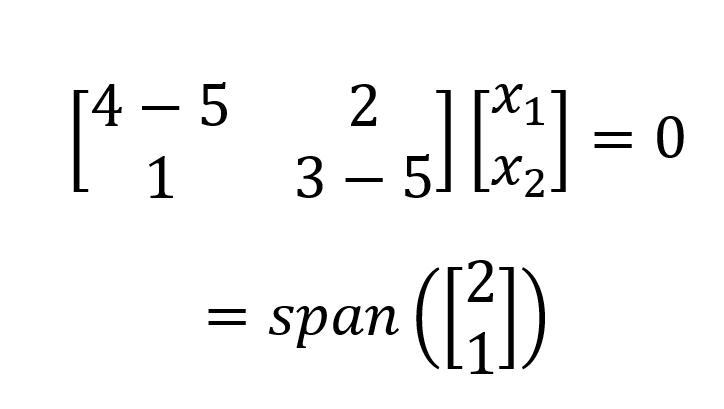
Das ergibt einen eindimensionalen (d.h. einen Basisvektor) Eigenraum. Wir führen den gleichen Prozess für 𝝀₂=2 und erhalten:

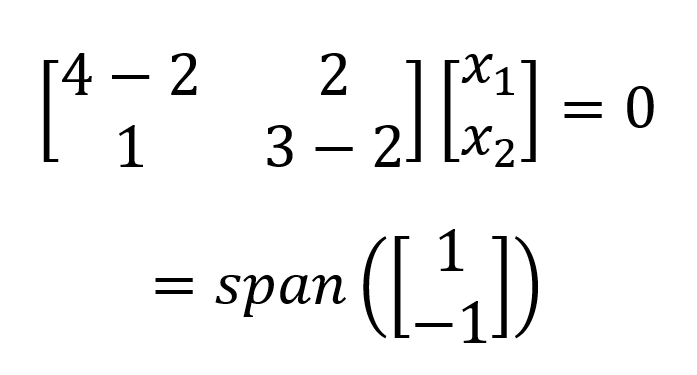
In diesem Beispiel haben wir zwei verschiedene Eigenwerte. Eine Matrix kann auch mehrere wiederholte identische Eigenwerte haben, was einen mehrdimensionalen (d.h. mehrere Basisvektoren) Eigenraum ergibt. In diesem Fall wird die Dimensionalität des Eigenraums, der von verschiedenen Eigenvektoren aufgespannt wird, als geometrische Vielfachheit des Eigenwerts i bezeichnet.

Andererseits wird die Anzahl der Wiederholungen eines Eigenwerts einer Matrix als algebraische Vielfachheit bezeichnet. Eine der interessantesten Anwendungen von Eigenwerten und Eigenvektoren ist wahrscheinlich der PageRank-Algorithmus, den Google für das Ranking von Suchergebnissen verwendet. In unserem Kurs Predictive Analytics using Networked Data in R gibt es ein interessantes Kapitel über den PageRank-Algorithmus, falls du daran interessiert bist. 

Computertechniken

Ein charakteristisches Polynom ist in der Tat ein mathematisches Polynom mit besonderen Eigenschaften (z. B. enthält es die Spur, die Determinante und die Eigenwerte einer quadratischen Matrix). Daher wird das Finden der Wurzeln der charakteristischen Gleichung mit höheren Graden von n mühsam. 

Um das charakteristische Polynom abzuleiten, musst du außerdem die Determinante der quadratischen Matrix berechnen. Obwohl wir aus pädagogischen Gründen ein Beispiel und eine Methode zur Ableitung und Lösung des charakteristischen Polynoms auf Papier und von Hand vorgestellt haben, werden in realen datenwissenschaftlichen Anwendungen numerische (rechnerische) Methoden verwendet, um die Wurzeln eines charakteristischen Polynoms zu berechnen oder zu approximieren. Laplace-Erweiterung, Gauß-Elimination und QR-Zerlegungen sind einige Methoden, mit denen die Determinanten numerisch bestimmt werden können. 

Um die Wurzeln des charakteristischen Polynoms zu finden, gibt es gängige Algorithmen wie die Newton-Raphson-Methode, die Halbierungsmethode, die Sekantenmethode und die Muller-Methode.

Anwendungen der charakteristischen Gleichung

Eigenwerte und Eigenvektoren sind grundlegende mathematische Eigenschaften von Matrizen, die sich aus einer charakteristischen Gleichung einer quadratischen Matrix ableiten lassen. In der Statistik und beim maschinellen Lernen werden charakteristische Gleichungen für verschiedene Algorithmen verwendet, die auf Eigenwerten basieren und die für die Datenreduktion und Algorithmen zur Informationsextraktion eingesetzt werden, wie z. B.:

• Hauptkomponentenanalyse (PCA) und die Dimensionalitätsreduktion, bei der ein Datensatz anhand der Werte der extrahierten Eigenwerte auf eine kleinere Anzahl von Vektoren reduziert wird.
• Spektrales ClusteringDabei handelt es sich um eine Technik, die auf dem Eigenspektrum der Ähnlichkeitsmatrix eines Datensatzes basiert, um die Dimensionalität der Daten zu reduzieren, bevor Clustering-Algorithmen wie das k-means Clustering eingesetzt werden.
• Graphentheorie und Netzwerkanalyse, bei der Eigenwerte und Eigenvektoren zur Partitionierung eines Graphen in Communities (Hauptkomponenten), zur Einbettung des Graphen in einen niedrigdimensionalen Raum zur Visualisierung und zur spektralen Sparsifizierung zur Annäherung an einen Graphen mit ähnlichem Eigenspektrum verwendet werden.
• ZeitreihenHier wird die Singulärspektralanalyse verwendet, um zugrundeliegende Muster in den Reihen zu entdecken, z. B. Trends, Zyklen und Anomalien.

Eigenschaften des charakteristischen Polynoms

Als mathematisches Objekt hat ein charakteristisches Polynom einige interessante Eigenschaften, darunter:

• Monic: Der führende Koeffizient eines charakteristischen Polynoms ist immer eins (monisch).
• Degree: Der Grad n eines charakteristischen Polynoms ist immer gleich der Größe der zugehörigen nxn-Matrix.
• Invarianz unter Matrixähnlichkeit: Wenn wir eine Matrix transformieren und das Ergebnis eine ähnliche Matrix ist, haben beide ein identisches charakteristisches Polynom (d. h. die transformierte ähnliche Matrix behält das ursprüngliche charakteristische Polynom).
• Koeffizienten: Der erste führende Term des charakteristischen Polynoms ist die Determinante der zugehörigen Matrix, und der vorletzte Koeffizient ist die vorzeichenlose Spur der zugehörigen Matrix c₀=det(A) und c_n-1=-1^n-1tr(A)
• Wenn wir im charakteristischen Polynom jede Unbekannte durch die ursprüngliche quadratische Matrix ersetzen, ist das Ergebnis eine Nullmatrix (Cayley-Hamilton-Theorem). Mit anderen Worten: Das charakteristische Polynom ist ein annihilierendes Polynom für die quadratische Matrix. In dieser Form können die Eigenwerte direkt aus der quadratischen Matrix abgeleitet werden. Daher kann man sagen, dass jede quadratische Matrix ihre eigene charakteristische Gleichung erfüllt.

Fortgeschrittene Themen

Zum Schluss möchte ich noch ein paar fortgeschrittene Details zu charakteristischen Polynomen und Matrixeigenschaften nennen, um einen weiteren Einblick in die Mathematik zu geben, ohne jedoch zu sehr ins Detail zu gehen.

• Minimales Polynom: Ein monisches Polynom, das eng mit dem charakteristischen Polynom verwandt ist, ist das minimale Polynom, ein Polynom des kleinsten positiven Grades, das die Quadratmatrix A annihiliert. Da ein charakteristisches Polynom auch seine Quadratmatrix annihilieren kann, lässt sich das Minimalpolynom von einem solchen charakteristischen Polynom ableiten.
• Ähnlichkeit und Diagonalisierung: Zwei Matrizen sind ähnlich, wenn sie durch eine gemeinsame lineare Transformation miteinander verbunden sind. Wenn zwei Matrizen ähnlich sind, dann haben sie auch den gleichen Rang, die gleiche Spur, Determinante, Eigenwerte, das charakteristische Polynom und die minimalen Polynome. 
• Charakteristische Gleichung von Matrixpotenzen und Funktionen: In einer Matrixpotenz werden die Eigenwerte zur k-ten Potenz der Matrix^Ak erhoben und das entsprechende charakteristische Polynom wird als det(A^k-λI). Für eine Matrixfunktion f(x) kann das charakteristische Polynom abgeleitet werden, indem f() an den Eigenwerten von A ausgewertet wird.

Fazit

In diesem Artikel haben wir das charakteristische Polynom kennengelernt und erfahren, wie es wichtige Eigenschaften einer quadratischen Matrix enthält, z. B. die Eigenwerte, die Spur und die Determinante. Angesichts der wichtigen Rolle, die Eigenwerte in der Datenwissenschaft und im maschinellen Lernen spielen, hilft uns das Verständnis der charakteristischen Gleichung sehr dabei, zu verstehen, wie maschinelles Lernen und statistische Algorithmen die Hauptkomponenten aus einer Datenmatrix extrahieren, um Muster zu finden und die Rechenleistung zu verbessern.

Wenn du dich für andere wichtige und bekannte Gleichungen in der Datenwissenschaft und im maschinellen Lernen interessierst, schau dir unser Tutorial zur Normalen Gleichung für lineare Regression an. DataCamp bietet auch tolle Kurse für einen umfassenden und strukturierten Lernpfad an, wie z.B. unseren Kurs Lineare Algebra für Data Science in R, den ich bereits erwähnt habe und unbedingt empfehlen kann.