Arithmetisches Mittel: Ein grundlegendes Werkzeug für die Datenanalyse

Das arithmetische Mittel, auch bekannt als "Durchschnitt", ist oft der Ausgangspunkt in der deskriptiven Statistik. Sie liefert ein schnelles, intuitives Maß für die zentrale Tendenz, das für die Interpretation von Daten in jedem Bereich wichtig ist. Das Konzept mag zwar einfach erscheinen, aber wenn du die Feinheiten des arithmetischen Mittels verstehst, kannst du echte Einblicke in komplexere Datentrends und -muster gewinnen.

Dieser Artikel bietet einen Überblick über das arithmetische Mittel und behandelt seine Formel, Anwendungen und Vergleiche mit anderen Arten von Mittelwerten. Wir werden untersuchen, warum sie häufig in der Wirtschaft, in der Datenwissenschaft und darüber hinaus verwendet wird, und auch Szenarien diskutieren, in denen alternative Maße besser geeignet sind.

Für diejenigen, die neu in der Statistik sind oder ihre Kenntnisse vertiefen wollen, bietet unser Kurs Einführung in die Statistik eine gute Grundlage. Unser Spickzettel zur deskriptiven Statistik enthält außerdem ein hilfreiches Glossar mit Begriffen zu diesem Thema.

Was ist das arithmetische Mittel?

Das arithmetische Mittel ist die Summe aller Zahlen in einem Datensatz geteilt durch die Anzahl dieser Zahlen. Diese einfache Berechnung macht ihn zu einem der intuitivsten und am häufigsten verwendeten Maße der zentralen Tendenz.

Zur Veranschaulichung wollen wir ein einfaches Beispiel betrachten. Angenommen, wir haben drei Zahlen: 5, 10, und 15. Um ihr arithmetisches Mittel zu berechnen:

1. Zähle die Zahlen zusammen: 5 + 10 + 15 = 30
2. Zähle die Zahlen: Wir haben 3 Nummern
3. Teile die Summe durch die Anzahl: 30 ÷ 3 = 10

Das arithmetische Mittel aus 5, 10 und 15 ist also 10.

Wichtige Eigenschaften des arithmetischen Mittels

Das arithmetische Mittel hat mehrere wichtige Eigenschaften, die bei näherer Betrachtung noch interessanter werden. 

Die Summe der Abweichungen ist gleich Null

Eine grundlegende Eigenschaft des arithmetischen Mittels ist, dass die Summe der Abweichungen von ihm immer gleich Null ist. Mit anderen Worten: Wenn du von jedem Datenpunkt den Mittelwert abziehst und diese Differenzen addierst, ist das Ergebnis gleich Null. Mathematisch lässt sich dies folgendermaßen ausdrücken:

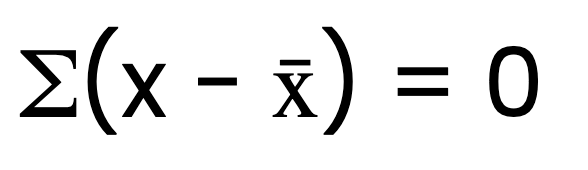
Dabei steht x für jeden Wert im Datensatz, und x̄ ist das arithmetische Mittel.

Empfindlichkeit gegenüber Ausreißern

In Datensätzen mit Extremwerten kann der arithmetische Mittelwert deutlich in Richtung dieser Ausreißer gezogen werden, was zu irreführenden Interpretationen führen kann, insbesondere bei schiefen Verteilungen. Nehmen wir zum Beispiel einen Datensatz mit Gehältern in einem kleinen Unternehmen: {$30,000, $35,000, $40,000, $45,000, $1,000,000}. Der arithmetische Mittelwert (230.000 USD) ist aufgrund des Ausreißers von 1.000.000 USD deutlich höher als die meisten Gehälter.

Diese Empfindlichkeit macht das arithmetische Mittel weniger robust als Maße wie den Median bei Ausreißern oder schiefen Verteilungen. Der Mittelwert kann aber auch nützlich sein, um das Vorhandensein von Ausreißern zu erkennen oder die Auswirkungen von Extremwerten auf einen Datensatz zu verstehen.

Auswirkungen von Änderungen der Daten

Das arithmetische Mittel reagiert vorhersehbar auf Veränderungen im Datensatz, was in verschiedenen analytischen Szenarien nützlich sein kann:

1. Addieren oder Subtrahieren einer Konstante: Wenn du von jedem Datenpunkt den gleichen Wert addierst oder subtrahierst, steigt oder sinkt der Mittelwert um genau diesen Betrag. Wenn du zum Beispiel zu jedem Wert in einem Datensatz 5 addierst, ist der neue Mittelwert 5 mehr als der ursprüngliche Mittelwert.
2. Multiplizieren oder Dividieren mit einer Konstante: Wenn du jeden Datenpunkt mit derselben Konstante, die nicht Null ist, multiplizierst oder teilst, wird der Mittelwert mit dieser Konstante multipliziert oder geteilt. Wenn du zum Beispiel jeden Wert in einem Datensatz verdoppelst, ist der neue Mittelwert doppelt so hoch wie der ursprüngliche Mittelwert.

Diese Eigenschaften machen das arithmetische Mittel besonders nützlich, wenn es um gleichmäßige Veränderungen in einem Datensatz geht, z. B. bei der Inflationsbereinigung von Wirtschaftsdaten oder der Skalierung von Messungen in wissenschaftlichen Experimenten.

Wann wird das arithmetische Mittel verwendet?

Das arithmetische Mittel ist ein vielseitiges statistisches Instrument, aber es ist in bestimmten Situationen besonders effektiv. Zunächst sollten wir sagen, dass das arithmetische Mittel besonders nützlich für Datensätze mit additiven Prozessen ist. Wenn du zum Beispiel die durchschnittliche Tagestemperatur, das Durchschnittsgehalt in einem Unternehmen oder die durchschnittlichen Testergebnisse berechnest, liefert das arithmetische Mittel eine aussagekräftige Darstellung des zentralen Wertes.

Wir sollten auch sagen, dass das arithmetische Mittel am zuverlässigsten ist, wenn die Datenpunkte gleichmäßig verteilt sind und es keine extremen Ausreißer gibt. Werfen wir einen Blick auf einige branchenspezifische Beispiele:

• Finanzen: Im Finanzwesen verlassen sich Unternehmen auf das arithmetische Mittel, um Erkenntnisse zu gewinnen und Maßstäbe zu setzen. Unternehmen nutzen es zum Beispiel, um Durchschnittsgehälter, monatliche Ausgaben und Quartalsgewinne zu ermitteln.
• Wirtschaft: Ökonomen verwenden das arithmetische Mittel, um Verbrauchertrends und Preisstabilität zu analysieren. Zu den wichtigsten Anwendungen gehören die Berechnung des Durchschnittsverbrauchs der Haushalte und die Erstellung von Indizes wie dem Verbraucherpreisindex (VPI) zur Überwachung der Inflation im Zeitverlauf.
• Gesundheitswesen und medizinische Forschung: Im Gesundheitswesen spielt das arithmetische Mittel eine wichtige Rolle bei der Bewertung von Behandlungen und der Untersuchung von Gesundheitstrends. Forscher berechnen zum Beispiel die durchschnittliche Genesungszeit und die Wirksamkeit von Medikamenten, während Epidemiologen die durchschnittliche Infektionsrate und die Überlebenszeit ermitteln.

So berechnest du das arithmetische Mittel

Nachdem wir bereits das Grundkonzept behandelt haben, wollen wir nun erkunden, wie man das arithmetische Mittel mithilfe von Tools wie R, Python und Excel berechnet werden kann, was bei größeren für größere Datensätze.

Formel für das arithmetische Mittel

Die Formel für das arithmetische Mittel lautet:

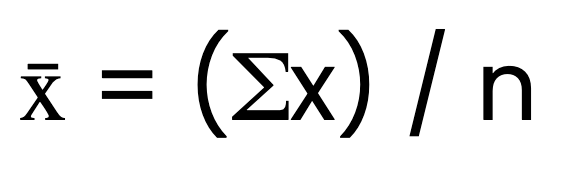
Dabei ist x̄ das arithmetische Mittel, Σx ist die Summe aller Werte und n ist die Anzahl der Werte.

Arithmetisches Mittel in Excel, Python und R

Bei größeren Datensätzen erleichtern Software-Tools die Berechnungen erheblich. Hier erfährst du, wie du das arithmetische Mittel in Excel, Python und R berechnen kannst. 

Excel

In Excel kannst du die Funktion AVERAGE() verwenden:

1. Gib deine Daten in eine Spalte oder Zeile ein.

2. Gib in eine neue Zelle =AVERAGE() ein.

3. Wähle den Bereich der Zellen aus, der deine Daten enthält.

4. Schließen Sie die Klammer und drücken Sie Eingabe.

Wenn sich deine Daten zum Beispiel in den Zellen A1:A10 befinden, würdest du verwenden: =AVERAGE(A1:A10).

Python

Das Statistikmodul von Python bietet eine Funktion mean():

from statistics import mean

data = [5, 10, 15, 20, 25]

result = mean(data)
print(result)  # Output: 15

Bei größeren Datenmengen solltest du die effizientere mean() Funktion von NumPy bevorzugen:

import numpy as np

data = np.array([5, 10, 15])

result = np.mean(data)
print(result)  # Output: 10.0

R

In R kannst du die eingebaute Funktion mean() aus Base R verwenden:

data <- c(5, 10, 15)

result <- mean(data)
print(result)  # Output: [1] 10

Diese Tools vereinfachen die Berechnung des arithmetischen Mittels für Datensätze jeder Größe, sodass du dich auf die Interpretation der Daten konzentrieren kannst, anstatt sie manuell zu berechnen.

Arithmetisches Mittel in Datenwissenschaft, maschinellem Lernen und Statistik

Die Anwendungen des arithmetischen Mittels in den Datenwissenschaften und beim maschinellen Lernen reichen von der Datenvorverarbeitung bis zur Modellbewertung. Schauen wir uns einige Schlüsselbereiche an, in denen das arithmetische Mittel besonders wichtig ist. 

Merkmal Skalierung

Eine der häufigsten Anwendungen des arithmetischen Mittels in der Datenvorverarbeitung ist die Skalierung von Merkmalen, insbesondere bei der Mittelwertzentrierung:

• Mittlere Zentrierung: Bei diesem Verfahren wird das arithmetische Mittel von jedem Datenpunkt eines Merkmals abgezogen. Das Ergebnis ist ein zentrierter Datensatz, bei dem der Mittelwert jedes Merkmals gleich Null ist. Dies kann wie folgt dargestellt werden: x_centered = x - x̄ wobei x der Originalwert und x̄ das arithmetische Mittel des Merkmals ist.

• Normung: Bei der Standardisierung, die oft in Verbindung mit der Mittelwertzentrierung verwendet wird, wird nach Abzug des Mittelwerts durch die Standardabweichung dividiert: x_standardized = (x - x̄) / σ wobei σ die Standardabweichung des Merkmals ist.

Diese Techniken helfen dabei, die Skala der Merkmale zu normalisieren, was für viele Algorithmen des maschinellen Lernens besonders wichtig ist. Wenn du mehr über den Unterschied zwischen Normalisierung und Standardisierung erfahren möchtest, kannst du dir das umfassende Tutorial ansehen.

Modellbewertung

Das arithmetische Mittel ist bei verschiedenen Modellbewertungsmetriken von grundlegender Bedeutung:

• Mittlerer quadratischer Fehler (MSE): Diese gängige Metrik für Regressionsprobleme berechnet den Durchschnitt der quadrierten Differenzen zwischen vorhergesagten und tatsächlichen Werten.
• Mittlerer absoluter Fehler (MAE): Ähnlich wie MSE, aber es wird die absolute Differenz statt der quadrierten Differenz verwendet.
• Genauigkeit: Bei Klassifizierungsproblemen wird die Genauigkeit oft als Mittelwert der richtigen Vorhersagen über alle Stichproben hinweg angegeben.

Statistik und Hypothesentests

In der statistischen Analyse wird das arithmetische Mittel oft für Hypothesentests verwendet. Zum Beispiel:

• T-Tests: Das arithmetische Mittel ist entscheidend für t-Tests, bei denen die Mittelwerte zweier Gruppen verglichen werden, um festzustellen, ob sie statistisch unterschiedlich sind. Durch den Vergleich der Stichprobenmittelwerte helfen t-Tests dabei, Hypothesen über Merkmale der Grundgesamtheit zu überprüfen.
• Konfidenzintervalle: Das arithmetische Mittel wird verwendet, um Konfidenzintervalle zu berechnen, die die Zuverlässigkeit des geschätzten Mittelwerts angeben. Dies gibt Aufschluss darüber, wie repräsentativ der Stichprobenmittelwert für die gesamte Population ist.

Andere Anwendungen

• Ensemble Methoden: Viele Ensemble-Techniken wie Bagging und Boosting verwenden das arithmetische Mittel, um Vorhersagen aus mehreren Modellen zu kombinieren.
• Gradient Descent: Das arithmetische Mittel wird bei der Berechnung des durchschnittlichen Gradienten über Mini-Batches beim stochastischen Gradientenabstieg verwendet.
• Anomalie-Erkennung: Abweichungen vom Mittelwert können genutzt werden, um Ausreißer oder Anomalien in Datensätzen zu identifizieren. Eine gängige Heuristik ist zum Beispiel die Verwendung von drei Standardabweichungen als Schwellenwert, sodass jeder Datenpunkt, der drei oder mehr Standardabweichungen vom arithmetischen Mittelwert abweicht, als Ausreißer gilt.
• Dimensionalitätsreduktion: Techniken wie die Hauptkomponentenanalyse (PCA) verwenden bei ihren Berechnungen das arithmetische Mittel, um die Daten zu zentrieren, bevor die Kovarianzmatrix berechnet wird.
• Neuronale Netze: Beim Backpropagation-Algorithmus wird das arithmetische Mittel verwendet, um den durchschnittlichen Fehler über alle Trainingsbeispiele hinweg zu berechnen.
• Kreuzvalidierung: Bei der k-fachen Kreuzvalidierung wird in der Regel das arithmetische Mittel der Leistungskennzahlen über alle Foldings als Gesamtleistung angegeben.

Wie du vielleicht schon gemerkt hast, ist das arithmetische Mittel sowohl für die Interpretation der Daten wichtig als auch ein wichtiger Vorverarbeitungsschritt, der für eine optimale Modellleistung notwendig ist. Um dein Verständnis dieser Konzepte und ihrer praktischen Anwendungen zu vertiefen, solltest du unseren Lernpfad "Machine Learning Scientist in Python " besuchen, in dem diese Themen vertieft werden.