Hauptkomponentenanalyse in R Tutorial

Einführung in die Principal Component Analysis (PCA)

Stell dir vor, dass du als Datenwissenschaftler im Einzelhandel versuchst, anhand eines Datensatzes mit den folgenden fünf Merkmalen zu verstehen , was einen Kunden glücklich macht: monatliche Ausgaben, Alter, Geschlecht, Kaufhäufigkeit und Produktbewertung. Um besser zu analysieren und umsetzbare Schlussfolgerungen zu ziehen, müssen wir den Datensatz verstehen oder ihn zumindest visualisieren. Der Mensch kann nicht mehr als drei Dimensionen visualisieren, daher ist es nicht einfach, Kundendaten mit fünf Merkmalen (Dimensionen) zu visualisieren. Hier kommt die Hauptkomponentenanalyse (kurz: PCA) ins Spiel.

"Aber was ist die Hauptkomponentenanalyse?"

Es ist ein statistischer Ansatz, mit dem man hochdimensionale Daten analysieren und die wichtigsten Informationen daraus erfassen kann. Dazu werden die ursprünglichen Daten in einen niedrigerdimensionalen Raum transformiert und hoch korrelierte Variablen zusammengeführt. In unserem Szenario würde die PCA drei Merkmale wie die monatlichen Ausgaben, die Kaufhäufigkeit und die Produktbewertung auswählen. Das könnte es einfacher machen, die Daten zu visualisieren und zu verstehen.

Nach diesem Tutorium wirst du die Hauptkomponentenanalyse besser verstehen und wissen, wie du sie mit dem berühmten corrr-Paket in R auf reale Szenarien anwenden kannst.

In diesem Video aus unserem Kurs erfährst du mehr über die Hauptkomponentenanalyse in R.

Wie funktioniert die PCA? Ein 5-Schritte-Leitfaden

Auch wenn wir uns auf die PCA konzentrieren, sollten wir uns die folgenden fünf Hauptkomponenten-Techniken vor Augen halten, die darauf abzielen, multivariate Daten zusammenzufassen und zu visualisieren. Die PCA funktioniert im Gegensatz zu den anderen Techniken nur mit quantitativen Variablen. 

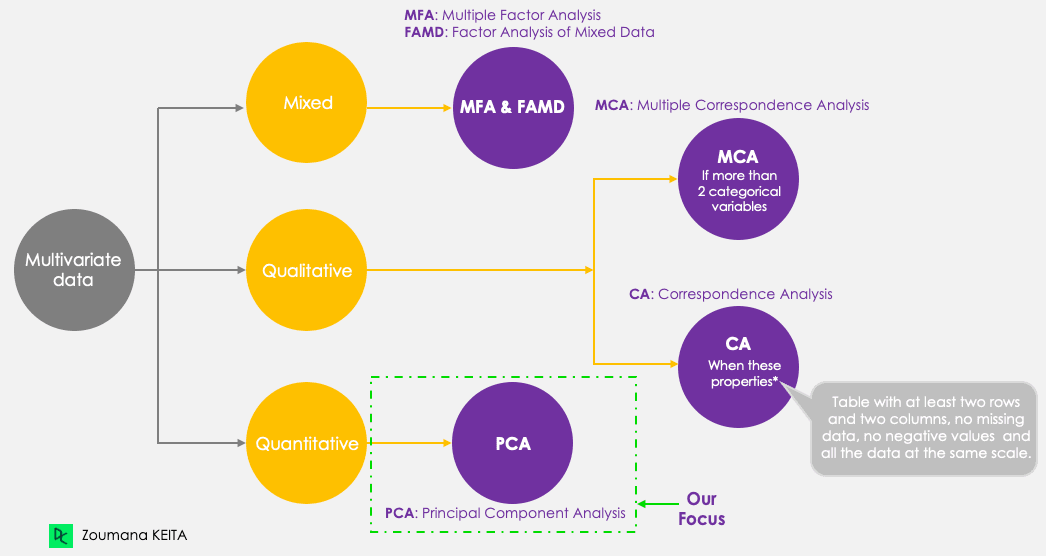
Hauptkomponenten-Methoden

Wir werden nicht auf die Erklärung des mathematischen Konzepts eingehen, das etwas komplex sein kann.  Wenn du jedoch die folgenden fünf Schritte verstehst, kannst du dir ein besseres Bild davon machen, wie man die PCA berechnet. 

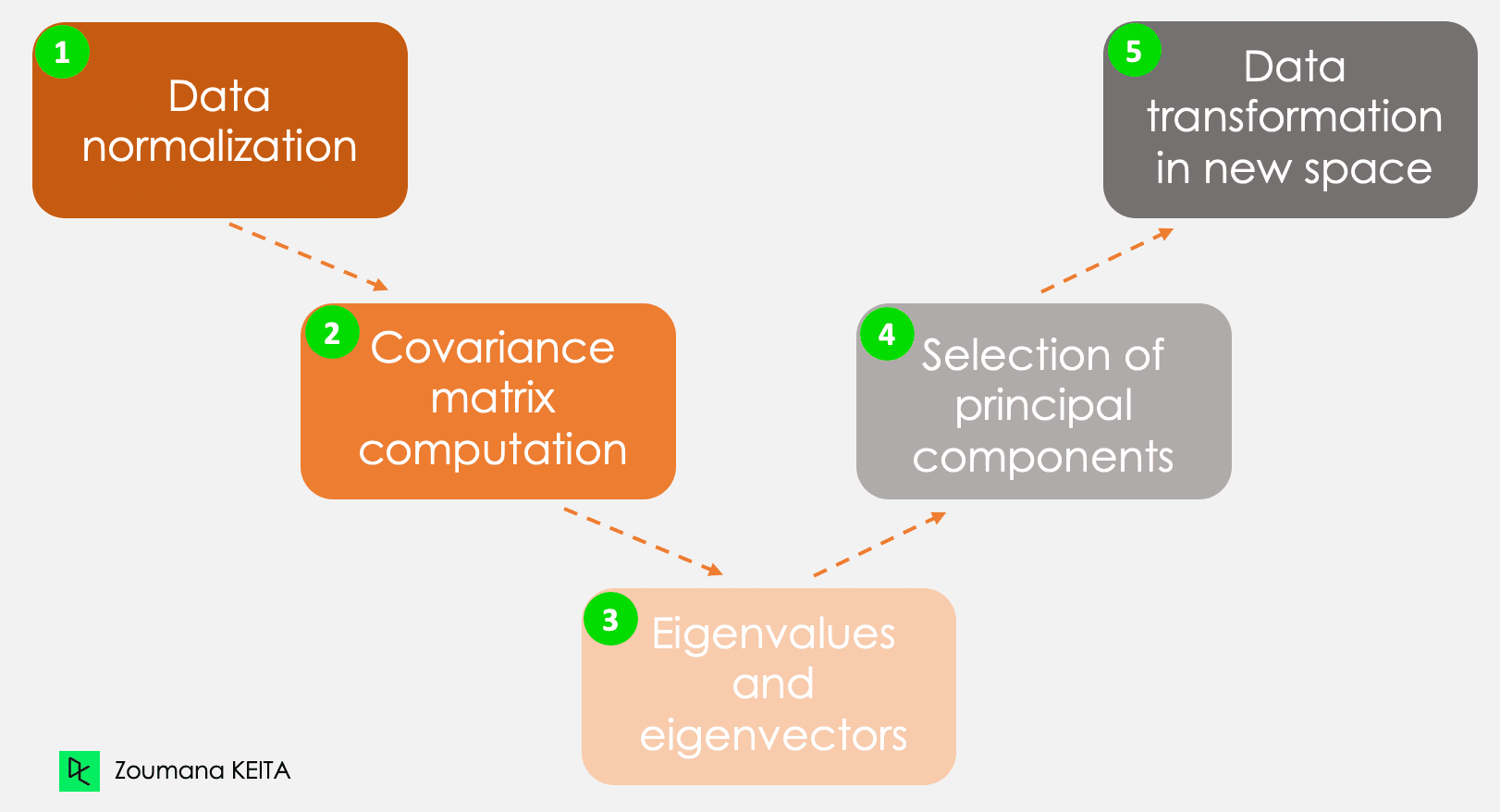
Die fünf wichtigsten Schritte zur Berechnung der Hauptkomponenten

Schritt 1 - Normalisierung der Daten

Nehmen wir das Beispiel aus der Einleitung und betrachten wir zum Beispiel die folgenden Informationen für einen bestimmten Kunden. 

• Monatliche Ausgaben: $300
• Alter: 27
• Bewertung: 4.5

Diese Informationen haben unterschiedliche Skalen und eine PCA mit solchen Daten führt zu einem verzerrten Ergebnis. Hier kommt die Normalisierung der Daten ins Spiel. So wird sichergestellt, dass jedes Attribut den gleichen Beitrag leistet und verhindert, dass eine Variable die anderen dominiert. Jede Variable wird normalisiert, indem ihr Mittelwert subtrahiert und durch ihre Standardabweichung geteilt wird.   

Schritt 2 - Kovarianzmatrix

Wie der Name schon sagt, geht es in diesem Schritt darum, die Kovarianzmatrix aus den normalisierten Daten zu berechnen. Dies ist eine symmetrische Matrix, und jedes Element (i, j) entspricht der Kovarianz zwischen den Variablen i und j.

Schritt 3 - Eigenvektoren und Eigenwerte

Geometrisch gesehen repräsentiert ein Eigenvektor eine Richtung wie "vertikal" oder "90 Grad". Ein Eigenwert hingegen ist eine Zahl, die den Anteil der Varianz in den Daten für eine bestimmte Richtung angibt. Jeder Eigenvektor hat seinen entsprechenden Eigenwert. 

Schritt 4 - Auswahl der Hauptkomponenten

Es gibt so viele Paare von Eigenvektoren und Eigenwerten wie die Anzahl der Variablen in den Daten. In den Daten, die nur die monatlichen Ausgaben, das Alter und die Rate enthalten, gibt es drei Paare. Nicht alle Paare sind relevant. Der Eigenvektor mit dem höchsten Eigenwert entspricht also der ersten Hauptkomponente. Die zweite Hauptkomponente ist der Eigenvektor mit dem zweithöchsten Eigenwert, und so weiter.

Schritt 5 - Datentransformation in den neuen dimensionalen Raum

In diesem Schritt werden die Originaldaten auf einen neuen Unterraum ausgerichtet, der durch die Hauptkomponenten definiert ist. Die Neuausrichtung erfolgt durch Multiplikation der Originaldaten mit den zuvor berechneten Eigenvektoren.

Es ist wichtig, daran zu denken, dass diese Transformation die ursprünglichen Daten selbst nicht verändert, sondern eine neue Perspektive bietet, um die Daten besser darzustellen. 

Anwendungen der Hauptkomponentenanalyse 

Die Hauptkomponentenanalyse hat eine Vielzahl von Anwendungen in unserem täglichen Leben, unter anderem (aber nicht nur) in den Bereichen Finanzen, Bildverarbeitung, Gesundheit und Sicherheit.

Finanzen

Die Vorhersage von Aktienkursen aus vergangenen Kursen ist ein Konzept, das in der Forschung seit Jahren verwendet wird. Die PCA kann zur Dimensionalitätsreduktion und zur Analyse der Daten eingesetzt werden, um Experten dabei zu helfen, relevante Komponenten zu finden, die den größten Teil der Variabilität der Daten ausmachen. Mehr über die Dimensionalitätsreduktion in R erfährst du in unserem speziellen Kurs. 

Bildbearbeitung

Ein Bild setzt sich aus mehreren Merkmalen zusammen. Die PCA wird hauptsächlich bei der Bildkomprimierung eingesetzt, um die wesentlichen Details eines Bildes zu erhalten und gleichzeitig die Anzahl der Dimensionen zu reduzieren. Darüber hinaus kann die PCA auch für kompliziertere Aufgaben wie die Bilderkennung eingesetzt werden.   

Gesundheitswesen

Nach der gleichen Logik wie bei der Bildkompression. PCA wird bei Magnetresonanztomographien (MRT) eingesetzt, um die Dimensionalität der Bilder zur besseren Visualisierung und medizinischen Analyse zu reduzieren. Sie kann auch in medizinische Technologien integriert werden, die zum Beispiel dazu dienen, eine bestimmte Krankheit anhand von Bildscans zu erkennen.

Sicherheit

Biometrische Systeme, die für die Erkennung von Fingerabdrücken verwendet werden, können Technologien integrieren, die die Hauptkomponentenanalyse nutzen, um die wichtigsten Merkmale, wie die Textur des Fingerabdrucks und zusätzliche Informationen, zu extrahieren. 

Real-World Beispiel für PCA in R

Jetzt, wo du die zugrunde liegende Theorie der PCA verstehst, bist du endlich bereit, sie in Aktion zu erleben.

Dieser Abschnitt behandelt alle Schritte von der Installation der relevanten Pakete über das Laden und Aufbereiten der Daten bis hin zur Anwendung der Hauptkomponentenanalyse in R und der Interpretation der Ergebnisse. 

Der Quellcode ist im Arbeitsbereich von DataCamp verfügbar.

Einrichten der Umgebung 

Um dieses Tutorial erfolgreich durchzuführen, brauchst du die folgenden Bibliotheken, und jede von ihnen erfordert zwei Hauptschritte, um effizient genutzt zu werden: 

• Installiere die Bibliothek, um auf alle Funktionen zugreifen zu können.
• Laden, um alle Funktionen nutzen zu können.

corrr-Paket in R

Dies ist ein R-Paket für die Korrelationsanalyse. Es konzentriert sich hauptsächlich auf die Erstellung und den Umgang mit R-Datenrahmen. Nachfolgend findest du die Schritte zum Installieren und Laden der Bibliothek. 

install.packages("corrr")
library('corrr')

ggcorrplot Paket in R

Das ggcorrplot-Paket bietet mehrere Funktionen, ist aber nicht auf die ggplot2-Funktion beschränkt, mit der sich die Korrelationsmatrix leicht visualisieren lässt. Ähnlich wie bei der obigen Anleitung ist die Installation einfach.

install.packages("ggcorrplot")
library(ggcorrplot)

FactoMineR Paket in R

Wird hauptsächlich für die multivariate explorative Datenanalyse verwendet; das factoMineR-Paket ermöglicht den Zugriff auf das PCA-Modul zur Durchführung der Hauptkomponentenanalyse. 

install.packages("FactoMineR")
library("FactoMineR")

factoextra Paket in R

Dieses letzte Paket bietet alle relevanten Funktionen, um die Ergebnisse der Hauptkomponentenanalyse zu visualisieren. Zu diesen Funktionen gehören unter anderem Scree Plot und Biplot, um nur zwei der Visualisierungstechniken zu nennen, die später im Artikel behandelt werden.

Erkundung der Daten

Bevor du die Daten lädst und weitere Untersuchungen durchführst, ist es gut, wenn du die grundlegenden Informationen zu den Daten, mit denen du arbeiten wirst, verstehst und hast.  

Protein-Daten

Der Protein-Datensatz ist ein realwertiger multivariater Datensatz, der den durchschnittlichen Proteinkonsum der Bürgerinnen und Bürger in 25 europäischen Ländern beschreibt. 

Für jedes Land gibt es zehn Spalten. Die ersten acht entsprechen den verschiedenen Arten von Proteinen. Der letzte Wert entspricht dem Gesamtwert der Durchschnittswerte der Proteine.

Verschaffen wir uns einen schnellen Überblick über die Daten. 

Zuerst laden wir die Daten mit der Funktion read.csv(), dann str(), was das folgende Bild ergibt. 

protein_data <- read.csv("protein.csv")
str(protein_data)

Wir sehen, dass der Datensatz 25 Beobachtungen und 11 Spalten hat und jede Variable numerisch ist, außer der Spalte Land, die ein Text ist. 

Beschreibung der Proteindaten

Auf Nullwerte prüfen 

Das Vorhandensein von fehlenden Werten kann das Ergebnis der PCA verfälschen. Deshalb ist es sehr empfehlenswert, diese Werte mit einem geeigneten Ansatz zu bekämpfen.  Unser Tutorial über die besten Techniken zum Umgang mit fehlenden Werten, die jeder Datenwissenschaftler kennen sollte, kann dir helfen, die richtige Wahl zu treffen. 

colSums(is.na(protein_data))

Die Funktion colSums() in Kombination mit is.na() liefert die Anzahl der fehlenden Werte in jeder Spalte. Wie wir unten sehen können, hat keine der Spalten fehlende Werte.

Anzahl der fehlenden Werte in jeder Spalte

Normalisierung der Daten

Wie zu Beginn des Artikels erwähnt, funktioniert die PCA nur mit numerischen Werten. Wir müssen also die Spalte "Land" loswerden. Auch die Spalte Gesamt ist für die Analyse nicht relevant, da sie die lineare Kombination der übrigen numerischen Variablen ist.

Der folgende Code erstellt neue Daten mit ausschließlich numerischen Spalten.

numerical_data <- protein_data[,2:10]

head(numerical_data)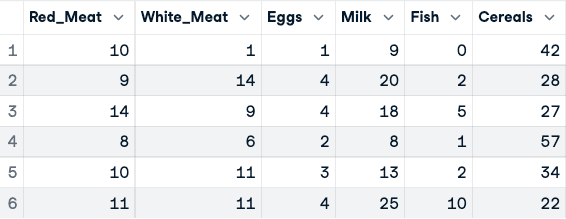

Vor der Normalisierung der Daten (nur die ersten fünf Spalten werden angezeigt)

Jetzt kann die Normalisierung mit der Funktion scale() angewendet werden. 

data_normalized <- scale(numerical_data)
head(data_normalized)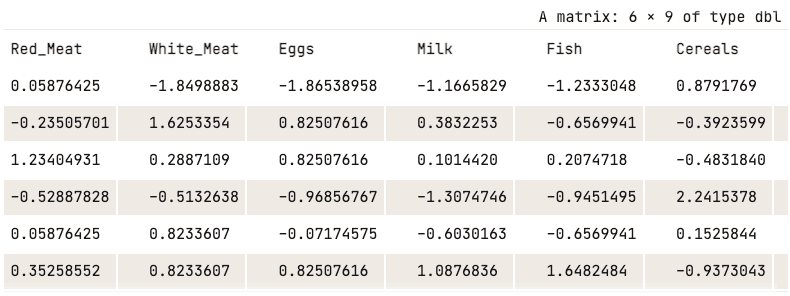

Normalisierte Daten (nur die ersten fünf Spalten werden angezeigt)

Die Anwendung der PCA

Jetzt sind alle Ressourcen verfügbar, um die PCA-Analyse durchzuführen. Zuerst berechnet princomp() die PCA, und summary() zeigt das Ergebnis an.

data.pca <- princomp(data_normalized)
summary(data.pca)

R PCA-Zusammenfassung 

Aus dem vorherigen Screenshot geht hervor, dass neun Hauptkomponenten erstellt wurden (Comp.1 bis Comp.9), die auch der Anzahl der Variablen in den Daten entsprechen.

Jede Komponente erklärt einen bestimmten Prozentsatz der Gesamtvarianz im Datensatz. Im Abschnitt über den kumulativen Anteil erklärt die erste Hauptkomponente fast 77% der Gesamtvarianz. Das bedeutet, dass fast zwei Drittel der Daten in der Gruppe der 9 Variablen durch die erste Hauptkomponente dargestellt werden können. Die zweite erklärt 12,08% der Gesamtvarianz. 

Der kumulierte Anteil von Komp.1 und Komp.2 erklärt fast 89% der Gesamtvarianz. Das bedeutet, dass die ersten beiden Hauptkomponenten die Daten genau darstellen können. 

Es ist toll, die ersten beiden Komponenten zu haben, aber was bedeuten sie wirklich? 

Diese Frage kann beantwortet werden, indem man untersucht, wie sie sich zu den einzelnen Spalten verhalten, indem man die Ladungen der einzelnen Hauptkomponenten verwendet. 

data.pca$loadings[, 1:2]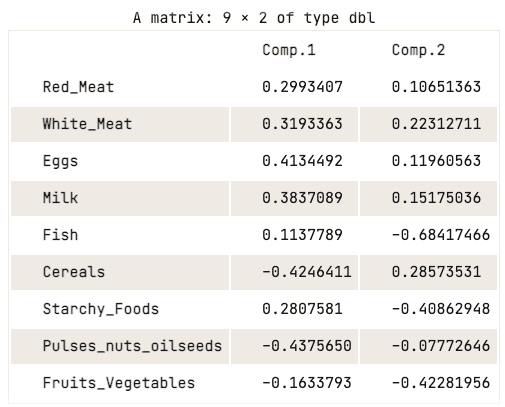

Ladematrix der ersten beiden Hauptkomponenten

Die Ladungsmatrix zeigt, dass die erste Hauptkomponente hohe positive Werte für rotes Fleisch, weißes Fleisch, Eier und Milch aufweist. Die Werte für Getreide, Hülsenfrüchte, Nüsse und Ölsaaten sowie Obst und Gemüse sind jedoch relativ negativ. Dies deutet darauf hin, dass Länder mit einer höheren Aufnahme von tierischem Eiweiß einen Überschuss aufweisen, während Länder mit einer geringeren Aufnahme ein Defizit haben.

Die zweite Hauptkomponente weist hohe negative Werte für Fisch, stärkehaltige Lebensmittel sowie Obst und Gemüse auf.  Das bedeutet, dass die Ernährung in den zugrunde liegenden Ländern stark von ihrer Lage beeinflusst wird, z. B. Küstenregionen für Fisch und Binnenregionen für eine Ernährung, die reich an Gemüse und Kartoffeln ist.

Visualisierung der Hauptkomponenten 

Die vorangegangene Analyse der Ladematrix vermittelte ein gutes Verständnis für die Beziehung zwischen jeder der ersten beiden Hauptkomponenten und den Attributen in den Daten. Aber vielleicht ist es optisch nicht so ansprechend. 

Es gibt eine Reihe von Standard-Visualisierungsstrategien, die dem Nutzer dabei helfen können, einen Einblick in die Daten zu bekommen, und in diesem Abschnitt sollen einige dieser Ansätze vorgestellt werden.  

Scree Plot

Der erste Ansatz in der Liste ist der Scree Plot. Sie wird verwendet, um die Bedeutung jeder Hauptkomponente zu visualisieren und die Anzahl der zu behaltenden Hauptkomponenten zu bestimmen. Der Scree Plot kann mit der Funktion fviz_eig() erstellt werden. 

fviz_eig(data.pca, addlabels = TRUE)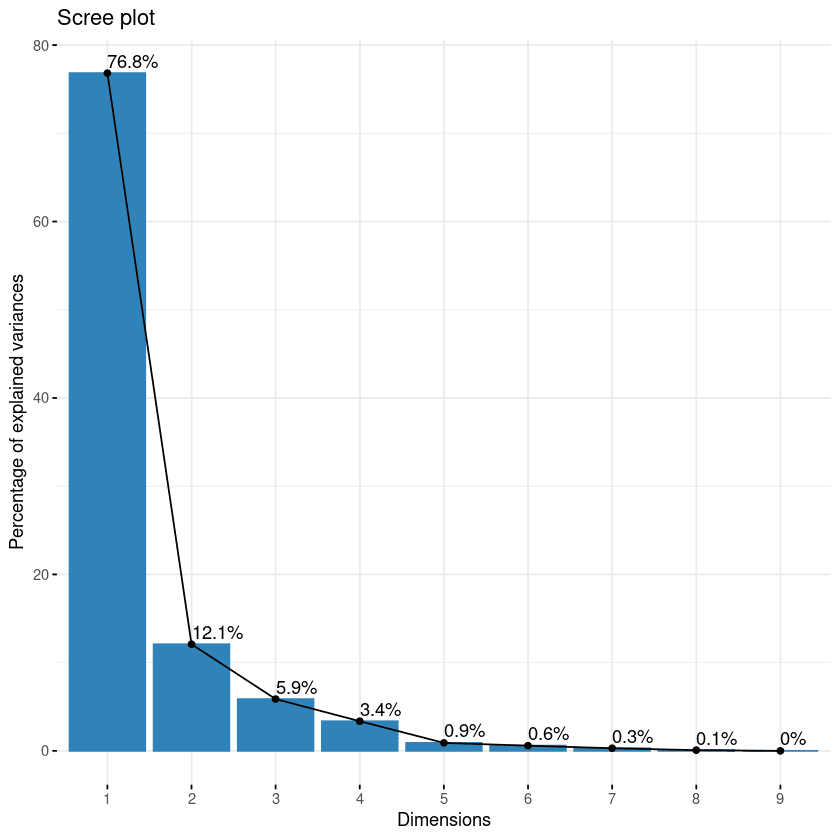

Scree Plot der Komponenten

Diese Grafik zeigt die Eigenwerte in einer Abwärtskurve, vom höchsten zum niedrigsten Wert. Die ersten beiden Komponenten können als die wichtigsten angesehen werden, da sie fast 89% der Gesamtinformationen der Daten enthalten.

Biplot der Attribute

Mit dem Biplot ist es möglich, die Ähnlichkeiten und Unähnlichkeiten zwischen den Stichproben zu visualisieren und den Einfluss jedes Attributs auf jede der Hauptkomponenten zu zeigen.

# Graph of the variables
fviz_pca_var(data.pca, col.var = "black")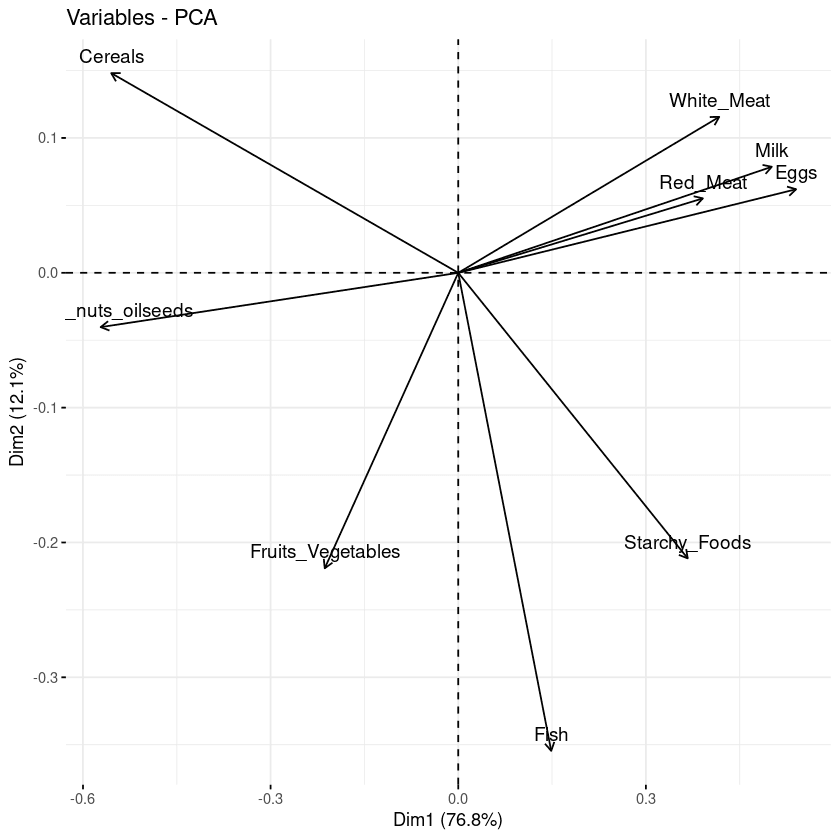

Biplot der Variablen in Bezug auf die Hauptkomponenten

Aus der vorangegangenen Grafik lassen sich drei wichtige Informationen ablesen. 

• Erstens sind alle Variablen, die in einer Gruppe zusammengefasst sind, positiv miteinander korreliert, und das ist zum Beispiel bei weißem/rotem Fleisch, Milch und Eiern der Fall. Dieses Ergebnis ist überraschend, weil sie die höchsten Werte in der Ladematrix in Bezug auf die erste Hauptkomponente haben.
• Je größer der Abstand zwischen der Variable und dem Ursprung ist, desto besser wird die Variable dargestellt. Aus dem Biplot geht hervor, dass Eier, Milch und weißes Fleisch im Vergleich zu rotem Fleisch eine höhere Größenordnung aufweisen und daher im Vergleich zu rotem Fleisch gut vertreten sind.
• Schließlich werden Variablen, die negativ korreliert sind, auf den gegenüberliegenden Seiten des Ursprungs des Biplots angezeigt. 

Beitrag der einzelnen Variablen 

Das Ziel der dritten Visualisierung ist es, festzustellen, wie stark jede Variable in einer bestimmten Komponente vertreten ist. Eine solche Darstellungsqualität wird Cos2 genannt und entspricht dem quadratischen Kosinus. Sie wird mit der Funktion fviz_cos2 berechnet.

• Ein niedriger Wert bedeutet, dass die Variable durch diese Komponente nicht perfekt repräsentiert wird. 
• Ein hoher Wert bedeutet hingegen, dass die Variable auf dieser Komponente gut dargestellt wird.

fviz_cos2(data.pca, choice = "var", axes = 1:2)

Der obige Code berechnete den quadratischen Kosinuswert für jede Variable in Bezug auf die ersten beiden Hauptkomponenten. 

Die folgende Abbildung zeigt, dass Getreide, Hülsenfrüchte, Ölsaaten, Eier und Milch die vier Variablen mit dem höchsten cos2 sind und somit den größten Beitrag zu PC1 und PC2 leisten.

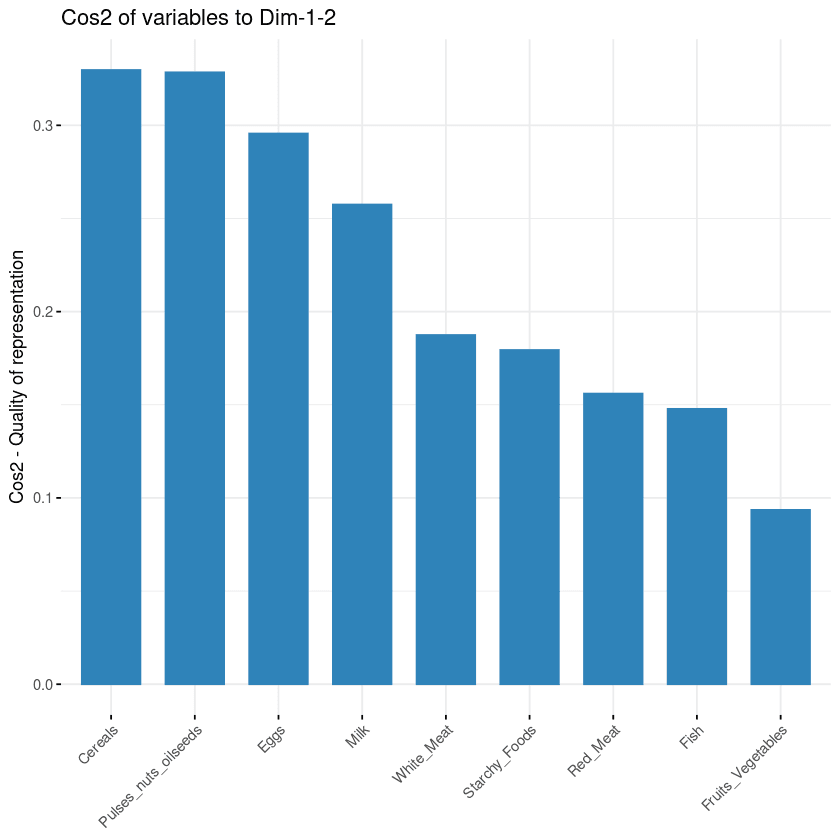
Beitrag der Variablen zu den Hauptkomponenten

Biplot kombiniert mit cos2 

Die letzten beiden Visualisierungsansätze: Biplot und Attributswichtigkeit können kombiniert werden, um ein einziges Biplot zu erstellen, in dem Attribute mit ähnlichen cos2-Werten ähnliche Farben haben.  Dies wird erreicht, indem du die Funktion fviz_pca_var wie folgt fein abstimmst:  

fviz_pca_var(data.pca, col.var = "cos2",
            gradient.cols = c("black", "orange", "green"),
            repel = TRUE)

Aus dem Biplot unten:

• Hohe cos2-Attribute sind grün gefärbt: Getreide, Hülsenfrüchte, Ölsaaten, Eier und Milch.  
• Die mittleren cos2-Attribute haben eine orange Farbe: weißes Fleisch, stärkehaltige Lebensmittel, Fisch und rotes Fleisch.
• Schließlich haben Attribute mit niedrigem cos2 eine schwarze Farbe: Obst und Gemüse, 

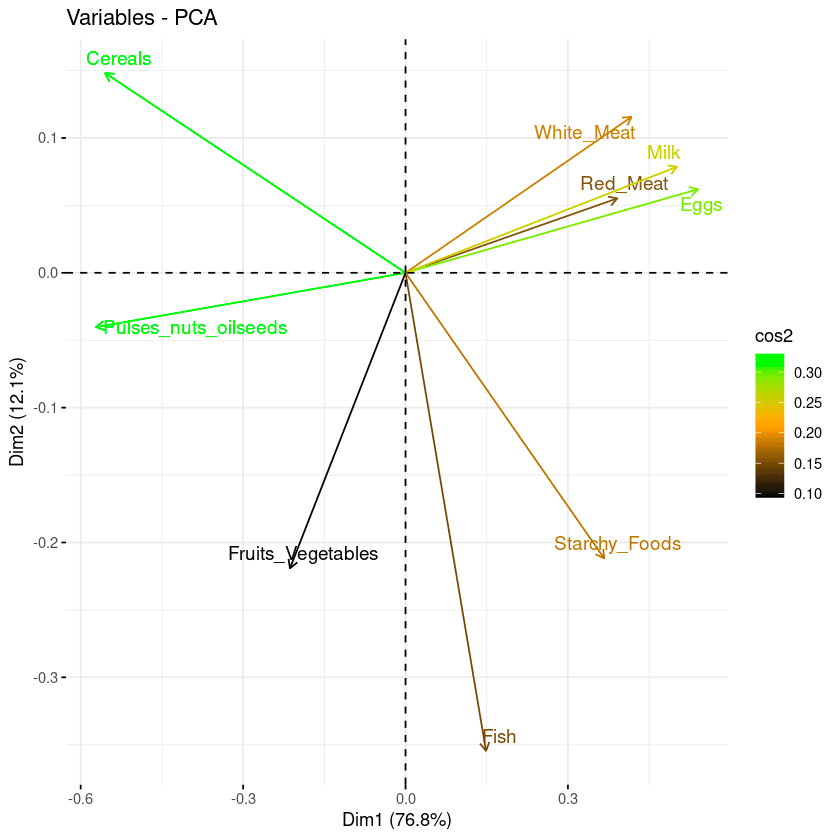
Kombination aus Biplot und cos2-Score

Fazit

In diesem Artikel haben wir uns damit beschäftigt, was die Hauptkomponentenanalyse ist und welche Bedeutung sie in der Datenanalyse hat, indem wir die Korrelationsmatrix aus dem Paket corrr verwendet haben. Zusätzlich zu den realen Anwendungen wird ein PCA-Beispiel mit verschiedenen Visualisierungsstrategien vorgestellt, von der Verwendung der bestehenden Funktion bis hin zur Feinabstimmung mit der Kombination aus biplot und cos2, um die Beziehung zwischen der PCA-Analyse in r und den Attributen besser zu verstehen und zu visualisieren. 

Wir hoffen, dass es dir die nötigen Fähigkeiten vermittelt, um die versteckten Erkenntnisse aus deinen Daten effizient zu visualisieren und zu verstehen.  

Um dein Wissen über die Hauptkomponentenanalyse zu erweitern, solltest du dir das Tutorial zur Hauptkomponentenanalyse in Python ansehen. Er veranschaulichte die Anwendung von PCA mit Python auf Tabellen- und Bilddatensätze. Unser Kurs Einführung in R ist ein guter nächster Schritt, um die Grundlagen der Datenanalyse in R zu beherrschen, einschließlich Vektoren, Listen und Datenrahmen, und R mit echten Datensätzen zu üben.