Einführung in Aktivierungsfunktionen in neuronalen Netzen

Was sind Aktivierungsfunktionen?

Aktivierungsfunktionen sind ein wesentlicher Baustein neuronaler Netze, der es ihnen ermöglicht, komplexe Muster in Daten zu lernen. Sie wandeln das Eingangssignal eines Knotens in einem neuronalen Netz in ein Ausgangssignal um, das dann an die nächste Schicht weitergegeben wird. Ohne Aktivierungsfunktionen wären neuronale Netze darauf beschränkt, nur lineare Beziehungen zwischen Eingaben und Ausgaben zu modellieren.

Aktivierungsfunktionen führen Nichtlinearitäten ein und ermöglichen es neuronalen Netzen, hochkomplexe Zuordnungen zwischen Eingaben und Ausgaben zu lernen.

Die Wahl der richtigen Aktivierungsfunktion ist entscheidend für das Training neuronaler Netze, die gut verallgemeinern und genaue Vorhersagen liefern. In diesem Beitrag geben wir einen Überblick über die gängigsten Aktivierungsfunktionen, ihre Aufgaben und die Auswahl geeigneter Aktivierungsfunktionen für verschiedene Anwendungsfälle.

Egal, ob du gerade erst mit Deep Learning anfängst oder schon ein erfahrener Praktiker bist, ein tiefes Verständnis der Aktivierungsfunktionen wird dein Gespür schärfen und deine Anwendung neuronaler Netze verbessern.

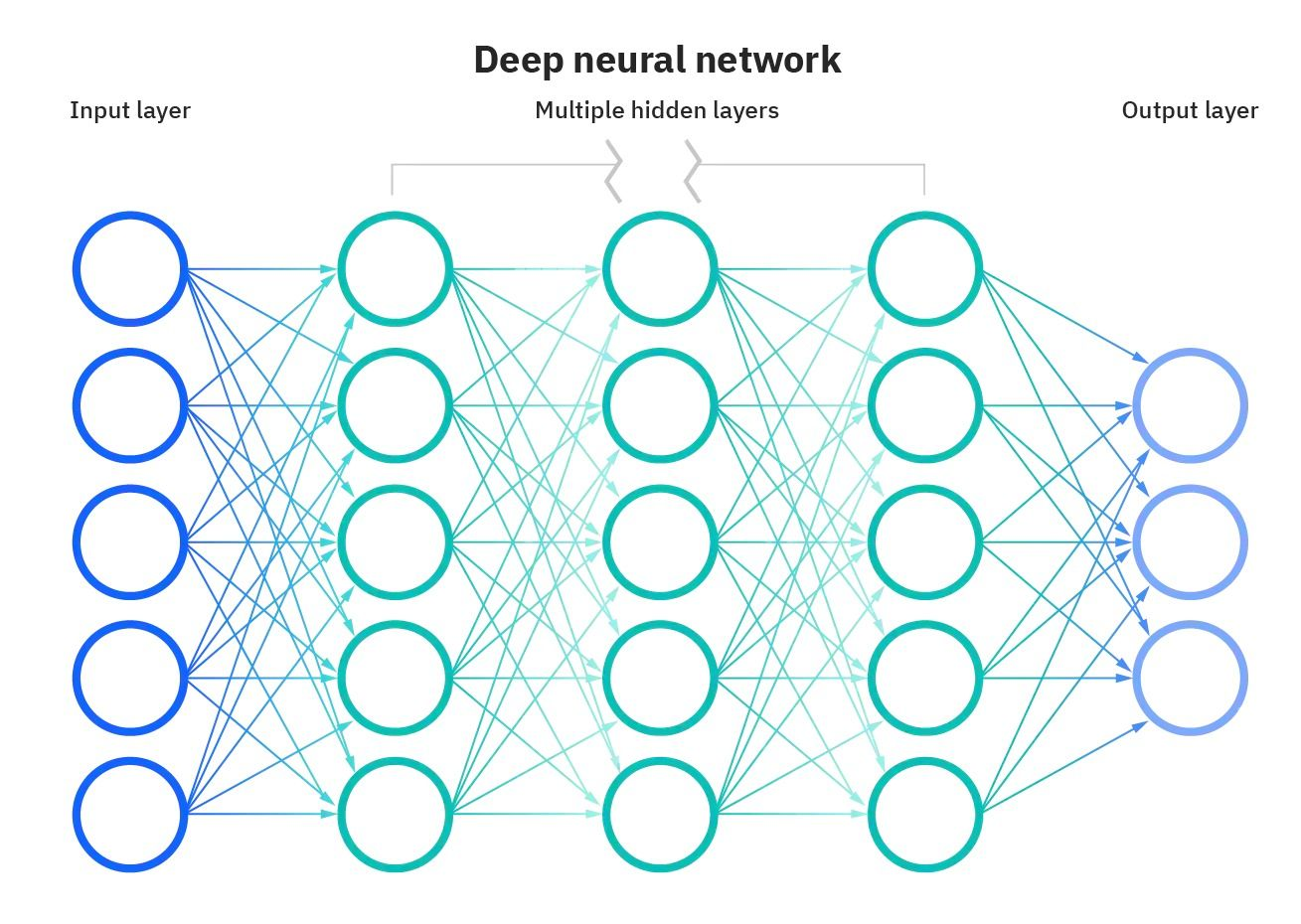
Darstellung des neuronalen Netzes Bildquelle

Warum sind Aktivierungsfunktionen wichtig?

Ohne Aktivierungsfunktionen würden neuronale Netze nur aus linearen Operationen wie Matrixmultiplikation bestehen. Alle Schichten würden lineare Transformationen des Inputs durchführen, und es würden keine Nichtlinearitäten eingeführt.

Die meisten Daten in der realen Welt sind nicht linear. So sind zum Beispiel die Beziehungen zwischen Hauspreisen und Größe, Einkommen und Käufen usw. nichtlinear. Hätten neuronale Netze keine Aktivierungsfunktionen, könnten sie die komplexen nichtlinearen Muster, die es in realen Daten gibt, nicht lernen.

Aktivierungsfunktionen ermöglichen es neuronalen Netzen, diese nichtlinearen Beziehungen zu lernen, indem sie durch Aktivierungsfunktionen nichtlineare Verhaltensweisen einführen. Dies erhöht die Flexibilität und Leistungsfähigkeit neuronaler Netze bei der Modellierung komplexer und differenzierter Daten erheblich.

Arten von Aktivierungsfunktionen

Neuronale Netze nutzen verschiedene Arten von Aktivierungsfunktionen, um Nichtlinearitäten einzuführen und das Lernen komplexer Muster zu ermöglichen. Jede Aktivierungsfunktion hat ihre eigenen einzigartigen Eigenschaften und ist für bestimmte Anwendungsfälle geeignet.

Die Sigmoid-Funktion ist zum Beispiel ideal für binäre Klassifizierungsprobleme, Softmax ist nützlich für die Vorhersage mehrerer Klassen und ReLU hilft, das Problem des verschwindenden Gradienten zu lösen.

Die Verwendung der richtigen Aktivierungsfunktion für die jeweilige Aufgabe führt zu schnellerem Training und besserer Leistung.

Schauen wir uns einige der gängigen Aktivierungsfunktionen an:

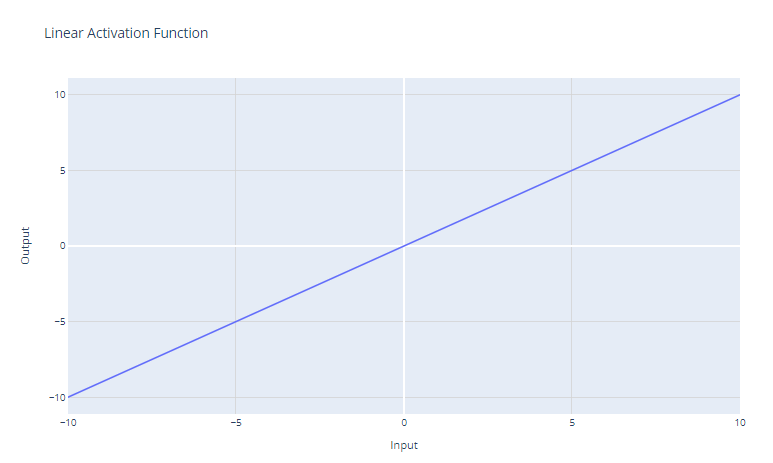
Die lineare Aktivierungsfunktion ist die einfachste Aktivierungsfunktion, definiert als:

f(x) = x

Sie gibt einfach die Eingabe x als Ausgabe zurück. Grafisch sieht das wie eine gerade Linie mit einer Steigung von 1 aus.

Der Hauptanwendungsfall der linearen Aktivierungsfunktion ist die Ausgangsschicht eines neuronalen Netzes, das für die Regression verwendet wird. Bei Regressionsproblemen, bei denen wir einen numerischen Wert vorhersagen wollen, sorgt eine lineare Aktivierungsfunktion in der Ausgabeschicht dafür, dass das neuronale Netz einen numerischen Wert ausgibt. Die lineare Aktivierungsfunktion zerquetscht oder transformiert die Ausgabe nicht, so dass der tatsächlich vorhergesagte Wert zurückgegeben wird.

Die lineare Aktivierungsfunktion wird jedoch nur selten in versteckten Schichten von neuronalen Netzen verwendet. Das liegt daran, dass es keine Nichtlinearität gibt. Der Sinn von versteckten Schichten ist es, nicht-lineare Kombinationen der Eingangsmerkmale zu lernen. Die Verwendung einer durchgängig linearen Aktivierung würde das Modell darauf beschränken, nur lineare Transformationen der Eingabe zu lernen.

Sigmoidale Aktivierung

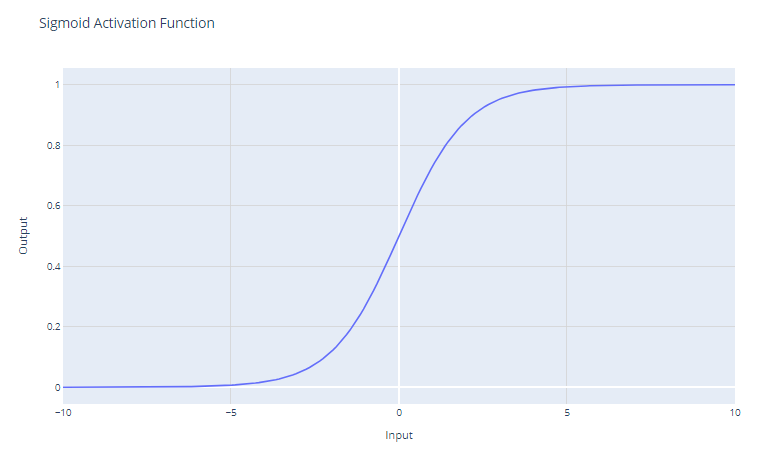
Die sigmoidale Aktivierungsfunktion, die oft als σ(x) dargestellt wird, ist eine glatte, kontinuierlich differenzierbare Funktion, die in der Entwicklung neuronaler Netze historisch wichtig ist. Die sigmoide Aktivierungsfunktion hat die mathematische Form:

f(x) = 1 / (1 + e^-x)

Sie nimmt einen reellen Wert als Eingabe und zerlegt ihn in einen Wert zwischen 0 und 1. Die Sigmoidfunktion hat eine S-förmige Kurve, die bei großen negativen Zahlen gegen 0 und bei großen positiven Zahlen gegen 1 strebt. Die Ergebnisse können leicht als Wahrscheinlichkeiten interpretiert werden, was sie für binäre Klassifizierungsprobleme geeignet macht.

Sigmoid-Einheiten waren in frühen neuronalen Netzen sehr beliebt, da der Gradient am stärksten ist, wenn die Ausgabe der Einheit nahe 0,5 liegt, was ein effizientes Backpropagation-Training ermöglicht. Allerdings leiden sigmoide Einheiten unter dem Problem des "verschwindenden Gradienten", das das Lernen in tiefen neuronalen Netzen erschwert.

Wenn die Eingabewerte deutlich positiv oder negativ werden, sättigt die Funktion bei 0 oder 1 und hat eine extrem flache Steigung. In diesen Regionen liegt die Steigung sehr nahe bei Null. Dies führt dazu, dass sich die Gewichte während der Backpropagation nur sehr geringfügig ändern, vor allem bei Neuronen in den früheren Schichten tiefer Netze, was das Lernen schmerzhaft langsam macht oder sogar zum Stillstand bringt. Dies wird als das Problem des verschwindenden Gradienten in neuronalen Netzen bezeichnet.

Der Hauptanwendungsfall der Sigmoidfunktion ist die Aktivierung der Ausgabeschicht von binären Klassifikationsmodellen. Er zerlegt die Ausgabe in einen Wahrscheinlichkeitswert zwischen 0 und 1, der als die Wahrscheinlichkeit der Zugehörigkeit der Eingabe zu einer bestimmten Klasse interpretiert werden kann.

Tanh (Hyperbolischer Tangens) Aktivierung

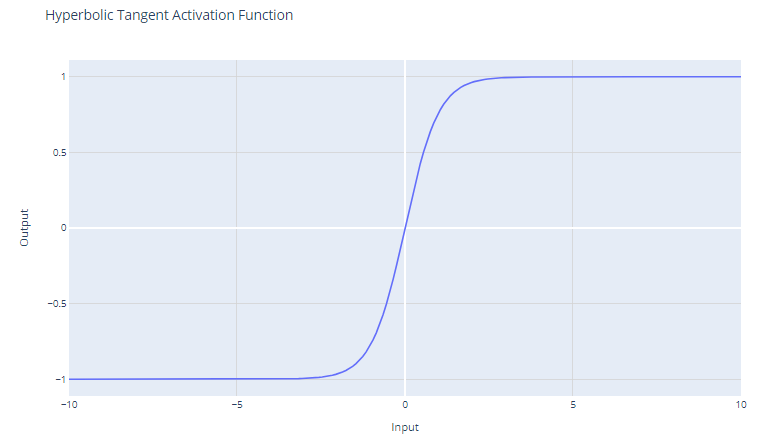
Die Aktivierungsfunktion tanh (hyperbolischer Tangens) ist definiert als:

f(x) = (e^x - e^-x) / (e^x + e^-x)

Die tanh-Funktion gibt Werte im Bereich von -1 bis +1 aus. Das bedeutet, dass sie mit negativen Werten besser umgehen kann als die Sigmoidfunktion, die einen Bereich von 0 bis 1 hat.

Im Gegensatz zur Sigmoid-Funktion ist tanh null-zentriert, was bedeutet, dass ihre Ausgabe symmetrisch um den Ursprung des Koordinatensystems ist. Dies wird oft als Vorteil angesehen, weil der Lernalgorithmus dadurch schneller konvergieren kann.

Da die Ausgabe von tanh zwischen -1 und +1 liegt, hat sie stärkere Steigungen als die Sigmoidfunktion. Stärkere Gradienten führen oft zu einem schnelleren Lernen und einer schnelleren Konvergenz während des Trainings, da sie im Vergleich zu den Gradienten der Sigmoidfunktion widerstandsfähiger gegen das Problem der verschwindenden Gradienten sind.

Trotz dieser Vorteile leidet die tanh-Funktion immer noch unter dem Problem des verschwindenden Gradienten. Während der Backpropagation können die Gradienten der tanh-Funktion sehr klein werden (nahe bei Null). Dieses Problem ist besonders problematisch bei tiefen Netzen mit vielen Schichten; die Gradienten der Verlustfunktion können zu klein werden, um während des Trainings signifikante Änderungen an den Gewichten vorzunehmen, wenn sie zu den ersten Schichten zurückwandern. Dies kann den Trainingsprozess drastisch verlangsamen und zu schlechten Konvergenzeigenschaften führen.

Die tanh-Funktion wird häufig in den versteckten Schichten eines neuronalen Netzes verwendet. Wenn die Daten außerdem auf einen Mittelwert von Null normalisiert werden, kann dies zu einem effizienteren Training führen, da die Daten nullzentriert sind.

Wenn man sich zwischen dem Sigmoid und dem tanh entscheiden muss und keinen besonderen Grund hat, das eine dem anderen vorzuziehen, ist das tanh aus den oben genannten Gründen oft die bessere Wahl. Die Entscheidung kann jedoch auch durch den spezifischen Anwendungsfall und das Verhalten des Netzes während der ersten Trainingsexperimente beeinflusst werden.

Du kannst ein einfaches neuronales Netzwerk von Grund auf mit PyTorch aufbauen, indem du unserem Tutorial von Kurtis Pykes folgst. Wenn du ein fortgeschrittener Nutzer bist, ist unser Kurs Deep Learning mit PyTorch genau das Richtige für dich. .

ReLU (Rectified Linear Unit)-Aktivierung

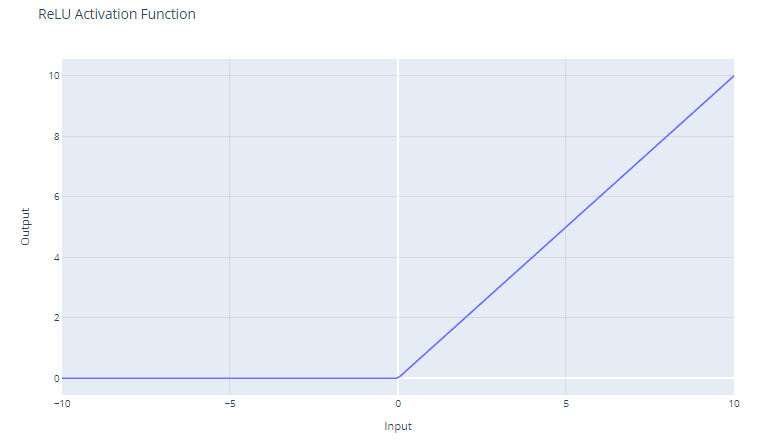
Die Aktivierungsfunktion der Rectified Linear Unit (ReLU) hat die Form:

f(x) = max(0, x)

Sie setzt den Schwellenwert für die Eingabe auf Null und gibt bei negativen Werten 0 und bei positiven Werten die Eingabe selbst zurück.

Für Eingaben, die größer als 0 sind, wirkt ReLU wie eine lineare Funktion mit einer Steigung von 1. Das bedeutet, dass sie die Skala der positiven Eingaben nicht verändert und den Gradienten während der Backpropagation unverändert durchlässt. Diese Eigenschaft ist wichtig, um das Problem des verschwindenden Gradienten zu entschärfen.

Auch wenn ReLU für die Hälfte des Eingaberaums linear ist, handelt es sich technisch gesehen um eine nichtlineare Funktion, weil sie bei x=0 einen nicht differenzierbaren Punkt hat, an dem sie abrupt von x abweicht. Diese Nichtlinearität ermöglicht es neuronalen Netzen, komplexe Muster zu lernen

Da ReLU für alle negativen Eingaben den Wert Null ausgibt, führt es natürlich zu spärlichen Aktivierungen; zu jeder Zeit wird nur eine Teilmenge der Neuronen aktiviert, was zu effizienteren Berechnungen führt.

Die ReLU-Funktion ist rechnerisch kostengünstig, weil sie einen einfachen Schwellenwert von Null hat. Dadurch können Netzwerke auf viele Schichten skaliert werden, ohne dass der Rechenaufwand im Vergleich zu komplexeren Funktionen wie tanh oder sigmoid erheblich steigt.

Softmax-Aktivierung

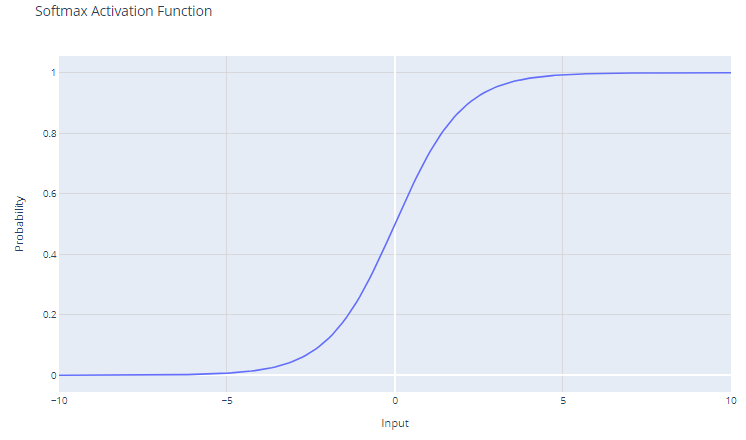
Die Softmax-Aktivierungsfunktion, die auch als normalisierte Exponentialfunktion bekannt ist, ist besonders nützlich im Zusammenhang mit Mehrklassen-Klassifizierungsproblemen. Diese Funktion arbeitet mit einem Vektor, der oft als Logits bezeichnet wird und die Rohvorhersagen oder Punktzahlen für jede Klasse darstellt, die von den vorherigen Schichten eines neuronalen Netzes berechnet wurden.

Für einen Eingangsvektor x mit den Elementen x1, x2, ..., xC ist die Softmax-Funktion definiert als:

f(xi) = e^xi / Σj e^xj

Das Ergebnis der Softmax-Funktion ist eine Wahrscheinlichkeitsverteilung, die sich zu eins summiert. Jedes Element der Ausgabe steht für die Wahrscheinlichkeit, dass die Eingabe zu einer bestimmten Klasse gehört.

Durch die Verwendung der Exponentialfunktion wird sichergestellt, dass alle Ausgabewerte nicht-negativ sind. Das ist wichtig, weil Wahrscheinlichkeiten nicht negativ sein können.

Softmax verstärkt die Unterschiede im Eingangsvektor. Selbst kleine Unterschiede bei den Eingabewerten können zu erheblichen Unterschieden bei den Ausgabewahrscheinlichkeiten führen, wobei der/die höchste(n) Eingabewert(e) in der resultierenden Wahrscheinlichkeitsverteilung tendenziell dominieren.

Softmax wird in der Regel in der Ausgabeschicht eines neuronalen Netzes verwendet, wenn die Aufgabe darin besteht, eine Eingabe in eine von mehreren (mehr als zwei) möglichen Kategorien zu klassifizieren (Mehrklassen-Klassifizierung).

Die von der Softmax-Funktion erzeugten Wahrscheinlichkeiten können als Konfidenzwerte für jede Klasse interpretiert werden und geben Aufschluss darüber, wie sicher das Modell bei seinen Vorhersagen ist.

Da Softmax die Unterschiede verstärkt, kann es empfindlich auf Ausreißer oder Extremwerte reagieren. Wenn der Eingabevektor zum Beispiel einen sehr großen Wert hat, kann Softmax die Wahrscheinlichkeiten anderer Klassen "zerquetschen", was zu einem übermäßig zuverlässigen Modell führt.

Die Wahl der richtigen Aktivierungsfunktion

Die Wahl der Aktivierungsfunktion hängt von der Art des Problems ab, das du zu lösen versuchst. Hier sind einige Richtlinien:

Für die binäre Klassifizierung:

Verwende die Sigmoid-Aktivierungsfunktion in der Ausgabeschicht. Es wird Ausgaben zwischen 0 und 1 ausgeben, die Wahrscheinlichkeiten für die beiden Klassen darstellen.

Für die Mehrklassen-Klassifizierung:

Verwende die Softmax-Aktivierungsfunktion in der Ausgabeschicht. Es gibt Wahrscheinlichkeitsverteilungen über alle Klassen aus.

Wenn du unsicher bist:

Verwende die ReLU-Aktivierungsfunktion in den versteckten Schichten. ReLU ist die gängigste Standard-Aktivierungsfunktion und normalerweise eine gute Wahl.

Fazit

Wir haben erforscht, welche zentrale Rolle Aktivierungsfunktionen beim Training neuronaler Netze spielen. Wir haben gesehen, dass sie nicht nur optionale Extras sind, sondern wesentliche Elemente, die es neuronalen Netzen ermöglichen, die Komplexität realer Daten zu erfassen und zu modellieren. Von der einfachen, aber effektiven ReLU bis zu den probabilistischen Interpretationen der Softmax-Funktion hat jede Aktivierungsfunktion ihren Platz und ihren Zweck in den verschiedenen Schichten eines Netzes und in verschiedenen Problembereichen.

Mit der weiteren Entwicklung neuronaler Netze wird sich die Erforschung von Aktivierungsfunktionen zweifellos ausweiten und möglicherweise auch neue Formen umfassen, die spezifische Herausforderungen neuer Architekturen angehen. Die in diesem Blog besprochenen Prinzipien und Funktionen werden jedoch wahrscheinlich auf absehbare Zeit der Kern des Designs neuronaler Netze bleiben.

Die sorgfältige Auswahl von Aktivierungsfunktionen ist ein Balanceakt - eine Mischung aus wissenschaftlichem Verständnis und künstlerischer Intuition - der die Leistung neuronaler Netze erheblich beeinflussen kann.

Bist du daran interessiert, Deep Learning mit dem Keras-Framework zu lernen? Schau dir unseren Kurs Einführung in Deep Learning mit Keras an.