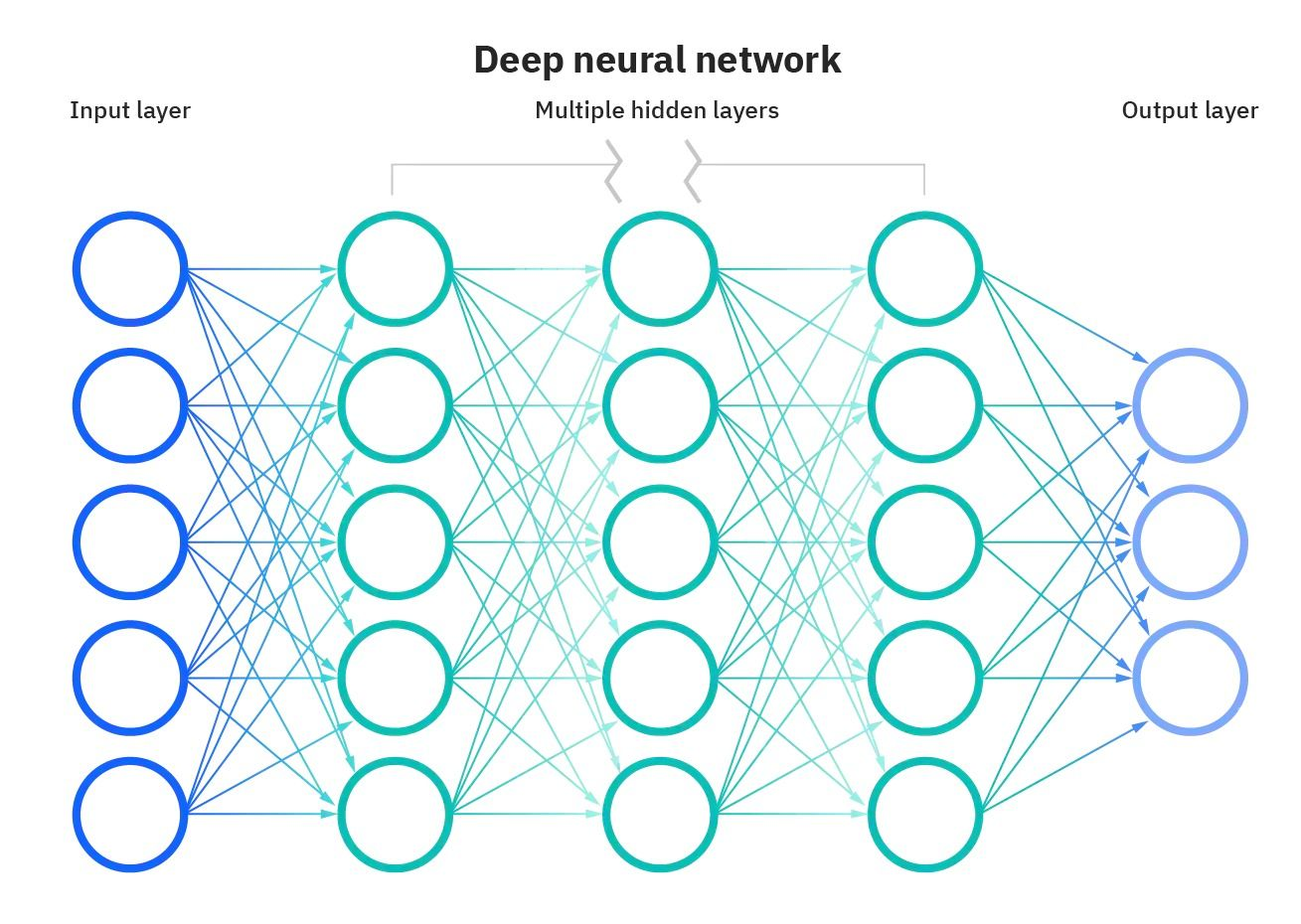
Représentation d'un réseau neuronal Source de l'image
Que sont les fonctions d'activation ?
Les fonctions d'activation font partie intégrante des réseaux neuronaux et leur permettent d'apprendre des schémas complexes dans les données. Ils transforment le signal d'entrée d'un nœud d'un réseau neuronal en un signal de sortie qui est ensuite transmis à la couche suivante. Sans fonctions d'activation, les réseaux neuronaux seraient limités à la modélisation de relations linéaires entre les entrées et les sorties.
Les fonctions d'activation introduisent des non-linéarités, ce qui permet aux réseaux neuronaux d'apprendre des correspondances très complexes entre les entrées et les sorties.
Le choix de la bonne fonction d'activation est crucial pour former des réseaux neuronaux qui généralisent bien et fournissent des prédictions précises. Dans ce billet, nous vous proposons une vue d'ensemble des fonctions d'activation les plus courantes, de leur rôle et de la manière de sélectionner des fonctions d'activation adaptées à différents cas d'utilisation.
Que vous débutiez dans l'apprentissage profond ou que vous soyez un praticien chevronné, une compréhension approfondie des fonctions d'activation renforcera votre intuition et améliorera votre application des réseaux neuronaux.
Pourquoi les fonctions d'activation sont-elles essentielles ?
Sans fonctions d'activation, les réseaux neuronaux se limiteraient à des opérations linéaires telles que la multiplication de matrices. Toutes les couches effectueraient des transformations linéaires de l'entrée et aucune non-linéarité ne serait introduite.
La plupart des données du monde réel ne sont pas linéaires. Par exemple, les relations entre les prix des logements et la taille, le revenu, les achats, etc. ne sont pas linéaires. Si les réseaux neuronaux n'avaient pas de fonctions d'activation, ils ne parviendraient pas à apprendre les modèles non linéaires complexes qui existent dans les données du monde réel.
Les fonctions d'activation permettent aux réseaux neuronaux d'apprendre ces relations non linéaires en introduisant des comportements non linéaires par le biais de fonctions d'activation. Cela augmente considérablement la flexibilité et la puissance des réseaux neuronaux pour modéliser des données complexes et nuancées.
Types de fonctions d'activation
Les réseaux neuronaux utilisent différents types de fonctions d'activation pour introduire des non-linéarités et permettre l'apprentissage de modèles complexes. Chaque fonction d'activation possède ses propres propriétés et convient à certains cas d'utilisation.
Par exemple, la fonction sigmoïde est idéale pour les problèmes de classification binaire, la fonction softmax est utile pour les prédictions multi-classes et la fonction ReLU permet de surmonter le problème du gradient qui s'évanouit.
L'utilisation de la fonction d'activation adaptée à la tâche permet d'accélérer l'apprentissage et d'améliorer les performances.
Examinons quelques-unes des fonctions d'activation les plus courantes :
Activation linéaire
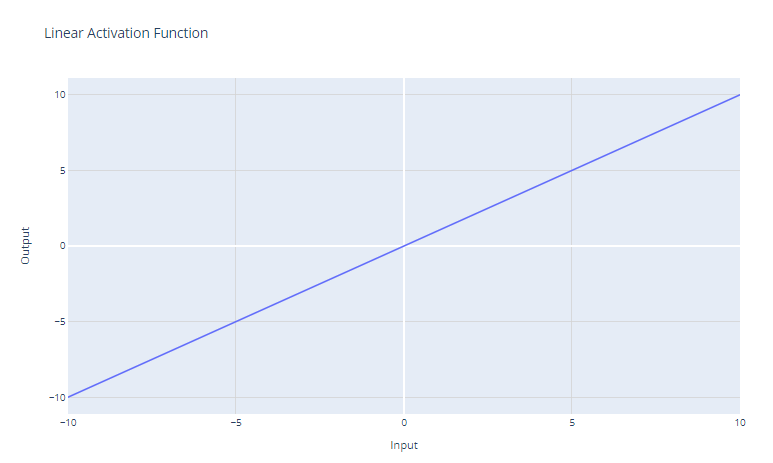
Fonction d'activation linéaire. Image par l'auteur
La fonction d'activation linéaire est la fonction d'activation la plus simple, définie comme suit :
f(x) = x
Il renvoie simplement l'entrée x en tant que sortie. Graphiquement, elle ressemble à une ligne droite avec une pente de 1.
Le principal cas d'utilisation de la fonction d'activation linéaire est la couche de sortie d'un réseau neuronal utilisé pour la régression. Pour les problèmes de régression où l'on souhaite prédire une valeur numérique, l'utilisation d'une fonction d'activation linéaire dans la couche de sortie permet au réseau neuronal de produire une valeur numérique. La fonction d'activation linéaire n'écrase ni ne transforme la sortie, de sorte que la valeur prédite réelle est renvoyée.
Cependant, la fonction d'activation linéaire est rarement utilisée dans les couches cachées des réseaux neuronaux. Cela s'explique par le fait qu'il n'y a pas de non-linéarité. L'intérêt des couches cachées est d'apprendre des combinaisons non linéaires des caractéristiques d'entrée. L'utilisation d'une activation linéaire à tous les niveaux limiterait le modèle à l'apprentissage de transformations linéaires de l'entrée.
Activation du sigmoïde
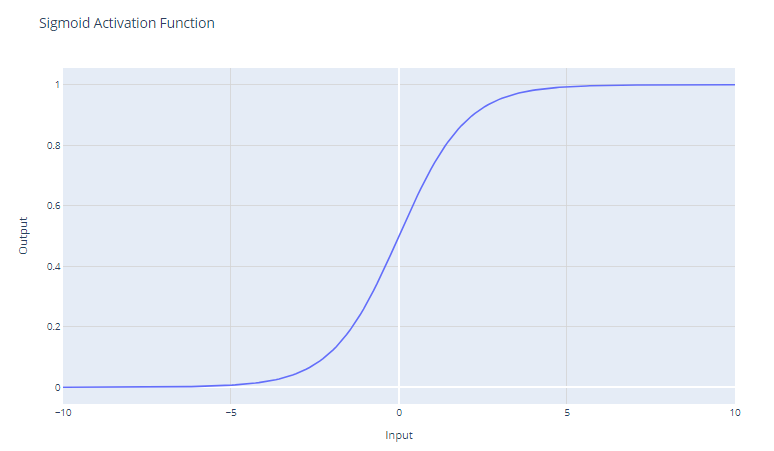
Fonction d'activation sigmoïde. Image par l'auteur
La fonction d'activation sigmoïde, souvent représentée par σ(x), est une fonction lisse et continuellement différentiable, historiquement importante dans le développement des réseaux neuronaux. La fonction d'activation sigmoïde a la forme mathématique suivante :
f(x) = 1 / (1 + e^-x)
Il prend une valeur réelle en entrée et la réduit à une valeur comprise entre 0 et 1. La fonction sigmoïde a une courbe en forme de "S" qui asymptote à 0 pour les grands nombres négatifs et à 1 pour les grands nombres positifs. Les résultats peuvent être facilement interprétés comme des probabilités, ce qui le rend naturel pour les problèmes de classification binaire.
Les unités sigmoïdes étaient populaires dans les premiers réseaux neuronaux car le gradient est le plus fort lorsque la sortie de l'unité est proche de 0,5, ce qui permet un apprentissage efficace par rétropropagation. Cependant, les unités sigmoïdes souffrent du problème du "gradient disparaissant" qui entrave l'apprentissage dans les réseaux neuronaux profonds.
Lorsque les valeurs d'entrée deviennent significativement positives ou négatives, la fonction sature à 0 ou 1, avec une pente extrêmement plate. Dans ces régions, le gradient est très proche de zéro. Cela se traduit par de très faibles changements dans les poids pendant la rétropropagation, en particulier pour les neurones des premières couches des réseaux profonds, ce qui ralentit douloureusement l'apprentissage, voire l'interrompt. C'est ce que l'on appelle le problème de la disparition du gradient dans les réseaux neuronaux.
La fonction sigmoïde est principalement utilisée comme activation de la couche de sortie des modèles de classification binaire. Il réduit la sortie à une valeur de probabilité comprise entre 0 et 1, qui peut être interprétée comme la probabilité que l'entrée appartienne à une classe particulière.
Activation du Tanh (tangente hyperbolique)
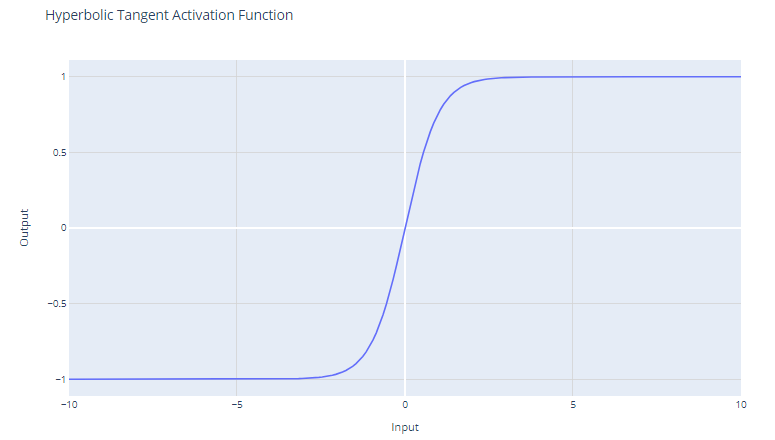
Fonction d'activation Tanh. Image par l'auteur
La fonction d'activation tanh (tangente hyperbolique) est définie comme suit :
f(x) = (e^x - e^-x) / (e^x + e^-x)
La fonction tanh produit des valeurs comprises entre -1 et +1. Cela signifie qu'elle peut traiter les valeurs négatives plus efficacement que la fonction sigmoïde, dont la plage est comprise entre 0 et 1.
Contrairement à la fonction sigmoïde, tanh est centrée sur le zéro, ce qui signifie que sa sortie est symétrique par rapport à l'origine du système de coordonnées. Ceci est souvent considéré comme un avantage car cela peut aider l'algorithme d'apprentissage à converger plus rapidement.
Comme la sortie de tanh se situe entre -1 et +1, ses gradients sont plus forts que ceux de la fonction sigmoïde. Des gradients plus forts permettent souvent un apprentissage et une convergence plus rapides pendant l'apprentissage, car ils ont tendance à mieux résister au problème des gradients qui s'évanouissent, par rapport aux gradients de la fonction sigmoïde.
Malgré ces avantages, la fonction tanh souffre toujours du problème de la disparition du gradient. Au cours de la rétropropagation, les gradients de la fonction tanh peuvent devenir très faibles (proches de zéro). Cette question est particulièrement problématique pour les réseaux profonds comportant de nombreuses couches ; les gradients de la fonction de perte peuvent devenir trop faibles pour apporter des changements significatifs aux poids pendant la formation, car ils se propagent vers les couches initiales. Cela peut ralentir considérablement le processus d'apprentissage et entraîner de mauvaises propriétés de convergence.
La fonction tanh est fréquemment utilisée dans les couches cachées d'un réseau neuronal. En raison de sa nature centrée sur le zéro, lorsque les données sont également normalisées pour avoir une moyenne nulle, la formation peut être plus efficace.
Si l'on doit choisir entre la sigmoïde et la tanh sans raison particulière de préférer l'une à l'autre, la tanh est souvent le meilleur choix pour les raisons mentionnées ci-dessus. Toutefois, la décision peut également être influencée par le cas d'utilisation spécifique et le comportement du réseau lors des premières expériences de formation.
Vous pouvez construire un réseau neuronal simple à partir de zéro à l'aide de PyTorch en suivant notre tutoriel de Kurtis Pykes, ou, si vous êtes un utilisateur avancé, notre cours de Cours sur l'apprentissage profond avec PyTorch est fait pour vous. .
Activation de l'unité linéaire rectifiée (ReLU)
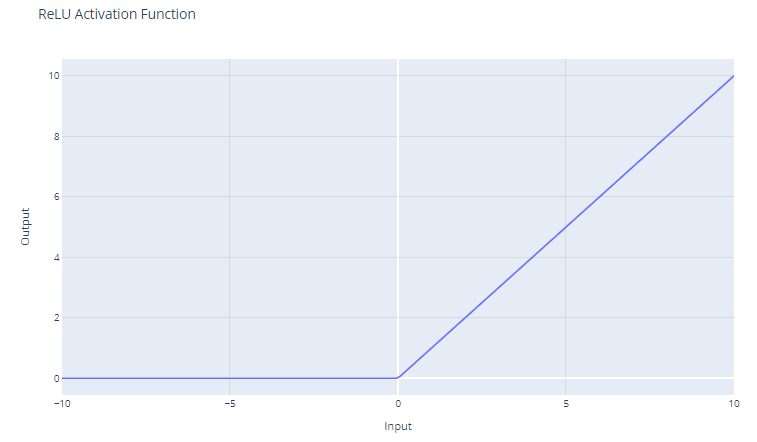
Fonction d'activation ReLU (Rectified Linear Unit). Image par l'auteur
La fonction d'activation de l'unité linéaire rectifiée (ReLU) a la forme suivante :
f(x) = max(0, x)
Le seuil d'entrée est fixé à zéro, ce qui renvoie 0 pour les valeurs négatives et l'entrée elle-même pour les valeurs positives.
Pour les entrées supérieures à 0, la ReLU agit comme une fonction linéaire avec un gradient de 1. Cela signifie qu'il ne modifie pas l'échelle des entrées positives et permet au gradient de passer sans changement pendant la rétropropagation. Cette propriété est essentielle pour atténuer le problème du gradient de fuite.
Même si la ReLU est linéaire pour la moitié de son espace d'entrée, il s'agit techniquement d'une fonction non linéaire car elle possède un point non différentiable à x=0, où elle change brusquement de x. Cette non-linéarité permet aux réseaux neuronaux d'apprendre des modèles complexes
Étant donné que la ReLU produit un résultat nul pour toutes les entrées négatives, elle conduit naturellement à des activations éparses ; à tout moment, seul un sous-ensemble de neurones est activé, ce qui permet d'améliorer l'efficacité des calculs.
La fonction ReLU est peu coûteuse en termes de calcul car elle implique un simple seuillage à zéro. Cela permet aux réseaux de s'étendre à de nombreuses couches sans augmentation significative de la charge de calcul, par rapport à des fonctions plus complexes telles que tanh ou sigmoïde.
Activation du Softmax
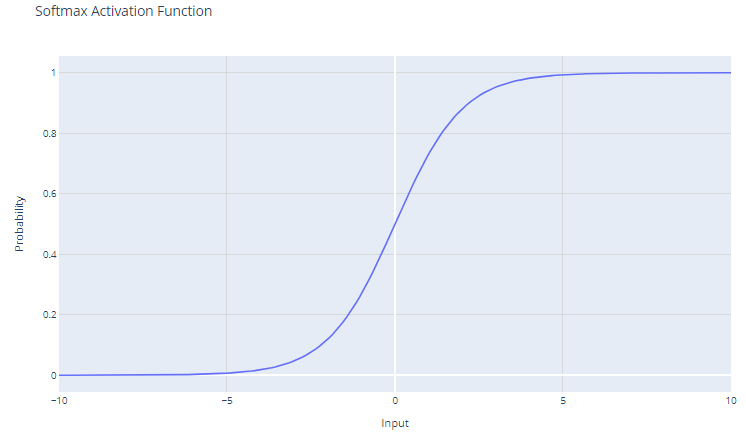
Fonction d'activation Softmax. Image par l'auteur
La fonction d'activation softmax, également connue sous le nom de fonction exponentielle normalisée, est particulièrement utile dans le contexte des problèmes de classification multi-classes. Cette fonction opère sur un vecteur, souvent appelé logit, qui représente les prédictions brutes ou les scores pour chaque classe calculés par les couches précédentes d'un réseau neuronal.
Pour un vecteur d'entrée x avec des éléments x1, x2, ..., xC, la fonction softmax est définie comme suit :
f(xi) = e^xi / Σj e^xj
La sortie de la fonction softmax est une distribution de probabilité dont la somme est égale à un. Chaque élément de la sortie représente la probabilité que l'entrée appartienne à une classe particulière.
L'utilisation de la fonction exponentielle garantit que toutes les valeurs de sortie sont non négatives. Ce point est crucial car les probabilités ne peuvent pas être négatives.
Softmax amplifie les différences dans le vecteur d'entrée. Même de petites différences dans les valeurs d'entrée peuvent entraîner des différences substantielles dans les probabilités de sortie, la ou les valeurs d'entrée les plus élevées ayant tendance à dominer dans la distribution de probabilités résultante.
Le Softmax est généralement utilisé dans la couche de sortie d'un réseau neuronal lorsque la tâche consiste à classer une entrée dans l'une de plusieurs (plus de deux) catégories possibles (classification multi-classes).
Les probabilités produites par la fonction softmax peuvent être interprétées comme des scores de confiance pour chaque classe, ce qui donne une idée de la certitude du modèle quant à ses prédictions.
Étant donné que softmax amplifie les différences, il peut être sensible aux valeurs aberrantes ou extrêmes. Par exemple, si le vecteur d'entrée a une valeur très élevée, softmax peut "écraser" les probabilités des autres classes, ce qui conduit à un modèle trop confiant.
Choisir la bonne fonction d'activation
Le choix de la fonction d'activation dépend du type de problème que vous essayez de résoudre. Voici quelques lignes directrices :
Pour la classification binaire
Utilisez la fonction d'activation sigmoïde dans la couche de sortie. Il produira des résultats entre 0 et 1, représentant les probabilités pour les deux classes.
Pour la classification multi-classes
Utilisez la fonction d'activation softmax dans la couche de sortie. Il produira des distributions de probabilités pour toutes les classes.
En cas de doute
Utilisez la fonction d'activation ReLU dans les couches cachées. ReLU est la fonction d'activation par défaut la plus courante et constitue généralement un bon choix.
Conclusion
Nous avons exploré le rôle central que jouent les fonctions d'activation dans l'apprentissage des réseaux neuronaux. Nous avons vu qu'il ne s'agit pas de simples suppléments optionnels, mais d'éléments essentiels qui permettent aux réseaux neuronaux de capturer et de modéliser la complexité inhérente aux données du monde réel. De la simple mais efficace ReLU aux interprétations probabilistes fournies par la fonction softmax, chaque fonction d'activation a sa place et son utilité dans les différentes couches d'un réseau et dans divers domaines.
Au fur et à mesure de l'évolution des réseaux neuronaux, l'exploration des fonctions d'activation s'étendra sans aucun doute, en incluant éventuellement de nouvelles formes qui répondent aux défis spécifiques des architectures émergentes. Toutefois, les principes et les fonctions abordés dans ce blog resteront probablement au cœur de la conception des réseaux neuronaux dans un avenir proche.
La sélection minutieuse des fonctions d'activation est un exercice d'équilibre - un mélange de compréhension scientifique et d'intuition artistique - qui peut affecter de manière significative les performances des réseaux neuronaux.
Intéressé par l'apprentissage profond avec le framework Keras ? Consultez notre cours Introduction à l'apprentissage profond avec Keras.

