Introdução às funções de ativação em redes neurais

O que são funções de ativação?

As funções de ativação são um bloco de construção integral das redes neurais que permite que elas aprendam padrões complexos nos dados. Eles transformam o sinal de entrada de um nó em uma rede neural em um sinal de saída que é então passado para a próxima camada. Sem as funções de ativação, as redes neurais ficariam restritas à modelagem apenas de relações lineares entre entradas e saídas.

As funções de ativação introduzem não linearidades, permitindo que as redes neurais aprendam mapeamentos altamente complexos entre entradas e saídas.

A escolha da função de ativação correta é fundamental para o treinamento de redes neurais que generalizam bem e fornecem previsões precisas. Nesta postagem, apresentaremos uma visão geral das funções de ativação mais comuns, suas funções e como selecionar funções de ativação adequadas para diferentes casos de uso.

Não importa se você está apenas começando na aprendizagem profunda ou se é um profissional experiente, compreender as funções de ativação em profundidade desenvolverá sua intuição e melhorará sua aplicação de redes neurais.

Representação da rede neural Fonte da imagem

Por que as funções de ativação são essenciais?

Sem as funções de ativação, as redes neurais consistiriam apenas em operações lineares, como a multiplicação de matrizes. Todas as camadas realizariam transformações lineares da entrada, e nenhuma não linearidade seria introduzida.

A maioria dos dados do mundo real não é linear. Por exemplo, as relações entre os preços dos imóveis e o tamanho, a renda e as compras, etc., não são lineares. Se as redes neurais não tivessem funções de ativação, elas não conseguiriam aprender os complexos padrões não lineares que existem nos dados do mundo real.

As funções de ativação permitem que as redes neurais aprendam essas relações não lineares, introduzindo comportamentos não lineares por meio de funções de ativação. Isso aumenta muito a flexibilidade e o poder das redes neurais para modelar dados complexos e diferenciados.

Tipos de funções de ativação

As redes neurais utilizam vários tipos de funções de ativação para introduzir não linearidades e permitir o aprendizado de padrões complexos. Cada função de ativação tem suas próprias propriedades exclusivas e é adequada para determinados casos de uso.

Por exemplo, a função sigmoide é ideal para problemas de classificação binária, a softmax é útil para a previsão multiclasse e a ReLU ajuda a superar o problema do gradiente de desaparecimento.

O uso da função de ativação correta para a tarefa leva a um treinamento mais rápido e a um melhor desempenho.

Vamos dar uma olhada em algumas das funções de ativação comuns:

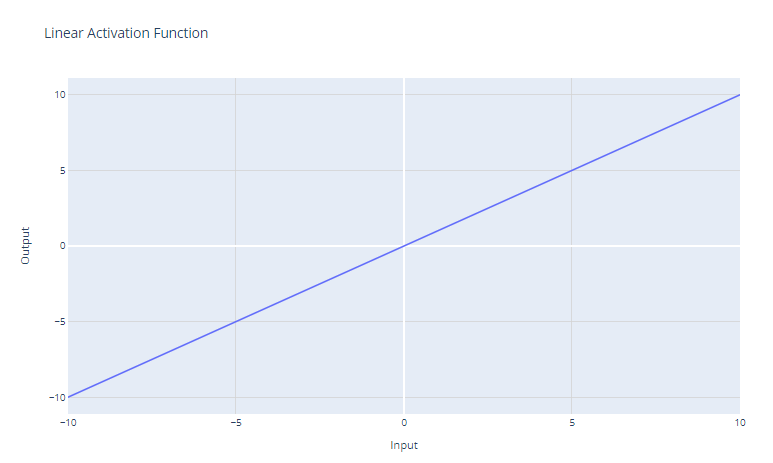
A função de ativação linear é a função de ativação mais simples, definida como:

f(x) = x

Ele simplesmente retorna a entrada x como saída. Graficamente, parece uma linha reta com uma inclinação de 1.

O principal caso de uso da função de ativação linear é na camada de saída de uma rede neural usada para regressão. Para problemas de regressão em que queremos prever um valor numérico, o uso de uma função de ativação linear na camada de saída garante que a rede neural produza um valor numérico. A função de ativação linear não esmaga nem transforma a saída, portanto, o valor real previsto é retornado.

No entanto, a função de ativação linear raramente é usada em camadas ocultas de redes neurais. Isso ocorre porque ele não oferece nenhuma não linearidade. O objetivo das camadas ocultas é aprender combinações não lineares dos recursos de entrada. O uso de uma ativação linear ao longo de todo o processo restringiria o modelo a apenas aprender transformações lineares da entrada.

Ativação do sigmoide

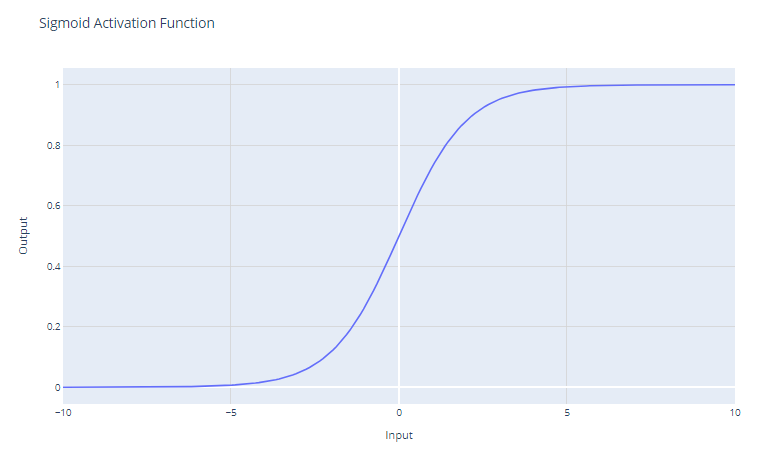
A função de ativação sigmoide, geralmente representada como σ(x), é uma função suave e continuamente diferenciável que é historicamente importante no desenvolvimento de redes neurais. A função de ativação sigmoide tem a forma matemática:

f(x) = 1 / (1 + e^-x)

Ele recebe uma entrada de valor real e a esmaga em um valor entre 0 e 1. A função sigmoide tem uma curva em forma de "S" que tem como assíntota 0 para números negativos grandes e 1 para números positivos grandes. Os resultados podem ser facilmente interpretados como probabilidades, o que o torna natural para problemas de classificação binária.

As unidades sigmoides eram populares nas primeiras redes neurais, pois o gradiente é mais forte quando a saída da unidade está próxima de 0,5, permitindo um treinamento eficiente de retropropagação. No entanto, as unidades sigmoides sofrem com o problema do "gradiente de desaparecimento" que dificulta o aprendizado em redes neurais profundas.

À medida que os valores de entrada se tornam significativamente positivos ou negativos, a função satura em 0 ou 1, com uma inclinação extremamente plana. Nessas regiões, o gradiente é muito próximo de zero. Isso resulta em alterações muito pequenas nos pesos durante a retropropagação, principalmente para os neurônios nas camadas iniciais das redes profundas, o que torna o aprendizado dolorosamente lento ou até mesmo o interrompe. Isso é conhecido como o problema do gradiente de desaparecimento em redes neurais.

O principal caso de uso da função sigmoide é como ativação para a camada de saída dos modelos de classificação binária. Ele reduz a saída a um valor de probabilidade entre 0 e 1, que pode ser interpretado como a probabilidade de a entrada pertencer a uma determinada classe.

Ativação de Tanh (tangente hiperbólica)

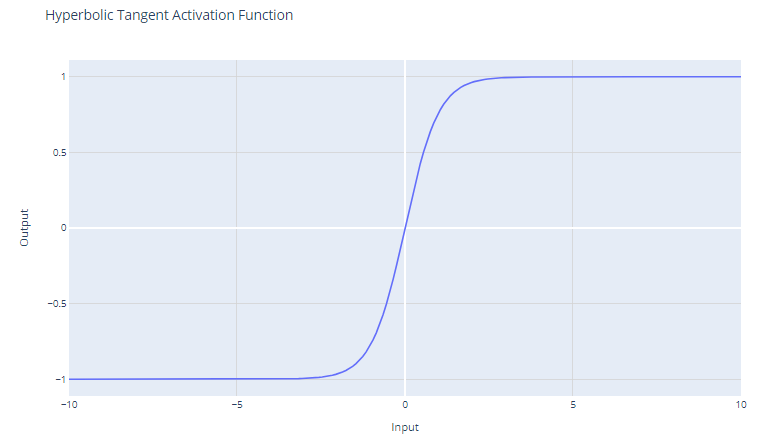
A função de ativação tanh (tangente hiperbólica) é definida como:

f(x) = (e^x - e^-x) / (e^x + e^-x)

A função tanh gera valores no intervalo de -1 a +1. Isso significa que ela pode lidar com valores negativos de forma mais eficaz do que a função sigmoide, que tem um intervalo de 0 a 1.

Ao contrário da função sigmoide, a tanh é centrada em zero, o que significa que sua saída é simétrica em torno da origem do sistema de coordenadas. Isso geralmente é considerado uma vantagem, pois pode ajudar o algoritmo de aprendizado a convergir mais rapidamente.

Como a saída de tanh varia entre -1 e +1, ela tem gradientes mais fortes do que a função sigmoide. Gradientes mais fortes geralmente resultam em aprendizado e convergência mais rápidos durante o treinamento porque tendem a ser mais resistentes ao problema de gradientes que desaparecem quando comparados aos gradientes da função sigmoide.

Apesar dessas vantagens, a função tanh ainda sofre com o problema do gradiente de desaparecimento. Durante a retropropagação, os gradientes da função tanh podem se tornar muito pequenos (próximos de zero). Essa questão é particularmente problemática para redes profundas com muitas camadas; os gradientes da função de perda podem se tornar muito pequenos para fazer alterações significativas nos pesos durante o treinamento, à medida que se propagam de volta para as camadas iniciais. Isso pode desacelerar drasticamente o processo de treinamento e levar a propriedades de convergência ruins.

A função tanh é usada com frequência nas camadas ocultas de uma rede neural. Devido à sua natureza centrada em zero, quando os dados também são normalizados para ter média zero, isso pode resultar em um treinamento mais eficiente.

Se for preciso escolher entre o sigmoide e o tanh e não houver nenhuma razão específica para preferir um em detrimento do outro, o tanh geralmente é a melhor opção devido às razões mencionadas acima. No entanto, a decisão também pode ser influenciada pelo caso de uso específico e pelo comportamento da rede durante os experimentos iniciais de treinamento.

Você pode criar uma rede neural simples do zero usando o PyTorch seguindo nosso tutorial de Kurtis Pykes ou, se for um usuário avançado, nosso curso Aprendizagem profunda com PyTorch é para você. .

Ativação da ReLU (Unidade Linear Retificada)

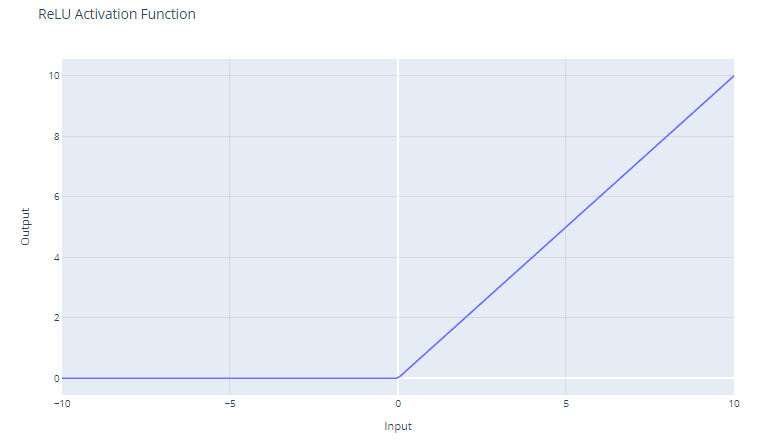
A função de ativação da Unidade Linear Retificada (ReLU) tem a forma:

f(x) = max(0, x)

Ele limita a entrada a zero, retornando 0 para valores negativos e a própria entrada para valores positivos.

Para entradas maiores que 0, o ReLU atua como uma função linear com um gradiente de 1. Isso significa que ele não altera a escala de entradas positivas e permite que o gradiente passe inalterado durante a retropropagação. Essa propriedade é fundamental para atenuar o problema do gradiente de desaparecimento.

Embora a ReLU seja linear para metade de seu espaço de entrada, ela é tecnicamente uma função não linear porque tem um ponto não diferenciável em x=0, onde muda abruptamente de x. Essa não linearidade permite que as redes neurais aprendam padrões complexos

Como o ReLU produz zero para todas as entradas negativas, ele naturalmente leva a ativações esparsas; a qualquer momento, apenas um subconjunto de neurônios é ativado, o que leva a uma computação mais eficiente.

A função ReLU é computacionalmente barata porque envolve um limiar simples em zero. Isso permite que as redes sejam dimensionadas para muitas camadas sem um aumento significativo na carga computacional, em comparação com funções mais complexas, como tanh ou sigmoide.

Ativação do Softmax

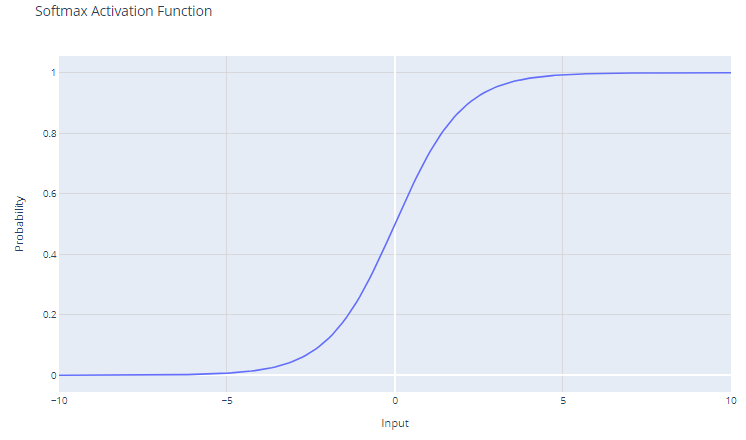
A função de ativação softmax, também conhecida como função exponencial normalizada, é particularmente útil no contexto de problemas de classificação multiclasse. Essa função opera em um vetor, geralmente chamado de logits, que representa as previsões ou pontuações brutas de cada classe calculadas pelas camadas anteriores de uma rede neural.

Para o vetor de entrada x com elementos x1, x2, ..., xC, a função softmax é definida como:

f(xi) = e^xi / Σj e^xj

A saída da função softmax é uma distribuição de probabilidade que soma um. Cada elemento da saída representa a probabilidade de a entrada pertencer a uma determinada classe.

O uso da função exponencial garante que todos os valores de saída sejam não negativos. Isso é fundamental porque as probabilidades não podem ser negativas.

O Softmax amplifica as diferenças no vetor de entrada. Mesmo pequenas diferenças nos valores de entrada podem levar a diferenças substanciais nas probabilidades de saída, com o(s) valor(es) de entrada mais alto(s) tendendo a predominar na distribuição de probabilidade resultante.

Normalmente, o Softmax é usado na camada de saída de uma rede neural quando a tarefa envolve a classificação de uma entrada em uma das várias (mais de duas) categorias possíveis (classificação multiclasse).

As probabilidades produzidas pela função softmax podem ser interpretadas como pontuações de confiança para cada classe, fornecendo informações sobre a certeza do modelo em relação às suas previsões.

Como o softmax amplifica as diferenças, ele pode ser sensível a valores extremos ou discrepantes. Por exemplo, se o vetor de entrada tiver um valor muito grande, o softmax pode "esmagar" as probabilidades de outras classes, levando a um modelo excessivamente confiante.

Escolha da função de ativação correta

A escolha da função de ativação depende do tipo de problema que você está tentando resolver. Aqui estão algumas diretrizes:

Para classificação binária:

Use a função de ativação sigmoide na camada de saída. Ele esmagará as saídas entre 0 e 1, representando as probabilidades das duas classes.

Para classificação multiclasse:

Use a função de ativação softmax na camada de saída. Ele produzirá distribuições de probabilidade em todas as classes.

Se não tiver certeza:

Use a função de ativação ReLU nas camadas ocultas. A ReLU é a função de ativação padrão mais comum e geralmente é uma boa escolha.

Conclusão

Exploramos o papel fundamental que as funções de ativação desempenham no treinamento de redes neurais. Vimos como eles não são apenas extras opcionais, mas elementos essenciais que permitem que as redes neurais capturem e modelem a complexidade inerente aos dados do mundo real. Desde a simples, porém eficaz, ReLU até as interpretações probabilísticas fornecidas pela função softmax, cada função de ativação tem seu lugar e sua finalidade em diferentes camadas de uma rede e em vários domínios de problemas.

À medida que as redes neurais continuarem a evoluir, a exploração das funções de ativação sem dúvida se expandirá, possivelmente incluindo novas formas que abordem desafios específicos de arquiteturas emergentes. No entanto, os princípios e as funções discutidos neste blog provavelmente permanecerão no centro do projeto de redes neurais em um futuro próximo.

A seleção cuidadosa das funções de ativação é um ato de equilíbrio - uma mistura de compreensão científica e intuição artística - que pode afetar significativamente o desempenho das redes neurais.

Interessado em aprender a aprendizagem profunda com a estrutura Keras? Confira nosso curso Introdução à aprendizagem profunda com Keras.