Einführung in die Maximum-Likelihood-Schätzung (MLE)

Parameter zu schätzen ist ein wichtiger Schritt in der Statistik und beim maschinellen Lernen. Unter den verschiedenen verfügbaren Methoden ist die Maximum-Likelihood-Schätzung (MLE) von aufgrund ihrer intuitiven Natur, mathematischen Genauigkeit und breiten Anwendbarkeit auf verschiedene Datentypen und Modelle einer der am häufigsten verwendeten Ansätze.

In diesem Artikel erfährst du, was MLE ist, lernst die mathematischen Grundlagen anhand detaillierter Ableitungen und Beispiele kennen und entdeckst praktische Berechnungsmethoden für die effektive Umsetzung von MLE.

Was ist die Maximum-Likelihood-Schätzung (MLE)?

Die Maximum-Likelihood-Schätzung (MLE) ist eine wichtige statistische Methode. Statistikmethode , die dazu dient, Schätzen die Parameter einer Wahrscheinlichkeitsverteilung durch die Wahrscheinlichkeitsfunktion maximiert.

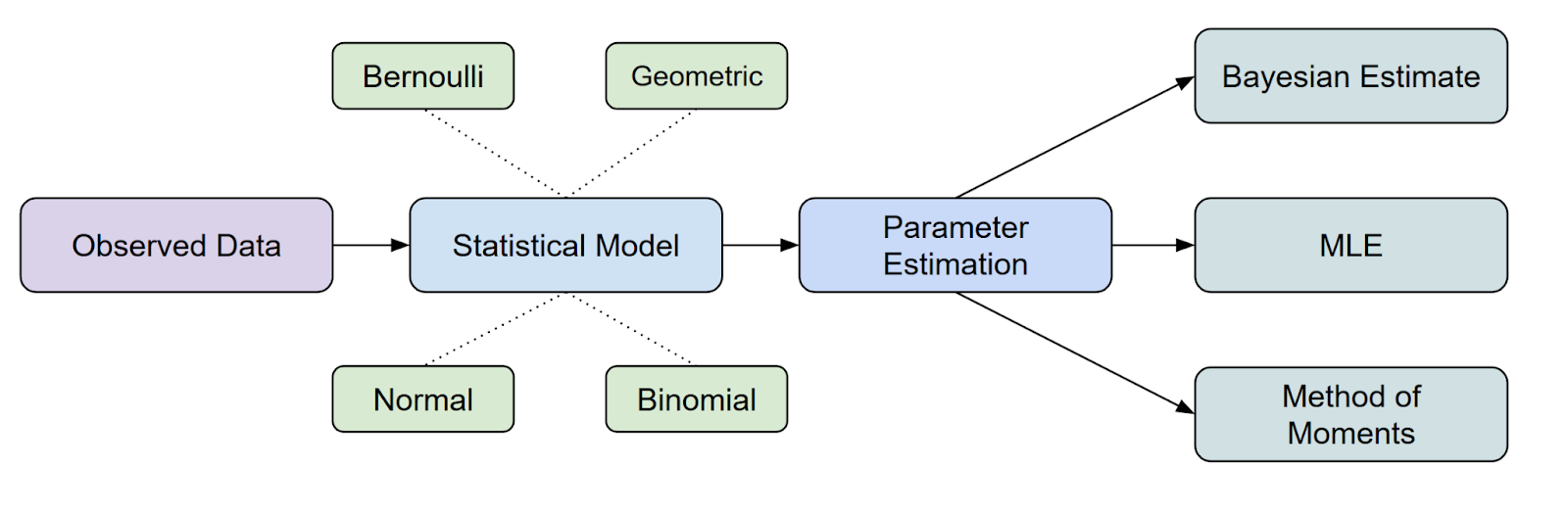
Wo passt MLE in die statistische Inferenz, ist sie eine der gängigsten Methoden, die wir zur Parameterschätzung haben.

Hier kommt vielleicht noch eine Frage auf. Was ist eine Wahrscheinlichkeitsfunktion? Lass uns das weiter besprechen.

Was ist die Wahrscheinlichkeitsfunktion?

Wir können uns die Wahrscheinlichkeitsfunktion als eine Art Maß dafür vorstellen, wie gut ein bestimmter Satz von Parametern die Daten erklärt, die du beobachtet hast.

Mit anderen Worten, es beantwortet die Frage: „Wie wahrscheinlich ist es, dass ich diese Daten mit diesen Parametern sehe?“ Aber hier gibt's ein häufiges Missverständnis zwischen Wahrscheinlichkeit und Wahrscheinlichkeit:

• Bei Wahrscheinlichkeit geht's darum, das Vorhersagen von Daten anhand von Parametern
• Der Wahrscheinlichkeits us zeigt, wie wahrscheinlich verschiedene Parameterwerte sind, wenn man die beobachteten Daten berücksichtigt. Das hängt von den Parametern für die festen Daten ab. Im Gegensatz dazu ist die Wahrscheinlichkeit eine Funktion von Daten für feste Parameter.

Zusammenfassend lässt sich also sagen, dass die Wahrscheinlichkeitsfunktion die Parameter deines Modells als Eingabe nimmt und dir eine Zahl liefert, die angibt, wie plausibel diese Parameter angesichts deiner Daten sind.

Je höher der Wert der Wahrscheinlichkeitsfunktion, desto besser erklären diese Parameter deine Daten.

Einfacher gesagt: Die Wahrscheinlichkeitsfunktion hilft uns dabei, verschiedene Parameteroptionen zu bewerten, damit wir die auswählen können, die unsere beobachteten Daten am wahrscheinlichsten machen.

Nachdem wir jetzt den Unterschied zwischen Wahrscheinlichkeit und Wahrscheinlichkeit sowie den Verwendungszweck von MLE verstanden haben, wollen wir uns mit der zugrunde liegenden Mathematik befassen.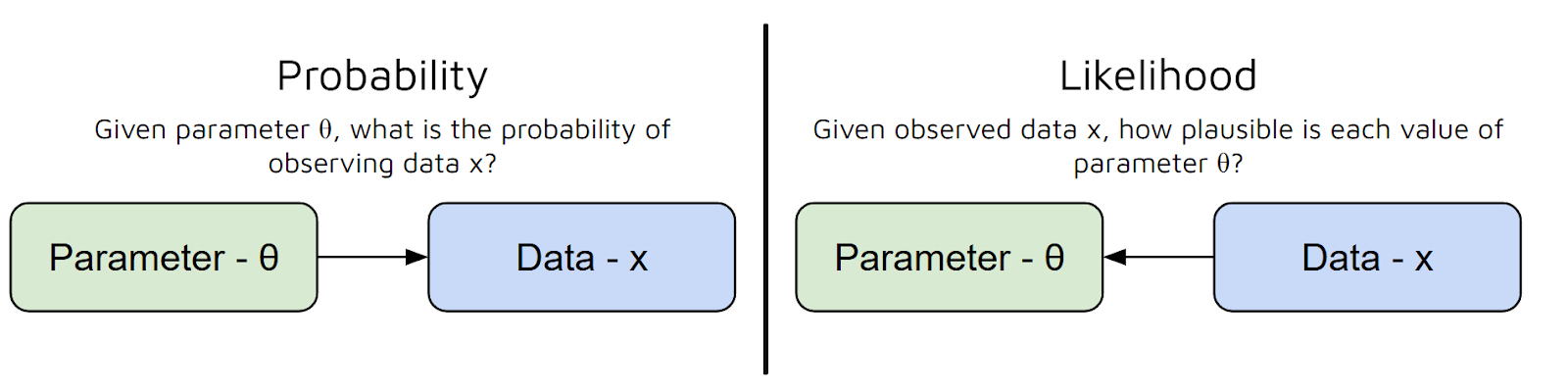

Wie man die MLE-Formel herleitet

Bevor wir uns mit konkreten Beispielen beschäftigen, schauen wir uns erst mal an, wie der Maximum-Likelihood-Schätzer (MLE) im Allgemeinen abgeleitet wird. Wir gehen jeden Schritt durch und erklären dir auch, warum wir das so machen.

Schritt 1: Wahrscheinlichkeitsmodell festlegen

Nehmen wir mal an, wir haben einen Datensatz: x₁, x₂, ..., xₙ. Wir denken, dass diese Datenpunkte aus einer Wahrscheinlichkeitsverteilung kommen, die von einem unbekannten Parameter θ (Theta) abhängt. Unser Hauptziel ist es, θ zu schätzen. 

Wenn es in unserem Datensatz zum Beispiel um Münzwürfe geht, könnte θ die Wahrscheinlichkeit für Kopf sein. Wenn der Datensatz durchgehend wäre, wie die Körpergrößen der Schüler in der Klasse, könnte θ der Mittelwert einer Normalverteilung sein.

Schritt 2: Schreiben der Wahrscheinlichkeitsfunktion

Die Wahrscheinlichkeitsfunktion zeigt, wie wahrscheinlich es ist, dass deine Daten für verschiedene Werte von θ beobachtet werden. Es wird definiert als:

Intuitiv fragen wir uns: Wenn der Parameter θ einen bestimmten Wert annimmt, wie hoch ist die Wahrscheinlichkeit, dass wir genau diesen Datensatz sehen? 

Dieser Datensatz wird als gemeinsame Wahrscheinlichkeit der Beobachtung der einzelnen Datenpunkte (x₁, x₂, ..., xₙ) dargestellt, vorausgesetzt, dass sie unter dem durch θ parametrisierten Modell generiert wurden.

Mit der Kettenregel der Wahrscheinlichkeitkönnen wir die obige Gleichung wie folgt aufschlüsseln:

Das ist allerdings eine ziemlich komplizierte Gleichung! Wir gehen also davon aus, dass die Datenpunktevoneinander unabhängig sind – genauer gesagt, bedingt unabhängig.

Auf diese Weise erhalten wir die gemeinsame Wahrscheinlichkeit als Produkt der einzelnen Wahrscheinlichkeiten:

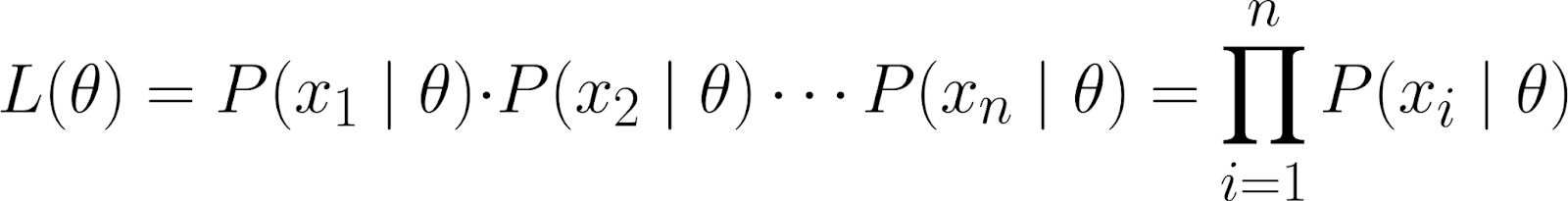
Da unsere beobachteten Datenpunkte von θ bedingt unabhängig, wissen wir, dass die folgende Gleichung stimmt:

Das liegt daran, dass wir angenommen haben, dass die Datenpunkte x₁ und x₂ bedingt unabhängig sind, sobald wir den Wert von θ kennen.

Schritt 3: Finde den Wert von θ, der die Wahrscheinlichkeit maximiert.

Wir sind in der Situation, dass wir die Werte von θ finden müssen, die die Wahrscheinlichkeitsfunktion maximierenmaximiert (d. h. die beobachteten Daten am wahrscheinlichsten macht):

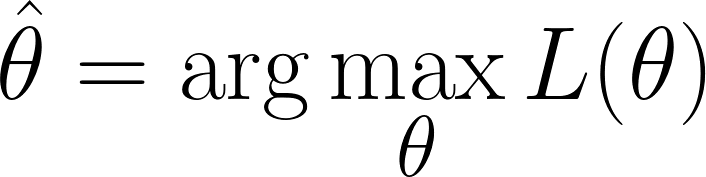
Denk aber dran, dass unsere Wahrscheinlichkeitsfunktion ein Produkt enthält. Die Arbeit mit Produkten kann chaotisch werden, vor allem wenn es um viele Datenpunkte geht. Um es einfacher zu machen, nehmen wir denLogarithmus der Wahrscheinlichkeitsfunktion nach , weil das das Produkt in eine Summe umwandelt.

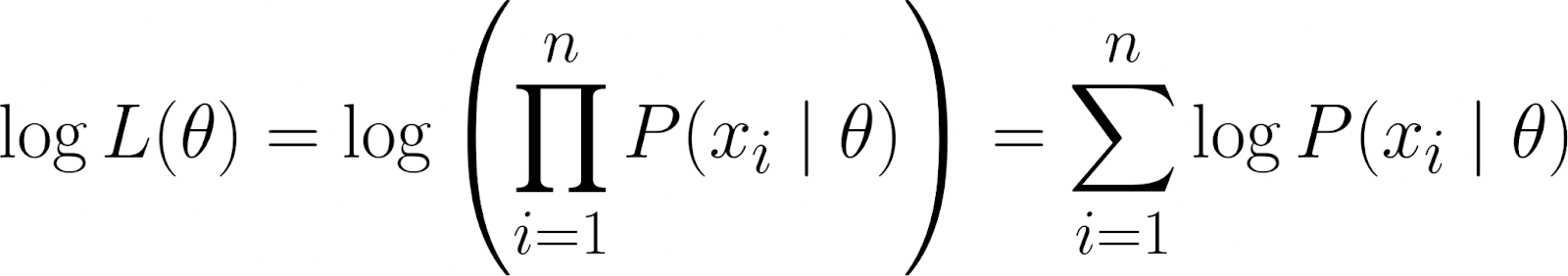
TDas gibt uns die log-Wahrscheinlichkeit, die ein paar nützliche Eigenschaften hat:

• Der Log macht aus Produkten Summen, mit denen man viel besser arbeiten kann, vor allem beim Differenzieren.
• Die Logarithmusfunktion ist monoton, also gibt das Maximieren der Log-Likelihood dasselbe θ wie das Maximieren der Likelihood.

Schritt 4: Den besten Wert finden

Wir sind jetzt an einem Punkt, wo wir unterscheiden können, aber beim maschinellen Lernen wollen wir meistens, dass unsere Verlustfunktionen minimiert werden. Zum Glück ist das ganz einfach zu beheben. 

Durch das Minuszeichen (also mal -1) am Anfang unserer Funktion müssen wir jetzt minimieren unsere Verlustfunktion minimieren, die jetzt als Negative Log-Likelihood-Verlustfunktion

Jetzt können wir mit Hilfe der Infinitesimalrechnung den Wert von θ berechnen. Indem man die Ableitung der Log-Likelihood nach θ nimmt, sie auf Null setzt und nach θ auflöst. Das liegt daran, dass das Minimum einer Funktion dort auftritt, wo ihre Ableitung null ist (und die zweite Ableitung positiv ist).

Deshalb lautet die endgültige Gleichung für MLE:

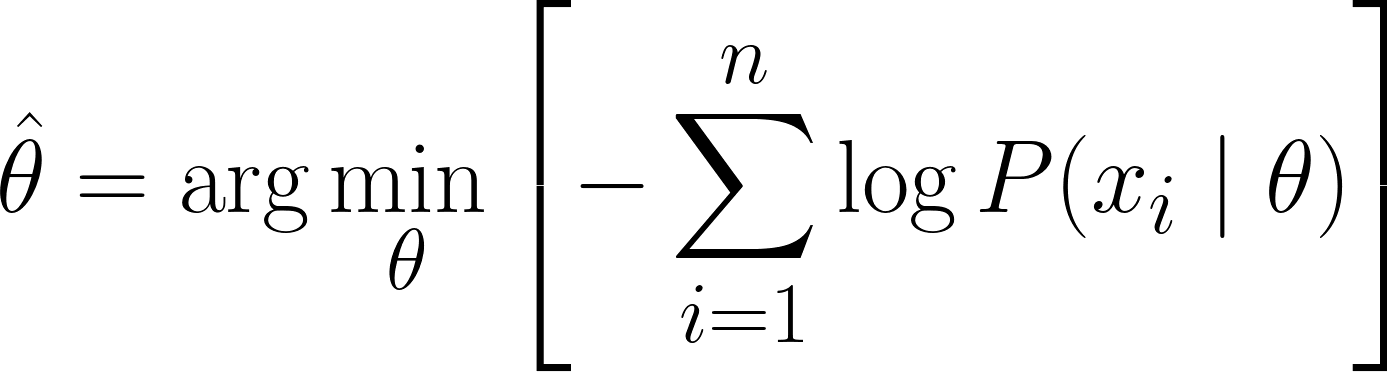
Beispiele für MLE

Da wir die MLE-Gleichung erfolgreich abgeleitet haben, schauen wir uns ein paar Beispiele an, um unser Verständnis zu festigen.

Beispiel für Würfelwürfe

Fangen wir mit einem einfachen Beispiel an: Schätzen wir mal, wie hoch die Chance ist, mit einem vielleicht nicht ganz fairen Würfel eine Sechs zu würfeln.

Angenommen, wir würfeln 12 Mal mit einem Würfel und schreiben die Ergebnisse auf:. Wir wollen diese Daten mit einerbinomialen Kategoriale Verteilung ( ) modellieren, aber konzentrieren wir uns erst mal auf die Schätzung der Wahrscheinlichkeit θ (Theta), dass eine Sechs gewürfelt wird. In diesem Beispiel:

• Parameter (θ): Der Wert, den du schätzen willst – Wahrscheinlichkeit, eine Sechs zu würfeln
• Daten (x): Die Ergebnisse, die wir gesehen haben – 4 Sechsen bei 12 Würfen

Jetzt rechnen wir die Wahrscheinlichkeitsfunktion aus, die wir, weil wir bei 12 Würfen 4 Sechsen gewürfelt haben, wie folgt erhalten:

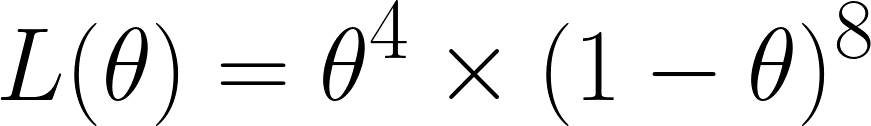
Wir haben das so rausbekommen, weil wir von den 12 Versuchen 4 Mal eine 6 gewürfelt haben – also haben wir θ⁴ – und 8 Mal keine 6 gewürfelt haben – also haben wir den Term (1 - θ)⁸. 

Erinnert euch, wir haben multipliziert , weil wir angenommen haben, dass sie bedingt unabhängig sind.

Jetzt nehmen wir die negative Log-Likelihood , wie wir es vorher besprochen haben, und erhalten diese Gleichung:

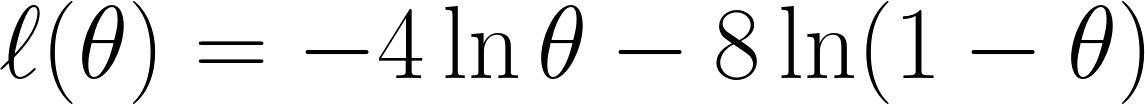
Schließlich differenzieren wir die Gleichung mit nach θ und setzen sie gleich 0 (da wir den Minimalpunkt suchen wollen):

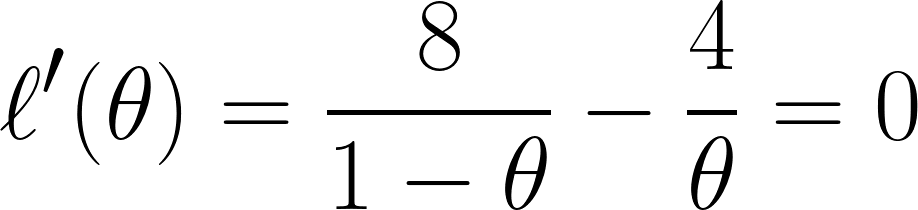
Und mit dieser Gleichung können wir sagen, dass θ gleich ⅓ ist. 

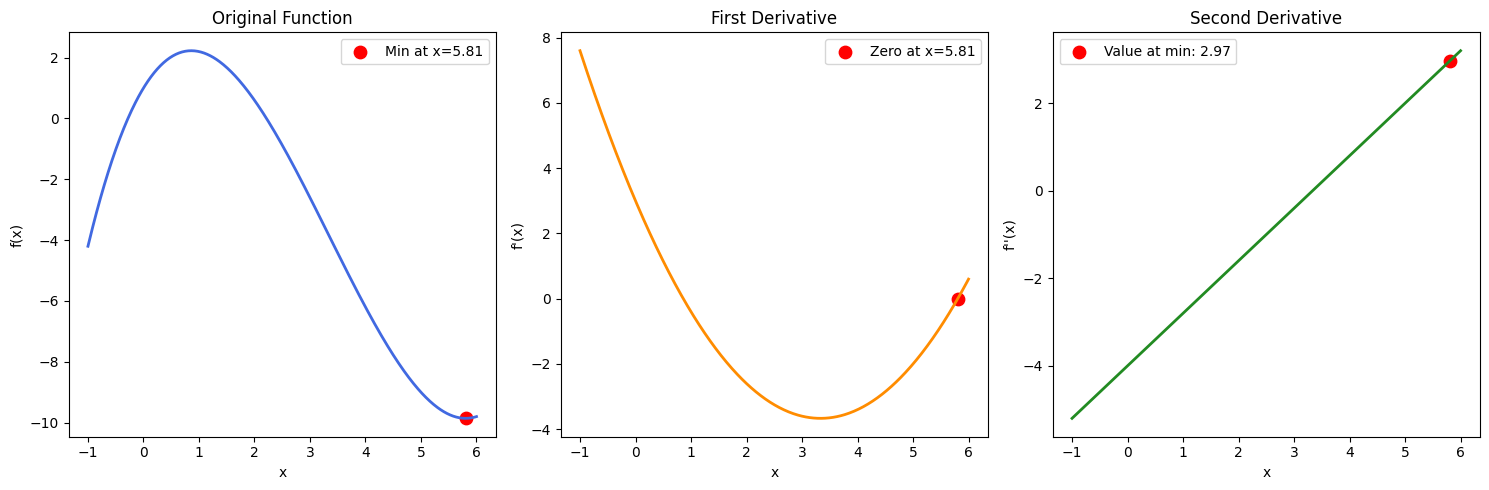
Hinweis: Wenn wir mehrere Lösungen für θ gefunden hätten, müssten wir auch die zweite Ableitung berechnen und schauen, welche θ-Werte ein positives Ergebnis liefern (um sicherzugehen, dass wir einen Minimalpunkt gefunden haben). Das kannst du mit einer Beispielfunktion in der Abbildung unten checken:

Beispiel für Höhen

Schauen wir uns jetzt ein Beispiel an, wo wir den Mittelwert einer normalen (Gaußschen) Verteilung schätzen wollen.

Nehmen wir mal an, wir haben einen Datensatz mit den Körpergrößen von 5 Leuten: 160, 165, 170, 175, 180 (in cm). Wir nehmen auch an, dass diese aus einer Normalverteilung mitunbekannter Mittelwertfunktion μ (mu) und bekannter Varianz σ² (sagen wir mal σ² = 25, um es einfach zu halten) stammen.

• Parameter (μ): Der Wert, den du schätzen willst (die durchschnittliche Höhe)
• Data (x₁, x₂, ..., x₅): Die gemessenen Höhen

Die Wahrscheinlichkeitsfunktion für die Normalverteilung (mit bekannter Varianz) ist. 

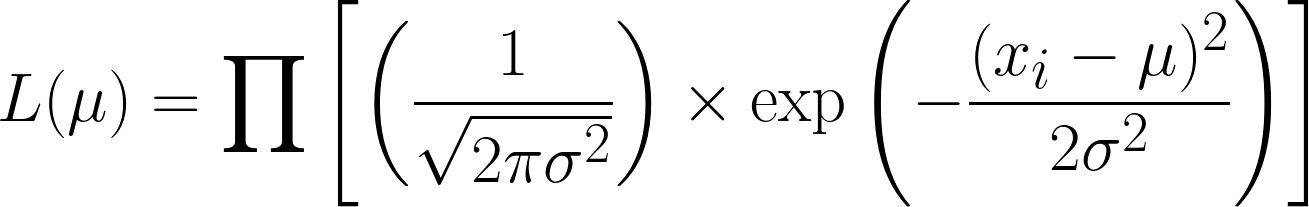
Das ist echt kompliziert, aber wenn man den negativen Logarithmus nimmt, wird es einfacher. Hoffentlich kannst du jetzt sehen, wie nützlich die Logarithmusfunktion in unserer Gleichung ist. Die Gleichung, die wir kriegen, sieht so aus:

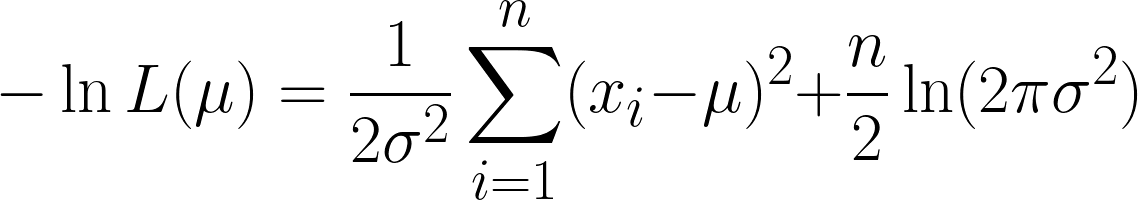
Wir kriegen hier zwei Ausdrücke, aber pass auf, dass wir den zweiten Ausdruck bei der Ableitung nicht beachten müssen, weil wir nach μund der zweite Term kein μ enthält.

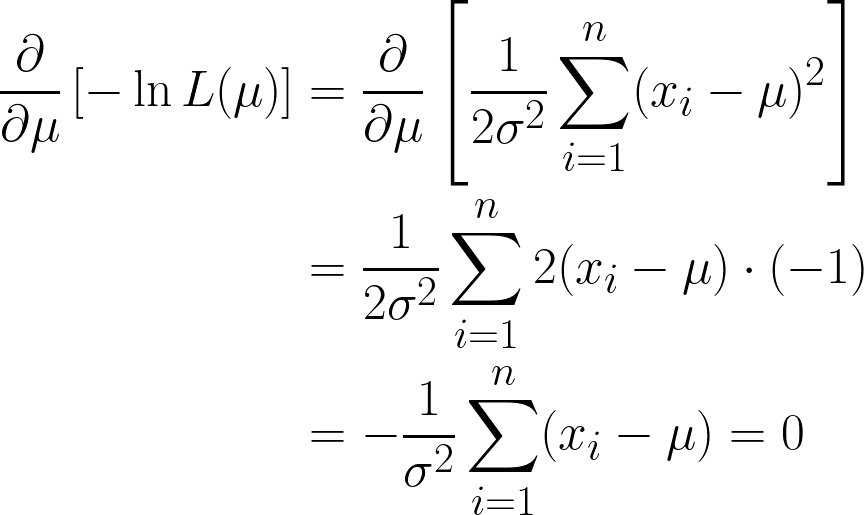
Wir sind fast fertig, aber schau dir mal μ in den Klammern an. 

Da es sich um eine Konstante, können wir sie einfach mit n multiplizieren, da die n-fache Addition von μ einfach n*μ ergibt.

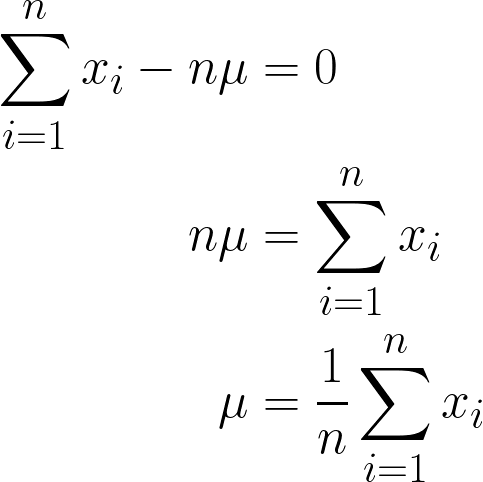
Die endgültige Antwort, die wir erhalten haben, sollte intuitiv einleuchtend sein, da sie mathematisch so formuliert ist, dass alle Werte von x addiert und durch n (die Anzahl der Beobachtungen, die wir haben) geteilt werden, und dies ist auch die Definition des Mittelwerts!

Wenn wir also unsere Datenwerte in diese Gleichung einsetzen, erhalten wir einen Mittelwert von 170 cm. 

Um das besser zu zeigen, hier eine Animation, die zeigt, wie sich die Wahrscheinlichkeit ändert, wenn wir μ ändern:

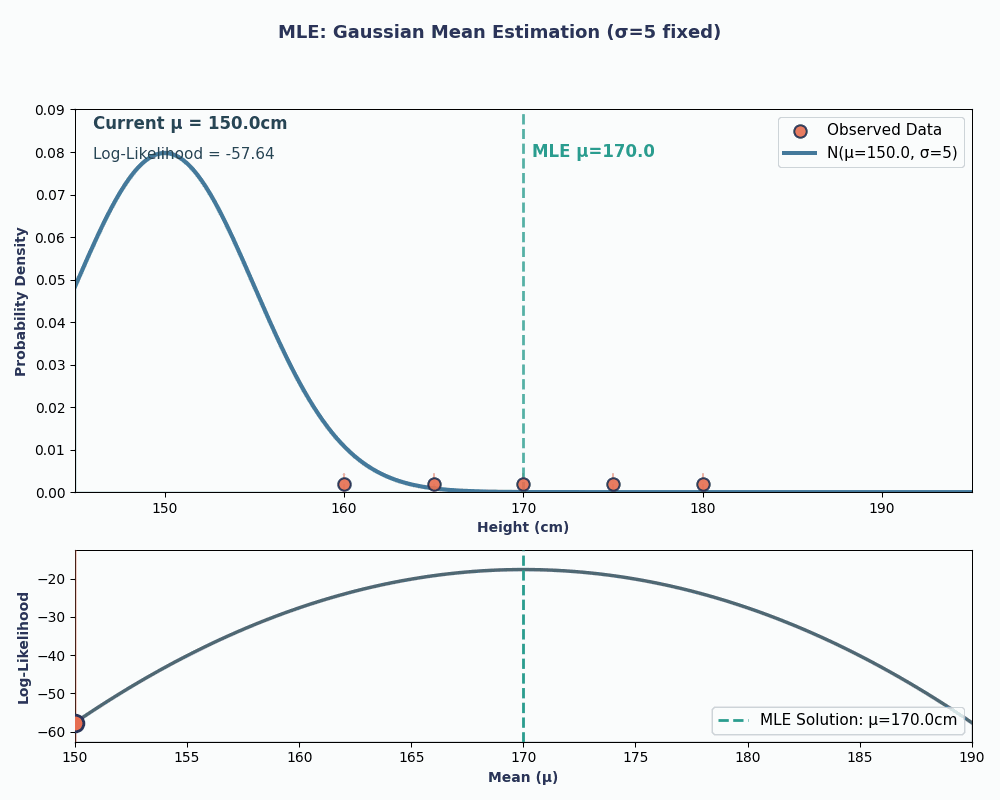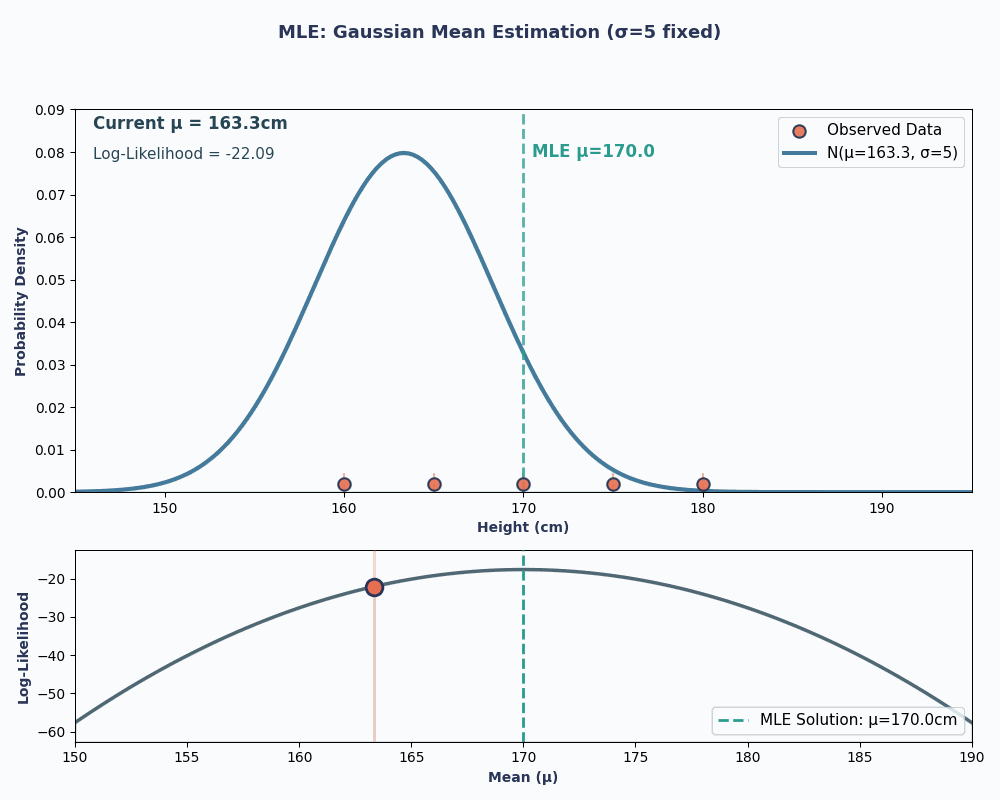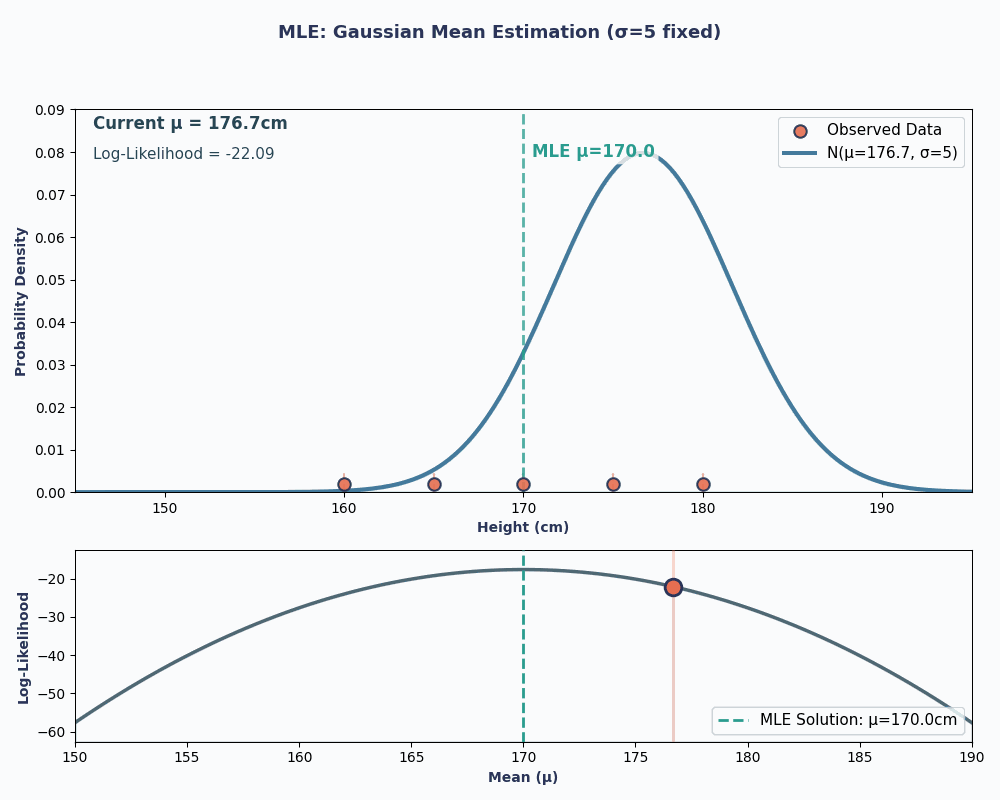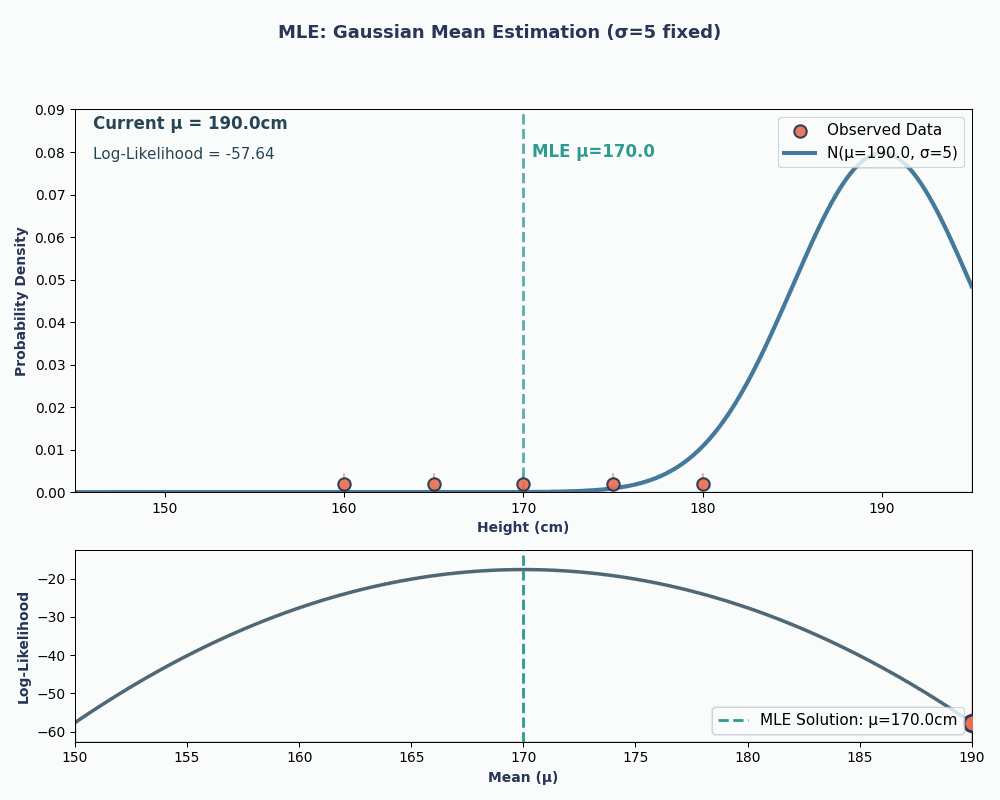
In beiden Beispielen hat uns die Verwendung von MLE den Parameterwert geliefert, der unsere beobachteten Daten unter dem gewählten Modell am wahrscheinlichsten macht. Natürlich kann MLEauch mitmehreren Parameterwerten arbeiten,die wir über„ “ übergeben, auch wenn die Berechnung dann etwas länger dauert!

Codierung MLE

Nachdem wir nun die zugrunde liegende Struktur von MLE verstanden haben, wollen wir uns ansehen, wie man dies in Python programmiert. Wir werden die Lösung aus dem vorherigen Beispiel (Höhen) programmieren. 

# Importing libraries 
import numpy as np # used for handling arrays and mathematical operations.
from scipy.optimize import minimize # function that minimizes another function

# This is our sample data 
data = np.array([160, 165, 170, 175, 180])

# This was the variance we had assumed before
sigma_squared = 25

# Negative Log-Likelihood function
def negative_log_likelihood(mu):
    n = len(data) # Number of data points
    return 0.5 * n * np.log(2 * np.pi * sigma_squared) + \
           np.sum((data - mu)**2) / (2 * sigma_squared) # The NLL is for the Univariate Gaussian Distribution

# Optimizing the NLL
result = minimize(negative_log_likelihood, x0=170)  # initial guess

# Our final estimated mean
estimated_mu = result.x[0]
print(f"MLE estimate of mu: {estimated_mu}")

Rechenstrategien und Algorithmen

Schau mal, als wir das letzte Beispiel programmiert haben, haben wir eine Funktion namens „ negative_log_likelihood() ” erstellt, die die Hauptlogik für die Berechnung des MLE einer univariaten Gaußschen Verteilung enthält .

Einerseits könnte man sagen, dass wir diese Gleichung letztendlich fest programmiert haben und die scipy.optimize verwendet haben, um diese Funktion zu minimieren. Natürlich ist das immer noch eine super Lösung, weil die Gaußsche Verteilung eine geschlossene Lösung hat. 

Schauen wir uns mal andere Methoden an, um Lösungen für MLE zu berechnen.

Geschlossene Lösungen und wann sie funktionieren

Wie oben besprochen, können wir in einigen glücklichen Fällen die MLE-Gleichungen analytischlösen , was bedeutet, dass wir eine exakte Formel für die Parameterschätzungen ableiten können. Diese werden alsgeschlossene Lösungen für „ “ bezeichnet und sind oft einfach, intuitiv und schnell zu programmieren und zu berechnen.

Jetzt ist es wichtig zu fragen, wann es geschlossene Lösungen gibt.

1. Wenn die Log-Likelihood-Funktion differenzierbar, konkav und algebraisch berechenbar ist.
2. Wenn das Modell einfach genug, also normalerweise nur ein oder zwei Parameter hat und keine versteckten Variablen.

Numerische Optimierungstechniken

Für kompliziertere Modelle gibt's keine analytischen Lösungen oder sie sind echt kompliziert zu berechnen. In solchen Fällen nutzen wirnumerische Optimierungsmethoden aus dem Bereich der „ “ ( ) – das sind iterative Algorithmen, die nach Parametern suchen, die die Log-Likelihood maximieren. Lass uns das kurz erklären:

1. Newton-Raphson-Methode: Diese Methode nutzt beides:

• Die erste Ableitung (Gradient) zur Bestimmung der Steigung und
• Die zweite Ableitung (Hessesches) wird verwendet, um die Krümmung zu messen und die Schrittweite entsprechend anzupassen.
• Die Aktualisierungsregel lautet wie folgt:
• Der größte Vorteil ist, dass es schnell in die Nähe des Optimums konvergiert nahe am Optimum.
• Allerdings muss man dafür zweite Ableitungen berechnen, die manchmal ziemlich instabil oder aufwändig in hohen Dimensionen

2. Quasi-Newton-Methoden (z. B. BFGS):

• Schätze die Hesse-Matrix nur mit der ersten Ableitung.
• Verwendet in beliebten Bibliotheken wie scipy.optimize.minimize in Python (mit BFGS als Standard).
• Mehr numerisch stabil und vielseitiger einsetzbar als Newton-Raphson.

3. Erwartungsmaximierungsalgorithmus (EM):

• Spezielle Optimierungstechnik, die verwendet wird, wenn die Daten latente (versteckte) Variablen enthalten. latente (versteckte) Variablen– Werte, die wir nicht direkt sehen können, die aber die Daten beeinflussen.
• Dieser Algorithmus besteht aus zwei Schritten:
• E-Schritt (Erwartung): Berechne den erwarteten Wert der Log-Likelihood mit den aktuellen Schätzungen der Parameter und den beobachteten Daten.
• M-Schritt (Maximierung): Maximiere diese erwartete Log-Likelihood, um die Parameterschätzungen zu aktualisieren.

Eigenschaften von MLE

Aus unseren Beispielen und Berechnungen geht klar raus, dass MLE nützlich ist. Genau genommen hat MLE die folgenden Eigenschaften: 

1. Konsistenz: Mit zunehmender Stichprobengröße nähert sich der MLE dem wahren Wert des Parameters an.
2. Asymptotische Normalität: Bei großen Stichproben wird die Verteilung des MLE ungefähr normal (glockenförmig) um den wahren Parameterwert herum. Das ist die Basis, um Konfidenzintervalle zu bilden.
3. Effizienz: Unter allen unvoreingenommenen Schätzern hat der MLE die geringstmögliche Varianz (er erreicht zumindest asymptotisch die Cramér-Rao-Untergrenze).
4. Invarianz: Wenn θ̂ der MLE für θ ist, dann ist für jede Funktion g, g(θ̂) der MLE für g(θ). Mit anderen Worten: MLEs bleiben bei Transformationen erhalten.

Es gibt aber auch Fälle, wo MLE vielleicht nicht die beste Wahl ist:

1. Kleine Proben: MLE kann verzerrt sein, wenn die Stichprobengröße klein ist. Zum Beispiel unterschätzt der MLE für die Varianz (σ̂²) oft die wahre Varianz (σ²).
2. Robustheit: MLE reagiert empfindlich auf Ausreißer und falsche Modellspezifikationen. Alternativen wie M-Schätzer können robustere Schätzungen liefern.
3. Bayesianische Alternative: Die Maximum-A-Posteriori-Schätzung (MAP) kombiniert Vorwissen mit der Wahrscheinlichkeit und bietet so eine Bayes'sche Perspektive und manchmal stabilere Schätzungen, vor allem bei begrenzten Daten.

Anwendungen in der statistischen Modellierung

In diesem Abschnitt schauen wir uns an, wo MLE beim maschinellen Lernen und in der KI tatsächlich eingesetzt wird.

Regression und Klassifizierung

Einer der wichtigsten Bereiche, in denen MLE zum Einsatz kommt, ist die logistische Regression. Hier schätzen wir die Wahrscheinlichkeit, dass ein Ergebnis zu einer bestimmten Klasse gehört (z. B. Kundenabwanderung). Dazu passen wir Parameter andas Modell an, um die Wahrscheinlichkeit der beobachteten Ergebnissezu maximieren .

Selbst bei linearen Regressionist die Lösung der kleinsten Quadrate tatsächlich auch die MLE, wenn wir normalverteilte Fehler annehmen.

Hypothesentests und Modellauswahl

MLE kann auch zum Vergleichen von Modellen verwendet werden. 

Der Likelihood-Ratio-Test (LRT) hilft uns zum Beispiel dabei, zu checken, ob das Hinzufügen zusätzlicher Variablen zu einem Modell dessen Leistung deutlich verbessert. Es vergleicht die Wahrscheinlichkeit von zwei Modellen: einem einfacheren (Nullmodell) und einem komplexeren (Alternativmodell).

Wir haben auch das Akaike-Informationskriterium (AIC), das Komplexität bestraft, um Überanpassung zu vermeiden. Diese Tools sind in Bereichen wie Finanzen, Medizin und Marketing weit verbreitet.

Einschränkungen und Alternativen zu MLE

Obwohl es leistungsstark ist, hat es auch Nachteile. Schauen wir mal kurz, wo es Probleme gibt und was wir stattdessen nehmen können.

Wichtigste Einschränkungen von MLE

• Empfindlich gegenüber Modellfehlspezifikationen: Wenn unser Modell falsch ist (z. B. wenn wir eine Normalverteilung für schiefe Daten verwenden), liefert uns MLE irreführende Ergebnisse.
• Ausreißerempfindlichkeit: Ein paar falsche Daten können deine Schätzungen total durcheinanderbringen.
• Rechenaufwand: Bei großen Modellen, vor allem mit vielen Parametern oder Einschränkungen, kann die Optimierung der Wahrscheinlichkeit langsam oder instabil sein.
• Mehrere Lösungen: Manchmal hat die Wahrscheinlichkeitsfläche mehrere Spitzen (lokale Maxima), was die Suche nach der besten Lösung schwierig macht.

Alternativen zur Maximum-Likelihood-Schätzung

Wenn MLE nicht gut funktioniert, gibt's ein paar Optionen:

• MAP (Maximum a Posteriori): Wie MLE, aber mit einer zusätzlichen Vorannahme. Das kann helfen, Schätzungen zu stabilisieren, wenn nicht so viele Daten da sind.
• Momentmethode: Vergleicht Messwerte (wie den Mittelwert oder die Varianz) mit theoretischen Werten. Es ist zwar nicht so genau wie MLE, aber dafür echt einfach zu berechnen.
• Kleinste Quadrate: Bei linearen Regressionen mit Gaußschen Fehlern sind die Methode der kleinsten Quadrate und die MLE dasselbe. Aber die Methode der kleinsten Quadrate kann immer noch nützlich sein, wenn die MLE zu kompliziert ist.

Verschiedene Methoden funktionieren in verschiedenen Situationen besser. MLE ist vielleicht nicht immer die beste Lösung, aber oft ein guter Anfang.

Fazit

Die Maximum-Likelihood-Schätzung ist eine der natürlichsten und am häufigsten verwendeten Methoden zur Parameterschätzung. Das Ziel ist, die beobachteten Datenso wahrscheinlich wie möglich zu machen( ) , damit sie in vielen verschiedenen Szenarien verwendet werden können, wie zum Beispiel beim Werfen einer Münze, bei Gaußschen Höhenverteilungen usw.

MLE passt sich an verschiedene Modelle an und lässt sich mit Daten skalieren, sodass es sowohl mathematisch elegant als auch praktisch leistungsstark ist. Obwohl es seine Nachteile hat, vor allem bei kleinen oder unübersichtlichen Datensätzen, bleibt es ein grundlegendes Werkzeug beim Lernen vonmaschinellem Lernen und KI mit „ “.

Wenn du dich für maschinelles Lernen interessierst, schau dir unbedingt unseren Lernpfad „Machine Learning Scientist in Python“ an, der sich mit überwachtem, unüberwachtem und Deep Learning beschäftigt. 

Bist du bereit, dein Wissen über die Maximum-Likelihood-Schätzung mit praktischen Übungen zu vertiefen? Diese Ressourcen können dir dabei helfen, dein Wissen anzuwenden und praktische Erfahrungen zu sammeln:

• Wahrscheinlichkeit maximieren, Teil 1 (Python): Berechne und zeig die Log-Likelihoods, um zu sehen, wie Parameterwerte in der Praxis ermittelt werden.
• OLS-Regression: Die wichtigsten Ideen erklärt: Schau dir mal an, wie die Regression der kleinsten quadratischen Abweichungen und die MLE zusammenhängen, wenn man von Gaußschen Fehlern ausgeht, und festige dabei die wichtigsten statistischen Konzepte.
• Logistische Regression in Python verstehen: Schau dir an, wie logistische Regression MLE für eine effektive Klassifizierung und Parameterschätzung nutzt.