Introdução à Estimativa de Máxima Verossimilhança (MLE)

A estimativa de parâmetros é uma etapa fundamental na análise estatística e no machine learning. Entre os vários métodos disponíveis,a Estimativa de Máxima Verossimilhança (MLE) de é uma das abordagens mais usadas por ser intuitiva, matematicamente rigorosa e aplicável a vários tipos de dados e modelos.

Neste artigo, você vai aprender o que é MLE, explorar seus fundamentos matemáticos por meio de derivações detalhadas e exemplos, e descobrir métodos computacionais práticos para implementar MLE de forma eficaz.

O que é Estimativa de Máxima Verossimilhança (MLE)?

A estimativa de máxima verossimilhança (MLE) é um método estatístico importante método estatístico usado para estimar os parâmetros de uma distribuição de probabilidade, maximizar a função de verossimilhança.

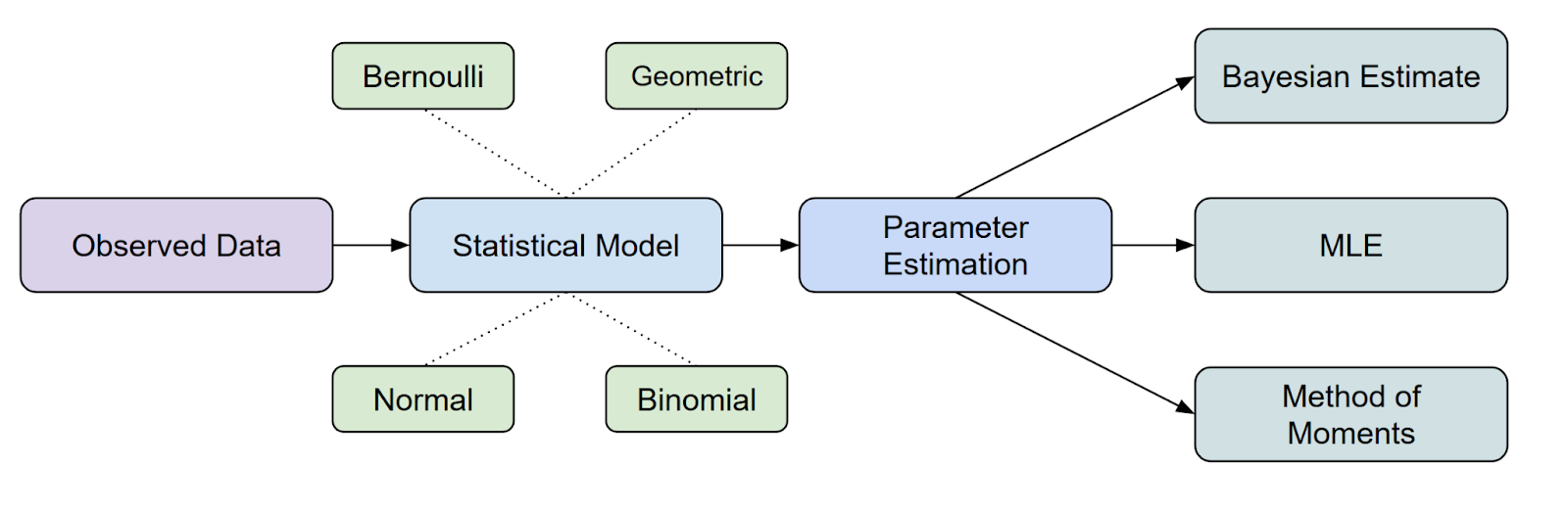
Em termos de onde o MLE se encaixa na inferência estatística, é um dos métodos mais comuns que temos para estimar parâmetros.

Mas aí você pode ter outra dúvida. O que é uma função de probabilidade? Vamos conversar mais sobre isso.

O que é a Função de Probabilidade?

A gente pode pensar na função de verossimilhança como uma forma de medir o quão bem um conjunto específico de parâmetros explica os dados que você observou.

Em outras palavras, responde à pergunta: “Com esses valores de parâmetros, qual é a chance de eu ver esses dados?” Mas tem um erro comum aqui entre Probabilidade e Possibilidade:

• Probabilidade é sobre prever dados a partir de parâmetros.
• A medida de verossimilhança ( ) mostra o quão plausíveis são diferentes valores de parâmetros, considerando os dados observados. É uma função de parâmetros para dados fixos. Já a probabilidade é uma função dos dados para parâmetros fixos.

Então, pra resumir, a função de verossimilhança pega os parâmetros do seu modelo e te dá um número que mostra o quão plausíveis esses parâmetros são, considerando os seus dados.

Quanto maior o valor da função de verossimilhança, melhor esses parâmetros explicam seus dados.

Pra simplificar ainda mais, a função de verossimilhança nos ajuda a “pontuar” diferentes opções de parâmetros, pra que a gente possa escolher aqueles que tornam nossos dados observados mais prováveis.

Agora que já entendemos a diferença entre probabilidade e verossimilhança, além de para que serve o MLE, vamos ver a matemática por trás disso.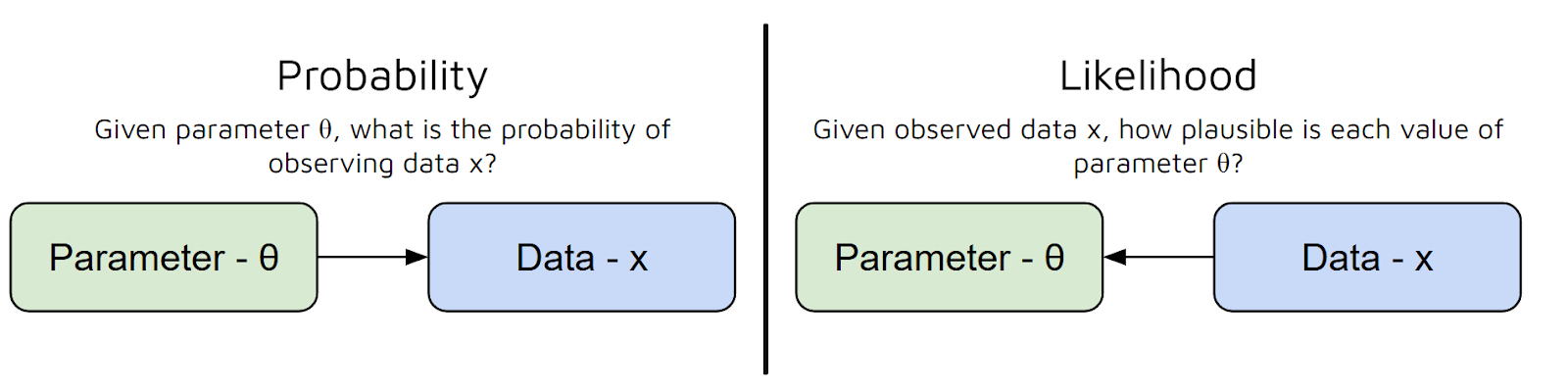

Como chegar à fórmula do MLE

Antes de entrarmos em exemplos específicos, vamos ver como o estimador de máxima verossimilhança (MLE) é derivado em geral. Vamos ver cada etapa e também explicar o porquê de cada uma delas.

Passo 1: Definir modelo de probabilidade

Digamos que temos um conjunto de dados: x₁, x₂, ..., xₙ. A gente acha que esses dados vêm de uma distribuição de probabilidade que depende de um parâmetro desconhecido chamado θ (theta). Nosso principal objetivo é estimar θ. 

Por exemplo, se nosso conjunto de dados fosse sobre jogadas de moeda, θ poderia ser a probabilidade de cair cara. Se o conjunto de dados fosse contínuo, como a altura dos alunos da turma, θ poderia ser a média de uma distribuição normal.

Passo 2: Escrevendo a função de verossimilhança

A função de verossimilhança mede a probabilidade de observar seus dados para diferentes valores de θ. É quando a gente define algo como sendo assim porque achamos que é assim.

Intuitivamente, estamos perguntando: dado que o parâmetro θ tem um valor específico, qual é a probabilidade de observar esse conjunto de dados específico? 

Esse conjunto de dados é mostrado como a probabilidade conjunta de observar os pontos de dados individuais (x₁, x₂, ..., xₙ), supondo que eles foram gerados sob o modelo parametrizado por θ.

Usando a regra da cadeia da probabilidade, podemos expandir a equação acima para:

Mas essa equação é bem complicada! Então, a gente assume que os pontos de dados sãoindependentes um do outro - mais especificamente, independentes condicionalmente.

Ao fazer isso, podemos obter a probabilidade conjunta como o produto das probabilidades individuais:

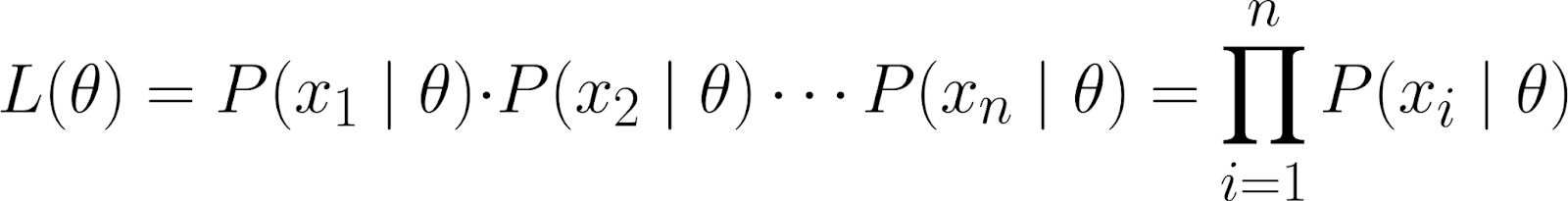
Como os pontos de dados que observamos são condicionalmente independentes de θ, sabemos que a seguinte equação é verdadeira:

Isso é porque achamos que, uma vez que sabemos o valor de θ, os pontos de dados x₁ e x₂ são condicionalmente independentes.

Passo 3: Encontre o valor de θ que maximiza a probabilidade

Estamos na posição em que precisamos encontrar os valores de θ que maximizam a função de verossimilhança(ou seja, que torna os dados observados mais prováveis):

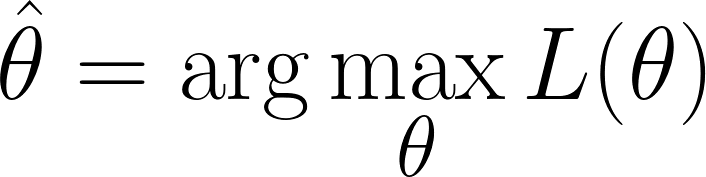
Mas, lembra que nossa função de verossimilhança tem um produto. Trabalhar com produtos pode ser complicado, principalmente quando tem muitos dados. Para simplificar, usamos ologaritmo natural ( ) da função de verossimilhança, já que isso transforma o produto em uma soma.

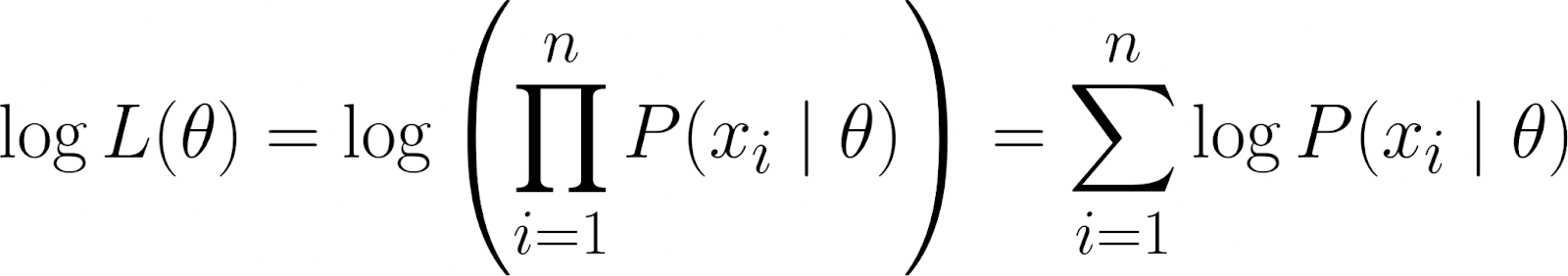
TIsso nos dá a log-verossimilhança, que tem algumas propriedades benéficas:

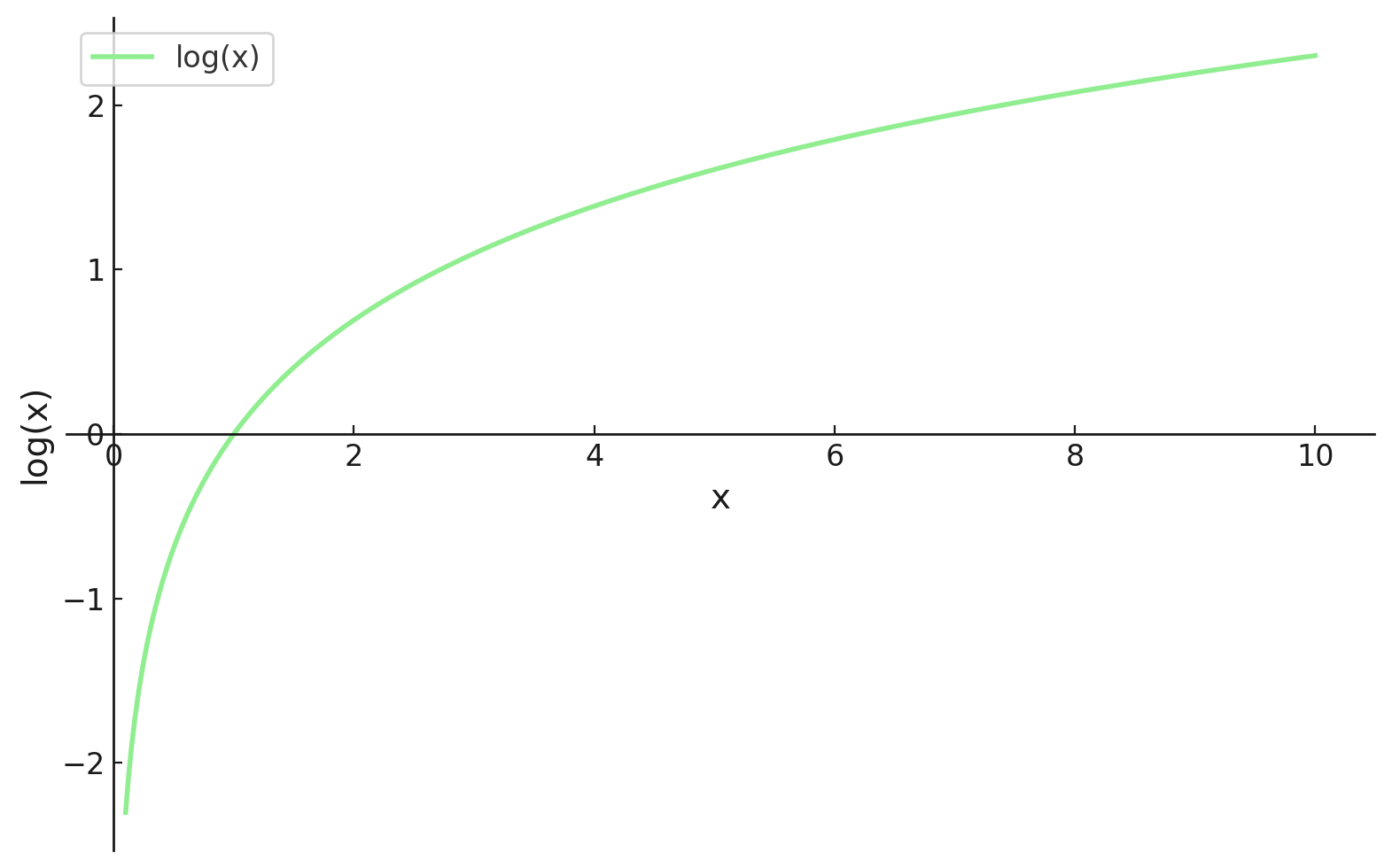
• O log transforma produtos em somas, que são muito mais fáceis de trabalhar, especialmente na hora de diferenciar.
• A função logarítmica é monotônica, então maximizar a log-verossimilhança dá o mesmo θ que maximizar a verossimilhança.

Passo 4: Encontrando o valor ideal

Agora estamos em um ponto em que podemos diferenciar, mas no machine learning, a gente geralmente quer minimizar nossas funções de perda. Felizmente, isso é bem fácil de resolver. 

Ao colocar um sinal de menos (ou seja, multiplicando por -1) no começo da nossa função, agora precisamos minimizar nossa função de perda, que agora é chamada de Função de Perda de Log-Verossimilhança Negativa.

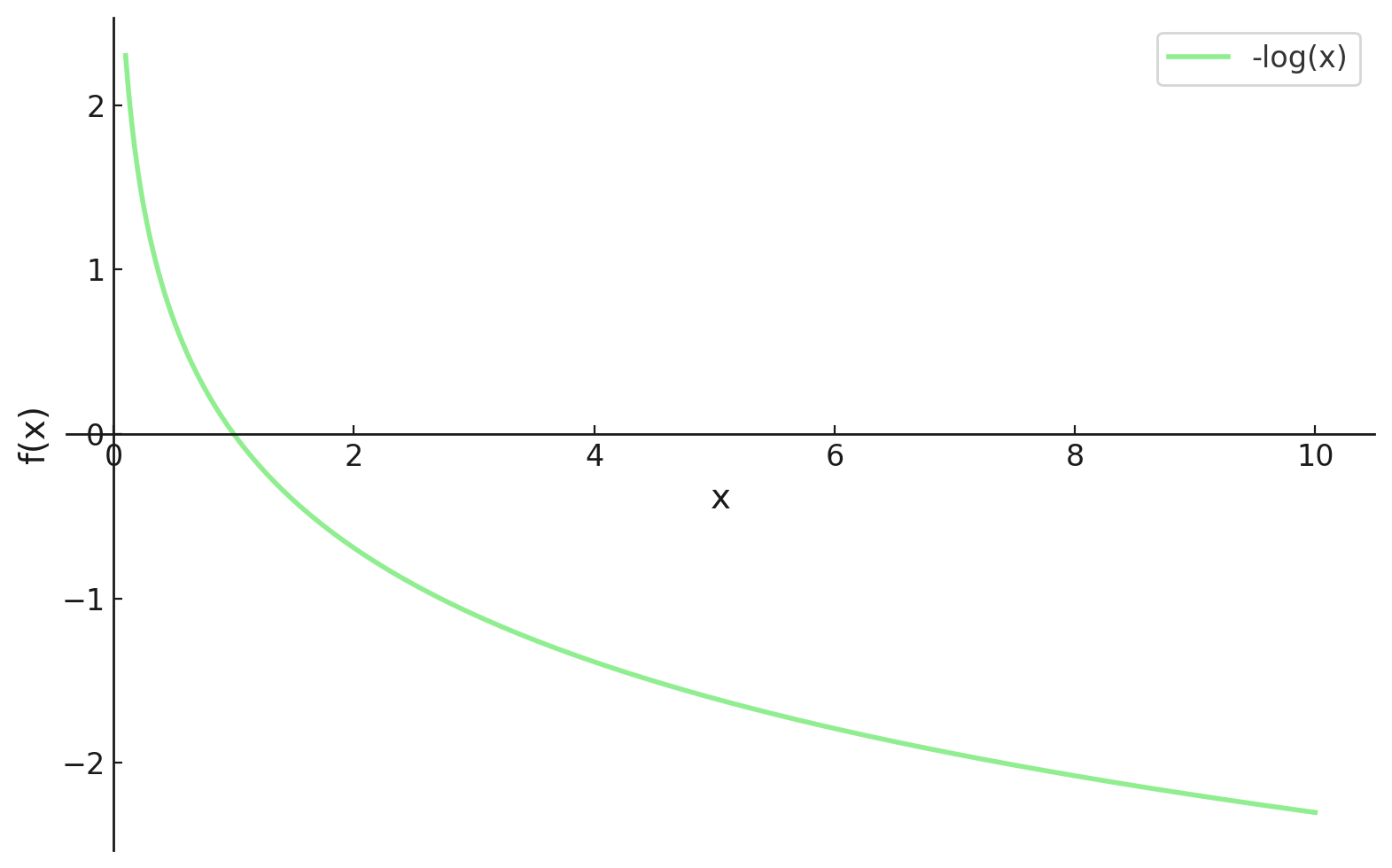
Agora, podemos usar cálculo para achar o valor de θ. Derivando a log-verossimilhança em relação a θ, colocando-a como zero e resolvendo para θ. Isso é porque o mínimo de uma função aparece onde a derivada é zero (e a segunda derivada é positiva).

Então, a equação final para MLE é:

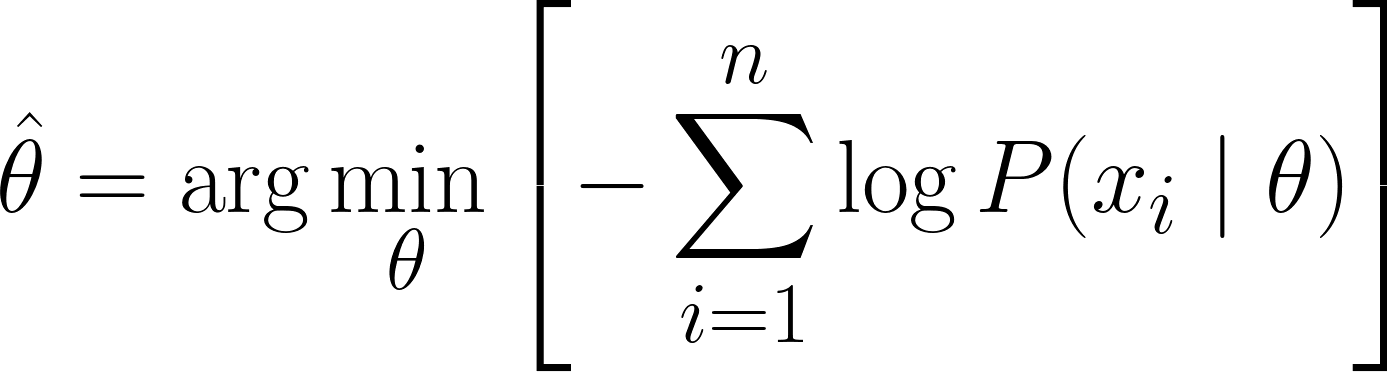
Exemplos práticos de MLE

Já que conseguimos chegar à equação MLE, vamos ver alguns exemplos práticos pra reforçar o que aprendemos.

Exemplo de jogadas de dados

Vamos começar com um exemplo simples e discreto: estimar a probabilidade de rolar um seis com um dado que pode estar viciado.

Imagina que a gente joga um dado 12 vezes e anota os resultados. Queremos modelar esses dados usando umadistribuição categórica de , mas vamos focar em estimar a probabilidade θ (theta) de rolar um seis. Neste exemplo:

• Parâmetro (θ): O valor que você quer estimar - Probabilidade de rolar um seis
• Data (x): Os resultados que vimos - 4 seis em 12 jogadas

Agora vamos calcular a função de verossimilhança, que, como conseguimos 4 seis em 12 jogadas, seria:

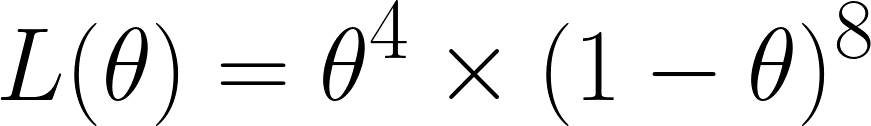
Chegamos a isso porque, das 12 vezes, obtivemos seis 4 vezes — então temos θ⁴ — e obtivemos outros números 8 vezes — então temos o termo (1 - θ)⁸. 

Lembre-se, temos multiplicado , já que assumimos que eles são condicionalmente independentes.

Agora, pegamos a log-verossimilhança negativa como discutimos anteriormente, o que nos dá esta equação:

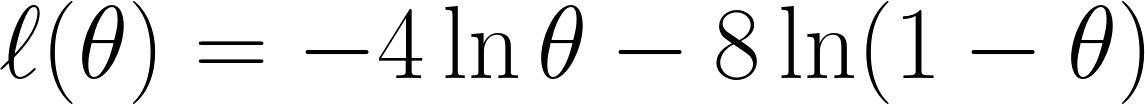
Por fim, diferenciamos a equação com em relação a θ e definimos como 0 (já que queremos encontrar o ponto mínimo):

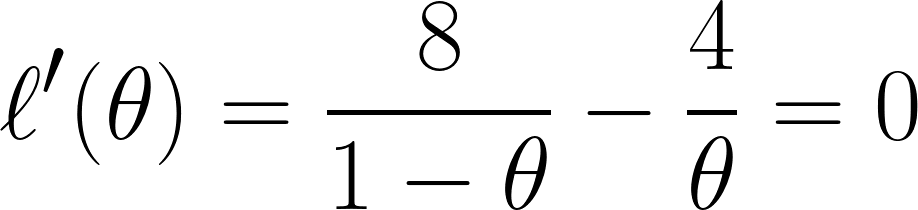
E com essa equação, dá pra concluir que θ é igual a ⅓. 

Observação: Se tivéssemos várias soluções para θ, também teríamos que achar a segunda derivada e ver quais valores de θ nos dariam um resultado positivo (para confirmar que encontramos um ponto mínimo). Isso pode ser confirmado através de uma função de exemplo na imagem abaixo:

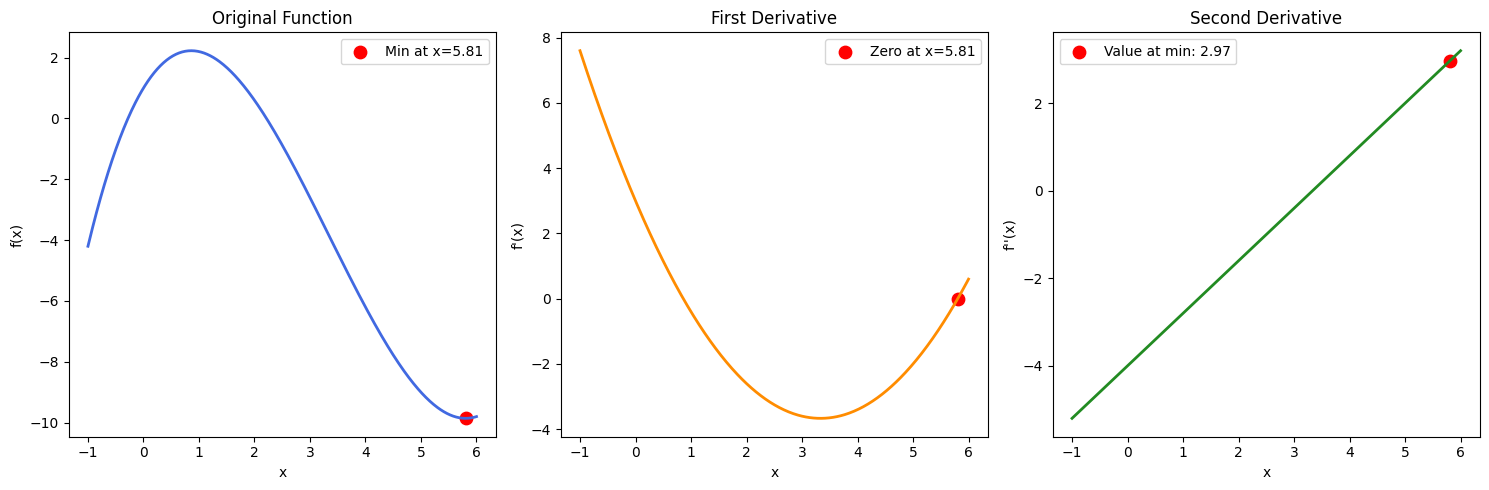
Exemplo de alturas

Agora vamos ver um exemplo contínuo: estimar a média de uma distribuição normal (gaussiana).

Vamos supor que temos um conjunto de dados com as alturas de 5 pessoas: 160, 165, 170, 175, 180 (em cm). Também vamos supor que eles são tirados de uma distribuição normal comuma média desconhecida μ (mu) e uma variância conhecida σ² (vamos dizer σ² = 25 pra facilitar).

• Parâmetro (μ): O valor que você quer estimar (a altura média)
• Data (x₁, x₂, ..., x₅): As alturas observadas

A função de probabilidade para a distribuição normal (com variância conhecida) é. 

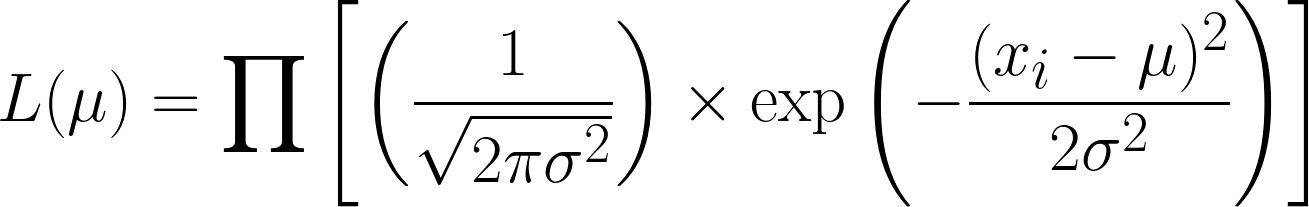
Isso é bem complicado, mas pegar o log negativo facilita as coisas. Espero que agora você consiga ver o poder de usar a função logarítmica na nossa equação. A equação que a gente consegue é essa:

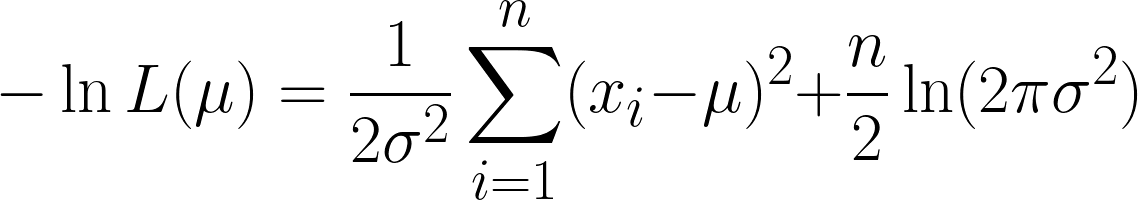
A gente consegue dois termos aqui, mas repara como o segundo termo pode ser ignorado quando a gente continua com a derivação, já que a gente está diferenciando em relação a μ, e o segundo termo não tem μ.

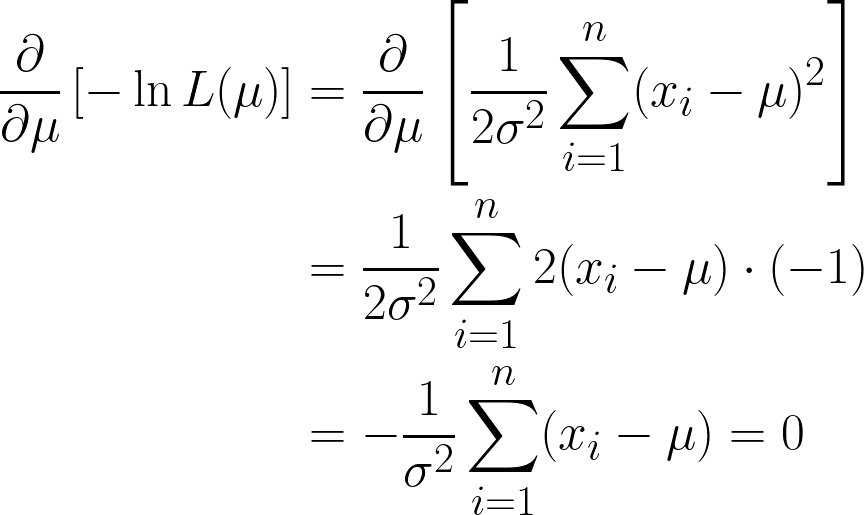
Estamos quase lá, mas dá uma olhada no μ entre parênteses. 

Como é uma coisa que tá sempre rolando, constante, podemos simplesmente multiplicá-lo por n, já que somar μ n vezes vai ser só n*μ.

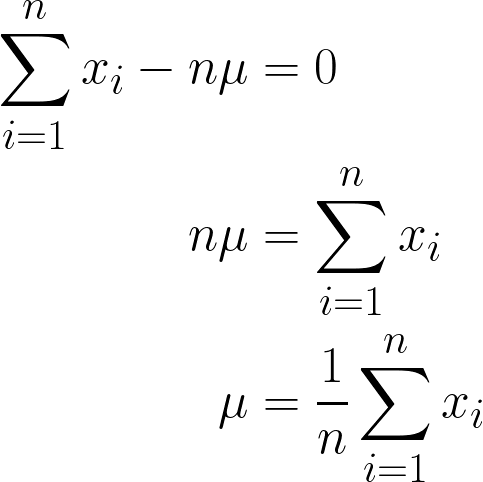
A resposta final que a gente chegou deve fazer sentido intuitivamente, já que é matematicamente expressa como a soma de todos os valores de x dividida por n (que é o número de observações que a gente tem), e isso também é o que significa definição de média!

Então, colocando os valores dos nossos dados nessa equação, dá pra calcular que a média é 170 cm. 

Para deixar isso mais visual, aqui está uma animação que mostra como a probabilidade muda conforme alteramos μ:

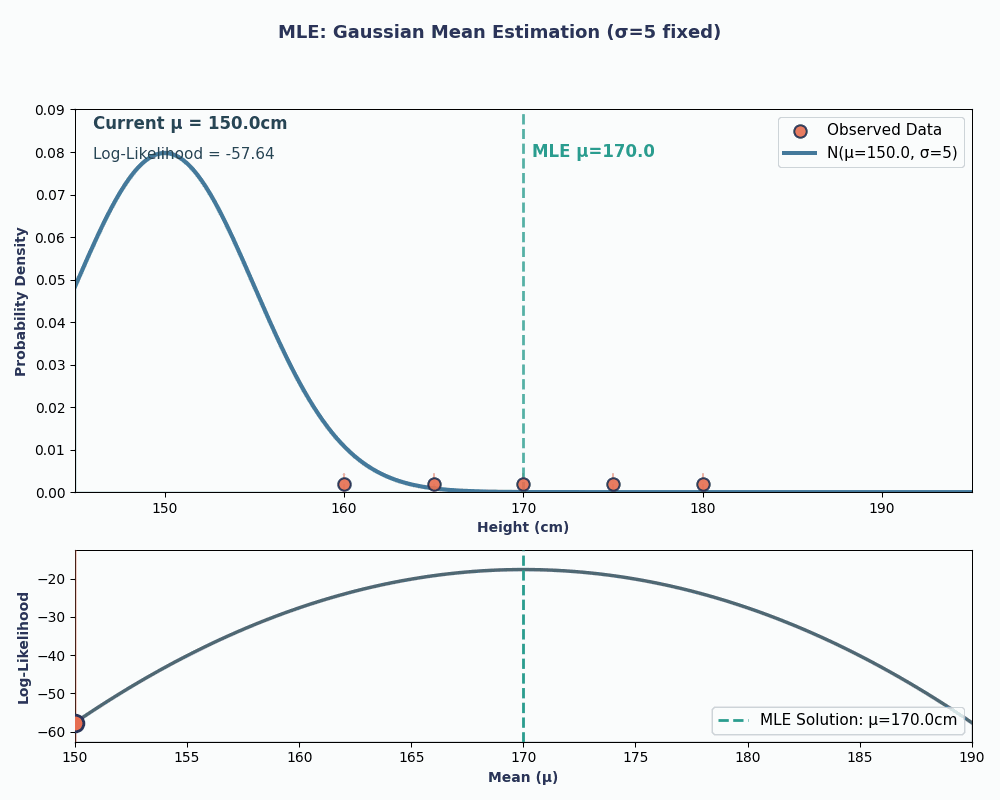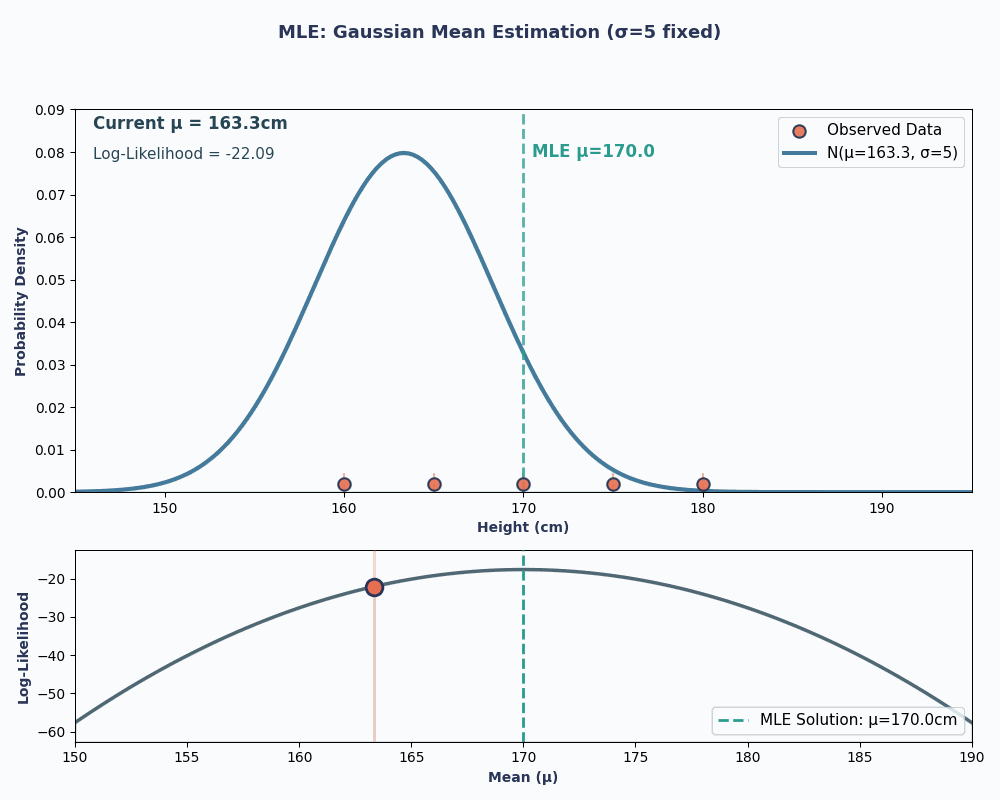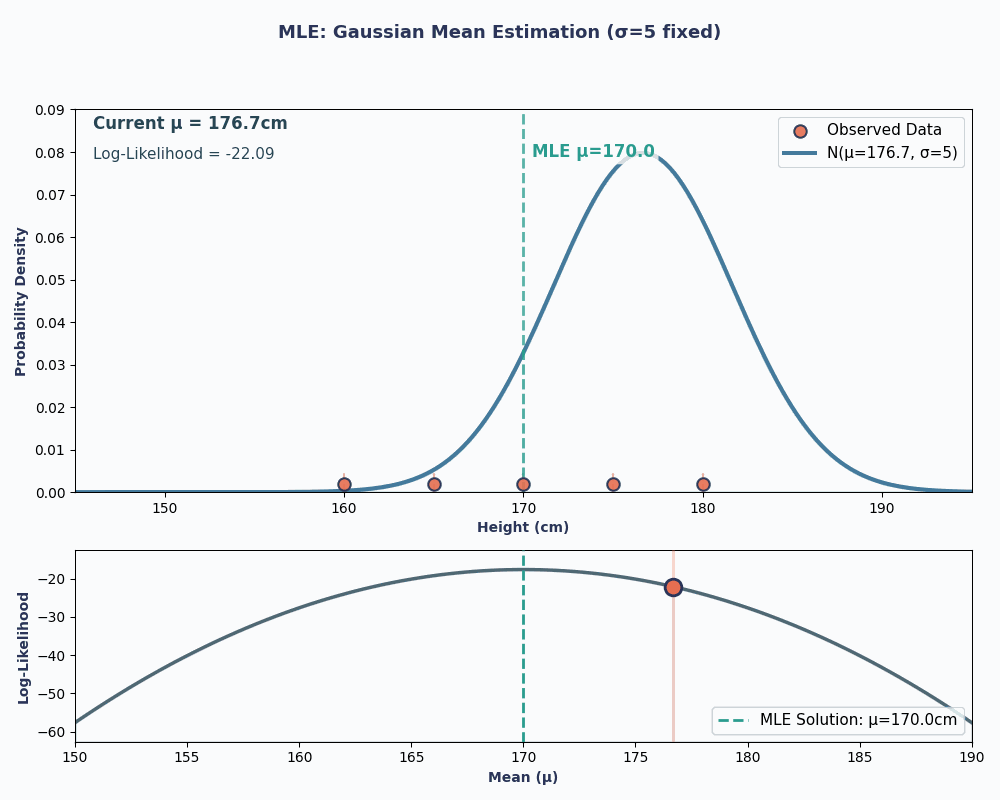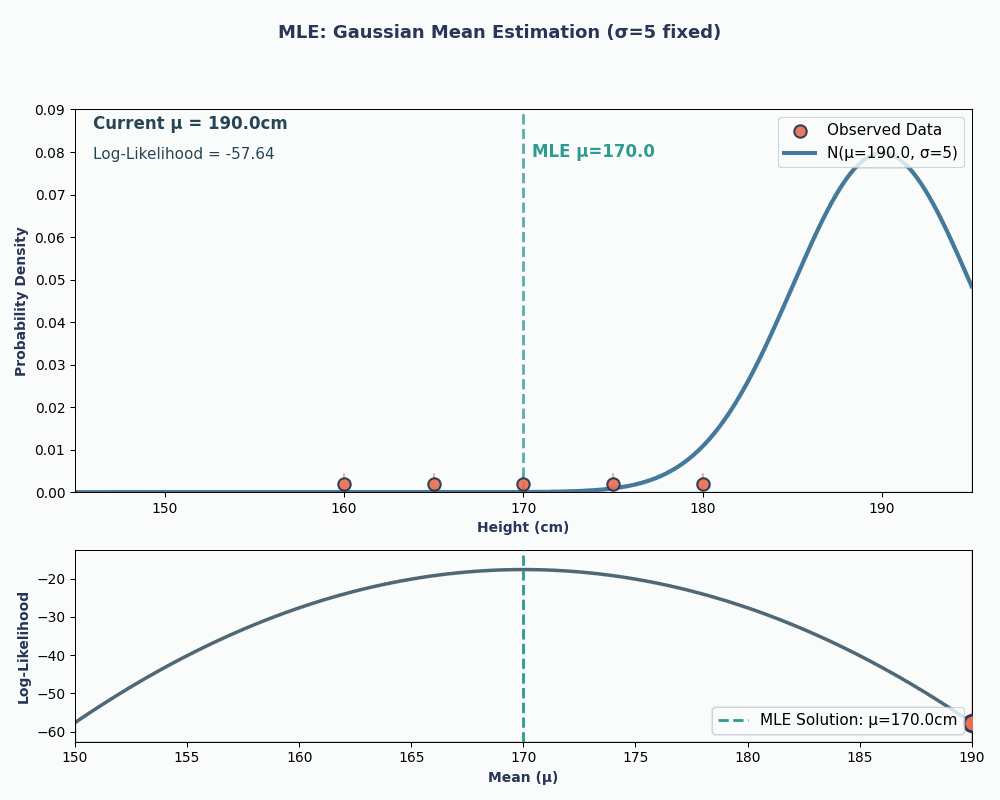
Nos dois exemplos, usar o MLE nos deu o valor do parâmetro que fez nossos dados observados parecerem mais prováveis no modelo escolhido. Claro, o MLEtambém pode funcionar comvários valores de parâmetros e , mas o cálculo vai demorar um pouco mais!

Codificação MLE

Agora que a gente já entendeu a estrutura por trás do MLE, vamos ver como codificar isso em Python. Vamos codificar a solução do exemplo anterior (alturas). 

# Importing libraries 
import numpy as np # used for handling arrays and mathematical operations.
from scipy.optimize import minimize # function that minimizes another function

# This is our sample data 
data = np.array([160, 165, 170, 175, 180])

# This was the variance we had assumed before
sigma_squared = 25

# Negative Log-Likelihood function
def negative_log_likelihood(mu):
    n = len(data) # Number of data points
    return 0.5 * n * np.log(2 * np.pi * sigma_squared) + \
           np.sum((data - mu)**2) / (2 * sigma_squared) # The NLL is for the Univariate Gaussian Distribution

# Optimizing the NLL
result = minimize(negative_log_likelihood, x0=170)  # initial guess

# Our final estimated mean
estimated_mu = result.x[0]
print(f"MLE estimate of mu: {estimated_mu}")

Estratégias computacionais e algoritmos

Repara que, quando estávamos codificando o exemplo anterior, criamos uma função negative_log_likelihood() que tinha a lógica principal para calcular o MLE de uma Distribuição Gaussiana Univariada.

Por um lado, dá pra dizer que a gente acabou codificando essa equação e usou o algoritmo de minimização de custo ( scipy.optimize ) pra minimizar essa função. Claro, essa ainda é uma solução totalmente viável, já que a Distribuição Gaussiana tem uma solução de forma fechada. 

Vamos ver outros jeitos de calcular soluções para MLE.

Soluções fechadas e quando elas funcionam

Como falamos acima, em alguns casos sortudos, dá pra resolver as equações MLE de forma analítica, o que significa que dá pra chegar a uma fórmula exata pra estimar os parâmetros. Elas são conhecidas comosoluções de forma fechada d , e geralmente são simples, intuitivas e rápidas de codificar e calcular.

Uma pergunta importante a se fazer agora é: quando é que existem soluções de forma fechada?

1. Quando a função de log-verossimilhança é diferenciável, côncava e algebricamente tratável.
2. Quando o modelo é simples o suficiente, geralmente com um ou dois parâmetros e variáveis ocultas.

Técnicas de otimização numérica

Para modelos mais complexos, não existem soluções analíticas ou elas são muito complicadas de se chegar. Nesses casos, usamosmétodos de otimização numérica de - algoritmos iterativos que procuram os parâmetros que maximizam a log-verossimilhança. Vamos explicar rapidinho:

1. Método de Newton-Raphson: Esse método usa os dois:

• A primeira derivada (gradiente) para determinar a inclinação, e
• A segunda derivada (Hessiana) para medir a curvatura e ajustar o tamanho do passo de acordo com ela.
• A regra de atualização é a seguinte:
• A principal vantagem é que ele tem convergência rápida perto do ideal.
• Mas, isso precisa calcular derivadas segundas, que podem ser meio complicadas. instáveis ou caras em dimensões elevadas.

2. Métodos quase Newton (por exemplo, BFGS):

• Aproxime a matriz Hessiana usando só derivadas de primeira ordem
• Usado em bibliotecas populares como scipy.optimize.minimize em Python (com BFGS como padrão).
• Mais estável numericamente e amplamente aplicável do que Newton-Raphson.

3. Algoritmo de maximização da expectativa (EM):

• Técnica de otimização especializada usada quando os dados envolvem variáveis latentes (ocultas)— valores que não observamos diretamente, mas que influenciam os dados.
• Esse algoritmo tem duas etapas:
• E-step (Expectativa): Calcule o valor esperado da log-verossimilhança usando as estimativas atuais dos parâmetros e os dados observados.
• Passo M (Maximização): Maximize essa log-verossimilhança esperada para atualizar as estimativas dos parâmetros.

Propriedades do MLE

A partir dos nossos exemplos e cálculos, fica claro que o MLE é útil. Formalmente falando, o MLE tem as seguintes propriedades: 

1. Consistência: À medida que o tamanho da amostra aumenta, o MLE converge para o valor real do parâmetro.
2. Normalidade assintótica: Para amostras grandes, a distribuição do MLE fica mais ou menos normal (em forma de sino) em torno do valor real do parâmetro. Essa é a base para construir intervalos de confiança.
3. Eficiência: Entre todos os estimadores imparciais, o MLE consegue a menor variância possível (chega ao limite inferior de Cramér-Rao, pelo menos assintoticamente).
4. Invariante: Se θ̂ é o MLE para θ, então, para qualquer função g, g(θ̂) é o MLE para g(θ). Em outras palavras, os MLEs são mantidos nas transformações.

Mas, tem casos em que usar MLE pode não ser a melhor ideia:

1. Amostras pequenas: A MLE pode ser tendenciosa quando a amostra é pequena. Por exemplo, o MLE para a variância (σ̂²) tende a subestimar a variância real (σ²).
2. Robustness: O MLE é sensível a valores atípicos e especificações incorretas do modelo. Alternativas como estimadores M podem dar estimativas mais robustas.
3. Alternativa bayesiana: A estimativa máxima a posteriori (MAP) junta informações prévias com a probabilidade, oferecendo uma visão bayesiana e, às vezes, estimativas mais estáveis, principalmente quando os dados são limitados.

Aplicações em modelagem estatística

Nesta seção, vamos ver onde o MLE é usado de verdade em Machine Learning e IA.

Regressão e classificação

Um dos lugares mais importantes onde o MLE aparece é na regressão logística. Aqui, estamos estimando a probabilidade de um resultado pertencer a uma determinada classe (como a perda de clientes) e fazemos isso ajustando parâmetros aum o para maximizar a probabilidade dos resultados observados.

Mesmo na regressão linear, se assumirmos erros normalmente distribuídos, a solução dos mínimos quadrados acaba sendo também o MLE.

Teste de hipóteses e escolha de modelos

A MLE também pode ser usada pra comparar modelos. 

Por exemplo, o teste da razão de verossimilhança (LRT) ajuda a ver se adicionar variáveis extras a um modelo melhora bastante o desempenho dele. Funciona comparando as probabilidades de dois modelos: um mais simples (nulo) e outro mais complexo (alternativo).

Também temos o Critério de Informação de Akaike (AIC), que penaliza a complexidade para evitar o sobreajuste. Essas ferramentas são muito usadas em áreas como finanças, medicina e marketing.

Limitações e alternativas ao MLE

Mesmo sendo super eficiente, tem suas desvantagens. Vamos dar uma olhada rápida nas dificuldades e no que podemos usar em vez disso.

Principais limitações do MLE

• Sensível a erros de especificação do modelo: Se o nosso modelo estiver errado (por exemplo, usando uma distribuição normal para dados assimétricos), o MLE vai nos dar resultados enganosos.
• Sensibilidade a valores atípicos: Alguns dados errados podem bagunçar completamente suas estimativas.
• Custo computacional: Para modelos grandes, principalmente com muitos parâmetros ou restrições, otimizar a probabilidade pode ser lento ou instável.
• Várias soluções: Às vezes, a superfície de probabilidade tem vários picos (máximos locais), o que dificulta encontrar a melhor solução.

Alternativas à estimativa de máxima verossimilhança

Quando o MLE não funciona bem, aqui estão algumas opções:

• MAP (Máximo a Posteriori): É como o MLE, mas tem uma crença prévia. Isso pode ajudar a estabilizar as estimativas quando os dados são limitados.
• Método dos Momentos: Combina momentos da amostra (como a média ou a variância) com os teóricos. É menos preciso que o MLE, mas muito fácil de calcular.
• Mínimos quadrados: Em casos como regressão linear com erros gaussianos, os mínimos quadrados e o MLE são a mesma coisa. Mas os mínimos quadrados ainda podem ser úteis quando o MLE é muito complicado.

Diferentes métodos funcionam melhor em diferentes situações. O MLE pode não ser sempre a resposta, mas geralmente é um ótimo ponto de partida.

Conclusão

A Estimativa de Máxima Verossimilhança é um dos métodos mais naturais e usados para estimar parâmetros. É a ideia de tornar os dados observadoso mais e es possível, e assim podem ser usados em muitos cenários diferentes, como lançamentos de moedas, alturas gaussianas, etc.

O MLE pode se adaptar a vários modelos e escalar com os dados, oferecendo elegância matemática e poder prático. Embora tenha suas desvantagens, especialmente em conjuntos de dados pequenos ou confusos, continua sendo uma ferramenta fundamental para aprender sobremachine learning e IA.

Se você está começando sua jornada no machine learning, não deixe de conferir nosso programa de carreira Cientista de Machine Learning em Python, que fala sobre aprendizado supervisionado, não supervisionado e profundo. 

Pronto pra entender melhor a Estimativa de Máxima Verossimilhança com exercícios práticos? Esses recursos podem te ajudar a colocar em prática o que você aprendeu e ganhar experiência:

• Maximizando a probabilidade, Parte 1 (Python): Calcule e visualize as log-verossimilhanças para ver claramente como as estimativas dos parâmetros são determinadas na prática.
• Regressão OLS: As ideias principais explicadas: Vamos ver a relação entre a regressão dos mínimos quadrados ordinários e o MLE quando a gente assume erros gaussianos, reforçando conceitos estatísticos básicos.
• Entendendo a regressão logística em Python: Descubra como a regressão logística usa o MLE para classificar e estimar parâmetros de forma eficaz.