Introducción a la estimación de máxima verosimilitud (MLE)

La estimación de parámetros es un paso fundamental en el análisis estadístico y el machine learning. Entre los diversos métodos disponibles,la estimación de máxima verosimilitud (MLE, por sus siglas en inglés) de la distribución de probabilidad ( ) es uno de los enfoques más utilizados debido a su naturaleza intuitiva, su rigor matemático y su amplia aplicabilidad a diferentes tipos de datos y modelos.

En este artículo, aprenderás qué es el MLE, explorarás sus fundamentos matemáticos a través de derivaciones detalladas y ejemplos, y descubrirás métodos computacionales prácticos para implementar el MLE de manera eficaz.

¿Qué es la estimación de máxima verosimilitud (MLE)?

La estimación de máxima verosimilitud (MLE) es un importante método estadístico que se utiliza para estimar los parámetros de una distribución de probabilidad mediante maximizar la función de verosimilitud.

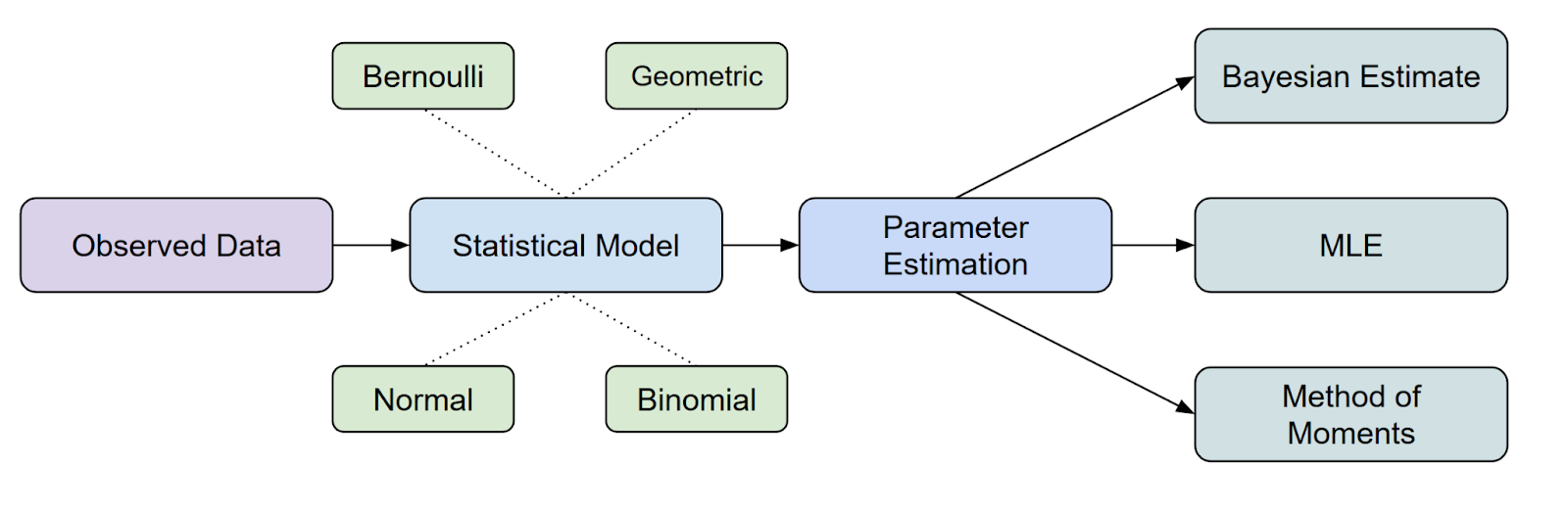
En cuanto al lugar que ocupa el MLE en la inferencia estadística, es uno de los métodos más comunes que tenemos para estimar parámetros.

Sin embargo, aquí es posible que surja otra pregunta. ¿Qué es una función de verosimilitud? Hablemos más sobre esto.

¿Qué es la función de verosimilitud?

Podemos pensar en la función de verosimilitud como una forma de medir en qué medida un conjunto concreto de parámetros explica los datos que has observado.

En otras palabras, responde a la pregunta: «Dados estos valores de los parámetros, ¿qué probabilidad hay de que veas estos datos?». Pero existe un error común entre probabilidad y verosimilitud:

• La probabilidad consiste en la predicción de datos a partir de parámetros.
• La medida de verosimilitud ( ) mide la plausibilidad de diferentes valores de parámetros, dados los datos observados. Es una función de parámetros para datos fijos. Por el contrario, la probabilidad es una función de los datos para parámetros fijos.

En resumen, la función de verosimilitud toma los parámetros de tu modelo como entrada y te da un número que representa la plausibilidad de esos parámetros, dados tus datos.

Cuanto mayor sea el valor de la función de verosimilitud, mejor explicarán tus datos esos parámetros.

Para decirlo de una forma aún más sencilla, la función de verosimilitud nos ayuda a «puntuara» diferentes opciones de parámetros, de modo que podamos elegir las que hacen que los datos observados sean más probables.

Ahora que hemos entendido la diferencia entre probabilidad y verosimilitud, así como para qué se utiliza el MLE, pasemos a la matemática subyacente.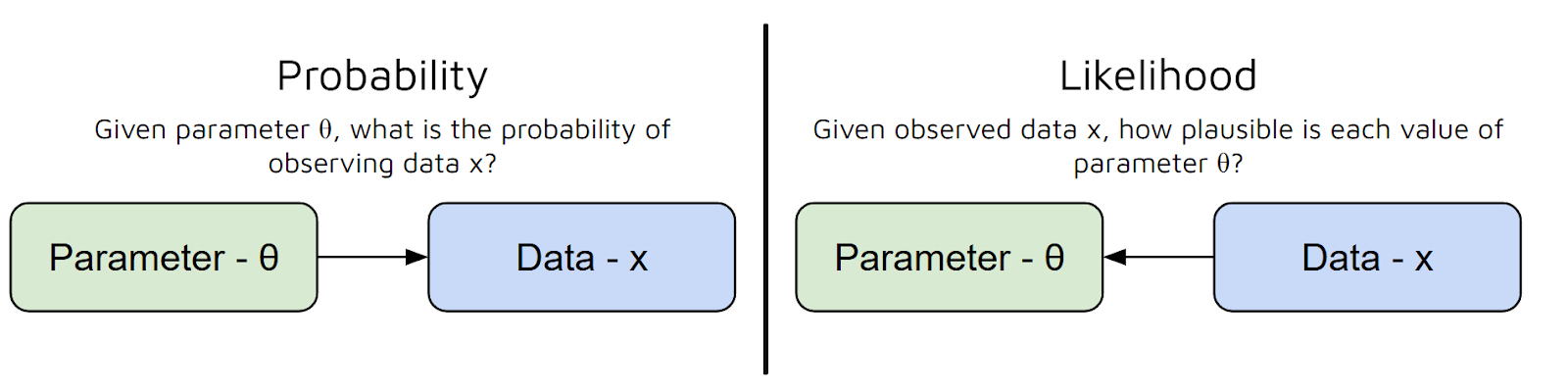

Cómo derivar la fórmula MLE

Antes de pasar a ejemplos concretos, veamos cómo se deriva el estimador de máxima verosimilitud (MLE) en general. Repasaremos cada paso y también explicaremos el razonamiento que hay detrás.

Paso 1: Definir modelo de probabilidad

Supongamos que tenemos un conjunto de datos: x₁, x₂, ..., xₙ. Creemos que estos puntos de datos se generan a partir de una distribución de probabilidad que depende de algún parámetro desconocido θ (theta). Nuestro objetivo principal es estimar θ. 

Por ejemplo, si tu conjunto de datos tratara sobre lanzamientos de monedas, θ podría ser la probabilidad de que salga cara. Si el conjunto de datos fuera continuo, como la estatura de los alumnos de la clase, θ podría ser la media de una distribución normal.

Paso 2: Escribir la función de verosimilitud

La función de verosimilitud mide la probabilidad de observar tus datos para diferentes valores de θ. Se define como:

Intuitivamente, nos preguntamos, dado que el parámetro θ toma un valor específico, ¿cuál es la probabilidad de observar este conjunto de datos en particular? 

Este conjunto de datos se representa como la probabilidad conjunta de observar los puntos de datos individuales (x₁, x₂, ..., xₙ), suponiendo que se generaron bajo el modelo parametrizado por θ.

Utilizando la regla de la cadena de la probabilidad, podemos expandir la ecuación anterior de la siguiente manera:

Sin embargo, ¡esta es una ecuación bastante complicada! Por lo tanto, partimos de la hipótesis de que los puntos de datos sonindependientes e es , más concretamente, independientes condicionalmente.

Al hacerlo, podemos obtener la probabilidad conjunta como el producto de las probabilidades individuales:

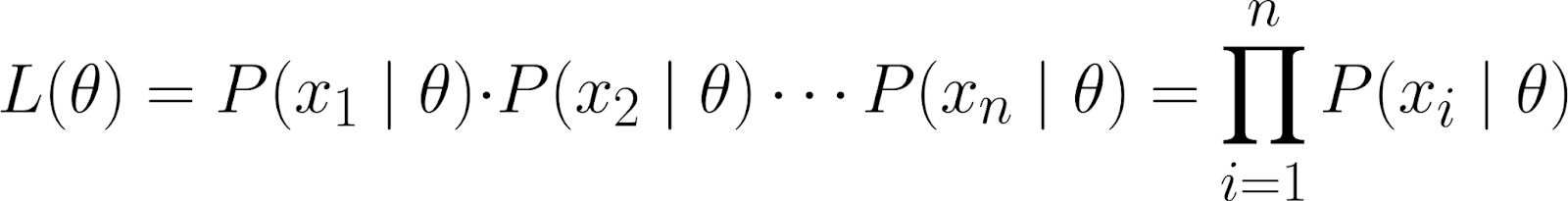
Dado que los puntos de datos observados son condicionalmente independientes de θ, sabemos que la siguiente ecuación es cierta:

Esto se debe a que hemos supuesto que, una vez conocido el valor de θ, los puntos de datos x₁ y x₂ son condicionalmente independientes.

Paso 3: Encuentra el valor de θ que maximiza la verosimilitud.

Nos encontramos en la situación de tener que encontrar los valores de θ que maximizan la función de verosimilitud(es decir, que hace que los datos observados sean más probables):

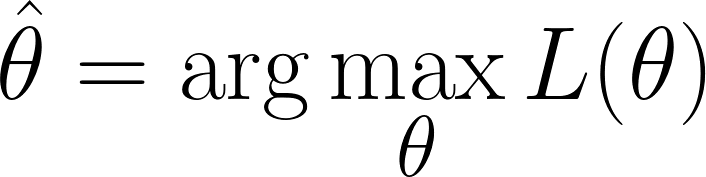
Sin embargo, recuerda que nuestra función de verosimilitud contiene un producto. Trabajar con productos puede ser complicado, especialmente cuando hay muchos puntos de datos. Para simplificar, tomamos ellogaritmo natural de la función de verosimilitud, ya que esto convierte el producto en una suma.

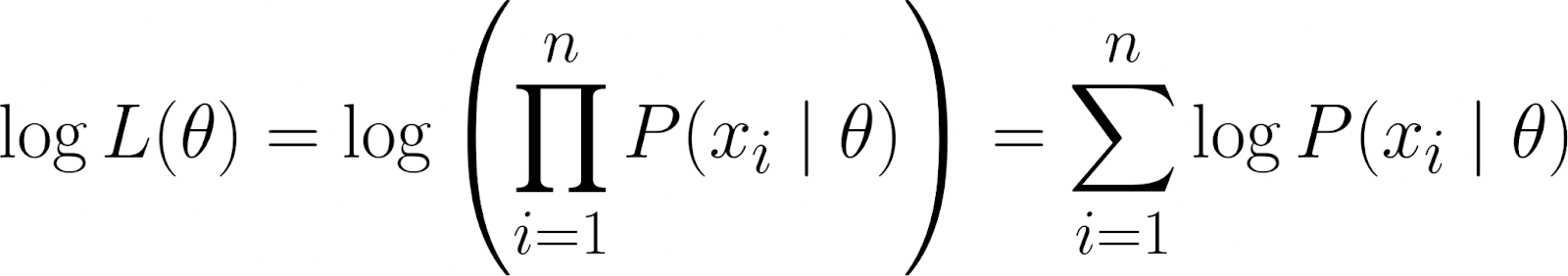
TEsto nos da la log-verosimilitud, que tiene algunas propiedades beneficiosas:

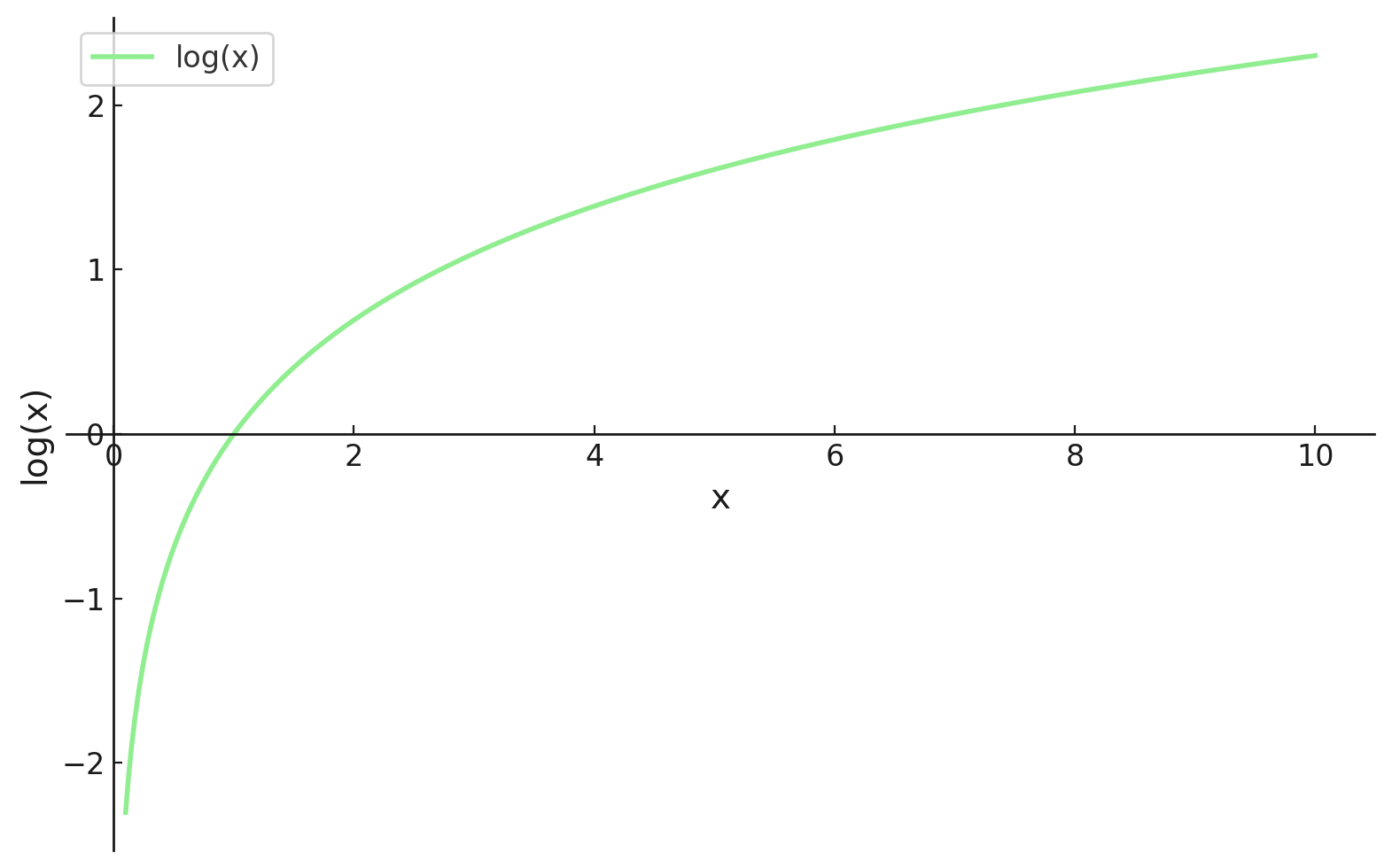
• El log convierte los productos en sumas, que son mucho más fáciles de manejar, especialmente a la hora de diferenciar.
• La función logarítmica es monotónica, por lo que maximizar la verosimilitud logarítmica da el mismo θ que maximizar la verosimilitud.

Paso 4: Encontrar el valor óptimo

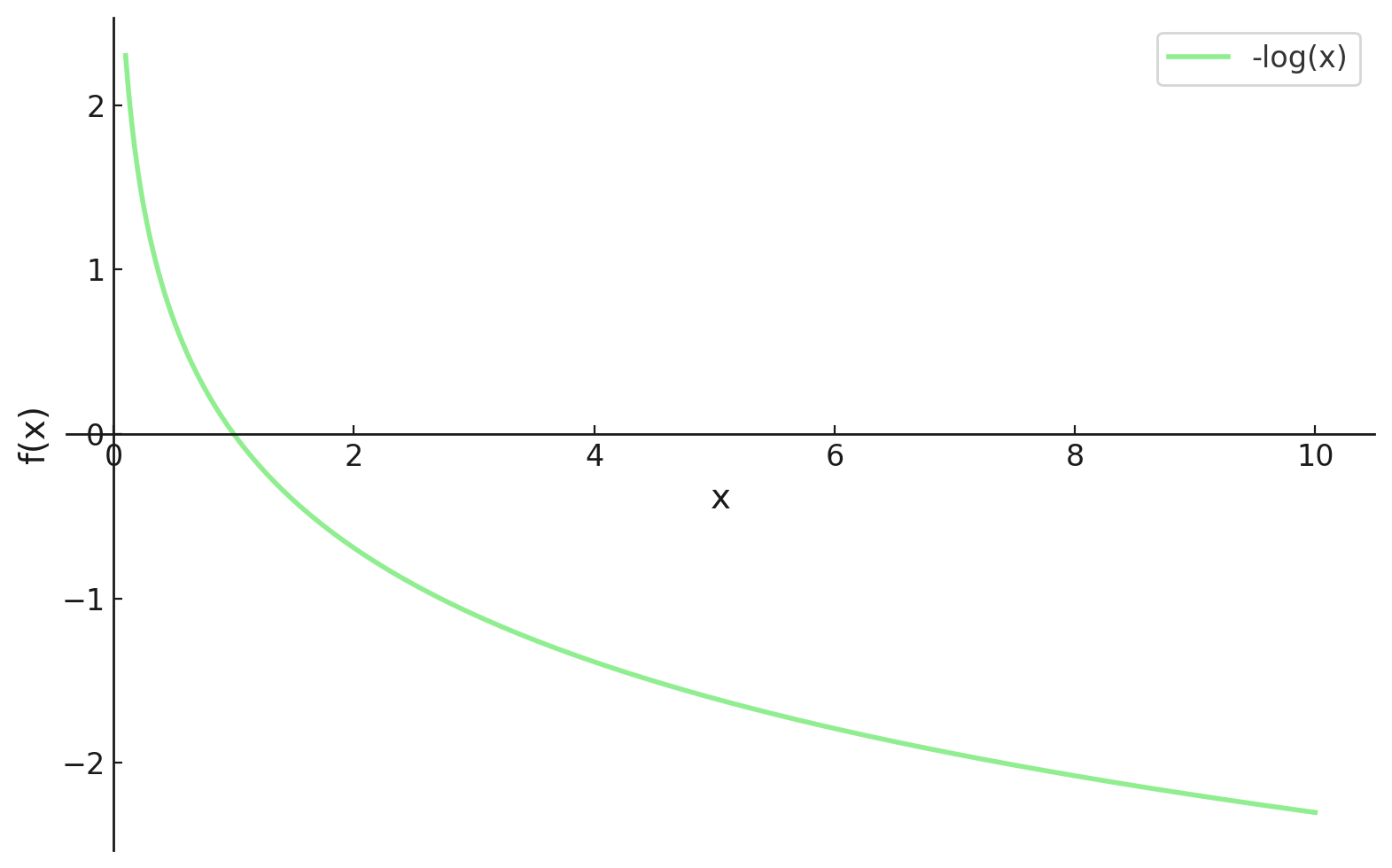
Ahora nos encontramos en un punto en el que podemos diferenciar, sin embargo, en el machine learning, tendemos a querer minimizar nuestras funciones de pérdida. Por suerte, esto tiene fácil solución. 

Al incluir un símbolo menos (es decir, multiplicar por -1) al principio de nuestra función, ahora tenemos que minimizar nuestra función de pérdida, que ahora se denomina función de pérdida de log-verosimilitud negativa.

Ahora, podemos usar el cálculo para obtener el valor de θ. Derivando la log-verosimilitud con respecto a θ, estableciéndola en cero y resolviendo para θ. Esto se debe a que el mínimo de una función se produce donde su derivada es cero (y la segunda derivada es positiva).

Por lo tanto, la ecuación final para MLE es:

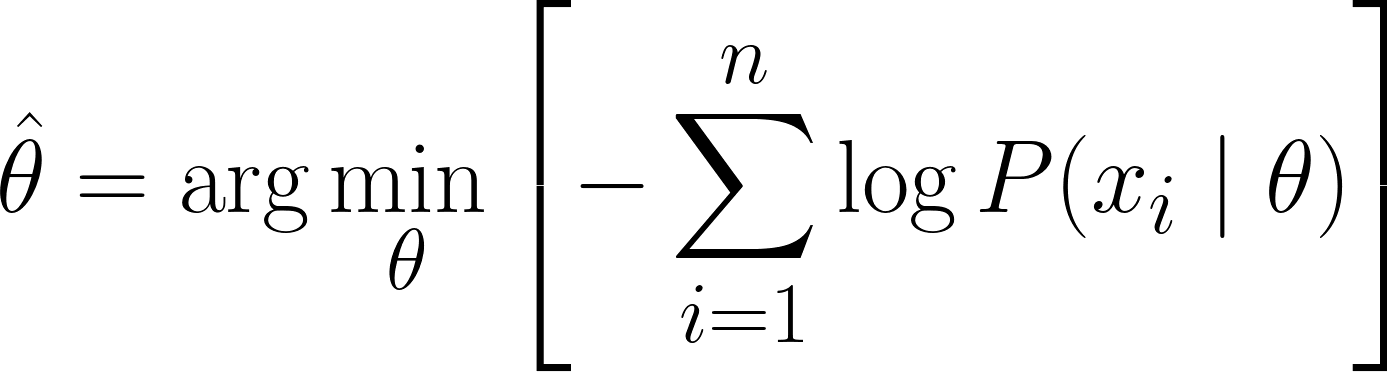
Ejemplos prácticos de MLE

Ahora que hemos derivado con éxito la ecuación MLE, veamos algunos ejemplos prácticos para consolidar nuestros conocimientos.

Ejemplo de tiradas de dados

Comencemos con un ejemplo sencillo y discreto: estimar la probabilidad de sacar un seis con un dado que puede estar sesgado.

Supongamos que lanzamos un dado 12 veces y anotamos los resultados. Queremos modelar estos datos utilizando unadistribución categórica e , pero centrémonos en estimar la probabilidad θ (theta) de sacar un seis. En este ejemplo:

• Parámetro (θ): El valor que deseas estimar: probabilidad de sacar un seis.
• Data (x): Los resultados que observamos: 4 seises en 12 tiradas.

Ahora calculamos la función de verosimilitud, que, dado que obtuvimos 4 seises en 12 tiradas, sería:

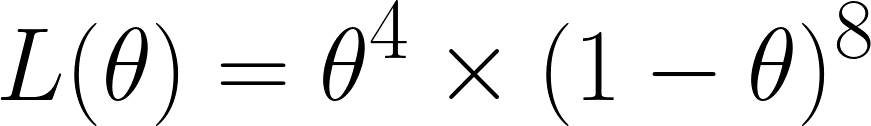
Hemos obtenido este resultado porque, de las 12 veces, hemos obtenido un seis 4 veces, por lo que tenemos θ⁴, y hemos obtenido otros resultados distintos del seis 8 veces, por lo que tenemos el término (1 - θ)⁸. 

Recordemos que tenemos multiplicado , ya que hemos supuesto que son condicionalmente independientes.

Ahora tomamos la log-verosimilitud negativa tal y como hemos comentado anteriormente, lo que nos da esta ecuación:

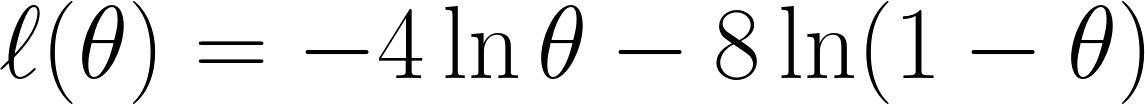
Por último, diferenciamos la ecuación con respecto a θ y la establecemos en 0 (ya que queremos encontrar el punto mínimo):

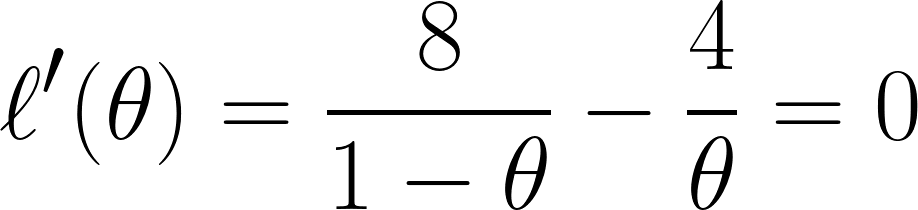
Y a través de esta ecuación, podemos concluir que θ es igual a ⅓ . 

Nota: Si hubiéramos obtenido múltiples soluciones de θ, entonces también tendríamos que hallar la segunda derivada y ver qué valores de θ nos darían un resultado positivo (para confirmar que hemos encontrado un punto mínimo). Esto se puede confirmar mediante una función de ejemplo en la imagen siguiente:

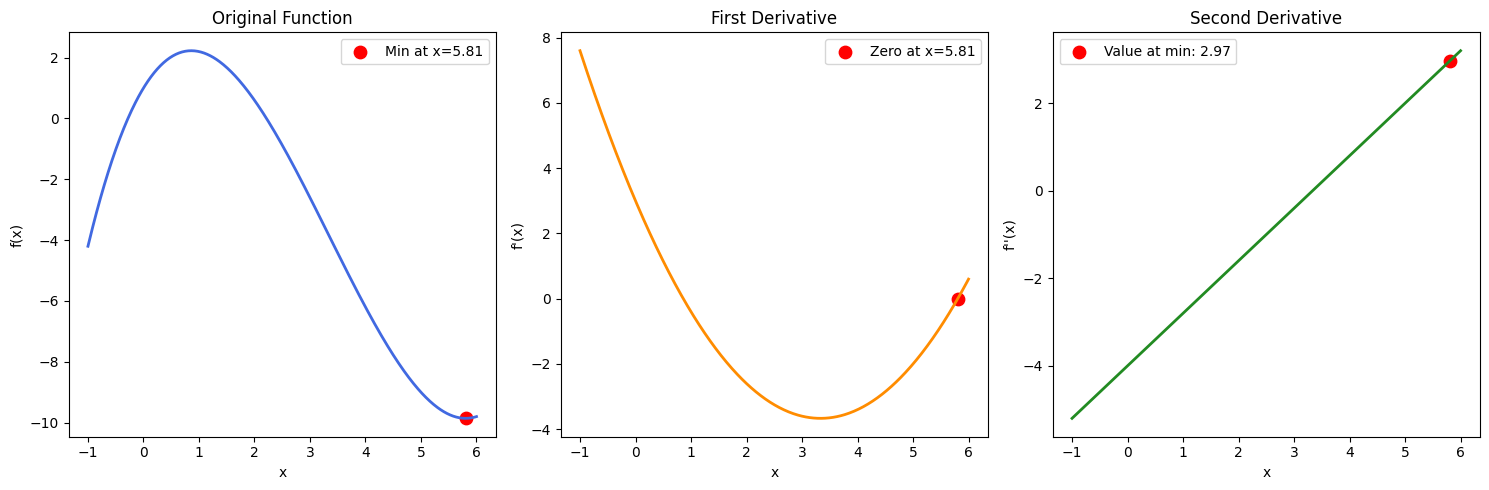
Ejemplo de alturas

Veamos ahora un ejemplo continuo: estimar la media de una distribución normal (gaussiana).

Supongamos que tenemos un conjunto de datos con las alturas de 5 personas: 160, 165, 170, 175, 180 (en cm). También asumiremos que se han extraído de una distribución normal conuna media desconocida μ (mu) y una varianz e conocida σ² (supongamos que σ² = 25 para simplificar).

• Parámetro (μ): El valor que deseas estimar (la altura media)
• Datos (x₁, x₂, ..., x₅): Las alturas observadas

La función de verosimilitud para la distribución normal (con varianza conocida) es. 

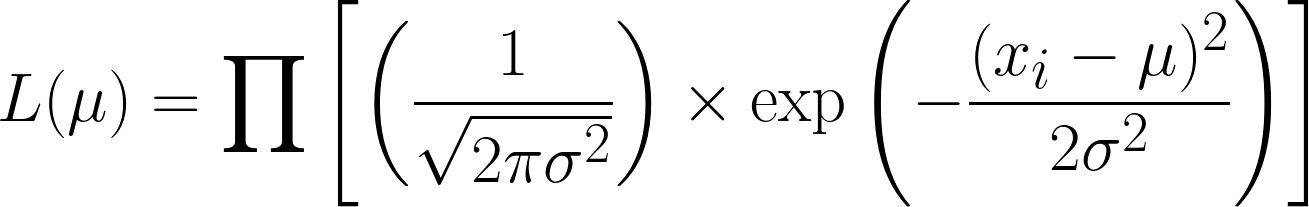
Esto es muy complicado, pero tomar el logaritmo negativo facilita las cosas. Esperamos que ahora puedas ver el poder de usar la función logarítmica en nuestra ecuación. La ecuación que obtenemos es la siguiente:

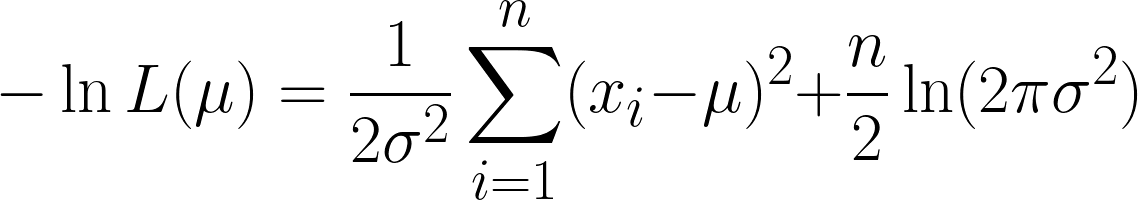
Aquí obtenemos dos términos, pero fíjate en que el segundo término puede ignorarse cuando procedemos a la diferenciación, ya que estamos diferenciando con respecto a μ, y el segundo término no contiene μ.

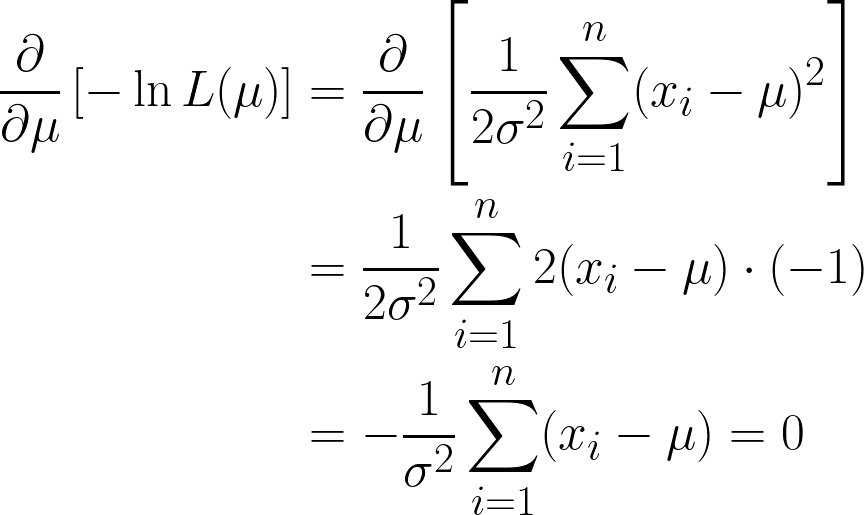
Ya casi estamos, pero fíjate en μ entre paréntesis. 

Dado que se trata de un constante, podemos simplemente multiplicarlo por n, ya que sumar μ n veces será simplemente n*μ.

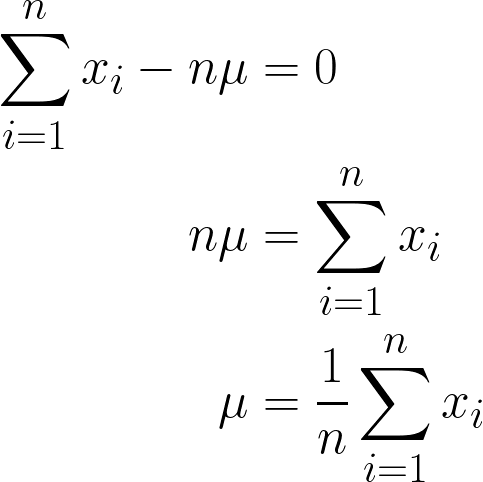
La respuesta final que hemos obtenido debería tener sentido intuitivo, ya que se expresa matemáticamente como la suma de todos los valores de x dividida por n (que es el número de observaciones que tenemos), y esta es también la definición de la media.

Por lo tanto, al introducir los valores de nuestros datos en esta ecuación, obtenemos que la media es de 170 cm. 

Para que esto sea más visual, aquí tienes una animación que muestra cómo cambia la probabilidad a medida que cambiamos μ:

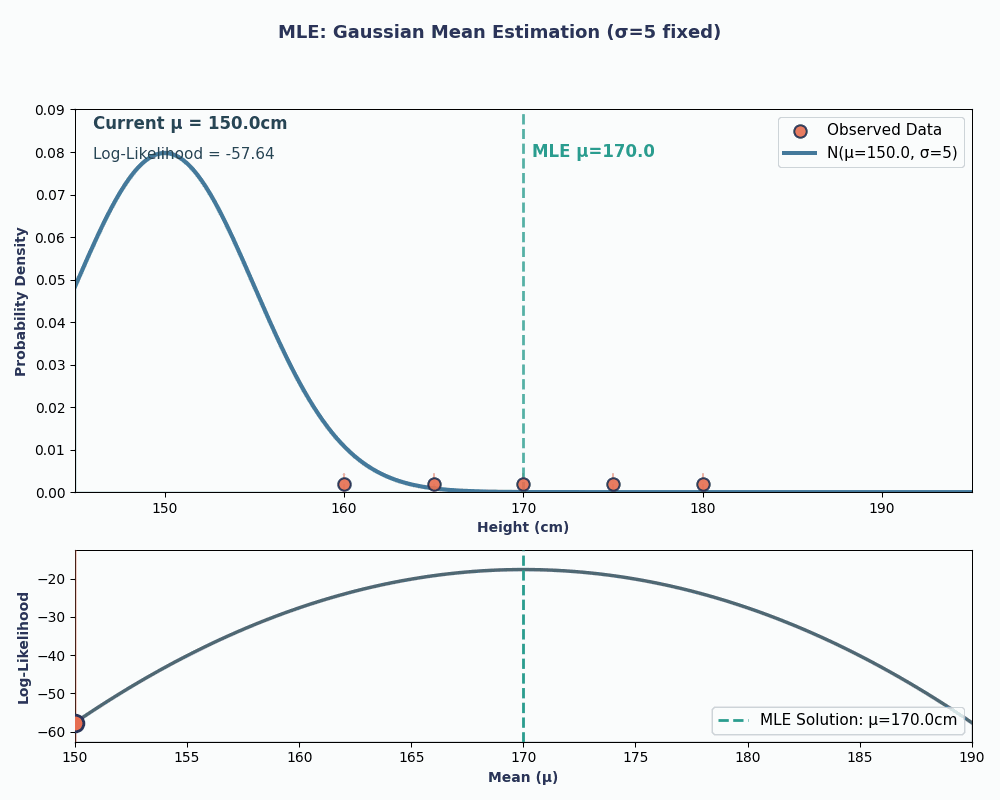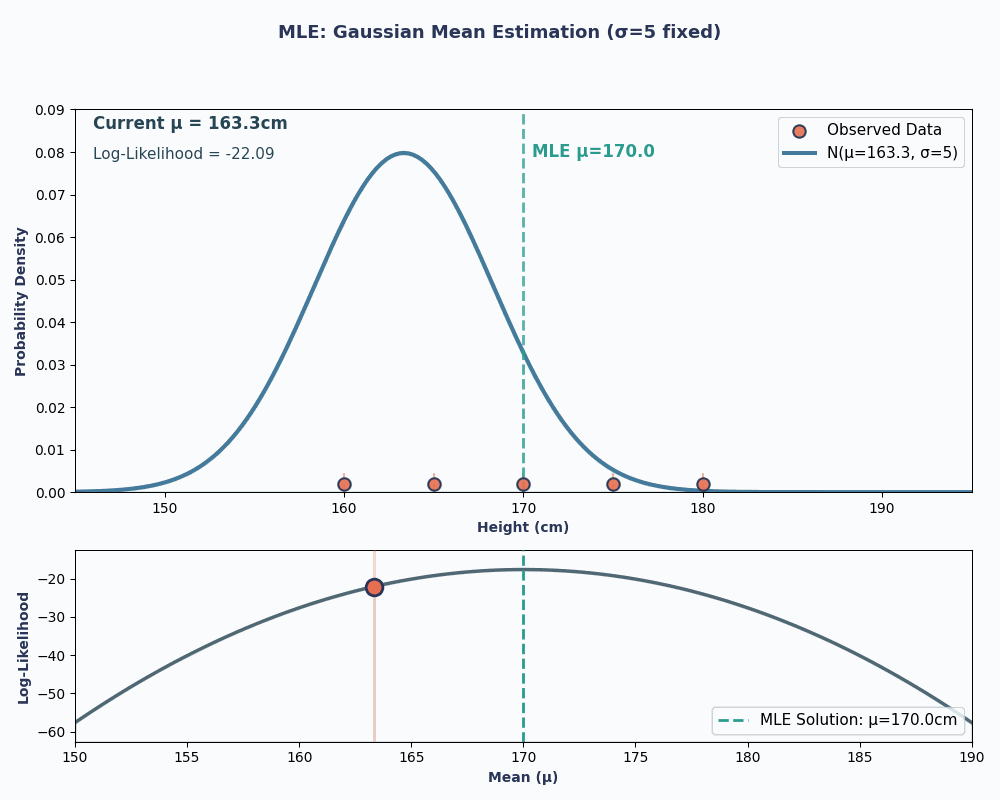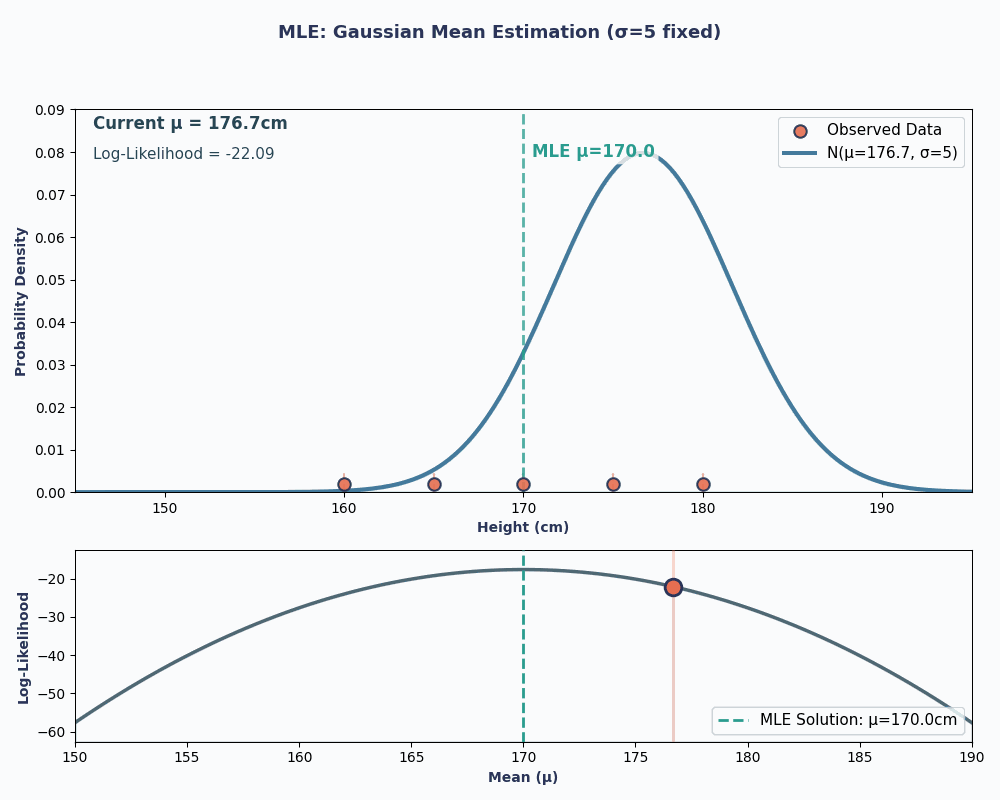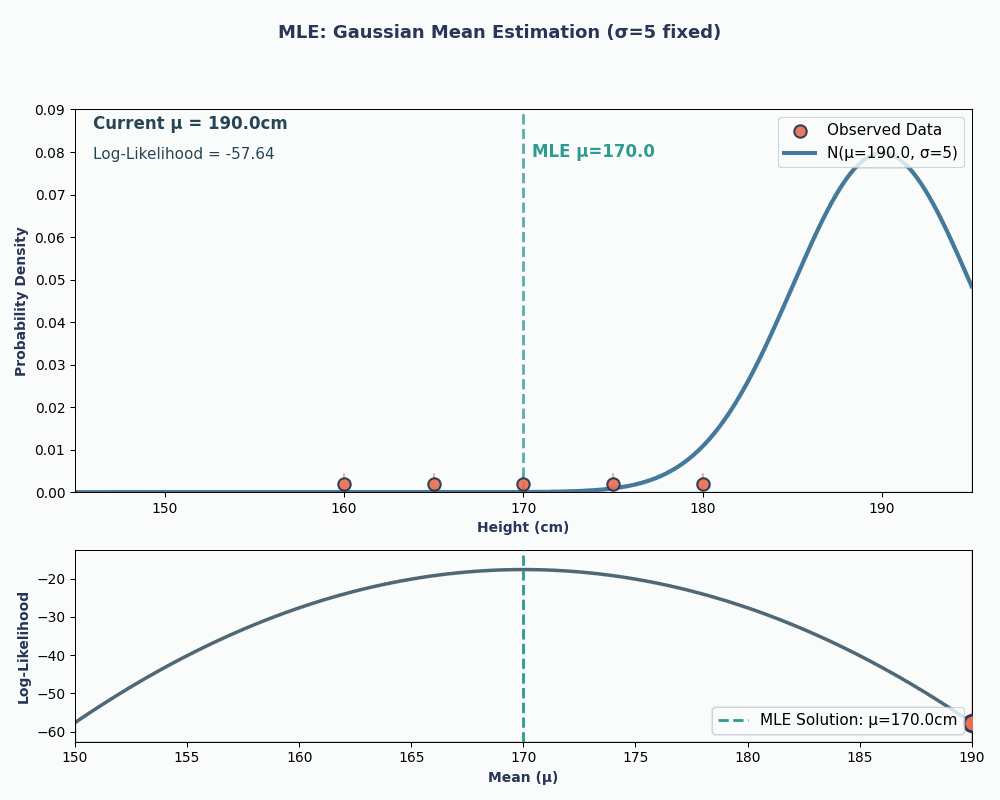
En ambos ejemplos, el uso del MLE nos proporcionó el valor del parámetro que hacía que los datos observados fueran más probables según el modelo elegido. Obviamente, MLEtambién puede funcionar convalores de parámetros múltiples e es , aunque el cálculo sería un poco más largo.

Codificación MLE

Ahora que hemos entendido la estructura subyacente de MLE, veamos cómo codificarlo en Python. Vamos a codificar la solución del ejemplo anterior (alturas). 

# Importing libraries 
import numpy as np # used for handling arrays and mathematical operations.
from scipy.optimize import minimize # function that minimizes another function

# This is our sample data 
data = np.array([160, 165, 170, 175, 180])

# This was the variance we had assumed before
sigma_squared = 25

# Negative Log-Likelihood function
def negative_log_likelihood(mu):
    n = len(data) # Number of data points
    return 0.5 * n * np.log(2 * np.pi * sigma_squared) + \
           np.sum((data - mu)**2) / (2 * sigma_squared) # The NLL is for the Univariate Gaussian Distribution

# Optimizing the NLL
result = minimize(negative_log_likelihood, x0=170)  # initial guess

# Our final estimated mean
estimated_mu = result.x[0]
print(f"MLE estimate of mu: {estimated_mu}")

Estrategias computacionales y algoritmos

Observa que, al codificar el ejemplo anterior, creamos una función negative_log_likelihood() que contenía la lógica principal para calcular el MLE de una distribución gaussiana univariante.

Por un lado, se podría argumentar que, en última instancia, codificamos esta ecuación de forma rígida y utilizamos el algoritmo de búsqueda por ensayo y error ( scipy.optimize ) para minimizar esa función. Por supuesto, esta sigue siendo una solución totalmente viable, ya que la distribución gaussiana tiene una solución de forma cerrada. 

Exploremos otros métodos para calcular soluciones para MLE.

Soluciones cerradas y cuándo se aplican

Como hemos comentado anteriormente, en algunos casos afortunados, podemos resolver las ecuaciones MLE de forma analítica, lo que significa que podemos derivar una fórmula exacta para las estimaciones de los parámetros. Se conocen comosoluciones de forma cerrada de , y suelen ser sencillas, intuitivas y rápidas de codificar y calcular.

Una pregunta importante que hay que plantearse ahora es: ¿cuándo existen soluciones de forma cerrada?

1. Cuando la función de verosimilitud logarítmica es diferenciable, cóncava y algebraicamente manejable.
2. Cuando el modelo es lo suficientemente simple, que suele incluir uno o dos parámetros y no variables ocultas.

Técnicas de optimización numérica

Para modelos más complejos, no existen soluciones analíticas o son demasiado complicadas de obtener. En estos casos, utilizamosmétodos de optimización numérica , algoritmos iterativos que buscan los parámetros que maximizan la log-verosimilitud. Vamos a explicarlos brevemente:

1. Método de Newton-Raphson: Este método utiliza ambos:

• La primera derivada (gradiente) para determinar la pendiente, y
• La segunda derivada (Hessiana) para medir la curvatura y ajustar el tamaño del paso en consecuencia.
• La regla de actualización es la siguiente:
• Su principal ventaja es que tiene rápida convergencia cerca del óptimo.
• Sin embargo, requiere calcular derivadas segundas, que pueden ser inestables o costosas en dimensiones elevadas.

2. Métodos cuasi-Newton (por ejemplo, BFGS):

• Aproximar la matriz Hessiana utilizando únicamente derivadas de primer orden.
• Se utiliza en bibliotecas populares como scipy.optimize.minimize en Python (con BFGS como valor predeterminado).
• Más estable numéricamente y ampliamente aplicable que Newton-Raphson.

3. Algoritmo de maximización de la expectativa (EM):

• Técnica de optimización especializada que se utiliza cuando los datos incluyen variables latentes (ocultas), es decir, valores que no observamos directamente pero que influyen en los datos.
• Este algoritmo consta de dos pasos:
• E-step (Expectativa): Calcula el valor esperado de la log-verosimilitud utilizando las estimaciones actuales de los parámetros y los datos observados.
• Paso M (maximización): Maximiza esta verosimilitud logarítmica esperada para actualizar las estimaciones de los parámetros.

Propiedades del MLE

A partir de nuestros ejemplos y cálculos, queda claro que el MLE es útil. Hablando formalmente, el MLE tiene las siguientes propiedades: 

1. Coherencia: A medida que aumenta el tamaño de la muestra, el MLE converge hacia el valor real del parámetro.
2. Normalidad asintótica: Para muestras grandes, la distribución del MLE se vuelve aproximadamente normal (en forma de campana) alrededor del valor real del parámetro. Esta es la base para construir intervalos de confianza.
3. Eficiencia: Entre todos los estimadores imparciales, el MLE alcanza la varianza más baja posible (alcanza el límite inferior de Cramér-Rao, al menos asintóticamente).
4. Invarianza: Si θ̂ es el MLE para θ, entonces para cualquier función g, g(θ̂) es el MLE para g(θ). En otras palabras, los MLE se conservan bajo transformaciones.

Sin embargo, hay situaciones en las que el uso de MLE podría no ser la mejor opción:

1. Muestras pequeñas: El MLE puede estar sesgado cuando el tamaño de la muestra es pequeño. Por ejemplo, el MLE para la varianza (σ̂²) tiende a subestimar la varianza real (σ²).
2. Robustez: El MLE es sensible a los valores atípicos y a las especificaciones erróneas del modelo. Alternativas como los estimadores M pueden proporcionar estimaciones más sólidas.
3. Alternativa bayesiana: La estimación máxima a posteriori (MAP) combina la información previa con la probabilidad, ofreciendo una perspectiva bayesiana y, en ocasiones, estimaciones más estables, especialmente con datos limitados.

Aplicaciones en el modelado estadístico

En esta sección, exploraremos dónde se utiliza realmente el MLE en el machine learning y la IA.

Regresión y clasificación

Uno de los ámbitos más importantes en los que aparece el MLE es la regresión logística. Aquí, estamos estimando la probabilidad de que un resultado pertenezca a una clase determinada (como la pérdida de clientes) y lo hacemos ajustando los parámetros aun o para maximizar la probabilidad de los resultados observados.

Incluso en regresiones lineales, si asumimos que los errores se distribuyen normalmente, la solución de mínimos cuadrados resulta ser también el MLE.

Prueba de hipótesis y selección de modelos

El MLE también se puede utilizar para comparar modelos. 

Por ejemplo, la prueba de razón de verosimilitud (LRT, por sus siglas en inglés) nos ayuda a comprobar si añadir variables adicionales a un modelo mejora significativamente su rendimiento. Funciona comparando las probabilidades de dos modelos: uno más simple (nulo) y otro más complejo (alternativo).

También tenemos el criterio de información de Akaike (AIC), que penaliza la complejidad para evitar el sobreajuste. Estas herramientas se utilizan ampliamente en campos como las finanzas, la medicina y el marketing.

Limitaciones y alternativas al MLE

Aunque es potente, tiene sus inconvenientes. Repasemos rápidamente cuáles son sus puntos débiles y qué podemos utilizar en su lugar.

Limitaciones clave del MLE

• Sensible a la especificación errónea del modelo: Si nuestro modelo es incorrecto (por ejemplo, si utilizas una distribución normal para datos sesgados), el MLE nos dará resultados engañosos.
• Sensibilidad a valores atípicos: Unos pocos datos erróneos pueden desvirtuar por completo tus estimaciones.
• Coste computacional: En modelos grandes, especialmente con muchos parámetros o restricciones, la optimización de la verosimilitud puede ser lenta o inestable.
• Múltiples soluciones: A veces, la superficie de probabilidad tiene varios picos (máximos locales), lo que dificulta encontrar la mejor solución.

Alternativas a la estimación de máxima verosimilitud

Cuando MLE no funciona bien, aquí tienes algunas opciones:

• MAP (máximo a posteriori): Igual que MLE, pero añade una creencia previa. Esto puede ayudar a estabilizar las estimaciones cuando los datos son limitados.
• Método de los momentos: Compara momentos muestrales (como la media o la varianza) con los teóricos. Es menos preciso que el MLE, pero muy fácil de calcular.
• Mínimos cuadrados: En casos como la regresión lineal con errores gaussianos, los mínimos cuadrados y el MLE son lo mismo. Pero los mínimos cuadrados pueden seguir siendo útiles cuando el MLE es demasiado complejo.

Diferentes métodos funcionan mejor en diferentes situaciones. El MLE puede que no siempre sea la respuesta, pero a menudo es un excelente punto de partida.

Conclusión

La estimación de máxima verosimilitud es uno de los métodos más naturales y ampliamente utilizados para la estimación de parámetros. Se trata de hacer que los datos observadossean lo má es posible, de modo que puedan utilizarse en muchos escenarios diferentes, como lanzamientos de monedas, alturas gaussianas, etc.

El MLE se puede adaptar a distintos modelos y escalar con datos, lo que ofrece elegancia matemática y potencia práctica. Aunque tiene sus propios inconvenientes, especialmente en conjuntos de datos pequeños o desordenados, sigue siendo una herramienta fundamental para aprendersobre machine learning (aprendizaje automático) y la inteligencia artificial (IA).

Si estás iniciando tu andadura en el machine learning, no te pierdas nuestro programa de desarrollo profesional Machine Learning Scientist in Python, que explora el aprendizaje supervisado, no supervisado y profundo. 

¿Estás listo para profundizar tus conocimientos sobre la estimación de máxima verosimilitud con ejercicios prácticos? Estos recursos pueden ayudarte a aplicar tus conocimientos y adquirir experiencia práctica:

• Maximizar la probabilidad, parte 1 (Python): Calcula y visualiza las verosimilitudes logarítmicas para ver claramente cómo se determinan las estimaciones de los parámetros en la práctica.
• Regresión OLS: Las ideas clave explicadas: Explora la conexión entre la regresión por mínimos cuadrados ordinarios y el MLE cuando se asumen errores gaussianos, reforzando los conceptos estadísticos básicos.
• Comprender la regresión logística en Python: Profundiza en cómo la regresión logística aprovecha el MLE para una clasificación eficaz y la estimación de parámetros.