Gaußsche Verteilung: Ein umfassender Leitfaden

Nur wenige Konzepte sind in der Statistik und Datenwissenschaft so grundlegend und weit verbreitet wie die Gauß-Verteilung. Dieses mathematische Modell, das auch als Normalverteilung bekannt ist, bildet die Grundlage für zahlreiche statistische Methoden und Datenanalysetechniken.

Dieses umfassende Handbuch erklärt das Konzept der Gaußschen Verteilungen und untersucht ihre Eigenschaften, Anwendungen und Bedeutung für die moderne Datenanalyse. Wir werden untersuchen, warum sie in der Natur so häufig vorkommen und wie sie in verschiedenen Bereichen eingesetzt werden, von der Finanzwelt bis zur Produktion.

Wenn du neu in der Statistik bist oder die Grundlagen auffrischen möchtest, bietet dir unser Kurs Einführung in die Statistik eine hervorragende Grundlage. Wenn du bereit bist, diese Konzepte in bestimmten Programmiersprachen anzuwenden, helfen dir unsere Kurse Statistical Thinking in Python (Teil 1) und Statistics Fundamentals with R dabei, die vielen Möglichkeiten zu verstehen, wie die Gauß-Verteilung in der deskriptiven und inferentiellen Statistik auftritt. 

Was ist eine Gaußsche Verteilung?

Die Gauß-Verteilung, die auch als Normalverteilung bezeichnet wird, ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die sich durch ihre glockenförmige Kurve auszeichnet. Sie wird durch zwei Parameter definiert:

1. μ (mu): Der Mittelwert oder Erwartungswert der Verteilung
2. σ (sigma): Die Standardabweichung, die die Streuung der Verteilung misst

Die Wahrscheinlichkeitsdichtefunktion (PDF) einer Gaußschen Verteilung ist gegeben durch:

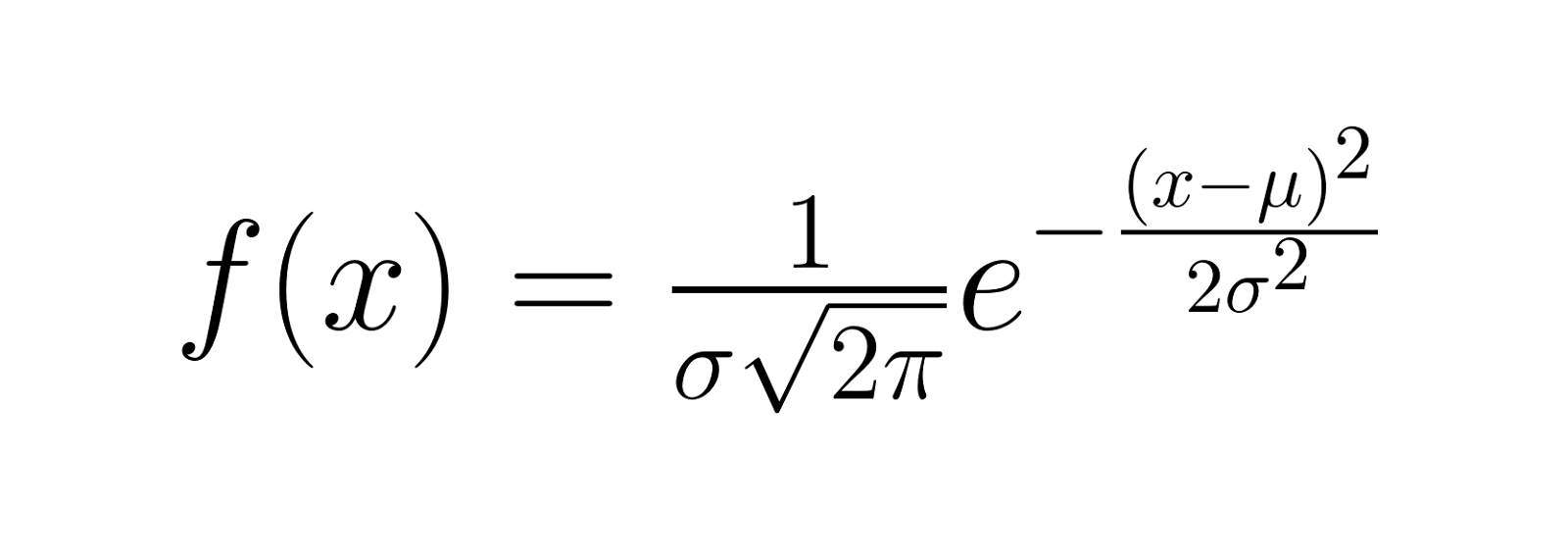
Wo:

• x ist die Variable
• e ist die Eulersche Zahl (ungefähr 2,71828)
• π (pi) ist die mathematische Konstante pi (ungefähr 3,14159)

Visualisierung der Gauß-Verteilung

Um das Konzept einer Gauß-Verteilung zu veranschaulichen, betrachte die Verteilung des Geburtsgewichts von Vollgeborenen in einer großen Population:

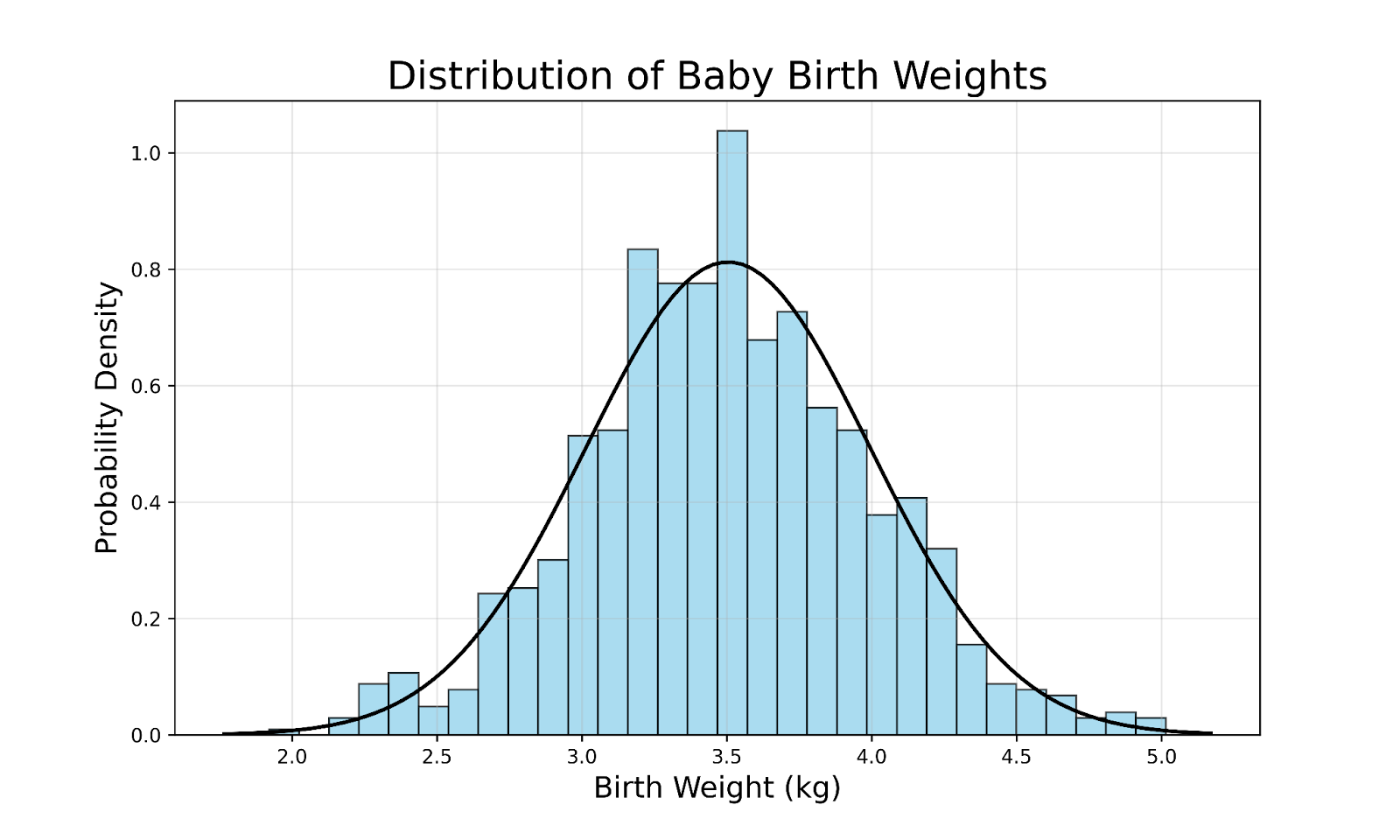
Einige wichtige Beobachtungen aus dieser Grafik sind:

• Das Geburtsgewicht der meisten Babys gruppiert sich um einen Durchschnittswert (die Spitze der Kurve).
• Weniger Babys haben ein Geburtsgewicht, das deutlich von diesem Durchschnitt abweicht.
• Nur sehr wenige Babys haben ein extremes Geburtsgewicht (sehr hoch oder sehr niedrig).

Das zentrale Grenzwertsatztheorem

Die weite Verbreitung von Gauß-Verteilungen in der Natur und in der Statistik lässt sich durch den zentralen Grenzwertsatz (CLT) erklären. Die CLT besagt, dass sich die Verteilung der Stichprobenmittelwerte mit zunehmender Stichprobengröße (z. B. n ≥ 30) einer Normalverteilung annähert, unabhängig von der Verteilung der Grundgesamtheit.

Ein wichtiger Aspekt der CLT ist, dass die Konvergenz zur Normalverteilung relativ schnell erfolgt, wenn der Stichprobenumfang zunimmt. Für die meisten praktischen Zwecke reichen schon mittelgroße Stichproben (z. B. n ≥ 30) aus, damit sich die Stichprobenmittelwerte einer Normalverteilung annähern. Das gilt auch dann, wenn die Bevölkerung selbst verzerrt ist.

Die Gaußsche Standardverteilung

Innerhalb der Klasse der Gauß-Verteilungen gibt es einen Spezialfall, der als Standard-Gauß-Verteilung bekannt ist, die auch als Standard-Normalverteilung bezeichnet wird. Dies ist eine Gaußsche Verteilung, bei der:

• Der Mittelwert (μ) ist genau 0.
• Die Standardabweichung (σ) ist genau 1.

Die Wahrscheinlichkeitsdichtefunktion einer Gaußschen Standardverteilung wird durch die folgende Formel beschrieben. 

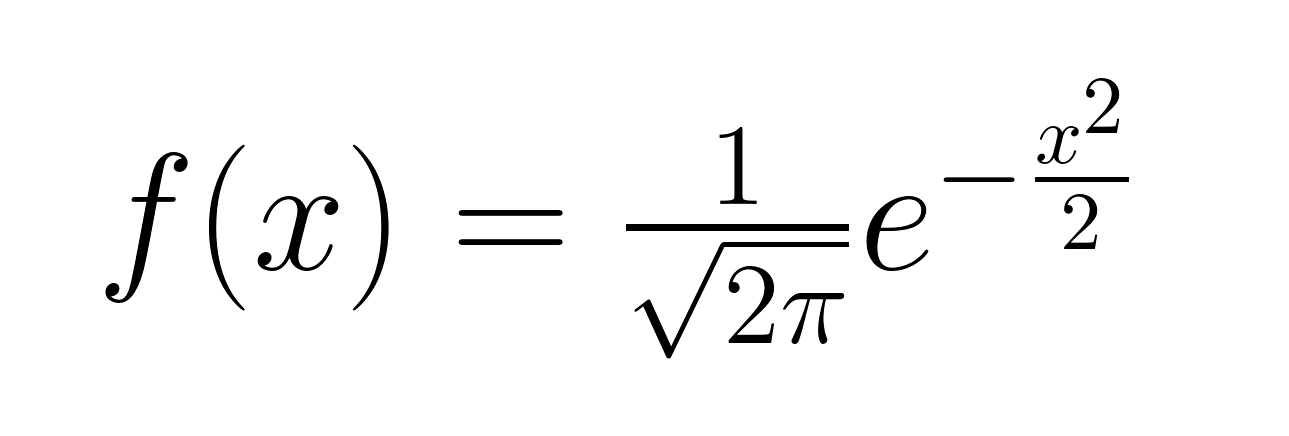
Beachte, dass die Formel für die Gaußsche Standard-Wahrscheinlichkeitsdichtefunktion aufgrund der spezifischen Werte, die dem Mittelwert und der Standardabweichung zugewiesen werden, einfacher ist als die allgemeine Form. Jetzt wollen wir uns die Gaußsche Standardverteilung ansehen.

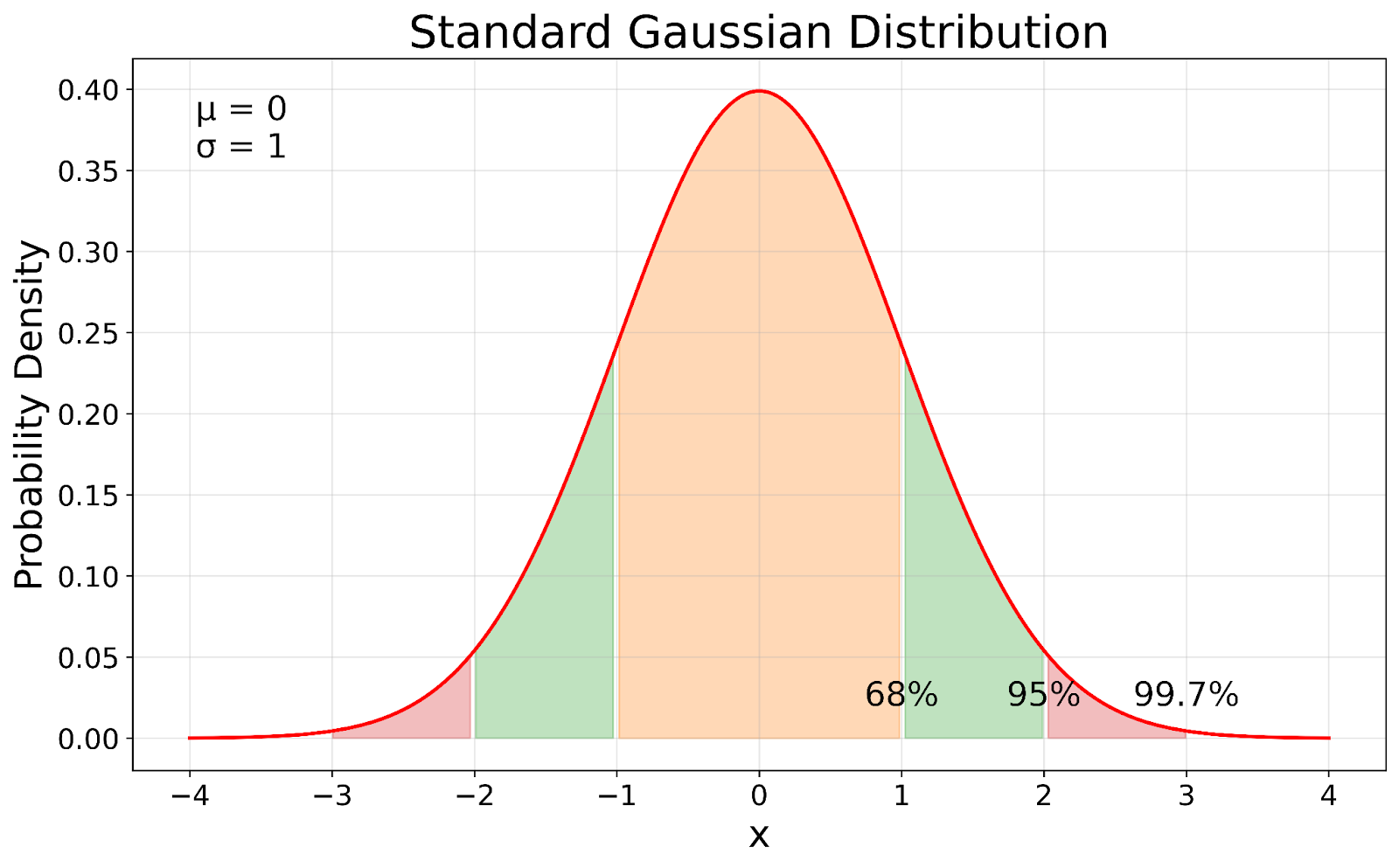Standard-Gauß-Verteilung. Bild vom Autor

Die Gaußsche Standardverteilung, die in unserer Visualisierung gezeigt wird, dient als Referenzpunkt in der Statistik. In unserer Grafik kannst du sehen, dass der Standard-Gauß eine standardisierte Version einer Gauß-Verteilung ist. Der Prozess der Standardisierung verschiebt den Mittelwert auf 0 und skaliert die Standardabweichung auf 1, wobei die grundlegenden Eigenschaften der Verteilung erhalten bleiben.

Eigenschaften von Gauß'schen Verteilungen

Schauen wir uns nun einige Eigenschaften der Gaußschen Verteilungen an.

Symmetrie und die Glockenkurve

Das Markenzeichen einer Gauß-Verteilung ist ihre symmetrische Glockenform. Diese Symmetrie bedeutet, dass die Daten mit gleicher Wahrscheinlichkeit über oder unter den Mittelwert fallen, was besonders nützlich ist, um Wahrscheinlichkeiten vorherzusagen und Rückschlüsse auf Daten zu ziehen. Wie die folgende Visualisierung zeigt, behalten alle Gaußverteilungen diese charakteristische Glockenform bei, unabhängig von ihrem Mittelwert oder ihrer Standardabweichung.

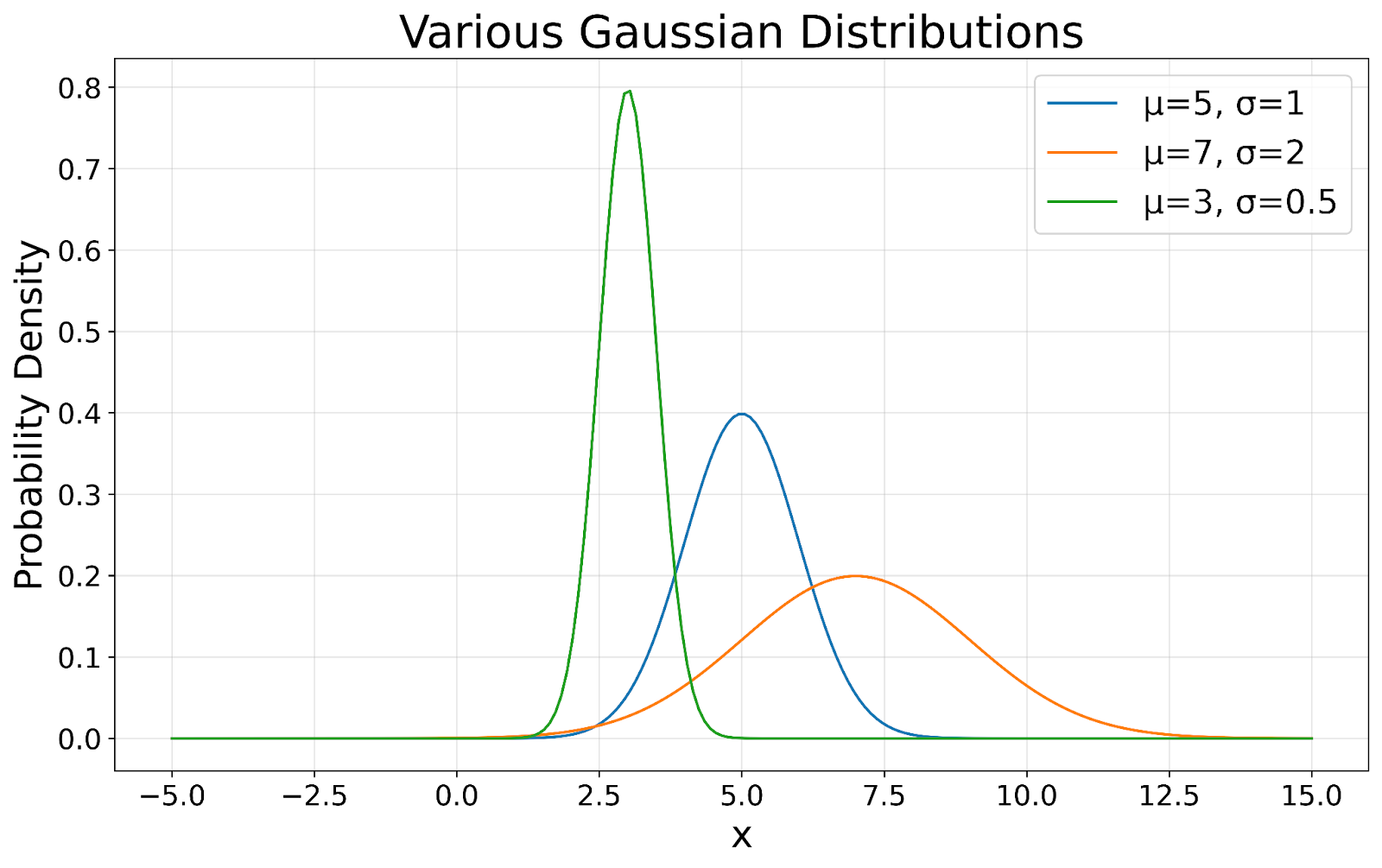Gaußverteilungen visualisiert. Bild vom Autor

Ausrichtung von Mittelwert, Median und Modus

Bei einer perfekten Gauß-Verteilung sind der Mittelwert (Durchschnitt), der Median (Mittelwert) und der Modus (häufigster Wert) alle gleich groß. Diese Ausrichtung gibt einen klaren Hinweis auf die zentrale Tendenz der Daten, was für die Zusammenfassung von Datensätzen wertvoll ist. In unserer Visualisierung kannst du sehen, wie die Spitze jeder Kurve diesen zentralen Punkt darstellt.

Standardabweichung und Datenverteilung

Die Standardabweichung einer Gauß-Verteilung sagt uns, wie weit die Daten vom Mittelwert entfernt sind. Sie folgt einem vorhersehbaren Muster:

• Etwa 68 % der Daten liegen innerhalb einer Standardabweichung vom Mittelwert.
• Etwa 95% liegen innerhalb von zwei Standardabweichungen.
• Etwa 99,7 % liegen innerhalb von drei Standardabweichungen.

Diese Regel, bekannt als die 68-95-99,7-Regelgilt für alle Gaußschen Verteilungen, unabhängig von ihrem Mittelwert oder ihrer Standardabweichung.

Praktische Anwendungen der Gaußschen Verteilungen

Gaußsche Verteilungen sind mehr als nur ein theoretisches Konzept - sie haben weitreichende Anwendungen in verschiedenen Bereichen. 

Statistische Inferenz und Hypothesentests

Viele statistische Tests, wie t-Tests und ANOVA, gehen davon aus, dass die Daten normal verteilt sind. Diese Tests helfen den Forschern festzustellen, ob es signifikante Unterschiede zwischen den Gruppen gibt oder ob die beobachteten Effekte wahrscheinlich auf Zufall zurückzuführen sind. Die Normalitätsannahme ermöglicht es den Forschern, p-Werte und Konfidenzintervalle zu berechnen und so einen Rahmen für Schlussfolgerungen aus den Daten und fundierte Entscheidungen zu schaffen. 

Die Normalitätsannahme ist so wichtig, dass Wiederholungsstichprobenverfahren wie das Bootstrapping entwickelt wurden, um aus nicht-normalen Daten normalverteilte Wiederholungsstichprobenverteilungen zu erzeugen, die die Konstruktion von Konfidenzintervallen und andere statistische Analysen erleichtern. Unser Tutorium über Hypothesentests zeigt, wie man diese Tests in verschiedenen Szenarien durchführt, einschließlich Situationen, in denen die Daten normal verteilt sind.

Algorithmen für maschinelles Lernen

Viele Verfahren des maschinellen Lernens beruhen auf der Annahme der Normalität, so dass Gaußverteilungen für ihre Funktionsweise und Interpretation grundlegend sind. Bei der linearen Regression wollen wir zum Beispiel sehen, dass die y-Werte (abhängige Variable) einer Normalverteilung folgen, um Vertrauen in unsere Schätzungen zu haben. Außerdem streben wir an, dass die Residuen (die Differenzen zwischen beobachteten und vorhergesagten Werten) eine Normalverteilung aufweisen. Diese Normalitätsannahmen liegen den statistischen Tests zugrunde, mit denen die Zuverlässigkeit des Modells und die Konfidenzintervalle für seine Vorhersagen bewertet werden.

Außerdem arbeiten Wissenschaftler/innen, die mit maschinellem Lernen arbeiten, aus Gründen der Recheneffizienz lieber mit Daten, die einer Gauß-Verteilung folgen. Eine Gauß-Verteilung kann bei bestimmten Algorithmen indirekt zur Recheneffizienz beitragen, insbesondere bei solchen, die eine Normalverteilung der Daten voraussetzen oder sich darauf verlassen.

• Effiziente Parameter-Schätzung: Bei einer Gauß-Verteilung sind der Mittelwert und die Varianz hinreichende Statistiken, d. h. sie beschreiben die Verteilung vollständig. Dies reduziert die Notwendigkeit einer komplexen Modellierung höherer Momente und beschleunigt die Parameterschätzung.
• Algorithmus Konvergenz: Algorithmen wie der Gradientenabstieg, die zur Optimierung beim maschinellen Lernen eingesetzt werden, konvergieren schneller, wenn die Daten normal verteilt sind. 
• Reduzierte Rechenkomplexität in einigen Algorithmen: Algorithmen wie Gaussian Naive Bayes sind speziell für normalverteilte Daten entwickelt worden und können rechnerisch effizient sein, wenn die Annahme zutrifft.